Online Walking Motion and Foothold Optimization for Quadruped Locomotion
Alexander W. Winkler Farbod Farshidian Michael Neunert Diego Pardo Jonas Buchli


IEEE Internation Conference on Robotics and Automation , 2017
www.awinkler.me
The Footholds' Primary Function is to Help the CoM move

A. Herdt et al, “Online Walking Motion Generation with Automatic Foot Step Placement,” HAL archives-ouvertes, 2010

Full-body To
Legged Locomotion MOdules
www.awinkler.me
Optimization Variables

www.awinkler.me
Unilateral Contact Forces
CoP inside Support-Area

M. Kalakrishnan et al, “Learning, planning, and control for quadruped locomotion over challenging terrain,” IJRR, 2010
www.awinkler.me
Unilateral Contact Forces
CoP inside Support-Area

M. Kalakrishnan et al, “Learning, planning, and control for quadruped locomotion over challenging terrain,” IJRR, 2010
www.awinkler.me


www.awinkler.me
How to Satisfy
?
Thanks!
www.awinkler.me
Simultaneous Footstep Planning
Nonlinear Constraint
1. Modify CoM motion \(\color{red}{\mathbf{a}}\) so that it can be generated by a CoP inside the current base of support.
2. Modify base of support by changing the footholds \(\color{red}{\mathbf{p}}\) to accommodate the CoM acceleration
www.awinkler.me
LIP Model to estimate Center-of-Pressure \(u\)
S. Kajita et al, “Biped walking pattern generation by using preview control of zero-moment point,” IEEE International Conference on Robotics and Automation, 2003.

www.awinkler.me
CoM Parametrization
Represent by sequence of fifth-order polynomials

Physical Feasiblity
An CoP at \(\mathbf{u}\) in state \(\mathbf{c}\) should cause a specific CoM acceleration.

www.awinkler.me





foothold
change
www.awinkler.me



foothold
change
www.awinkler.me
Range Of Motion COnstraint

www.awinkler.me
Tracking Optimized Motion

[1] F. Aghili, “A unified approach for inverse and direct dynamics of constrained multibody systems based on linear projection operator,” IEEE T-RO, 2005.
[2] M. Mistry, J. Buchli, and S. Schaal, “Inverse dynamics control of floating base systems using orthogonal decomposition,” IEEE ICRA, 2010
Cartesian \(\to\) Joint:
Joint+Contacts \(\to\) Torque \(^{[1,2]}\):
www.awinkler.me
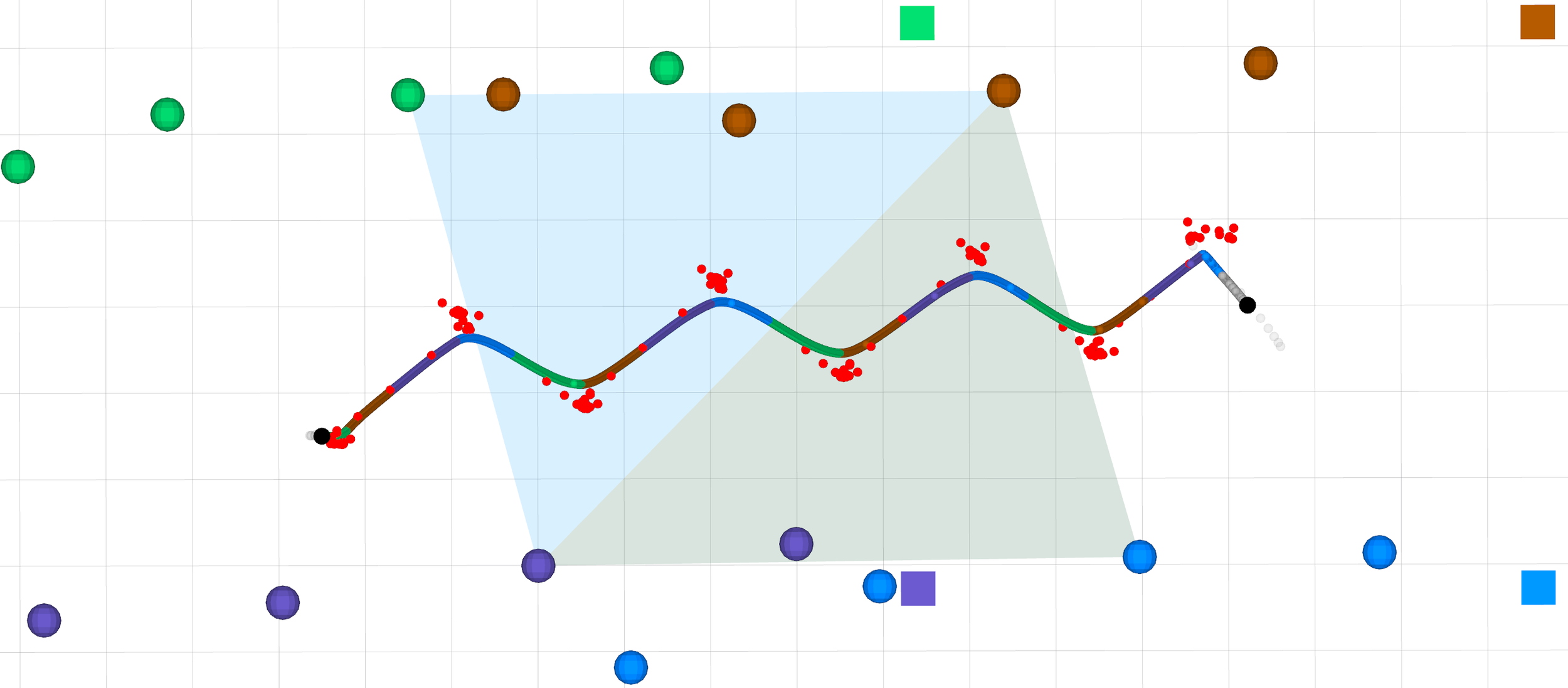
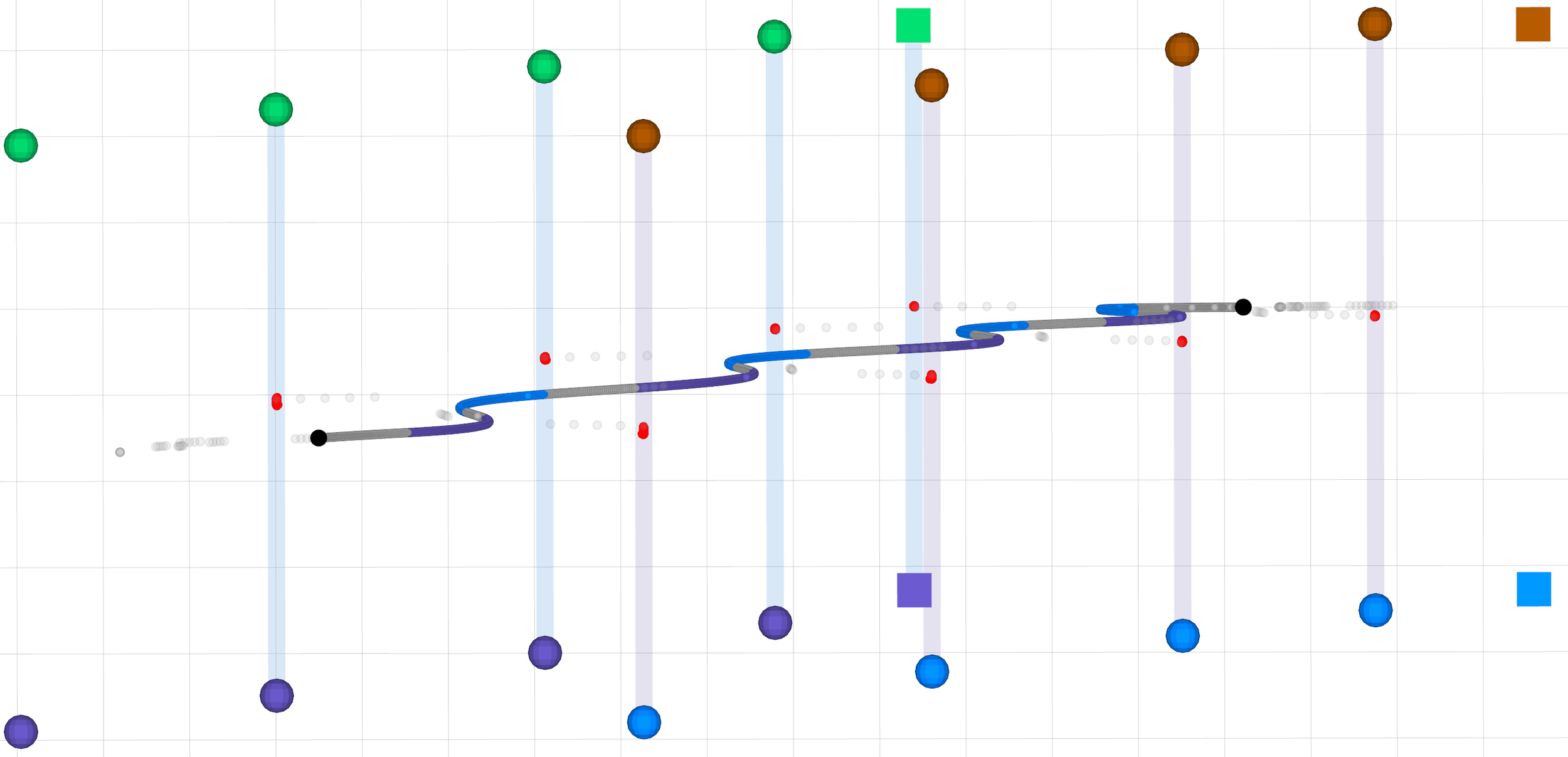
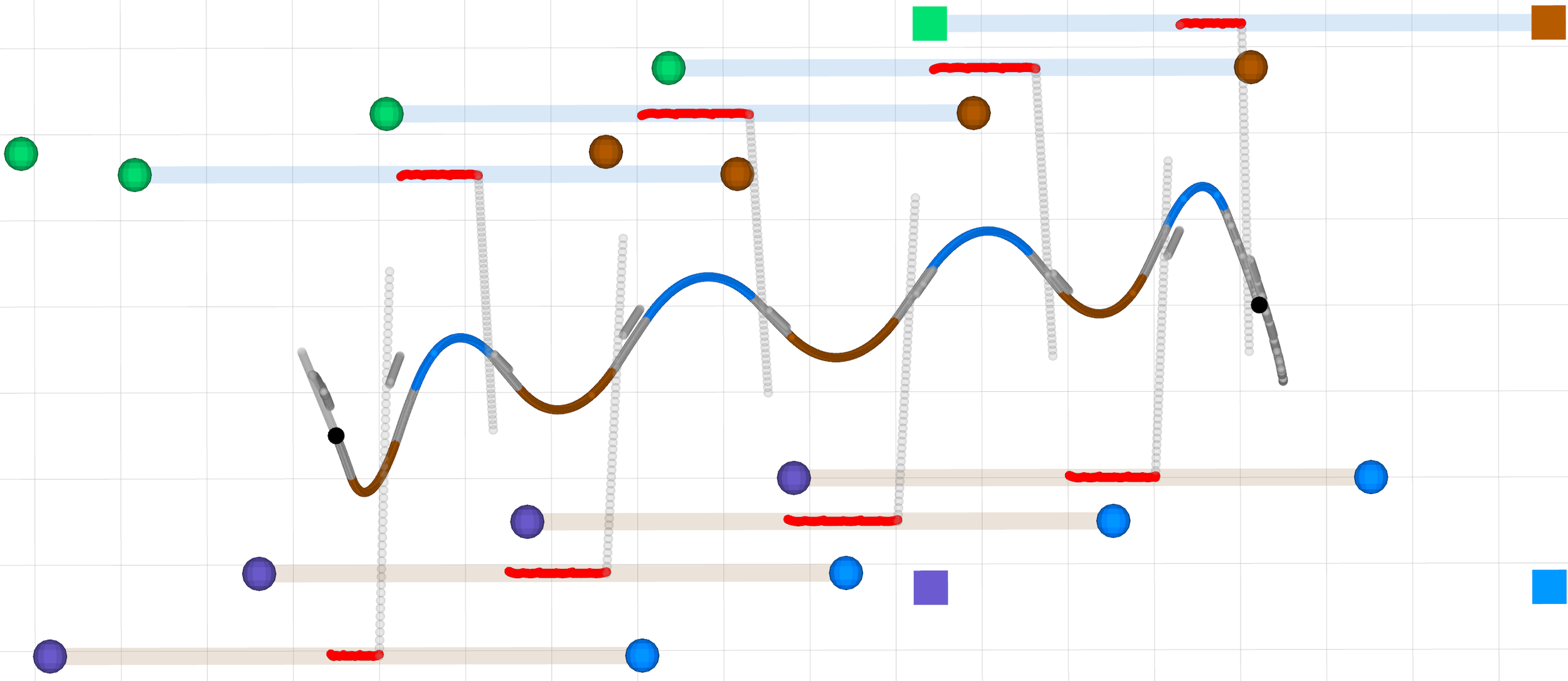
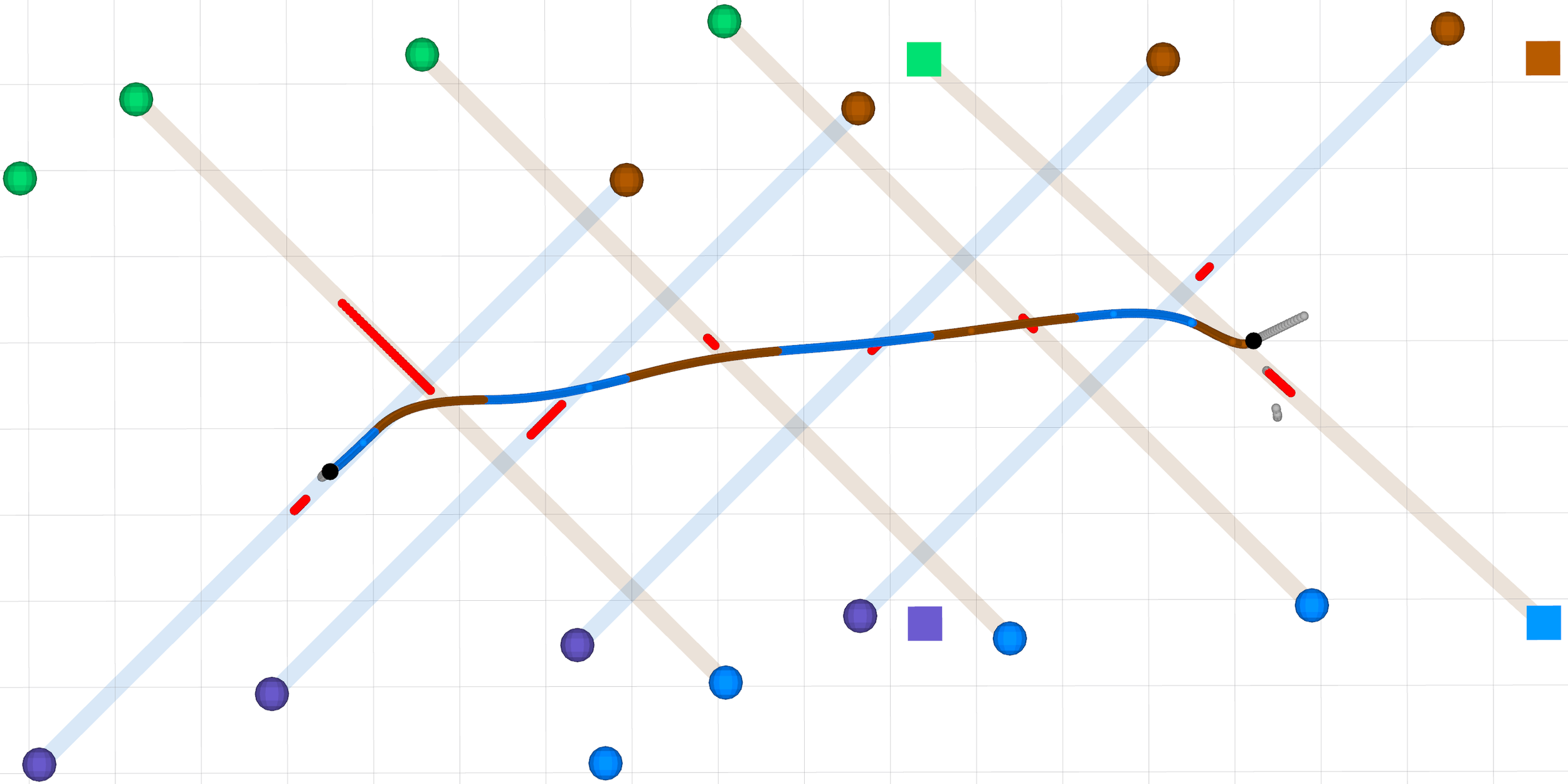
Walk
www.awinkler.me