Fast Trajectory Optimization for Legged Robots using Vertex-Based ZMP Constraints

Alexander W. Winkler
Farbod Farshidian
Diego Pardo
Michael Neunert
Jonas Buchli

Robot and Automation Letters (RA-L), 2017

(www.awinkler.me)

(ZMP)

(Capture Point)

Trotting

Push recovery

Walking

\mathbf{v}_0
v0\mathbf{v}_0

Pacing

Bounding

(Capture Point)

Single Formulation/Planner

Motivation

Alexander W. Winkler et al.

M. Kalakrishnan et al, “Learning, planning, and control for quadruped locomotion over challenging terrain,” IJRR, 2010

J. Pratt et al,  “Capture point: A step toward humanoid push recovery,” in Humanoids, 2006.

Single Formulation/Planner

Alexander W. Winkler et al.

M. Kalakrishnan et al, “Learning, planning, and control for quadruped locomotion over challenging terrain,” IJRR, 2010

J. Pratt et al,  “Capture point: A step toward humanoid push recovery,” in Humanoids, 2006.

Youtube: "animal gaits for animators"

Trajectory Optimization 

\text{find} \quad \color{black}{x(t)}, \color{black}{u(t)} , \quad \text{for } t \in [0,T]
findx(t),u(t),for t∈[0,T]\text{find} \quad \color{black}{x(t)}, \color{black}{u(t)} , \quad \text{for } t \in [0,T]
\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
subject tox(0)−x0=0\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
\dot{x} - f(x(t), u(t)) = 0
x˙−f(x(t),u(t))=0\dot{x} - f(x(t), u(t)) = 0
h(x(t), u(t)) \leq 0
h(x(t),u(t))≤0h(x(t), u(t)) \leq 0
x(T) - x_T = 0
x(T)−xT=0x(T) - x_T = 0
x(t), u(t) = \text{arg min } J(x,u)
x(t),u(t)=arg min J(x,u)x(t), u(t) = \text{arg min } J(x,u)

given initial state

dynamic Model

Path Constraints

Desired Final State

Objective

\text{find} \quad \color{red}{x(t)}, \color{red}{u(t)} , \quad \text{for } t \in [0,T]
findx(t),u(t),for t∈[0,T]\text{find} \quad \color{red}{x(t)}, \color{red}{u(t)} , \quad \text{for } t \in [0,T] 
Alexander W. Winkler et al.
\mathbf{c}(t)
c(t)\mathbf{c}(t)
\mathbf{u}(t)
u(t)\mathbf{u}(t)
\mathbf{p}_{3}
p3\mathbf{p}_{3}
\mathbf{p}_{4}
p4\mathbf{p}_{4}
\mathbf{p}_{2}
p2\mathbf{p}_{2}
\mathbf{p}_{1}
p1\mathbf{p}_{1}

OPtimization Variables

Alexander W. Winkler et al.

Dynamic Consistency

\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
findx(t),u(t),for t∈[0,T]\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
subject tox(0)−x0=0\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
\dot{x} - f(x(t), u(t)) = 0
x˙−f(x(t),u(t))=0\dot{x} - f(x(t), u(t)) = 0
h(x(t), u(t)) \leq 0
h(x(t),u(t))≤0h(x(t), u(t)) \leq 0
x(T) - x_T = 0
x(T)−xT=0x(T) - x_T = 0
x(t), u(t) = \text{arg min } J(x,u)
x(t),u(t)=arg min J(x,u)x(t), u(t) = \text{arg min } J(x,u)

Linear Inverted Pendulum Model

S. Kajita et al, “Biped walking pattern generation by using preview control of zero-moment point,” IEEE International Conference on Robotics and Automation, 2003.

\ddot{\mathbf{c}}(t) = \frac{g}{h}(\mathbf{c}(t)- \color{red}{\mathbf{u}}(t))
c¨(t)=gh(c(t)−u(t)) \ddot{\mathbf{c}}(t) = \frac{g}{h}(\mathbf{c}(t)- \color{red}{\mathbf{u}}(t))
Alexander W. Winkler et al.

foothold

change

Alexander W. Winkler et al.

Simultaneous Base and Feet Optimization

Unilateral Contact Forces 

\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
findx(t),u(t),for t∈[0,T]\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
subject tox(0)−x0=0\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
\dot{x} - f(x(t), u(t)) = 0
x˙−f(x(t),u(t))=0\dot{x} - f(x(t), u(t)) = 0
h(x(t), u(t)) \leq 0
h(x(t),u(t))≤0h(x(t), u(t)) \leq 0
x(T) - x_T = 0
x(T)−xT=0x(T) - x_T = 0
x(t), u(t) = \text{arg min } J(x,u)
x(t),u(t)=arg min J(x,u)x(t), u(t) = \text{arg min } J(x,u)
\color{green}{\mathbf{c}} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}
c=[1110]\color{green}{\mathbf{c}} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}
\color{green}{\mathbf{c}} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix}
c=[0110]\color{green}{\mathbf{c}} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix}
u
uu
u
uu
\color{red}{\mathbf{u}}^T \mathbf{n}_i(\mathbf{p}) + \text{offset}(\mathbf{p}) > 0
uTni(p)+offset(p)>0\color{red}{\mathbf{u}}^T \mathbf{n}_i(\mathbf{p}) + \text{offset}(\mathbf{p}) > 0

Unilateral Contact Forces           CoP inside Support-Area 

\Leftrightarrow
⇔\Leftrightarrow

M. Kalakrishnan et al, “Learning, planning, and control for quadruped locomotion over challenging terrain,” IJRR, 2010

Alexander W. Winkler et al.
  • Cannot represent single point-contacts or lines  
    • Heuristic expansion of points or lines into areas
  • Ordering of contact points necessary.
\color{red}{\mathbf{u}} = \sum\limits_{i=1}^4 \lambda_i \mathbf{p}_i
u=∑i=14λipi\color{red}{\mathbf{u}} = \sum\limits_{i=1}^4 \lambda_i \mathbf{p}_i
\sum\limits_{i=1}^{4} \lambda_i = 1
∑i=14λi=1\sum\limits_{i=1}^{4} \lambda_i = 1
0 < \lambda_i
0<λi0 < \lambda_i
\color{green}{\mathbf{c}} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}
c=[1110]\color{green}{\mathbf{c}} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}
\color{green}{\mathbf{c}} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix}
c=[0110]\color{green}{\mathbf{c}} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix}
< c_i
<ci< c_i
u
uu
u
uu

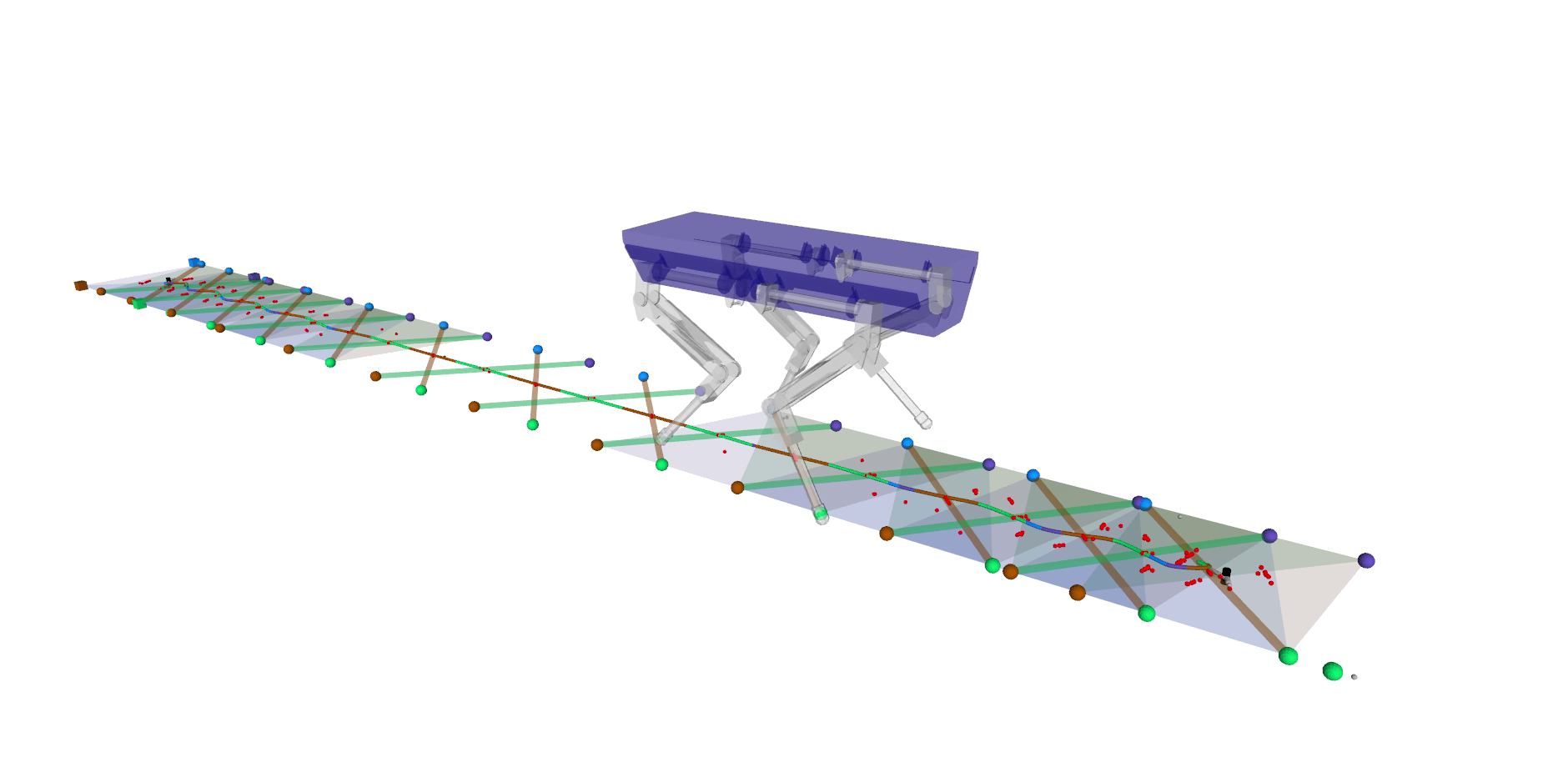
Vertex-Based Zmp-Constraint Formulation 

Alexander W. Winkler et al.

Future Work

(under review for ICRA/RAL 2018)

F. Farshidian

D. Pardo

M. Neunert

J. Buchli

A. Winkler

Paper, Video and Presentation: www.awinkler.me

  • Reduce heuristics  by simultaneously optimizing over body motion and footholds

  • Vertex-based ZMP-constraint formulation allows to uniformly handle point-, line- and area-contacts

Take-Away MSGs

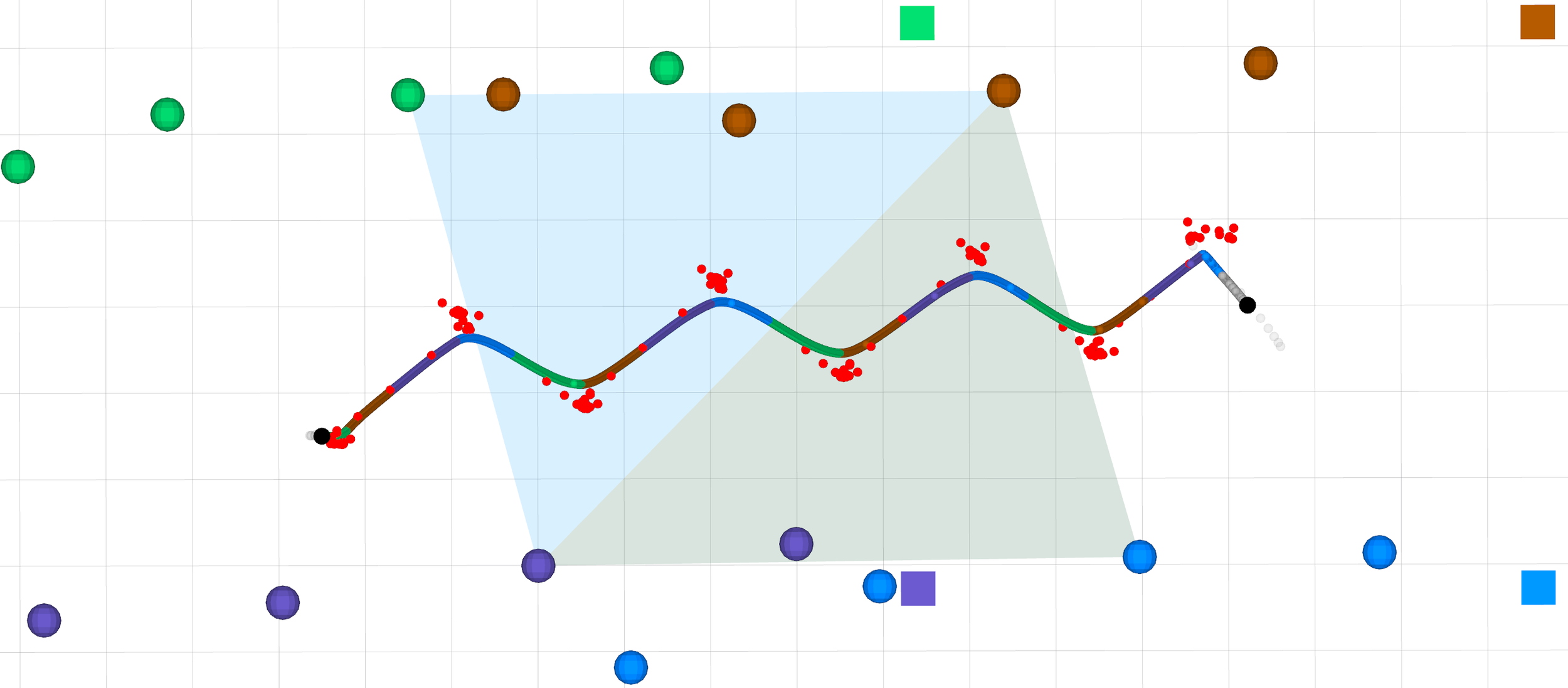
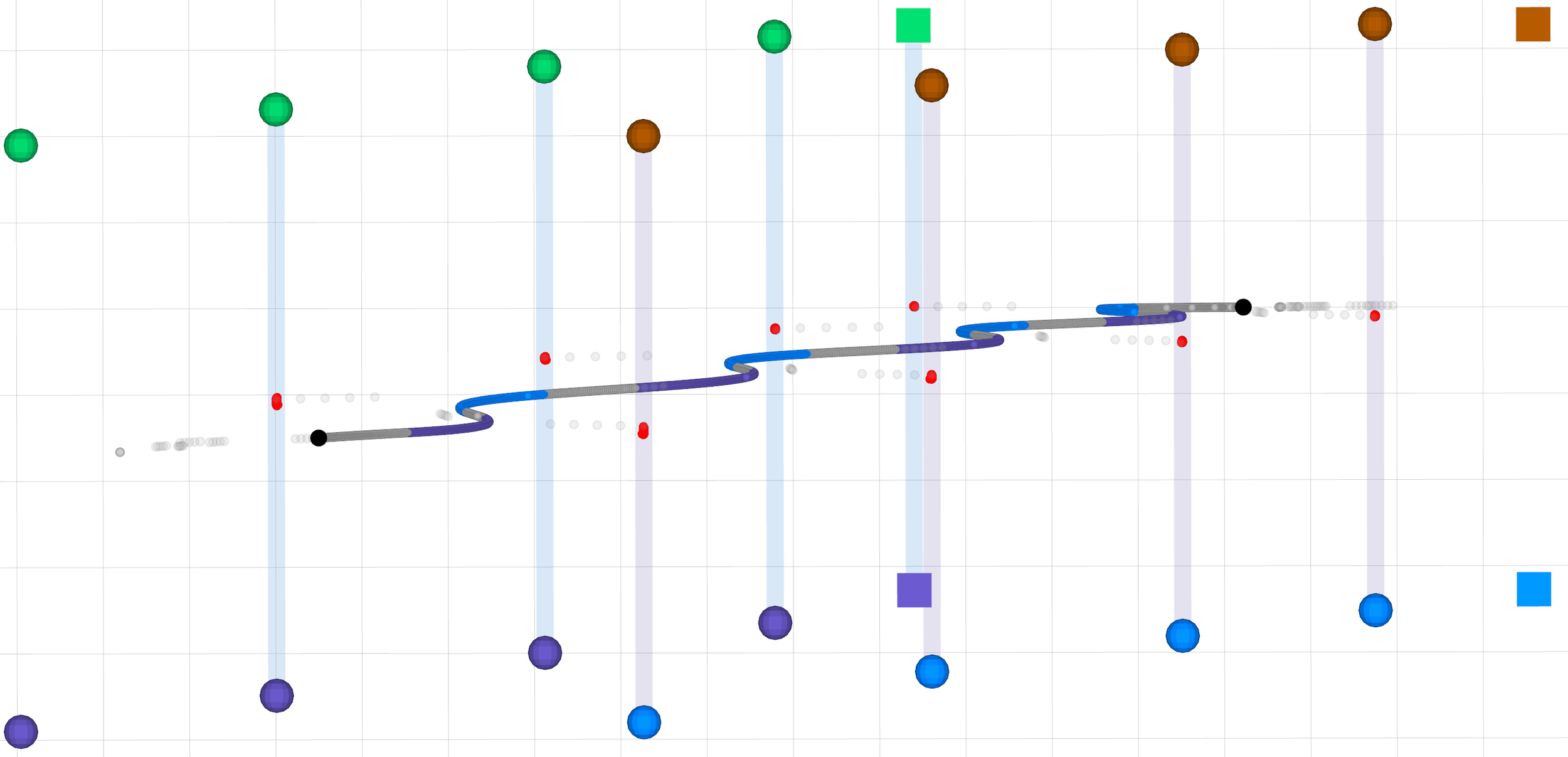
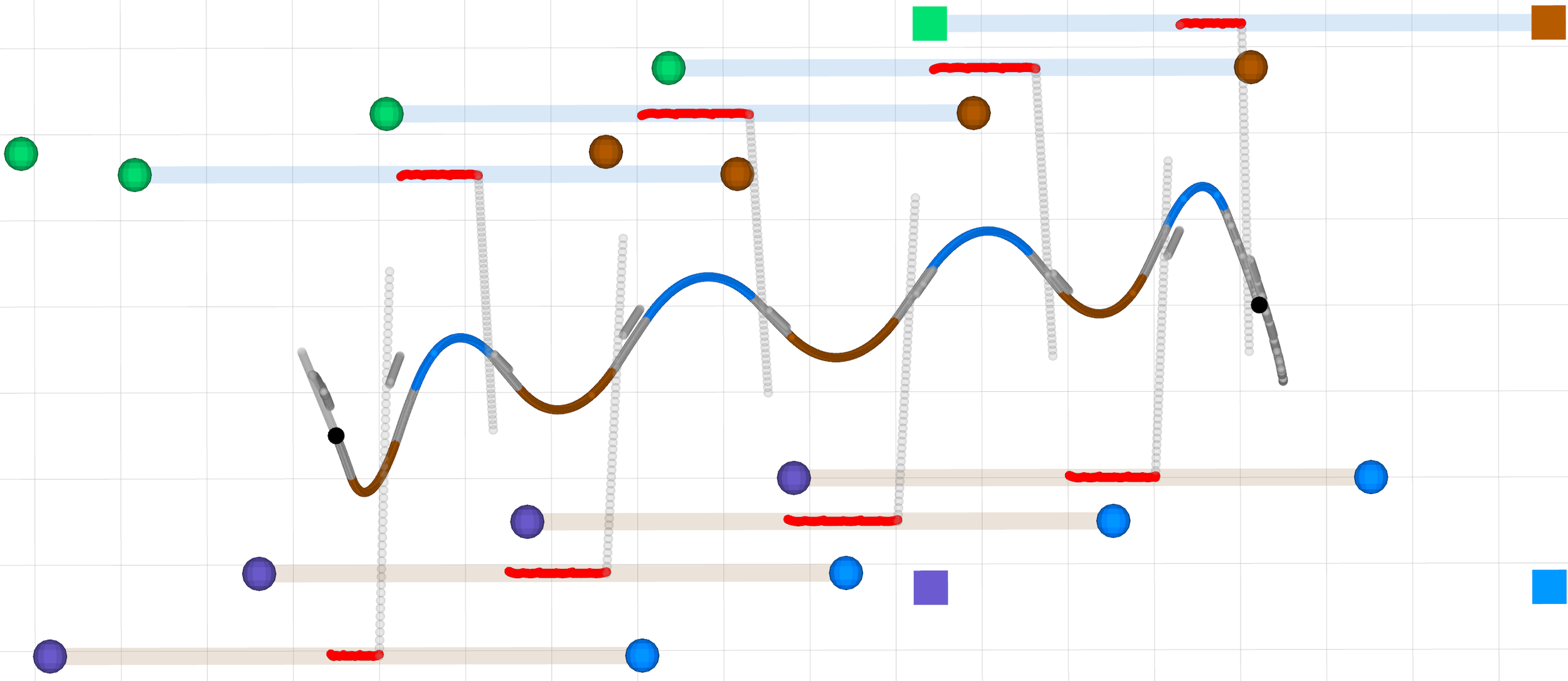
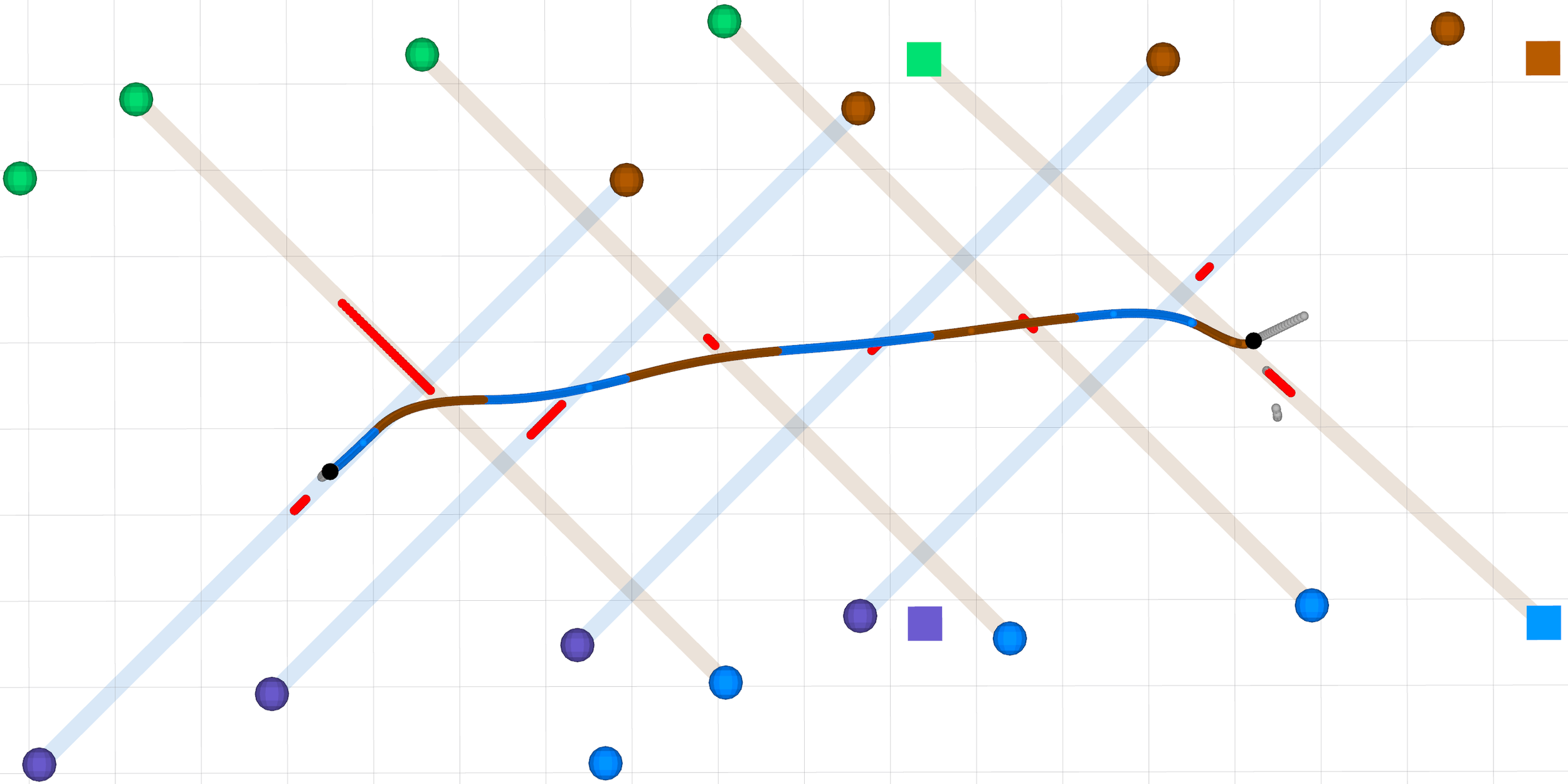
Walk

Trot

Bound

Pace

Alexander W. Winkler et al.

Kinematic Range

\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
findx(t),u(t),for t∈[0,T]\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
subject tox(0)−x0=0\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
\dot{x} - f(x(t), u(t)) = 0
x˙−f(x(t),u(t))=0\dot{x} - f(x(t), u(t)) = 0
h(x(t), u(t)) \leq 0
h(x(t),u(t))≤0h(x(t), u(t)) \leq 0
x(T) - x_T = 0
x(T)−xT=0x(T) - x_T = 0
x(t), u(t) = \text{arg min } J(x,u)
x(t),u(t)=arg min J(x,u)x(t), u(t) = \text{arg min } J(x,u)

kinematic Range:

\mathbf{p}_{i=1..4} \in \mathcal{R}(\mathbf{c})
pi=1..4∈R(c)\mathbf{p}_{i=1..4} \in \mathcal{R}(\mathbf{c})
\mathbf{p}_{LF}
pLF\mathbf{p}_{LF}
\mathcal{R}_{LF}
RLF\mathcal{R}_{LF}
\mathcal{R}_{RF}
RRF\mathcal{R}_{RF}
\mathcal{R}_{RH}
RRH\mathcal{R}_{RH}
\mathcal{R}_{LH}
RLH\mathcal{R}_{LH}
\mathbf{c}
c\mathbf{c}
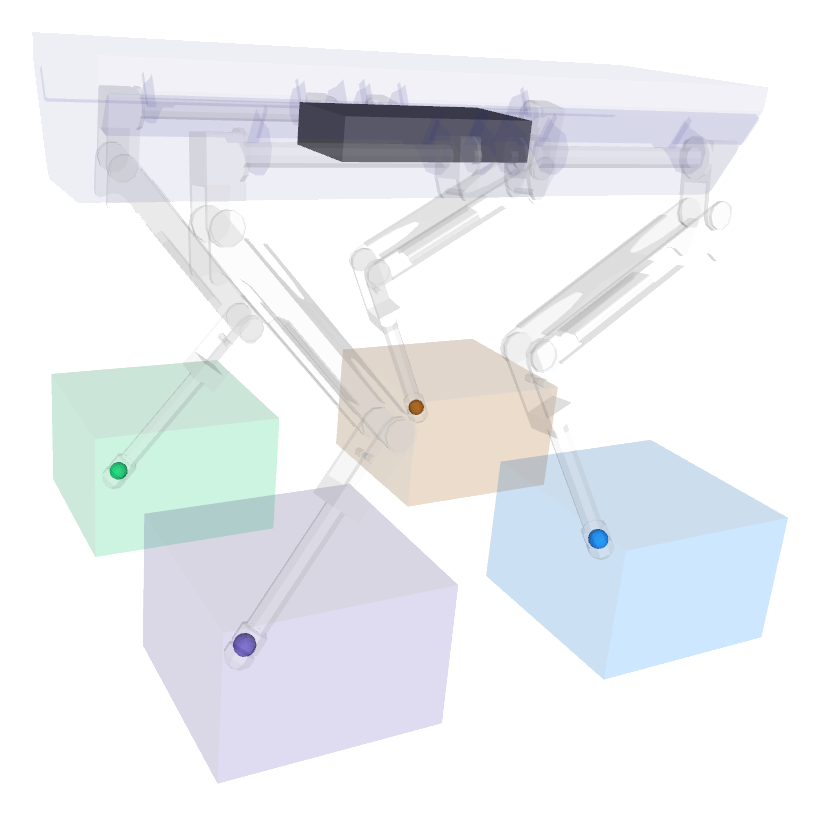
Alexander W. Winkler et al.

Robust Motions

\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
findx(t),u(t),for t∈[0,T]\text{find} \quad x(t), u(t) , \quad \text{for } t \in [0,T]
\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
subject tox(0)−x0=0\text{subject to} \quad \mathbf{x}(0) - \mathbf{x}_0 = 0
\dot{x} - f(x(t), u(t)) = 0
x˙−f(x(t),u(t))=0\dot{x} - f(x(t), u(t)) = 0
h(x(t), u(t)) \leq 0
h(x(t),u(t))≤0h(x(t), u(t)) \leq 0
x(T) - x_T = 0
x(T)−xT=0x(T) - x_T = 0
x(t), u(t) = \text{arg min } J(x,u)
x(t),u(t)=arg min J(x,u)x(t), u(t) = \text{arg min } J(x,u)
\mathbf{u}
u\mathbf{u}
\mathbf{\lambda} = \begin{bmatrix} 0 \\ 0.5 \\ 0.5 \\ 0 \end{bmatrix}
λ=[00.50.50]\mathbf{\lambda} = \begin{bmatrix} 0 \\ 0.5 \\ 0.5 \\ 0 \end{bmatrix}
\mathbf{\lambda}^* = \begin{bmatrix} 0.33 \\ 0.33 \\ 0.33 \\ 0 \end{bmatrix}
λ∗=[0.330.330.330]\mathbf{\lambda}^* = \begin{bmatrix} 0.33 \\ 0.33 \\ 0.33 \\ 0 \end{bmatrix}
J = \sum\limits_{k=1}^{n} |\!| \mathbf{\lambda}_k - \mathbf{\lambda}_k^* |\!|_2^2
J=∑k=1n∣∣λk−λk∗∣∣22J = \sum\limits_{k=1}^{n} |\!| \mathbf{\lambda}_k - \mathbf{\lambda}_k^* |\!|_2^2
\mathbf{u}^*
u∗\mathbf{u}^*

"If possible, Avoid The Extremes"

Alexander W. Winkler et al.
\mathbf{u} \in \mathcal{P}(\mathbf{p},c)
u∈P(p,c)\mathbf{u} \in \mathcal{P}(\mathbf{p},c)
\color{red}{\mathbf{u}} = \sum\limits_{i=1}^8 \lambda_i \mathbf{v}_i(\mathbf{p},\alpha)
u=∑i=18λivi(p,α)\color{red}{\mathbf{u}} = \sum\limits_{i=1}^8 \lambda_i \mathbf{v}_i(\mathbf{p},\alpha)
\sum\limits_{i=1}^{8} \lambda_i = 1
∑i=18λi=1\sum\limits_{i=1}^{8} \lambda_i = 1
\Leftrightarrow
⇔\Leftrightarrow
0 < \lambda_i
0<λi0 < \lambda_i

Biped with non-point-feet:

\mathbf{c} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}
c=[11111111]\mathbf{c} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}
< c_i
<ci< c_i

Generating Torques to Track the Optimized Motion

\Leftrightarrow \ddot{\mathbf{q}}_{j,ref} = \mathbf{J}_j^+ ( \color{red}{\ddot{\mathbf{p}}} - \dot{\mathbf{J}}\dot{\mathbf{q}} - \mathbf{J}_b \color{red}{\ddot{\mathbf{q}}_{b,ref}} )
⇔q¨j,ref=Jj+(p¨−J˙q˙−Jbq¨b,ref)\Leftrightarrow \ddot{\mathbf{q}}_{j,ref} = \mathbf{J}_j^+ ( \color{red}{\ddot{\mathbf{p}}} - \dot{\mathbf{J}}\dot{\mathbf{q}} - \mathbf{J}_b \color{red}{\ddot{\mathbf{q}}_{b,ref}} )
\ddot{\mathbf{p}} = \mathbf{J} \ddot{\mathbf{q}} + \dot{\mathbf{J}} \dot{\mathbf{q}}
p¨=Jq¨+J˙q˙\ddot{\mathbf{p}} = \mathbf{J} \ddot{\mathbf{q}} + \dot{\mathbf{J}} \dot{\mathbf{q}}
\mathbf{P} = \mathbf{I} - \mathbf{J}_c^+ \mathbf{J}_c
P=I−Jc+Jc\mathbf{P} = \mathbf{I} - \mathbf{J}_c^+ \mathbf{J}_c
\mathbf{\tau} = (\mathbf{P} \mathbf{S}^T)^+ \mathbf{P} ( \mathbf{M}\ddot{\mathbf{q}}_{ref} + \mathbf{C} )
τ=(PST)+P(Mq¨ref+C)\mathbf{\tau} = (\mathbf{P} \mathbf{S}^T)^+ \mathbf{P} ( \mathbf{M}\ddot{\mathbf{q}}_{ref} + \mathbf{C} )

[1] F. Aghili, “A unified approach for inverse and direct dynamics of constrained multibody systems based on linear projection operator: Applications to control and simulation,” IEEE T-RO, 2005.

[2] M. Mistry, J. Buchli, and S. Schaal, “Inverse dynamics control of floating base systems using orthogonal decomposition,” IEEE ICRA, 2010

Cartesian \(\to\) Joint:

Joint+Contacts \(\to\) Torque \(^{[1,2]}\): 

Made with Slides.com