Madrid - April, 2017

Historical Development of Algebraic Geometry

J. DIEUDONNÉ, interpreted by @hannelita

Who are you?

Hi! I'm Hanneli (@hannelita)

  • Computer Engineer
  • Programming
  • Electronics
  • Math <3 <3
  • Physics
  • Lego
  • Meetups
  • Animals
  • Coffee
  • Pokémon
  • GIFs

Olá! I'm Hanneli (@hannelita)

  • Computer Engineer
  • Programming
  • Electronics
  • Math <3 <3
  • Physics
  • Lego
  • Meetups
  • Animals
  • Coffee
  • Pokémon
  • GIFs

This is my first time at PWL! :)

Who is this author?

  • Jean Dieudonné - 1906 -1992
  • Your neighbour (French)
  • He taught in France, in the USA and also in Brazil!
  • Research in abstract algebra, algebraic geometry and functional analysis

Why this paper?

Algebraic

Geometry

2 + 2 = 4
2+2=42 + 2 = 4

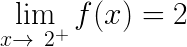
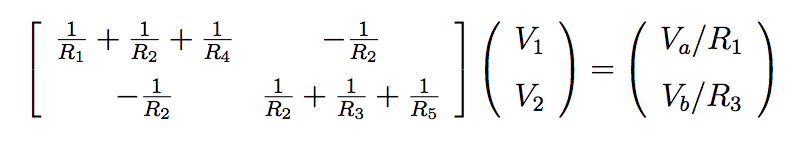
What is the relation between curves and programming?

  • Computer vision / Computer Graphics
  • Linear/non-linear programming (geometric solutions)

Computational

Geometry

GIS, computer vision, computer-aided engineering, Integrated-circuit design

Am I missing something?

What is the relation between geometry and programming?

  • Computer vision / Computer Graphics
  • Linear/non-linear programming (geometric solutions)
  • Algorithm complexity
  • Elliptic curve cryptography

I was

According to Wikipedia:

And now, finally, the

Historical Development of Algebraic Geometry

The structure of this paper

and presentation

a. Mention something that happened in history

b. Associate with a field in Mathematics

c. Come up with interesting relations

Disclaimer

I don't understand 100% of the definitions on this paper :')

We won't cover every detail on this extensive study

No formalism - sorry! Simplicity.

Goals

Better connection between maths - programming

New fields for research

How are these pieces connected?

Too many fields, too many theorems

"Algebraic geometry has more open problems than solved ones"

Algebraic Geometry

Classification

Transformation

Infinitely

near points

Extending the Scalars

Extending the space

Analysis and Topology

Commutative Algebra

1. The Greeks (The Geometry folks)

Geometry to solve algebraic problems

Apollonius studies conics

Beginning of analytic geometry

~630 BC

2. Analytic Geometry

1630 - 1795

Descartes, Fermat, Newton, Leibniz

Parametric representations, surfaces, coordinates

2. Analytic Geometry

1630 - 1795

Descartes, Fermat, Newton, Leibniz

Parametric representations, surfaces, coordinates

Classification

Transformation

Infinitely

near points

2. Analytic Geometry

1630 - 1795

Descartes, Fermat, Newton, Leibniz

Parametric representations, surfaces, coordinates

Classification

Transformation

Infinitely

near points

Theory of Determinants

3. Projective Geometry

1795 - 1850

Development of conics and quadrics (FINALLY!)

3. Projective Geometry

1795 - 1850

Development of conics and quadrics (FINALLY!)

Extending the Scalars

Extending the space

3. Projective Geometry

1795 - 1850

Development of conics and quadrics (FINALLY!)

Extending the Scalars

Extending the space

Complex points

n-dimensional spaces

3. Projective Geometry

1795 - 1850

Klein

Geometry and Group Theory (Galois)

WHAT IS GROUP THEORY?

3.1 Group theory made simple

"Group Theory tries to collect patterns in mathematical objects and put them in such way that we can analyse symmetries"

TAVANTE, H. 2016 (me)

https://medium.com/@hannelita/a-summary-of-topics-in-mathematics-ff573e520986

3.1 Group theory made simple

If I take this object, what happens if I rotate it clockwise? Is there any other element with the same behaviour?

Group theory helps you to detect patterns.

If I make some transformations on this object, it will be identical to another structure

3.1 Group theory made simple

If I take this object, what happens if I rotate it clockwise? Is there any other element with the same behaviour?

Group theory helps you to detect patterns.

If I make some transformations on this object, it will be identical to another structure

Transformation

3.2 Towards projective geometry

Forget the distance. This about the configuration of the points and lines. The metric doesn't matter.

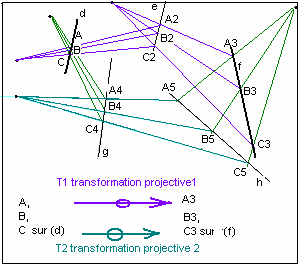
Desargues, Poncelet

4. Birrational Geometry

1850 - 1866

Riemann

"... transcendental approach via abelian integrals was important to algebraic geometry"

4. Birrational Geometry

1850 - 1866

Riemann

"... transcendental approach via abelian integrals was important to algebraic geometry"

4.1 Abel

Me: "I don't understand the meaning of 'abelian integral' "

4.1 Abel

Abelian integral

f(z,w) = z + (3w^2 - w + 2) = 0
f(z,w)=z+(3w2−w+2)=0f(z,w) = z + (3w^2 - w + 2) = 0
\int_{0}^{1} \frac{z}{w} dz
∫01zwdz\int_{0}^{1} \frac{z}{w} dz
w(z) = \frac{1}{6(1 + \sqrt{23 - 12z})}
w(z)=16(1+23−12z)w(z) = \frac{1}{6(1 + \sqrt{23 - 12z})}
\int_{0}^{1}\frac{z}{\frac{1}{6(1 + \sqrt{23 - 12z})}} dz
∫01z16(1+23−12z)dz\int_{0}^{1}\frac{z}{\frac{1}{6(1 + \sqrt{23 - 12z})}} dz

4.1 Abel

Why is it important?

Multi-valued expression that is easy to manipulate! 

Multi-valued expressions can denote surfaces

Riemann comes in! Using Abel ideas, he changes the initial object

4.2 Back to group theory

Function with this property

Holomorphic

(Complex function differentiable in every point of its domain)

Except on single "peaks"(poles)

Meromorphic

Function

4.2 Riemann's idea

Function with this property

Holomorphic

(Complex function differentiable in every point of its domain)

Except on single "peaks"(poles)

Meromorphic

Function

(Ex: Gamma function ^)

Random question: Given two functions, are they isomorphic (map one to another)? 

How can I compare them in different spaces?

Take Abel's rational functions idea - Birrational geometry

The object is always a rational

4.2 Riemann's idea

Riemann notices some invariants on these functions (genus)

4.2 Riemann's idea

Classification

Break - Breathe!

5. Development and Chaos

1866 - 1920

Riemann inserted several ideas for algebraic geometry. Different schools tried to extend them with different approaches

4 different attempts:

5. Development and Chaos

1866 - 1920

a) The algebraic approach - Kronecher, Dedeking and Weber

Algebraic geometry and Number theory

5. Development and Chaos

1866 - 1920

a) The algebraic approach - Kronecher, Dedeking and Weber

Algebraic geometry and Number theory

"adding and product of integers (module a prime number) has
the algebraic structure of a finite field" - credits by Luis L., attendee

5. Development and Chaos

1866 - 1920

a) The algebraic approach - Kronecher, Dedeking and Weber

Algebraic geometry and Number theory

Commutative Algebra

5. Development and Chaos

1866 - 1920

a) The algebraic approach - Kronecher, Dedeking and Weber

Algebraic geometry and Number theory

Commutative Algebra

(Study of objects where the multiplication is commutative)

5. Development and Chaos

1866 - 1920

a) The algebraic approach - Kronecher, Dedeking and Weber

Algebraic geometry and Number theory

Commutative Algebra

(call these objects 'rings')

5. Development and Chaos

1866 - 1920

a) The algebraic approach - Kronecher, Dedeking and Weber

Algebraic geometry and Number theory

Commutative Algebra

*What is a non-example of commutative ring?*

5. Development and Chaos

Why is commutative algebra important?

Statistics and combinatory - think about ML and AI

a) Algebraic geometry and Number theory

5. Development and Chaos

M. Noether and Brill

b) Theory of linear systems of points of a curve

Infinitely

near points

Extending the space

No rational functions - any polynomials.

Quadratic transformations

5. Development and Chaos

Cayley, Clebsch and Noether

c) Integrals of differential forms on higher dimensional varieties

Back to rational functions (ROLLBACK!)

5. Development and Chaos

Cayley, Clebsch and Noether

c) Integrals of differential forms on higher dimensional varieties

Back to rational functions (ROLLBACK!)

Analysis and Topology

Infinitely

near points

5. Development and Chaos

c) Integrals of differential forms on higher dimensional varieties

What would it be a good invariant to observe in a surface?

"Number of holes"

How do you measure that in an n-dimensional scenario?

5. Development and Chaos

c) Integrals of differential forms on higher dimensional varieties

Betti number: "number of k-dimensional holes on a topological surface"

By H. Poincaré

Consider the Betti number on further analysis

5. Development and Chaos

d) Linear systems and the Italian School

Castelnuovo, Enriques and Severi

Claim: "Purely geometric", no "abstract"

Limitations to some transformations

5. Development and Chaos

d) Linear systems and the Italian School

Castelnuovo, Enriques and Severi

Claim: "Purely geometric", no "abstract"

Limitations to some transformations

Classification

6. New Structures

1920 - 1950

Unification of mathematics through structures

Manifold

"some space such that if you zoom in, it looks like flat euclidean space."

4 New approaches for algebraic geometry (we will see 2 cases)

6. New Structures

a) Kahlerian varieties

Differential

Geometry

Riemann geometry (curved surfaces) + Calculus

6. New Structures

b) Abstract Algebraic Geometries

Commutative Algebra

Notion of abstract struct (ring, group, field) is solid

Noether, Krull, van de Waerden and F.K. Schmidt

6. New Structures

b) Abstract Algebraic Geometries

Commutative Algebra

Ring on an Ascending Chain Condition (ex: the field of Rational numbers is a Noetherian ring)

Noether, Krull, van de Waerden and F.K. Schmidt

BREAK!

It reveals surprising connections

Why are we studying these topics?

It is fun (???)

History

"Unentangle" - "Unfortunately, the complexity of the Italian definitions was such that it was often impossible to be sure that the same words meant the same thing in two different papers"

BREAK!

We don't know!

Where are we going?

But look! Now geometry is "abstract", "complex", it has algebra, invariants, transformations and several other components far from those we learn in High School

6. New Structures

c) Bonus: Zeta Functions and correspondences

A. Weil

6. New Structures

c) Zeta Functions and correspondences

A. Weil

Infinitely

near points

Extending the Scalars

\zeta(s) = \sum_{1}^{\infty}\frac{1}{n^s}
ζ(s)=∑1∞1ns\zeta(s) = \sum_{1}^{\infty}\frac{1}{n^s}

7. Sheaves and Schemes

1950 - now

Sheaf

"A tool which provides a unified approach

to establishing connections between local

and global properties of topological

spaces"

(topological space: space of points and their neighbourhoods satisfying properties)

2 cents: mathematicians have several names for groups of things that follow the same principles

7. Sheaves

Associate algebraic objects with other distinct mathematical objects is the study of homology

You can map different types of objects.

commutative group

(abelian group)

Topological space

Cohomology

8. PHEW!

Why is it important?

Functions on topological space - homotopy

We have functions in programming (see my session about Type Theory :D )

And we can represent them under a topological perspective

But we need the tools from Algebraic Geometry

9. What I learned

Maths - even if it sounds useless, it might be useful at some point

We need more content connecting the pieces

Analogy: math fields are like bad-planned micro services. 

9. What I learned

Keep it simple! :)

References

Thank you :)

Questions?

 

hannelita@gmail.com

@hannelita