Motivation

Numerous computations and tasks become simple by properly sorting information in advance.

phone: 500$  
bike: 100$  
knife: 10$ 
purse: 60$ 
shoe: 70$ 
calculator: 15$ 
keyboard: 40$  
shovel: 20$ 
lawnmower: 200$ 
scissors: 5$

scissors: 5$
knife: 10$ 
calculator: 15$ 
shovel: 20$ 
keyboard: 40$  
purse: 60$ 
shoe: 70$ 
bike: 100$  
lawnmower: 200$ 
phone: 500$

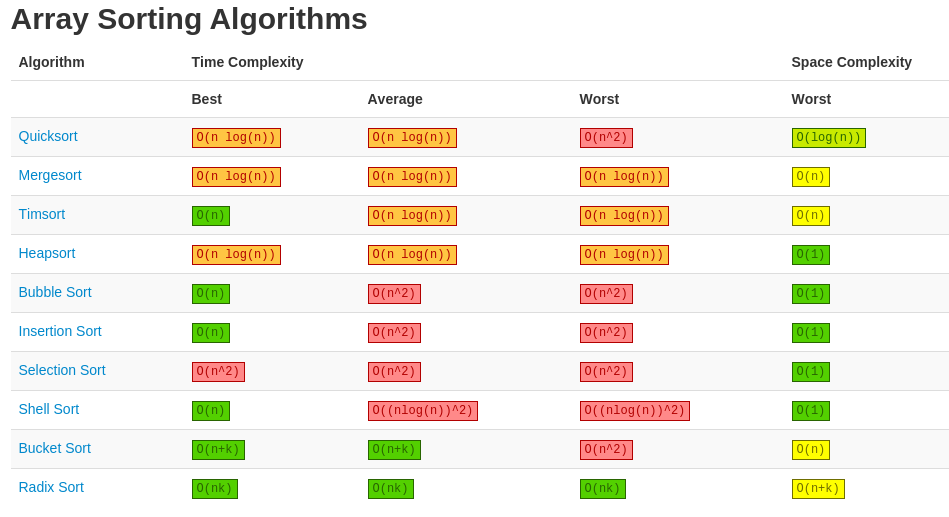
The ideal sorting algorithm would have the following properties:

  - Stable: Equal keys aren't reordered.
  - Operates in place, requiring O(1) extra space.
  - Worst-case O(n·lg(n)) key comparisons.
  - Worst-case O(n) swaps.
  - Adaptive: Speeds up to O(n) when data is nearly sorted or when there are few unique keys.

There is no algorithm that has all of these properties, and so the choice of sorting algorithm depends on the application.

Time complexity:

  - Best:    O(n^2)
  - Worst: O(n^2)

Find the smallest element using a linear scan and move it to the front. Then, find the second smallest and move it, again doing a linear scan. Continue doing this until all the elements are in place.

Selection Sort

Time complexity:

  - Best:    O(n)
  - Worst: O(n^2)

Start at the beginning of an array and swap the first two elements if the first is bigger than the second. Go to the next pair, etc, continuously making sweeps of the array until sorted.

Bubble Sort

Time complexity:

  - Best:    O(n)
  - Worst: O(n^2)

Good for a small number of elements to sort or the elements in the initial collection are already "nearly sorted". Determining when the array is "small enough" varies from one machine to another and by programming language.

Insertion Sort

Time complexity:

  - Best:    O(n + m)
  - Worst: O(n^2)

* m: number of buckets

Partition the array into a finite number of buckets, and then sort each bucket individually. This gives a time of O(n + m), where n is the number of items and m is the number of distinct items. (need to know the boundaries)

Bucket Sort

Mergesort

1) Divide and conquer

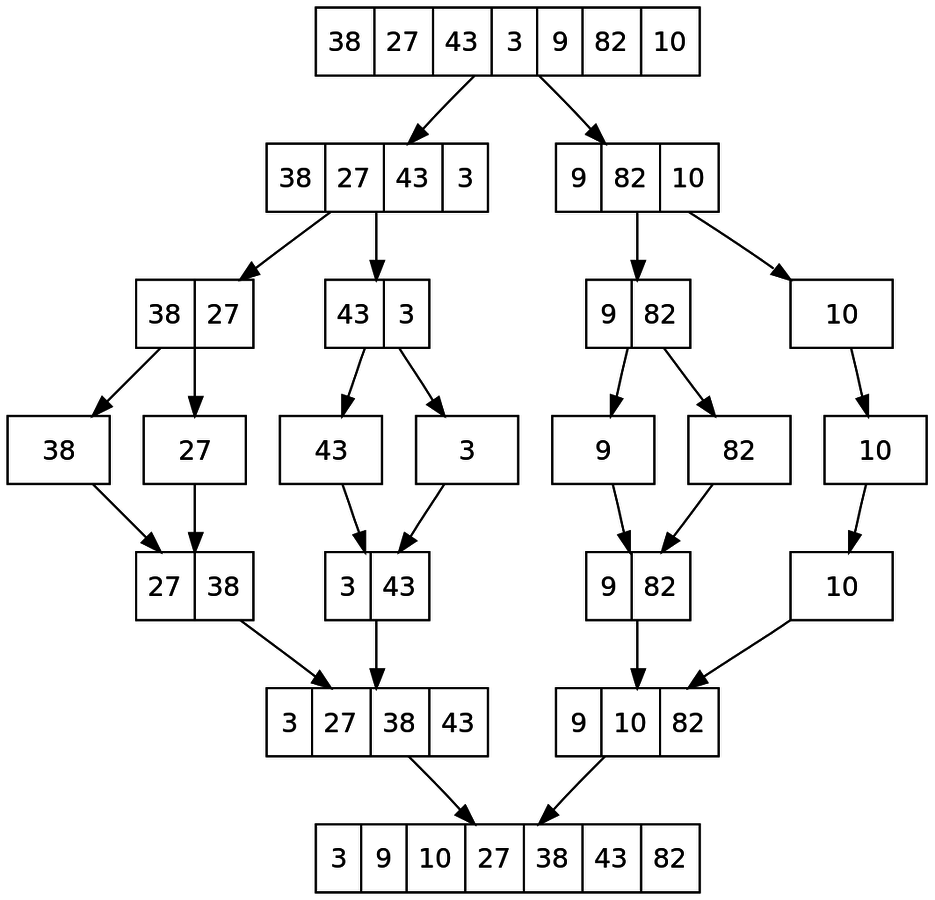
2) Recursive

1.1 Divide the array into 2 parts

 1.1 A) There are more than 1 elem

        - Continue dividing recursively 

 1.1 B) Only 1 elem

       - Return the value and merge with its siblings 

Mergesort

3) Stable

 A stable algorithm pays attention to the relationships between element locations in the original collection

Mergesort

4) May need extra temporary array

• Worst: Θ(n) extra space for arrays
• Θ(lg(n)) extra space for linked lists
  • The slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly

* Looks like is possible to do it without extra data structure but not really worthy (1) (2)

Mergesort

Time Complexity

Best:          O(n log(n))

Average:   O(n log(n))

Worst:       O(n log(n))

Is very predictable

Mergesort

When should I use it?

• when stability is required

• when sorting linked lists

• when random access is much more expensive than sequential access (for example, external sorting on tape).

Quicksort

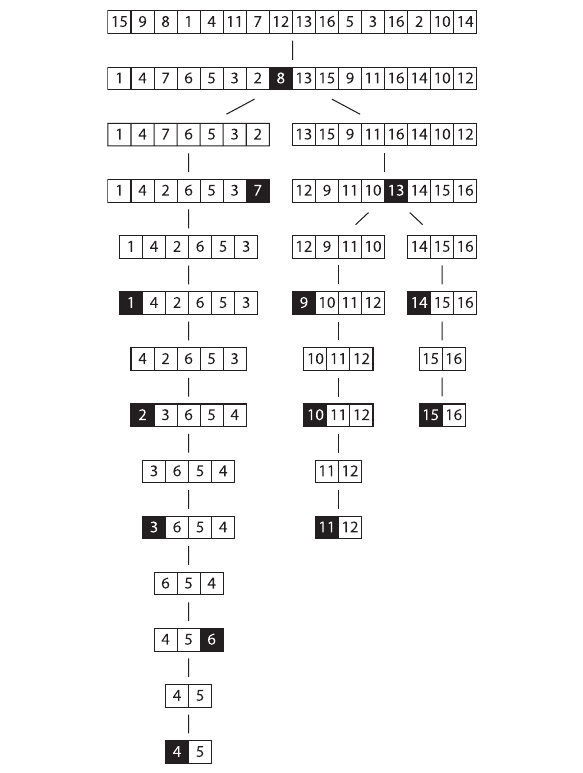
1) Divide and conquer​

2) Recursive

1.1 Pick a "pivot point". Picking a good pivot point can greatly affect the running time.
1.2 Break the list into two lists
1.3 Recursively sort each of the smaller lists.
1.4 Make one big list

qsort(left) PIVOT qsort(right)

Quicksort

4) May need extra temporary space but

• The algorithm uses O(lg(n)) extra space in the worst case.

3) Not Stable

Quicksort

Time Complexity

Best:          O(n log(n))

Average:   O(n log(n))

Worst:       O(n^2)

Quicksort

When should I use it?

• When a stable sort is NOT needed, quick sort is an excellent general-purpose sort (there is an improved version doing 3-way partitioning)

• BAD: When the data is almost sorted 

If Quicksort is O(n log n) on average, but mergesort is O(n log n) always

why not use
mergesort? Isn’t it faster?

Quicksort is faster in most cases

WHY?

: constant time to access any piece of memory on demand

C

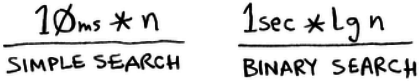
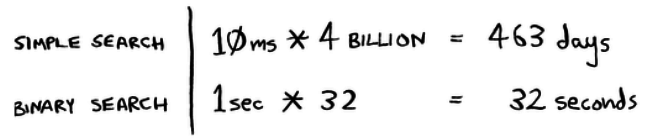
Quicksort has a smaller constant than mergesort, in this case make a difference

Quicksort is faster in most cases

WHY?

Even though complexity is quadratic in the worst case, looks like it is very rare to get this results if you choose wisely the pivot

• A good strategy is get a random pivot.

  Hits the average case way more often than the worst case.

Heap sort !?

Even though Heap sort has a good

Worst time complexity: O(n log(n))

• Is not stable
• Quicksort constant factors are smaller than the constant factors for Heapsort. To put it simply, partitioning is faster than maintaining the heap

Tim sort !?

Best time complexity: O(n)

Worst time complexity: O(n log(n))

Stable!!

it's tricky!

Merge sort + Selection sort

• Harder to implement
• Worst still O(n log(n))

Cool video and animations

http://www.ee.ryerson.ca/~courses/coe428/sorting/mergesort.html

Cool video and animations

THANKS

References

• http://www.sorting-algorithms.com/
• http://www.geeksforgeeks.org/merge-sort-for-linked-list/
• http://www.public.asu.edu/~aiadicic/sort.html

• Grokking algorithms book

• Algorithms-in-a-nutshell-in-a-nutshell book