BreakID

now also for ASP

Jo Devriendt, Bart Bogaerts,

Maurice Bruynooghe, Marc Denecker
 

University of Leuven / Aalto University

State-of-the-art static symmetry breaking for SAT ported to ASP

Outline

  • Static symmetry breaking in ASP
  • Our contribution:
    • Extending rule type support
    • More stable graph coloring encoding
    • Leveraging BreakID's improved symmetry breaking
    • Experimental results
  • Conclusion & Future work

Symmetry in ASP

  • Defined for ground pogram     with answer sets
  • Permutation    of literals   is a symmetry if
    •  
    •  
    • typically also
  • Slows down search (exponentially)
  • Often handled by posting
    lex-leader symmetry breaking
    formulas
\pi(\neg l)=\neg\pi(l)
π(¬l)=¬π(l)\pi(\neg l)=\neg\pi(l)
\mathcal{P}
P\mathcal{P}
\pi(\mathcal{P})=\mathcal{P}
π(P)=P\pi(\mathcal{P})=\mathcal{P}
\pi
π\pi
l
ll
\mathcal{A}
A\mathcal{A}
\pi(\mathcal{A})=\mathcal{A}
π(A)=A\pi(\mathcal{A})=\mathcal{A}

Static symmetry breaking in ASP

ASP program in standard form (Lparse-Smodels)

Ground ASP program

Ground ASP program + symmetry breakers

Ground ASP program as a colored graph

Grounding

"Graphing"

Automorphism detection + symmetry breaking formula construction

"Graphing"

h_1\vee \ldots \vee h_l \leftarrow a_1 \wedge \ldots \wedge a_n \wedge \neg b_1 \wedge \ldots \wedge \neg b_m
h1∨…∨hl←a1∧…∧an∧¬b1∧…∧¬bmh_1\vee \ldots \vee h_l \leftarrow a_1 \wedge \ldots \wedge a_n \wedge \neg b_1 \wedge \ldots \wedge \neg b_m

Graph encoding of standard rule    :

Graph encoding of literal   :

l
ll
r
rr

"Graphing"

h \leftarrow g \leq \mathrm{sum}\{a_1=w_1, \ldots, a_n=w_n, \neg b_1=w_{n+1}, \ldots, \neg b_m=w_{n+m}\}
h←g≤sum{a1=w1,…,an=wn,¬b1=wn+1,…,¬bm=wn+m}h \leftarrow g \leq \mathrm{sum}\{a_1=w_1, \ldots, a_n=w_n, \neg b_1=w_{n+1}, \ldots, \neg b_m=w_{n+m}\}

Graph encoding of integer     :

Graph encoding of weight rule    :

w
ww
r
rr

"Graphing"

  • BreakID also supports
    • Choice rule
    • Minimize rule
  • == Lparse-Smodels + Disjunctive rules
  • (6 + #weights) colors
  • (#heads + #bodies + #weights + #literals) nodes
  • O(    ) edges
\mathcal{P}
P\mathcal{P}

Difference with SBASS (alternative ASP symmetry breaker)

  • support for Minimize and Weight rule
  • undirected edges

"Graphing"

\mathcal{P}\colon
P:\mathcal{P}\colon
  • SBASS detects no symmetry?
  • BreakID detects interchangeability of {p,q}
0 \leq \#\{p\} \leq 1.
0≤#{p}≤1.0 \leq \#\{p\} \leq 1.
0\leq \#\{q\} \leq 1.
0≤#{q}≤1.0\leq \#\{q\} \leq 1.

Hypothesis: Saucy only supports undirected edges

Symmetry breaking formulae
of BreakID

Motivating example for BreakID: pigeonhole problem

Only 2 more instances solved?

Let's try Shatter on the pigeonhole problem...

Only 2 more instances solved?

  • Problem lies with generator symmetries Σ
  • <Σ> is not completely broken by conjunction of sbf(σ), σ∈Σ
  • For pigeonhole, there does exist some small Σ' for which sbf(σ), σ∈Σ' breaks <Σ> completely

In general, Σ lacks information on structure of group <Σ>

Symmetry breaking formula

BreakID tries to exploit symmetry group structure

  • Detect row interchangeability symmetry subgroups
  • Symmetry breaking based on stabilizer chain of symmetry group
  • Small performance optimizations

Symmetry breaking formulae

  • Row interchangeability: common form of symmetry
    • Stems from interchangeable objects
    • Variables can be ordered as rows in matrix
    • All permutations of rows are symmetries
  • Can be broken completely by constructing symmetry breaking formula only for consecutive row swaps
    • Assuming appropriate variable ordering

Symmetry breaking formulae

Detecting row interchangeability

Occupies(p1,h1) Occupies(p1,h2) Occupies(p1,h3)
Occupies(p2,h1) Occupies(p2,h2) Occupies(p2,h3)
Occupies(p3,h1) Occupies(p3,h2) Occupies(p3,h3)
Occupies(p4,h1) Occupies(p4,h2) Occupies(p4,h3)

Variable rows for 4 pigeons, 3 holes:

Symmetry due to interchangeable pigeons completely broken by

sbf(swap(p1,p2)) ∧ sbf(swap(p2,p3)) ∧ sbf(swap(p3,p4))

Detecting row interchangeability

  • Input: CNF theory T, Σ detected by Saucy
  • Output: variable matrix M such that rows are interchangeable and <M>⊆<Σ>
  1. extract σ1, σ2 ∈Σ that form 2 subsequent row swaps
    • forms initial 3-rowed variable matrix M
  2. apply every σ∈Σ to all detected rows r∈M so far
    • images σ(r) disjoint of M are candidates to extend M
    • test if swap r ↔ σ(r) is a symmetry by syntactical check on T
    • if success, extend M with σ(r)
  3. use Saucy to extend Σ with new symmetry generators by fixing all variable nodes with variable in M, first row excepted

Let's try BreakID on the pigeonhole problem,
while detecting row interchangeability

  • Detects full pigeon subsymmetry and hole subsymmetry
  • Poly performance
  • 100+ holes are no problem
     

Symmetry breaking formulae

  • If symmetry    stabilizes literal   , then
                 

    is a valid lex-leader symmetry breaking formula for symmetry group
  • BreakID maximizes the number of binary symmetry breaking clauses
    • by adjusting variable order
\neg l \vee \pi(l)
¬l∨π(l)\neg l \vee \pi(l)
\pi
π\pi
l
ll

Symmetry breaking formulae

BreakID derives binary symmetry breaking clauses
based on chains of stabilizer subgroups

Stabilizer chain symmetry breaking

\forall i\colon (\forall j < i \colon x_j \Leftrightarrow \sigma(x_j)) \Rightarrow \neg x_i \vee \sigma(x_i)
∀i:(∀j<i:xj⇔σ(xj))⇒¬xi∨σ(xi)\forall i\colon (\forall j < i \colon x_j \Leftrightarrow \sigma(x_j)) \Rightarrow \neg x_i \vee \sigma(x_i)
  • Recall sbf(σ):
    • for i=0:
    • Binary symmetry breaking clause
       
  • x is stabilized by <Σ> iff σ(x)=x for all σ∈<Σ>
  • x' ∈ orbit(x) under <Σ> iff there exists σ∈<Σ> s.t. σ(x)=x'
     
  • Given symmetry group <Σ> with smallest non-stabilized variable x, with x' ∈ orbit(x) under <Σ>,
                   is logical consequence of sbf(σ) for all σ∈<Σ>
     
  • Moreover, all binary clauses in sbf(σ) for all σ∈<Σ> are derived this way [4]
\neg x_0 \vee \sigma(x_0)
¬x0∨σ(x0)\neg x_0 \vee \sigma(x_0)
\neg x \vee x'
¬x∨x′\neg x \vee x'

Stabilizer chain symmetry breaking

  • <Σ> has subgroups that have other smallest non-stabilized variables, depending on variable order
  • Create stabilizer chain of <Σ> along variable ordering:
     
  • next subgroup Gi is the stabilizer subgroup stabilizing the next non-stabilized variable in ordering
    • Gi have different smallest non-stabilized variables x
  • for each i: Orbit(x) under Gi leads to binary symmetry breaking clauses
    • Derives all binary symmetry breaking clauses of <Σ> under variable ordering
<\Sigma> = G_0 \supset G_1 \supset \ldots \supset 1
<Σ>=G0⊃G1⊃…⊃1<\Sigma> = G_0 \supset G_1 \supset \ldots \supset 1

Stabilizer chain symmetry breaking

Occupies(p1,h1) Occupies(p1,h2) Occupies(p1,h3)
Occupies(p2,h1) Occupies(p2,h2) Occupies(p2,h3)
Occupies(p3,h1) Occupies(p3,h2) Occupies(p3,h3)
Occupies(p4,h1) Occupies(p4,h2) Occupies(p4,h3)

Occupies(p1 ,h1) < Occupies(p2 ,h1) < Occupies(p3 ,h1) < Occupies(p4 ,h1) < ...

Stabilizer chain for pigeon symmetry consists of 4 subgroups

G0 permutes rows 1-2-3-4,
G1 permutes rows 2-3-4,
G2 swaps rows 3-4,
G3=1

Binary symmetry breaking clauses:

¬Occupies(p1 ,h1) v Occupies(p2 ,h1)
...
¬Occupies(p3 ,h1) v Occupies(p4 ,h1)

  • More compact conversion of sbf to CNF [5]
    • 3 clauses of size 3 instead of
      4 clauses of sizes 3-4
  • Limit the size of symmetry breaking formula to 50
  • Limit symmetry detection time of Saucy

Symmetry breaking formulae

BreakID's small optimizations compared to Shatter / Sbass

Symmetry breaking in SAT competitions?

  • BreakID overhead is low enough to be competitive, even on asymmetric instances
  • Participated succesfully in SAT13, SAT15 competitions
  • Experimental results on SAT14 instances
    (Glucose as base solver)

Summary

  • BreakID follows in Shatter's footsteps (after ~10 years!)
  • Derive group structure information
    • Row interchangeability detection
    • Stabilizer chain based symmetry breaking
      • Both are approximative algorithms
  • Efficiency optimizations ensure competitiveness

Experimental comparison
of BreakID and SBASS

1000s timeout

Experimental comparison
of BreakID and SBASS

50 000s timeout

Conclusion

  • BreakID also works in an ASP setting
  • Supports two extra rule types
  • More robust due to undirected edges
  • More efficient due to smarter symmetry breaking formulas

Future work?

  • Symmetry detection on predicate level
    • Paper presentation next friday ;)
  • Dynamic symmetry breaking
    • Work underway, ready by SAT17 :)

Future of symmetry handling

ASP program in standard form (Lparse-Smodels)

Ground ASP program

Ground ASP program + symmetry breakers

Ground ASP program as a colored graph

Grounding

"Graphing"

Automorphism detection + symmetry breaking formula construction

Predicate level symmetry detection

Symmetry handling during search

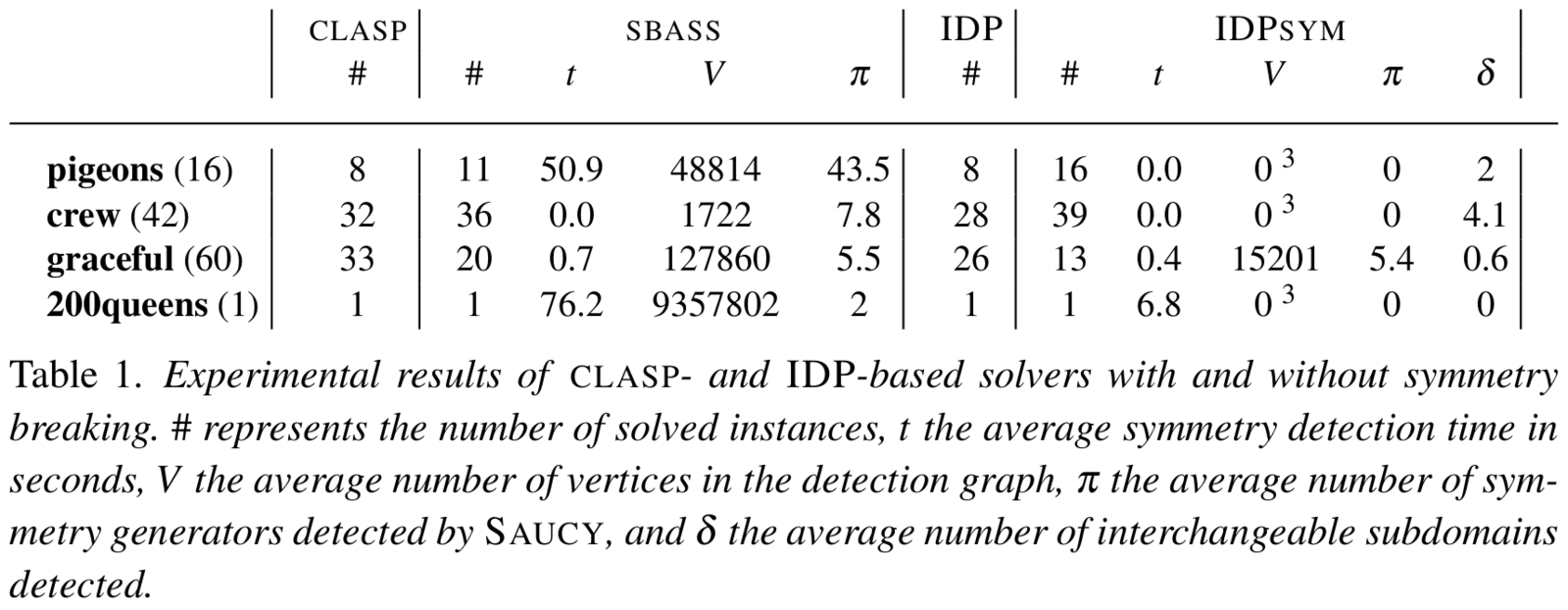
Experimental comparison
of IDP and SBASS

1000s timeout

Thanks for your attention!

Questions?

[0] Improved Static Symmetry Breaking for SAT - 2016 - Devriendt et al.
[1] Symmetry and Satisfiability: An Update - 2010 - Katebi et al.
[2] Efficient Symmetry-Breaking for Boolean Satisfiability - 2006 - Aloul et al.
[3] On the importance of row symmetry - 2014 - Devriendt et al.
[4] Automatic generation of constraints for partial symmetry breaking - 2011 - Jefferson & Petrie
[5] Symmetry and satisfiability - 2009 - Sakallah
[6] On Local Domain Symmetry for Model Expansion - 2016 - Devriendt et al. (presentation Friday)
[7] Symmetry-breaking Answer Set Solving - 2011 - Drescher et al.

Made with Slides.com