Ominaislämpökapasiteetti
c on aineen ominaislämpökapasiteetti
Ominaislämpökapasiteetti (c) kuvaa
- kuinka paljon aineeseen sitoutuu
- kuinka paljon aineesta vapautuu
lämpöenergiaa (Q) yhtä kilogrammaa ja yhden kelvinasteen lämpötilamuutosta kohti.
Q vapautuva/sitoutuva lämpöenergia
on aineen lämpötilamuutos
Ominaislämpökapasiteetti
Esimerkki
Järvivettä kannetaan saunan pesutupaan 30 l.
Kuinka paljon järviveteen pitää lisätä kiukaan vedenlämmittimestä+80 asteista vettä, jotta saadaan +37 asteista pesuvettä?
Järviveden lämpötila on +10 celsiusastetta.

lähde: Harvia.fi
Ratkaisu
Kirjataan lähtöarvot
Kuuman veden luovuttama lämpöenergia on yhtä suuri kuin kylmän veden vastaanottama lämpöenergia.
Tarkastellaan kuuman ja kylmän veden muodostamaa systeemiä eristettynä
Tapa I
Ratkaisu
Kirjataan lähtöarvot
Kuuman veden luovuttama lämpöenergia on yhtä suuri kuin kylmän veden vastaanottama lämpöenergia.
Tarkastellaan kuuman ja kylmän veden muodostamaa systeemiä eristettynä
Vastaus: noin 19 litraa
Tapa II
Esimerkki

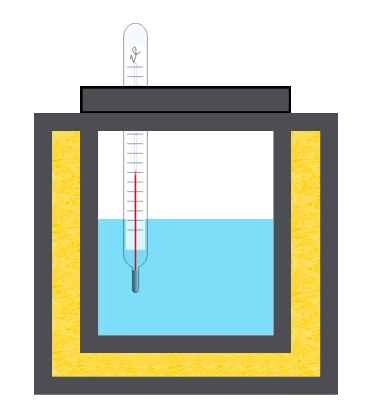
Kalorimetrissa on 600 grammaa vettä lämpötilassa +25,0 celsiuastetta.
Kalorimetrin lämpökapasiteetti on 120 J/K. Alumiinikappale, jonka massa on 220 grammaa, lämmitetään kiehuvassa vedessä.
Lämmityksen jälkeen alumiinikappale laitetaan kalorimetriin.
Kalorimetrissä olevan veden ja alumiinikappaleen loppulämpötilaksi mitataan +30,2 celsiusastetta.
Laske alumiinin ominaislämpökapasiteetti.











Ratkaisu
Kirjataan lähtöarvot
Tarkastellaan kalorimetrin, siellä olevan veden ja alumiinkappaleen muodostamaa systeemiä eristettynä.

kalorimetri, vesi lämpenevät
alumiini jäähtyy
Esimerkki
Sähkökiukaan teho on 6,0 kW. Kuinka kauan kestää lämmittää 21 kuutiometriä ilmaa +20 celsiuasteen lämpötilasta +80 celsiusasteeseen? Saunan lämpökapasiteetti on 180 kJ/K.

CC BY SA 3.0 Todtanis
Ratkaisu
Kiukaan tekemä lämmitystyö on yhtä suuri kuin saunan ja saunassa olevan ilman vastaanottama lämpöenergia.
Kirjataan lähtöarvot
Tarkastellaan kiuasta, saunaa ja saunassa olevaa ilmaa eristettynä systeeminä.
Sijoitetaan tunnetut lukuarvot
Vastaus: Saunan lämmitykseen kuluu noin 46 minuuttia.
Fysiikan ylioppilaskoe
Syksy 2011 Tehtävä 3

Ratkaisu a-kohtaan
Oletetaan, että hauki on pääosin vettä.
Hauen lämpökapasiteetti saadaan laskettua
Kirjataan lähtöarvot
ominaislämpökapasiteetin avulla.
lämpökapasiteetti
veden

Ratkaisu b-kohtaan
Oletetaan, että mikroaaltouunin tekemä lämmitystyö kuluu veden lämmittämiseen ja että lämpöhäviöitä ei ole.
Kirjataan lähtöarvot

Vesi lämpenee 27 celsiusastetta.
Vastaus:
Ratkaisu c-kohtaan
Oletetaan, että vesi ei vastaanota lämpöenergiaa ympäristöstä, mutta kykenee luovuttamaan lämpöenergiaa ympäristöön vapaasti.
1. Vesi kylmenee
2. Vesi jäätyy
3. Jää kylmenee
Vastaus:
Vedestä on poistettava lämpöenergiaa noin 82 kJ.



