t ( s ) T (  C)
300     19.7
600 20.4
900 20.9
1200  21.4
1500  21.8
1800   22.3
^\circ

Mittauksen suoritus

2,5 \text{ W}

....

Mitataan systeemin lämpötilaa ajan funktiona, kun systeemiin tuodaan energiaa uppokuumentimen avulla.

Systeemi koostuu kalorimetrista ja sen sisällä olevasta

  • uppokuumentimesta
  • lämpömittarista
  • vedestä
  • ilmasta

Oletetaan systeemi eristetyksi

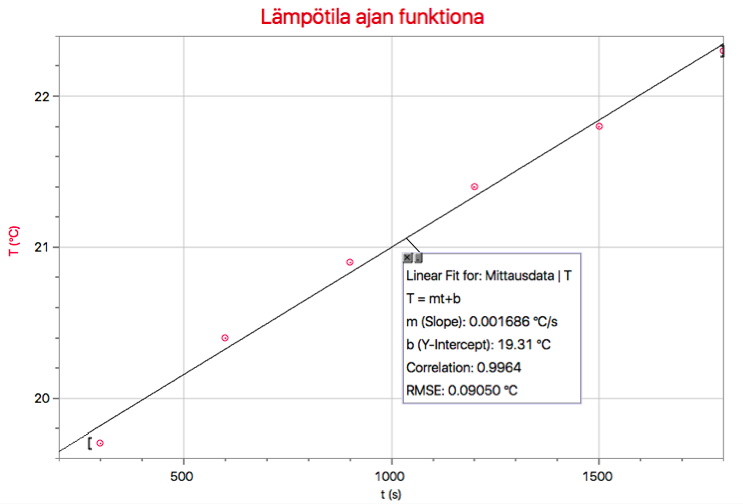
Huomataan, että systeemin lämpötila on suoraan verrannollinen kuluneeseen aikaan.

T ~ t 

t ( s )

T (  C)

Q = Pt ( J )

300    

19.7

 750 

600

20.4

1500

900

20.9

2250

1200 

21.4

3000

1500

 21.8

3750

1800  

  22.3

4500

MITTAUSTULOSTEN KÄSITTELY

^\circ

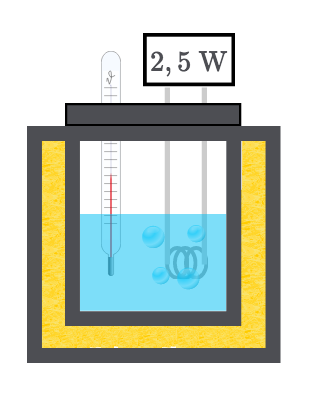
Oletetaan, että systeemi on eristetty. 

Uppokuumentimen lämmitystyö W muuttuu kokonaan systeemin lämpöenergiaksi Q.

W= Q
Pt= Q
2,5 \text{ W} \cdot 300 \text{ s} = 750 \text{ J}

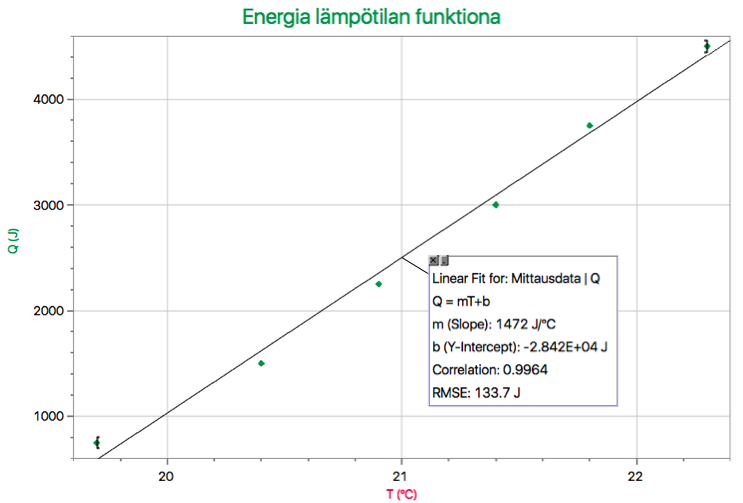
Huomataan, että systeemin lämpöenergia on suoraan verrannollinen lämpötilaan.

Q ~ T 

\dfrac{\Delta Q}{\Delta T}=\text{vakio}

Tämä vakio määritellään kappaleen lämpökapasiteetiksi C.

eli

\dfrac{\Delta Q}{\Delta T}=C

Lämpökapasiteetti

Q=C\Delta T

C on kappaleen lämpökapasiteetti

Lämpökapasiteetti (C) kuvaa 

  • kuinka paljon kappaleeseen sitoutuu
  • kuinka paljon kappaleesta vapautuu

lämpöenergiaa (Q) yhden kelvinasteen lämpötilamuutosta kohti.

Q vapautuva/sitoutuva lämpöenergia

on kappaleen lämpötilamuutos

\Delta T

Esimerkki

Teräskattilan lämpökapasiteetti on 0,91 kJ/K.

Kuinka paljon kattilan lämpötila muuttuu, kun sitä lämmitetään 250 W teholla 2,0 minuutin ajan? 

Ratkaisu

Kirjataan lähtöarvot

P=250 \text{ W}, \ t=120 \text{ s}, \ C=910 \text{ J/K}

Oletetaan, että teräskattilan vastaanottama lämpöenergia on yhtä suuri kuin tehty lämmitystyö.

Q=W
C\Delta T=Pt
||:C
\Delta T= \dfrac{Pt}{C}
\Delta T= \dfrac{250 \text{ W} \cdot 120 \text{ s}}{910 \text{ J/K}}
\Delta T \approx 32, 97\text{ K}

Vastaus: Lämpötila kasvaa

                      noin 33 celsiusastetta.

Suuri lämpökapasiteetti

PIENI lämpökapasiteetti

Kappaleeseen siirtyy 
paljon lämpöenergiaa

Kappaleen lämpötila  nousee vain vähän

Suuret lämpöenergian muutokset aiheuttavatvain pienen lämpötilan muutoksen.

Pienetkin lämpöenergian muutosket aiheuttavat suuren lämpötilan muutoksen.

Kappale luovuttaa paljon lämpöenergiaa

Kappaleen lämpötila pienenee vain vähän

Kappaleeseen siirtyy 
paljon lämpöenergiaa

Kappaleen lämpötila  nousee paljon

Kappale luovuttaa paljon lämpöenergiaa

Kappaleen lämpötila pienenee paljon