Fysiikan ylioppilaskoe S2008
Ratkaisu
Kirjataan lähtöarvot
m_k=5,2 \text{ kg}, \ m_t = 1,2 \text{ kg}
mk=5,2 kg, mt=1,2 kg
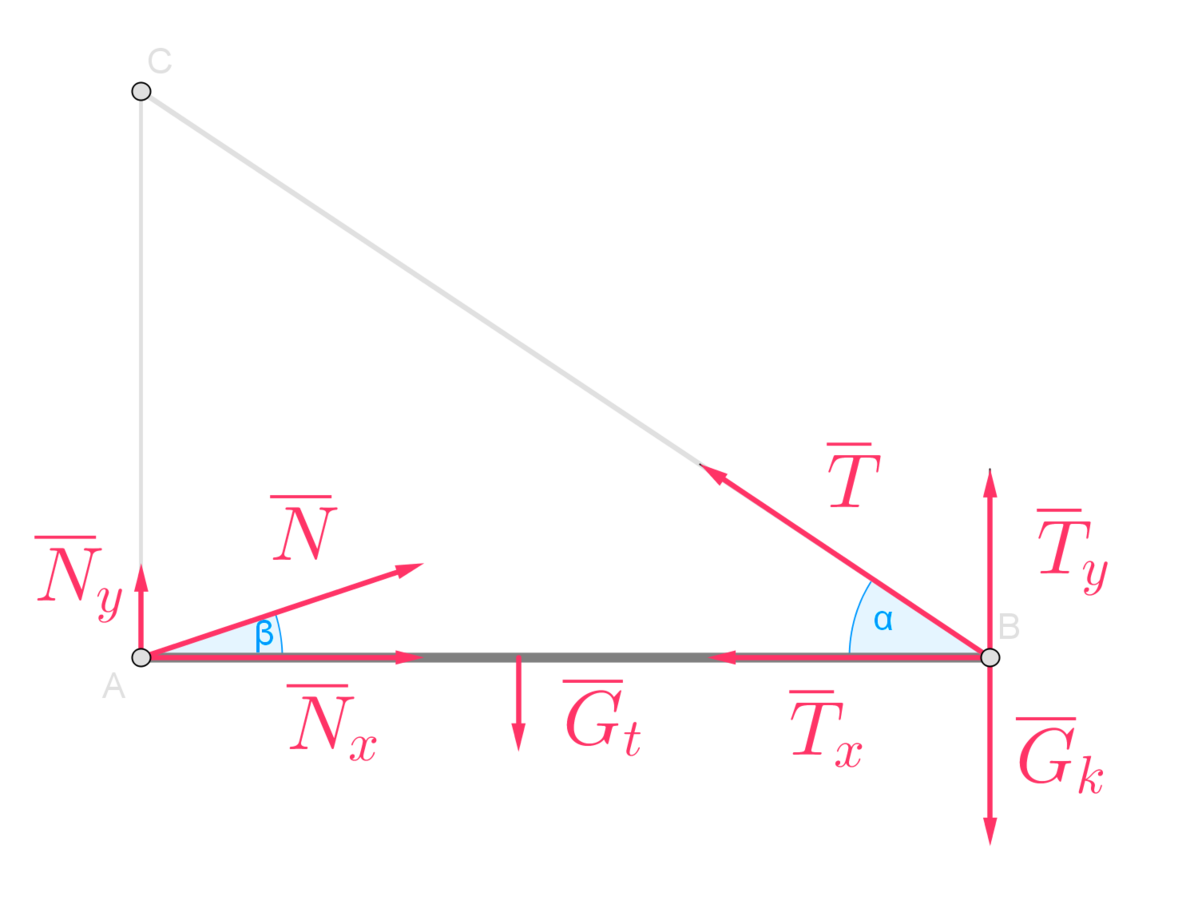
Piirretään tangon voimakuvio.
Tanko on tasapainossa etenemisen ja pyörimisen suhteen.
\text{NII } \sum \overline{F}=\overline{0}
NII ∑F=0
\sum M_A=0
∑MA=0
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
h=0,42 \text{ m}, l=0,65 \text{ m}
h=0,42 m,l=0,65 m
Ratkaistaan kulma
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
\tan \color{CornflowerBlue}\alpha=\dfrac{0,42 \text{ m}}{0,65 \text{ m}}
tanα=0,65 m0,42 m
\color{CornflowerBlue}\alpha
α
\color{CornflowerBlue}\alpha \approx 32,869^\circ
α≈32,869∘
\sum M_A=0
∑MA=0
0,42 \text{ m}
0,42 m
-G_t \dfrac{l}{2} - G_k l +T_y l=0
−Gt2l−Gkl+Tyl=0
T_y l=G_t \dfrac{l}{2} + G_k l
Tyl=Gt2l+Gkl
T_y =\dfrac{1}{2}G_t + G_k
Ty=21Gt+Gk
T \sin \color{CornflowerBlue} \alpha =\dfrac{1}{2}G_t + G_k
Tsinα=21Gt+Gk
0,65 \text{ m}
0,65 m
T=\dfrac{\frac{1}{2}G_t + G_k}{\sin \color{CornflowerBlue}\alpha}
T=sinα21Gt+Gk
:\sin \alpha
:sinα
:l
:l
T_y=T \sin \alpha
Ty=Tsinα
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
T=\dfrac{\frac{1}{2}G_t + G_k}{\sin \color{CornflowerBlue}\alpha}
T=sinα21Gt+Gk
Lasketaan vaijerin jännitysvoiman suuruus.
T=\dfrac{\frac{1}{2}\cdot 1,2 \text{ kg} \cdot 9,81 \text{ m/s}^2 + 5,2 \text{6 kg} \cdot 9,81 \text{ m/s}^2}{\sin 32,869^\circ}
T=sin32,869∘21⋅1,2 kg⋅9,81 m/s2+5,26 kg⋅9,81 m/s2
T \approx 100 \text{ N}
T≈100 N
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
Tehdään voimatarkastelu x- ja y-suunnissa erikseen.
\sum \overline{F}_x=\overline{0}
∑Fx=0
\overline{N}_x+\overline{T}_x=\overline{0}
Nx+Tx=0
N_x - T_x =0
Nx−Tx=0
N_x =T_x
Nx=Tx
N_x =T \cos \color{CornflowerBlue}\alpha
Nx=Tcosα
Sovitaan suunnat ylös ja oikealle positiivisiksi.
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
\sum \overline{F}_y=\overline{0}
∑Fy=0
\overline{N}_y+\overline{T}_y+\overline{G}_t+\overline{G}_k=\overline{0}
Ny+Ty+Gt+Gk=0
N_y +T_y -G_t-G_k =0
Ny+Ty−Gt−Gk=0
N_y=G_t +G_k - T_y
Ny=Gt+Gk−Ty
N_y=G_t +G_k - T \sin \color{CornflowerBlue}\alpha
Ny=Gt+Gk−Tsinα
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
N_y=1,2 \text{ kg} \cdot 9,81 \text{ m/s}^2+5,2 \text{ kg} \cdot 9,81 \text{m/s}^2 - 104,84 \text{ N} \cdot \sin 32,869^\circ
Ny=1,2 kg⋅9,81 m/s2+5,2 kg⋅9,81m/s2−104,84 N⋅sin32,869∘
Lasketaan seinän tukivoiman x- ja y-suuntaisten komponenttien suuruudet.
N_y=G_t +G_k - T \sin \color{CornflowerBlue}\alpha
Ny=Gt+Gk−Tsinα
N_y \approx 5,89\text{ N}
Ny≈5,89 N
N_x =T \cos \color{CornflowerBlue}\alpha
Nx=Tcosα
N_x =104,84 \text{ N} \cdot \sin 32,869^{\circ}
Nx=104,84 N⋅sin32,869∘
N_x \approx 88,1 \text{ N}
Nx≈88,1 N
0,42 \text{ m}
0,42 m
0,65 \text{ m}
0,65 m
Lasketaan Pythagoraan lauseen avulla seinän tukivoiman suuruus.
N=\sqrt{N_x^2+N_y^2}
N=Nx2+Ny2
N=\sqrt{(88,1 \text{ N})^2+(5,89 \text{ N})^2}
N=(88,1 N)2+(5,89 N)2
N \approx 88 \text{ N}
N≈88 N
Lasketaan tangentin avulla seinän tukivoiman suunta.
\tan \color{CornflowerBlue}\beta = \dfrac{N_y}{N_x}
tanβ=NxNy
\tan \color{CornflowerBlue}\beta = \dfrac{5,89 \text{ N}}{88,1 \text{ N}}
tanβ=88,1 N5,89 N
\color{CornflowerBlue}\beta \approx 3,8^\circ
β≈3,8∘
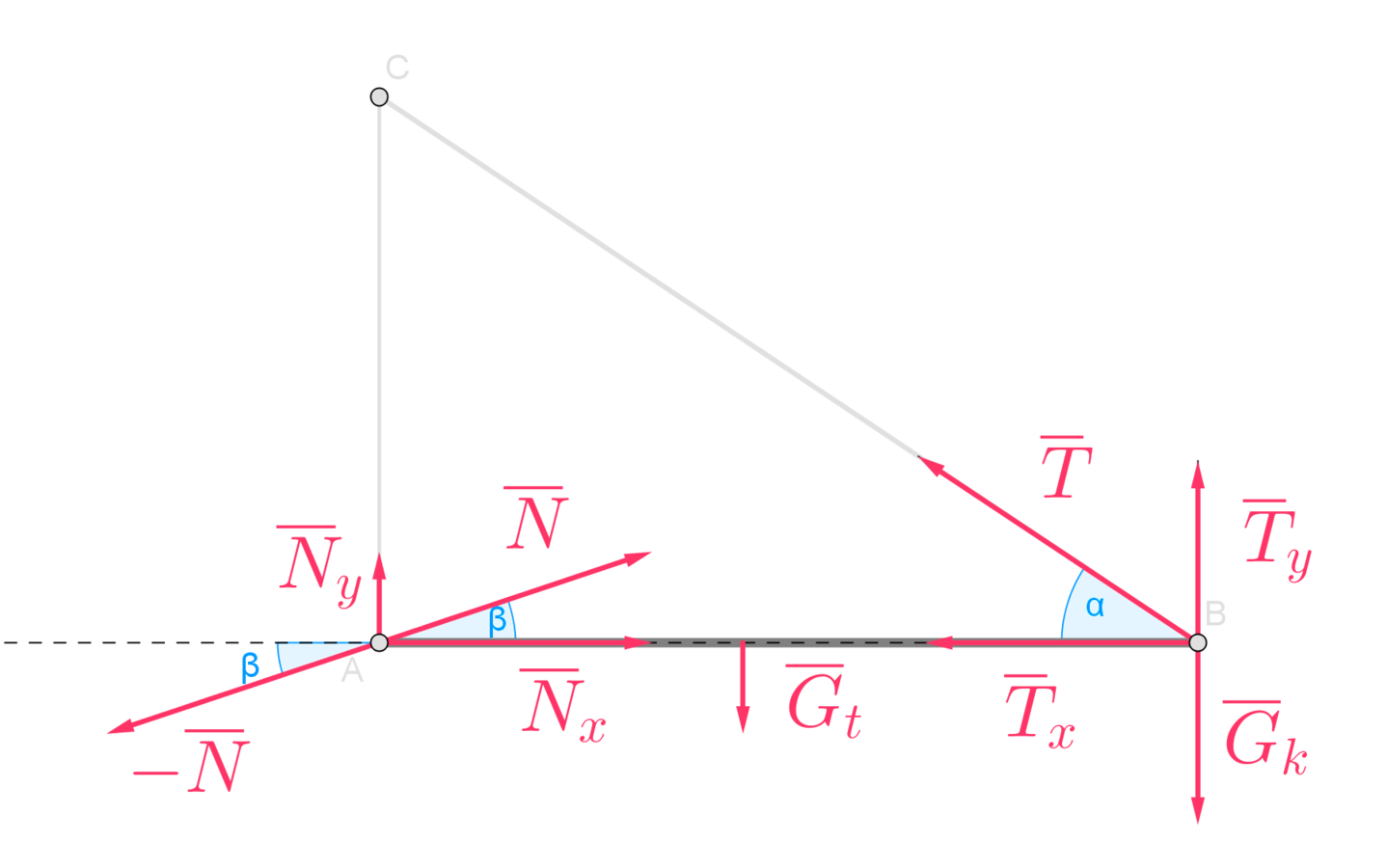
Newtonin 3. lain mukaan seinän tankoon kohdistama tukivoima on yhtä suuri kuin tangon seinään kohdistama voima, mutta vastakkaisuuntainen.
Vastaus:
Vaijerin jännitysvoiman suuruus on noin 100 N. Seinään kohdistuvan voiman suuruus on noin 88 N ja suunta poikkeaa seinän normaalista noin 3,8 astetta.
Fysiikan ylioppilaskoe S2006
Ratkaisu
Kirjataan lähtöarvot
m_1=1 \text{ kg}, \ x_1=0,32 \text{ m}
m1=1 kg, x1=0,32 m
m_2=2 \text{ kg}, \ x_2=?
m2=2 kg, x2=?
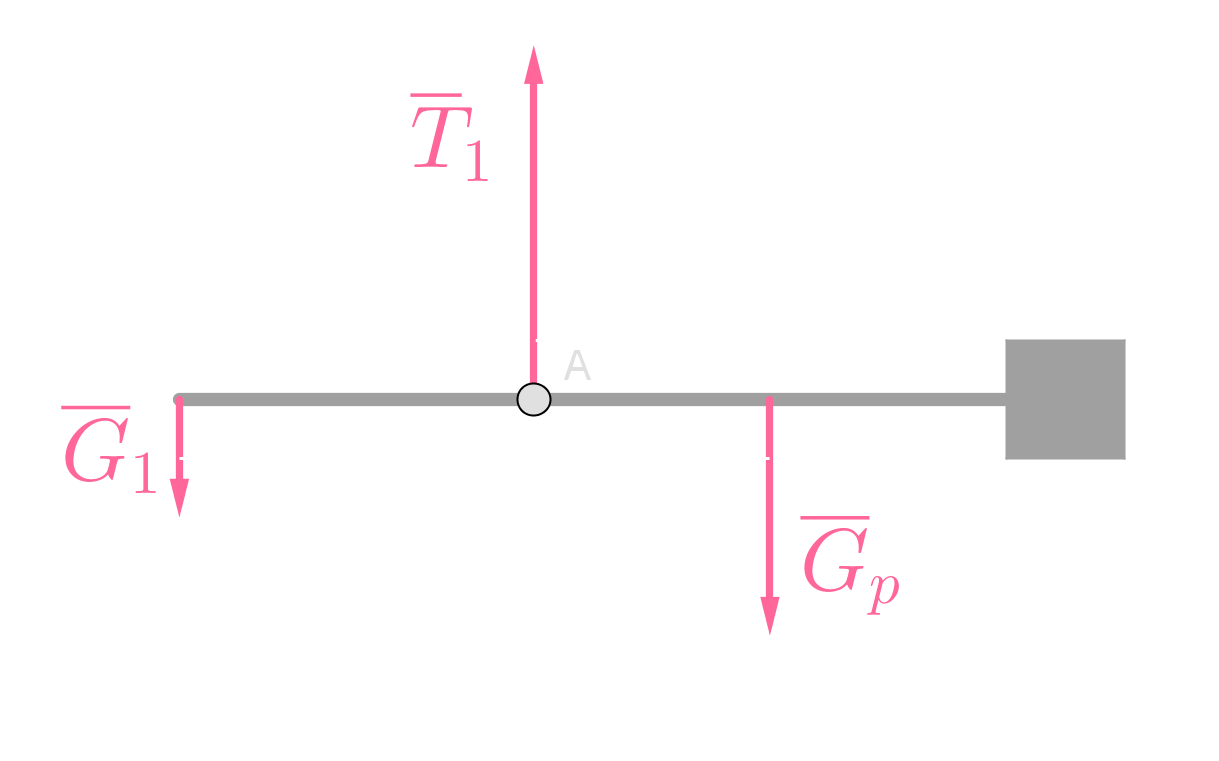
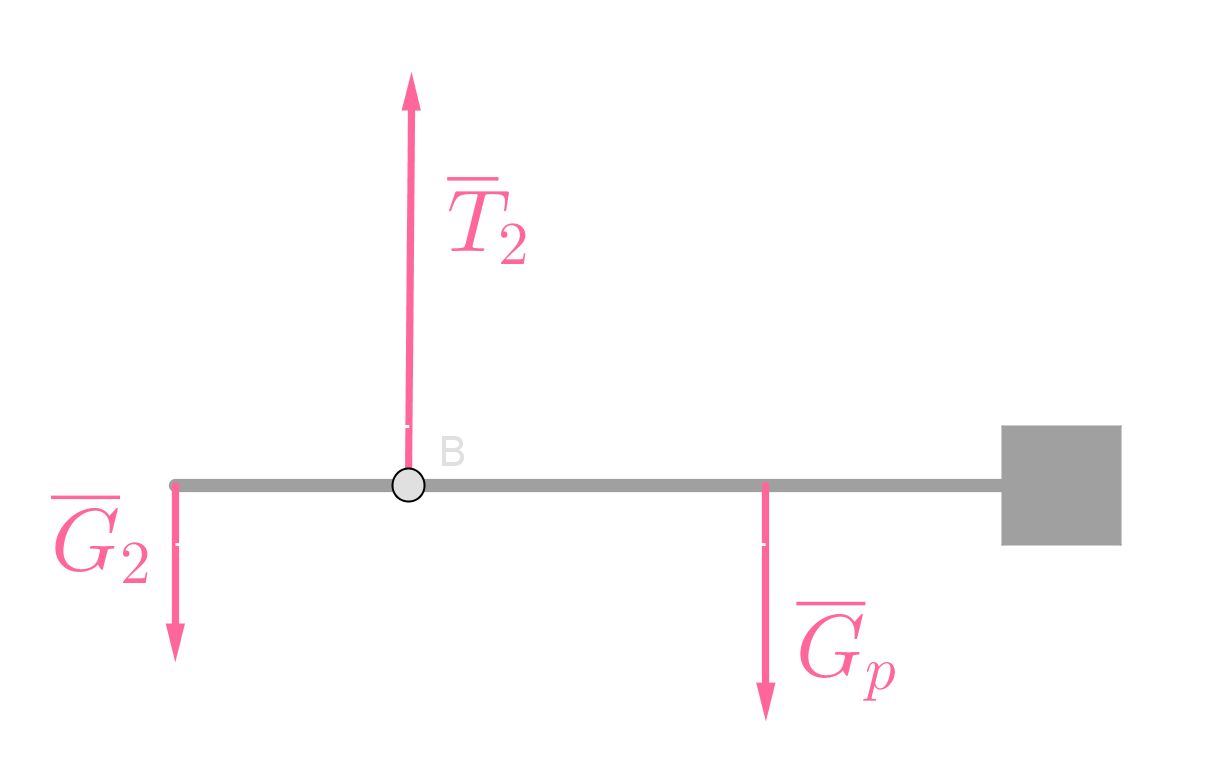
Piirretään voimakuviot tilanteista.
x_1-x_2 = 0,09 \text{ m}
x1−x2=0,09 m
1 kg:n ja 2 kg:n merkkien välimatka on 9,0 cm.
x_2 = x_1-0,09 \text{ m}
x2=x1−0,09 m
x_2 =0,32 \text{ m}-0,09 \text{ m}
x2=0,32 m−0,09 m
x_2 =0,23 \text{ m}
x2=0,23 m
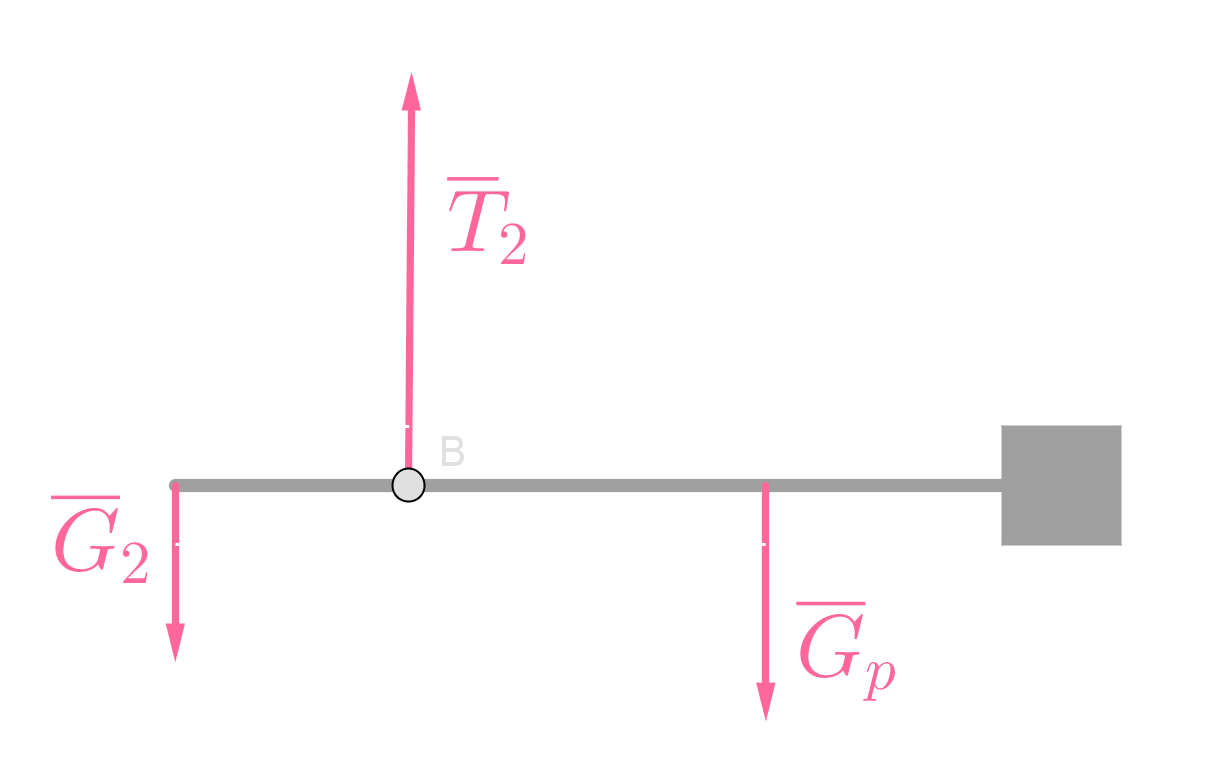
Kalavaaka on tasapainossa pyörimisen suhteen molemmissa tilanteissa.
\sum M_A = 0
∑MA=0
\color{Salmon}{G_1} x_1 - \color{Salmon}{G_p}(r-x_1)=0
G1x1−Gp(r−x1)=0
\sum M_B = 0
∑MB=0
\color{Salmon}{G_2} x_2 - \color{Salmon}{G_p}(r-x_2)=0
G2x2−Gp(r−x2)=0
\color{Salmon}{G_1} x_1 =\color{Salmon}{G_p}(r-x_1)
G1x1=Gp(r−x1)
\color{Salmon}{G_p}=\dfrac{ x_1 }{r-x_1}\color{Salmon}{G_1}
Gp=r−x1x1G1
\color{Salmon}{G_2} x_2 =\color{Salmon}{G_p}(r-x_2)
G2x2=Gp(r−x2)
\color{Salmon}{G_p}=\dfrac{ x_2 }{r-x_2}\color{Salmon}{G_2}
Gp=r−x2x2G2
Kalavaa'an paino saatiin esitettyä kahdella tavalla, joten muodostetaan näistä yhtälö.
\color{Salmon}{G_p}=\dfrac{ x_1 }{r-x_1}\color{Salmon}{G_1}
Gp=r−x1x1G1
\color{Salmon}{G_p}=\dfrac{ x_2 }{r-x_2}\color{Salmon}{G_2}
Gp=r−x2x2G2
\dfrac{ x_1 }{r-x_1}\color{Salmon}{G_1}=\dfrac{ x_2 }{r-x_2}\color{Salmon}{G_2}
r−x1x1G1=r−x2x2G2
\dfrac{ x_1 }{r-x_1}m_1g=\dfrac{ x_2 }{r-x_2}m_2g
r−x1x1m1g=r−x2x2m2g
\dfrac{ x_1 }{r-x_1}m_1=\dfrac{ x_2 }{r-x_2}m_2
r−x1x1m1=r−x2x2m2
m_1x_1(r-x_2)=m_2x_2(r-x_1)
m1x1(r−x2)=m2x2(r−x1)
G=mg
G=mg
:g
:g
\cdot(r-x_1)(r-x_2)
⋅(r−x1)(r−x2)
m_1x_1(r-x_2)=m_2x_2(r-x_1)
m1x1(r−x2)=m2x2(r−x1)
m_1x_1r-m_1x_1x_2=m_2x_2r-m_2x_1x_2
m1x1r−m1x1x2=m2x2r−m2x1x2
m_1x_1r-m_2x_2r=m_1x_1x_2-m_2x_1x_2
m1x1r−m2x2r=m1x1x2−m2x1x2
r(m_1x_1-m_2x_2)=m_1x_1x_2-m_2x_1x_2
r(m1x1−m2x2)=m1x1x2−m2x1x2
r=\dfrac{m_1x_1x_2-m_2x_1x_2}{m_1x_1-m_2x_2}
r=m1x1−m2x2m1x1x2−m2x1x2
:(m_1x_1-m_2x_2)
:(m1x1−m2x2)
Sijoitetaan lukuarvot
r=\dfrac{0,32 \text{ m} \cdot 0,23 \text{ m}(1 \text{ kg} -2 \text{ kg})}{1 \text{ kg} \cdot 0,32 \text{ m}-2 \text{ kg} \cdot 0,23 \text{ m}}
r=1 kg⋅0,32 m−2 kg⋅0,23 m0,32 m⋅0,23 m(1 kg−2 kg)
r=\dfrac{x_1x_2(m_1-m_2)}{m_1x_1-m_2x_2}
r=m1x1−m2x2x1x2(m1−m2)
\approx 0,53 \text{ m}
≈0,53 m
Fysiikan ylioppilaskoe S2008