Fysiikan ylioppilaskoe S2014

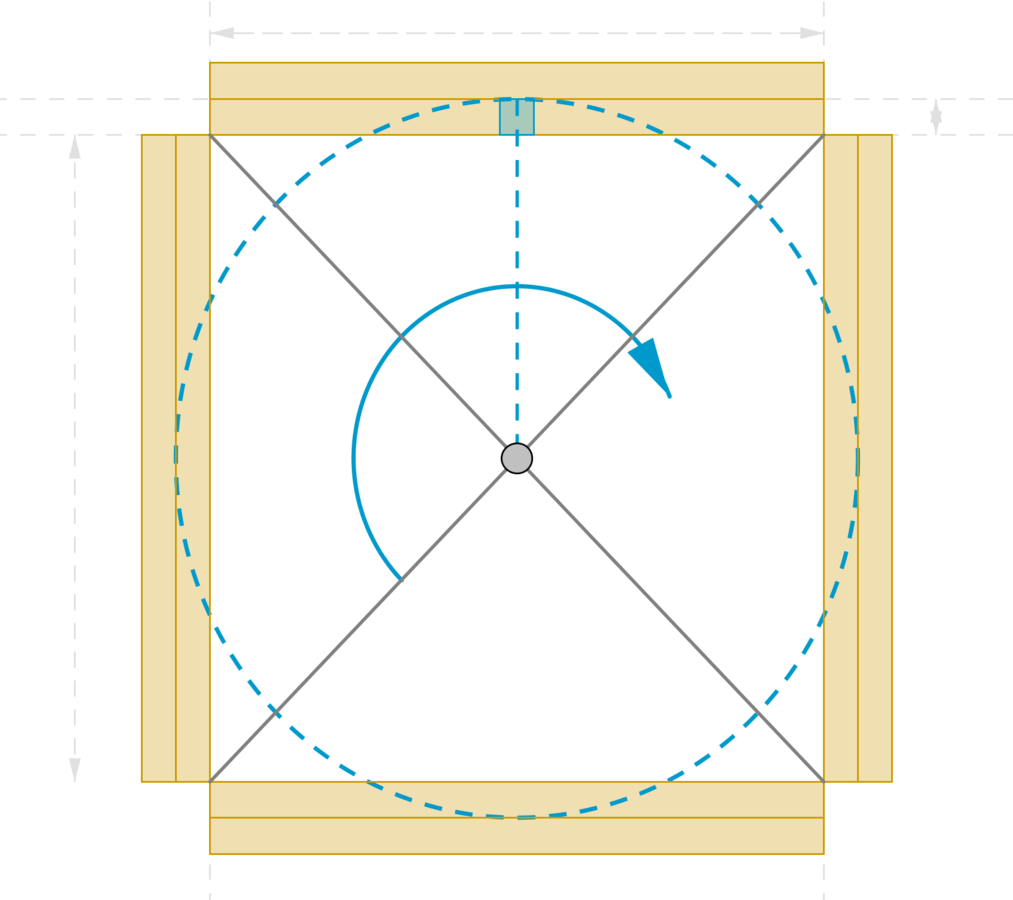
Ratkaisu

Kirjataan lähtöarvot

\omega

ω

r\color{White}{=0,14 \text{ m}}

r = 0, 14 m

r

d

d=0,015 \text{ m}

d = 0, 015 m

s

s=0,25 \text{ m}

s = 0, 25 m

\rho=1360 \frac{\text{kg}}{\text{m}^3}

ρ = 1360 \frac{​ k g ​ ​}{​ m ​ 3 ​ ​ ​}

p_r=3500 \text{ Pa}

p ​ r ​ ​ = 3500 P a

Tarkastellaan sinisellä merkittyä hunajakerroksen osaa.

m=\rho V

m = ρ V

m=\rho Ad

m = ρ A d

\omega

ω

\overline{v}

​ v ​ ​ ​

r

Oletetaan, että linko on tasaisessa pyörimisliikkeessä, jolloin tarkasteltava hunajakennon osanen on tasaisessa ympyräliikkeessä.

\overline{N}

​ N ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

Newtonin 2. lain mukaan

\sum \overline{F}=m\overline{a}

\sum ​ F ​ ​ ​ = m ​ a ​ ​ ​

\color{Salmon}{\overline{N}}=m\color{Goldenrod}{\overline{a}_n}

​ N ​ ​ ​ = m ​ a ​ ​ ​ ​ n ​ ​

\color{Salmon}{N}=m\dfrac{\color{CornflowerBlue}v^2}{r}

N = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

Hunajakennon osaseen kohdistuva paine

p=\dfrac{\color{Salmon}N}{A}

p = \frac{​ N ​ ​}{​ A ​}

, josta

\color{Salmon}N=pA

N = p A

\omega

ω

\overline{v}

​ v ​ ​ ​

r

\overline{N}

​ N ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

\color{Salmon}{N}=m\dfrac{\color{CornflowerBlue}v^2}{r}

N = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

N=pA

N = p A

m=\rho Ad

m = ρ A d

pA=\rho A d\dfrac{\color{CornflowerBlue}v^2}{r}

p A = ρ A d \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

pr=\rho d\color{CornflowerBlue}v^2

p r = ρ d v ​ 2 ​ ​

\color{CornflowerBlue}v^2=\dfrac{pr}{\rho d}

v ​ 2 ​ ​ = \frac{​ p r ​ ​}{​ ρ d ​}

\color{CornflowerBlue}v=\sqrt{\dfrac{pr}{\rho d}}

v = \sqrt ​ \frac{​ p r ​ ​}{​ ρ d ​} ​ ​ ​

\cdot \dfrac{r}{A}

\cdot \frac{​ r ​ ​}{​ A ​}

: pd

: p d

\sqrt{}

\sqrt

Selvitetään hunajakennon osasen ratanopeus.

\omega

ω

\overline{v}

​ v ​ ​ ​

r

\overline{N}

​ N ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

\color{CornflowerBlue}v=\sqrt{\dfrac{pr}{\rho d}}

v = \sqrt ​ \frac{​ p r ​ ​}{​ ρ d ​} ​ ​ ​

Hunajakenno kestää 3500 Pa suuruisen paineen, joten rajatilanteessa ratanopeudeksi saadaan

\color{CornflowerBlue}v=\sqrt{\dfrac{3500 \text{ Pa}\cdot 0,14 \text{ m}}{1360 \text{ kg/m}^3 \cdot 0,015 \text{ m}}}

v = \sqrt ​ \frac{​ 3 5 0 0 P a \cdot 0 , 1 4 m ​ ​}{​ 1 3 6 0 k g / m ​ 3 ​ ​ \cdot 0 , 0 1 5 m ​} ​ ​ ​

\color{CornflowerBlue}v=\sqrt{\dfrac{3500 \text{ Pa}\cdot 0,14 \text{ m}}{1360 \text{ kg/m}^3 \cdot 0,015 \text{ m}}}

v = \sqrt ​ \frac{​ 3 5 0 0 P a \cdot 0 , 1 4 m ​ ​}{​ 1 3 6 0 k g / m ​ 3 ​ ​ \cdot 0 , 0 1 5 m ​} ​ ​ ​

\color{CornflowerBlue}v \approx 4,901 \text{ m/s}

v \approx 4, 901 m / s

\omega

ω

\overline{v}

​ v ​ ​ ​

r

\overline{N}

​ N ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

\color{CornflowerBlue}v=\omega r

v = ω r

Muutetaan ratanopeus kierrosnopeudeksi

\omega = 2 \pi n

ω = 2 π n

\color{CornflowerBlue}v=2 \pi n r

v = 2 π n r

:2 \pi r

: 2 π r

n=\dfrac{\color{CornflowerBlue}v}{2\pi r}

n = \frac{​ v ​ ​}{​ 2 π r ​}

n=\dfrac{4,901 \text{ m/s}}{2\pi \cdot 0,14 \text{ m}}

n = \frac{​ 4 , 9 0 1 m / s ​ ​}{​ 2 π \cdot 0 , 1 4 m ​}

n \approx 5,57 \frac{1}{\text{s}}

n \approx 5, 57 \frac{​ 1 ​ ​}{​ s ​}

n \approx 330 \frac{1}{\text{min}}

n \approx 330 \frac{​ 1 ​ ​}{​ m i n ​}

Vastaus:

Linkoa voidaan pyörittää enintään 330 kierrosta minuutissa siten, että kenno ei rikkoudu.

Esimerkki

Määritä Auringon massa käyttäen hyväksesi seuraavia oletuksia ja tietoja:

Maa kiertää Aurinkoa ympyrärataa

Maan ja Auringon välinen keskietäisyys on

1,4960 \cdot 10^8 \text{ km}

1, 4960 \cdot 1 0 ​ 8 ​ ​ k m

Maan kiertoaika Auringon ympäri 365,25 d

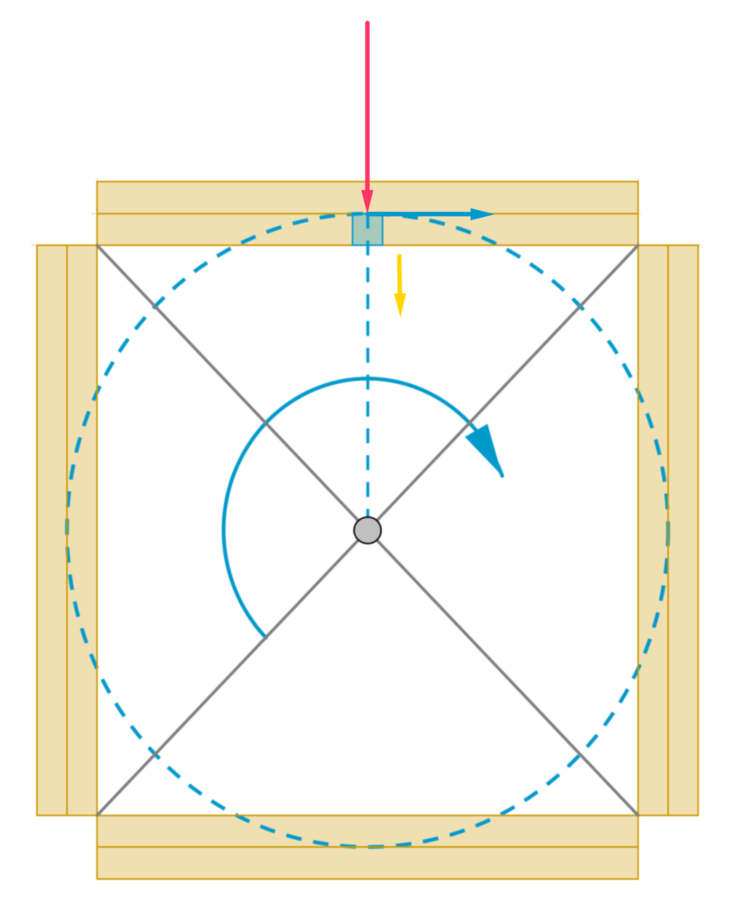
Ratkaisu

Kirjataan lähtöarvot

r=1,4960\cdot10^8 \text{ km} = 1,4960 \cdot 10^{11} \text{ m}

r = 1, 4960 \cdot 1 0 ​ 8 ​ ​ k m = 1, 4960 \cdot 1 0 ​ 11 ​ ​ m

T=365,25 \text{ d}

T = 365, 25 d

Oletetaan, että Maapallo kiertää ympyrärataa tasaisesti.

\text{NII} \ \sum \overline{F}=m\overline{a}

N I I \sum ​ F ​ ​ ​ = m ​ a ​ ​ ​

\color{Salmon}{F_1}=m\color{Goldenrod}{a_n}

F ​ 1 ​ ​ = m a ​ n ​ ​

a_n=\frac{v_m^2}{r}

a ​ n ​ ​ = \frac{​ v ​ m ​ 2 ​ ​ ​ ​}{​ r ​}

F_1=\gamma \frac{Mm}{r^2}

F ​ 1 ​ ​ = γ \frac{​ M m ​ ​}{​ r ​ 2 ​ ​ ​}

\gamma \dfrac{Mm}{r^2}=m\dfrac{\color{CornflowerBlue}{v}^2}{r}

γ \frac{​ M m ​ ​}{​ r ​ 2 ​ ​ ​} = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

: m

\gamma \dfrac{M}{r^2}=\dfrac{\color{CornflowerBlue}{v}^2}{r}

γ \frac{​ M ​ ​}{​ r ​ 2 ​ ​ ​} = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

M

m

M=\dfrac{r\color{CornflowerBlue}{v}^2}{\gamma}

M = \frac{​ r v ​ 2 ​ ​ ​ ​}{​ γ ​}

\cdot r^2

\cdot r ​ 2 ​ ​

\gamma \dfrac{M}{r^2}=\dfrac{\color{CornflowerBlue}{v}^2}{r}

γ \frac{​ M ​ ​}{​ r ​ 2 ​ ​ ​} = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\gamma M=r\color{CornflowerBlue}{v}^2

γ M = r v ​ 2 ​ ​

: \gamma

: γ

Toisaalta ratanopeus saadaan kirjoitettua muotoon

\color{CornflowerBlue}v=\dfrac{2 \pi r}{T}

v = \frac{​ 2 π r ​ ​}{​ T ​}

Fysiikan ylioppilaskoe S2006

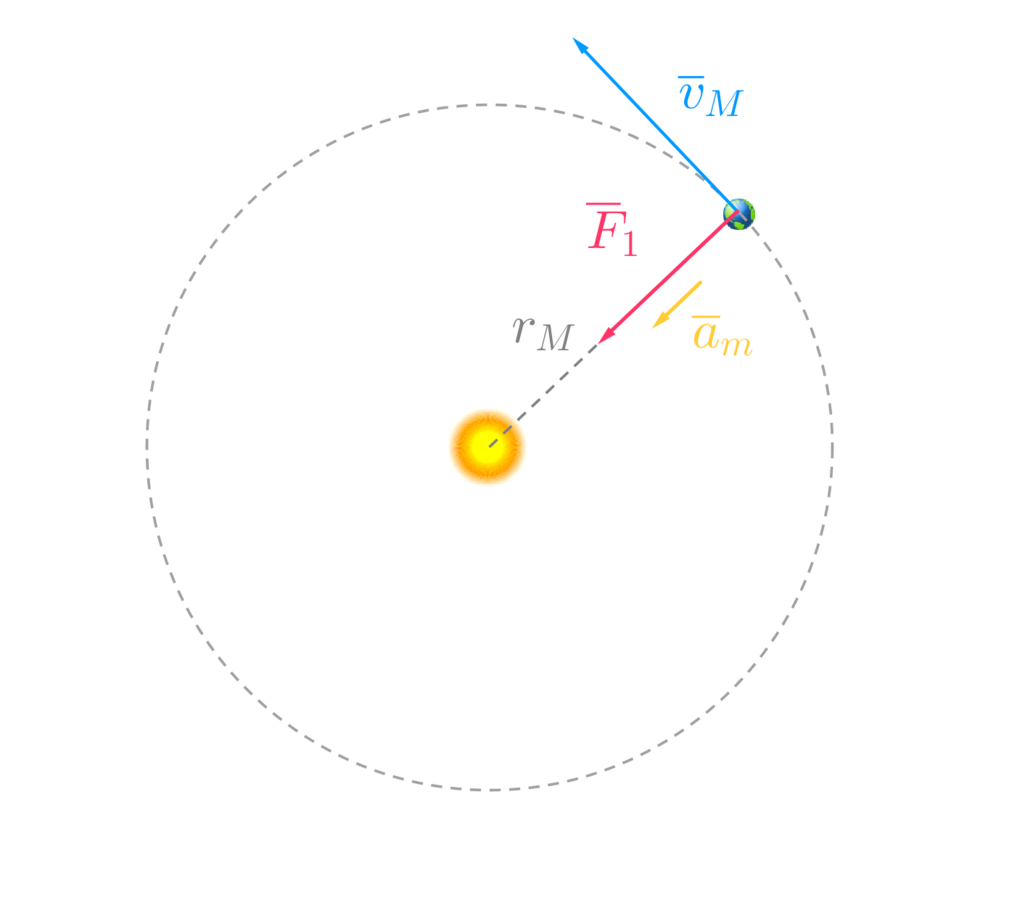
Ratkaisu

Kirjataan lähtöarvot

r_M=21 \ 000 R ,

r ​ M ​ ​ = 21000 R,

r_K = 60 R ,

r ​ K ​ ​ = 60 R,

T_K = 27,3 \text{ d}

T ​ K ​ ​ = 27, 3 d

T_M = 365 \text{ d}

T ​ M ​ ​ = 365 d

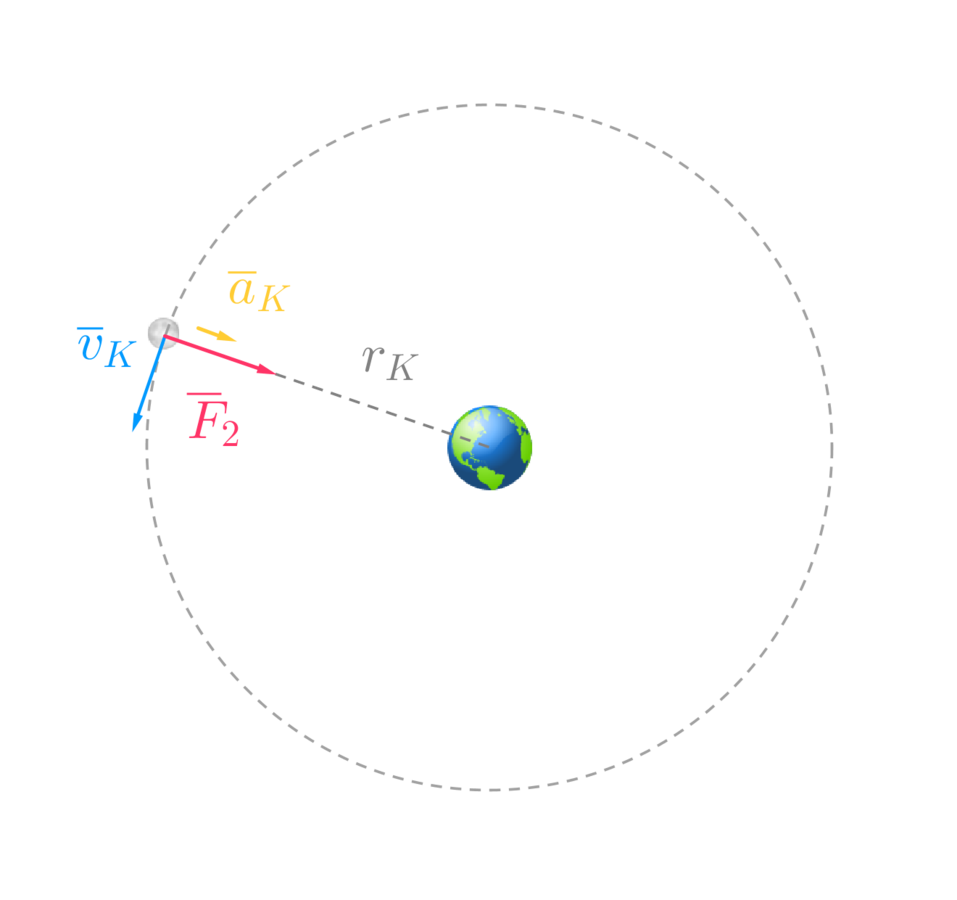
Oletetaan, että Kuu ja Maapallo ovat tasaisessa ympyräliikkeessä.

Newtonin 2. lain mukaan

\sum \overline{F}=m_1\overline{a}

\sum ​ F ​ ​ ​ = m ​ 1 ​ ​ ​ a ​ ​ ​

Newtonin gravitaatiolain nojalla saadaan

\gamma \dfrac{m_1m_2}{r^2}=m_1\dfrac{v^2}{r}

γ \frac{​ m ​ 1 ​ ​ m ​ 2 ​ ​ ​ ​}{​ r ​ 2 ​ ​ ​} = m ​ 1 ​ ​ \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\gamma \dfrac{m_2}{r^2}=\dfrac{v^2}{r}

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​ 2 ​ ​ ​} = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\gamma \dfrac{m_2}{r}=v^2

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​} = v ​ 2 ​ ​

F=m_1a

F = m ​ 1 ​ ​ a

:m_1

: m ​ 1 ​ ​

a=\frac{v^2}{r}

a = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\cdot r

\cdot r

Kappaleet kiertävät ympyrärataa, joten toisaalta ratanopeus saadaan kirjoitettua muotoon

v=\dfrac{2 \pi r}{T}

v = \frac{​ 2 π r ​ ​}{​ T ​}

\gamma \dfrac{m_2}{r}=v^2

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​} = v ​ 2 ​ ​

\gamma \dfrac{m_2}{r}=\dfrac{4 \pi^2 r^2}{T^2}

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​} = \frac{​ 4 π ​ 2 ​ ​ r ​ 2 ​ ​ ​ ​}{​ T ​ 2 ​ ​ ​}

\cdot \dfrac{r}{\gamma}

\cdot \frac{​ r ​ ​}{​ γ ​}

m_2=\dfrac{4 \pi^2 r^3}{\gamma T^2}

m ​ 2 ​ ​ = \frac{​ 4 π ​ 2 ​ ​ r ​ 3 ​ ​ ​ ​}{​ γ T ​ 2 ​ ​ ​}

Kappale, jota kierretään

Nyt saadaan kirjoitettua Auringon ja Maapallon massoille lausekkeet

m_A=\dfrac{4 \pi^2 r_M^3}{\gamma T_M^2}

m ​ A ​ ​ = \frac{​ 4 π ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ γ T ​ M ​ 2 ​ ​ ​}

m_M=\dfrac{4 \pi^2 r_K^3}{\gamma T_K^2}

m ​ M ​ ​ = \frac{​ 4 π ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​ ​}{​ γ T ​ K ​ 2 ​ ​ ​}

Lasketaan Auringon ja Maapallon massojen suhde.

\dfrac{m_A}{m_M}=\dfrac{4 \pi^2 r_M^3}{\gamma T_M^2} : \dfrac{4 \pi^2 r_K^3}{\gamma T_K^2}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ 4 π ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ γ T ​ M ​ 2 ​ ​ ​} : \frac{​ 4 π ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​ ​}{​ γ T ​ K ​ 2 ​ ​ ​}

\dfrac{m_A}{m_M}=\dfrac{4 \pi^2 r_M^3}{\gamma T_M^2} \cdot \dfrac{\gamma T_K^2}{4 \pi^2 r_K^3}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ 4 π ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ γ T ​ M ​ 2 ​ ​ ​} \cdot \frac{​ γ T ​ K ​ 2 ​ ​ ​ ​}{​ 4 π ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​}

\dfrac{m_A}{m_M}=\dfrac{ T_K^2 r_M^3 }{ T_M^2 r_K^3}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ T ​ K ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ T ​ M ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​}

\dfrac{m_A}{m_M}=\dfrac{ (27,3 \text{ d})^2 \cdot (21 \ 000R)^3 }{(365 \text{ d})^2 \cdot (60 R)^3}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ ( 2 7 , 3 d ) ​ 2 ​ ​ \cdot ( 2 1 0 0 0 R ) ​ 3 ​ ​ ​ ​}{​ ( 3 6 5 d ) ​ 2 ​ ​ \cdot ( 6 0 R ) ​ 3 ​ ​ ​}

Sijoitetaan lukuarvot

\approx 240 \ 000

\approx 240000

Vastaus

Auringon massa on noin 240 000 -kertainen Maan massaan verrattuna.

Fysiikan ylioppilaskoe S2008

Ratkaisu

Kirjataan lähtöarvot

m_k=5,2 \text{ kg}, \ m_t = 1,2 \text{ kg}

m ​ k ​ ​ = 5, 2 k g, m ​ t ​ ​ = 1, 2 k g

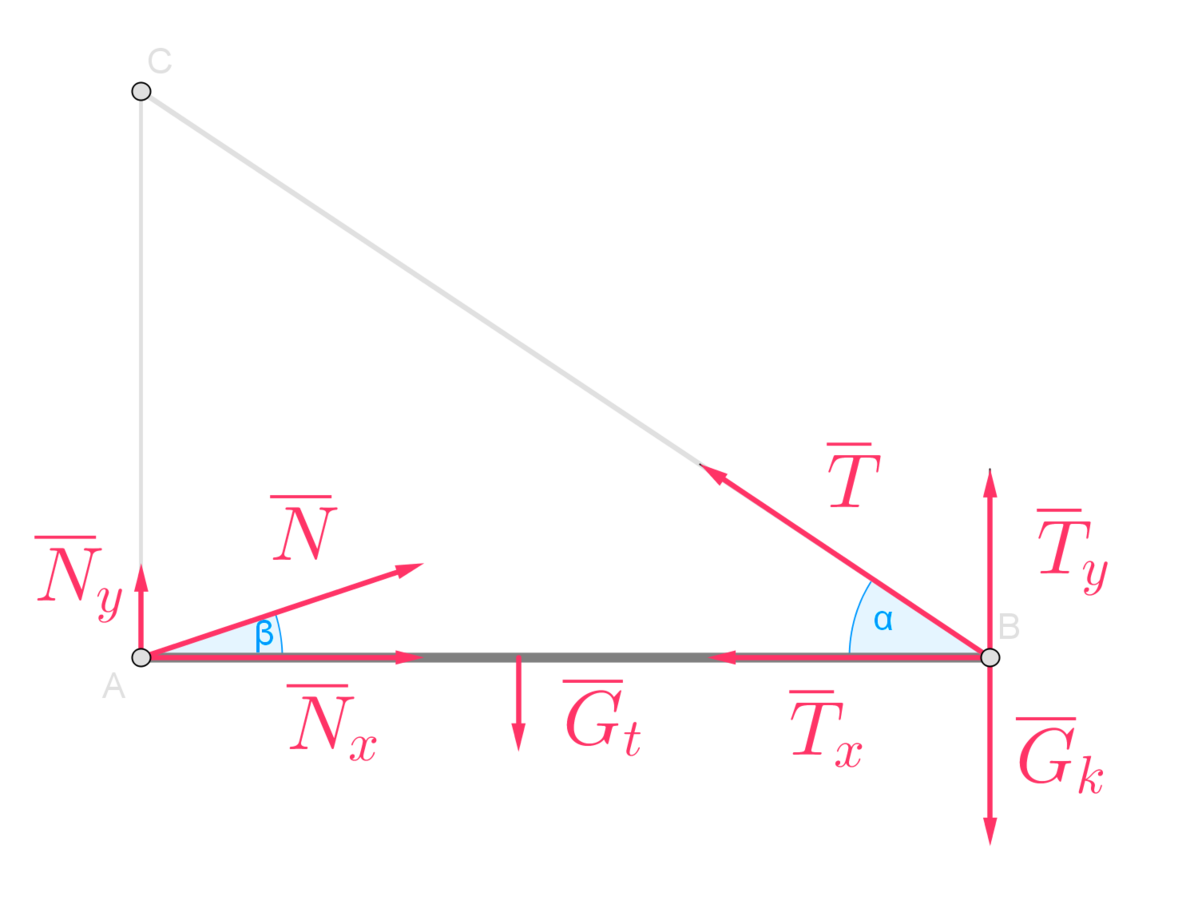
Piirretään tangon voimakuvio.

Tanko on tasapainossa etenemisen ja pyörimisen suhteen.

\text{NII } \sum \overline{F}=\overline{0}

N I I \sum ​ F ​ ​ ​ = ​ 0 ​ ​ ​

\sum M_A=0

\sum M ​ A ​ ​ = 0

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

h=0,42 \text{ m}, l=0,65 \text{ m}

h = 0, 42 m, l = 0, 65 m

Ratkaistaan kulma

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

\tan \color{CornflowerBlue}\alpha=\dfrac{0,42 \text{ m}}{0,65 \text{ m}}

tan α = \frac{​ 0 , 4 2 m ​ ​}{​ 0 , 6 5 m ​}

\color{CornflowerBlue}\alpha

α

\color{CornflowerBlue}\alpha \approx 32,869^\circ

α \approx 32, 86 9 ​ \circ ​ ​

\sum M_A=0

\sum M ​ A ​ ​ = 0

0,42 \text{ m}

0, 42 m

-G_t \dfrac{l}{2} - G_k l +T_y l=0

- G ​ t ​ ​ \frac{​ l ​ ​}{​ 2 ​} - G ​ k ​ ​ l + T ​ y ​ ​ l = 0

T_y l=G_t \dfrac{l}{2} + G_k l

T ​ y ​ ​ l = G ​ t ​ ​ \frac{​ l ​ ​}{​ 2 ​} + G ​ k ​ ​ l

T_y =\dfrac{1}{2}G_t + G_k

T ​ y ​ ​ = \frac{​ 1 ​ ​}{​ 2 ​} G ​ t ​ ​ + G ​ k ​ ​

T \sin \color{CornflowerBlue} \alpha =\dfrac{1}{2}G_t + G_k

T sin α = \frac{​ 1 ​ ​}{​ 2 ​} G ​ t ​ ​ + G ​ k ​ ​

0,65 \text{ m}

0, 65 m

T=\dfrac{\frac{1}{2}G_t + G_k}{\sin \color{CornflowerBlue}\alpha}

T = \frac{​ \frac{​ 1 ​ ​}{​ 2 ​} G ​ t ​ ​ + G ​ k ​ ​ ​ ​}{​ sin α ​}

:\sin \alpha

: sin α

: l

T_y=T \sin \alpha

T ​ y ​ ​ = T sin α

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

T=\dfrac{\frac{1}{2}G_t + G_k}{\sin \color{CornflowerBlue}\alpha}

T = \frac{​ \frac{​ 1 ​ ​}{​ 2 ​} G ​ t ​ ​ + G ​ k ​ ​ ​ ​}{​ sin α ​}

Lasketaan vaijerin jännitysvoiman suuruus.

T=\dfrac{\frac{1}{2}\cdot 1,2 \text{ kg} \cdot 9,81 \text{ m/s}^2 + 5,2 \text{6 kg} \cdot 9,81 \text{ m/s}^2}{\sin 32,869^\circ}

T = \frac{​ \frac{​ 1 ​ ​}{​ 2 ​} \cdot 1 , 2 k g \cdot 9 , 8 1 m / s ​ 2 ​ ​ + 5 , 2 6 k g \cdot 9 , 8 1 m / s ​ 2 ​ ​ ​ ​}{​ sin 3 2 , 8 6 9 ​ \circ ​ ​ ​}

T \approx 100 \text{ N}

T \approx 100 N

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

Tehdään voimatarkastelu x- ja y-suunnissa erikseen.

\sum \overline{F}_x=\overline{0}

\sum ​ F ​ ​ ​ ​ x ​ ​ = ​ 0 ​ ​ ​

\overline{N}_x+\overline{T}_x=\overline{0}

​ N ​ ​ ​ ​ x ​ ​ + ​ T ​ ​ ​ ​ x ​ ​ = ​ 0 ​ ​ ​

N_x - T_x =0

N ​ x ​ ​ - T ​ x ​ ​ = 0

N_x =T_x

N ​ x ​ ​ = T ​ x ​ ​

N_x =T \cos \color{CornflowerBlue}\alpha

N ​ x ​ ​ = T cos α

Sovitaan suunnat ylös ja oikealle positiivisiksi.

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

\sum \overline{F}_y=\overline{0}

\sum ​ F ​ ​ ​ ​ y ​ ​ = ​ 0 ​ ​ ​

\overline{N}_y+\overline{T}_y+\overline{G}_t+\overline{G}_k=\overline{0}

​ N ​ ​ ​ ​ y ​ ​ + ​ T ​ ​ ​ ​ y ​ ​ + ​ G ​ ​ ​ ​ t ​ ​ + ​ G ​ ​ ​ ​ k ​ ​ = ​ 0 ​ ​ ​

N_y +T_y -G_t-G_k =0

N ​ y ​ ​ + T ​ y ​ ​ - G ​ t ​ ​ - G ​ k ​ ​ = 0

N_y=G_t +G_k - T_y

N ​ y ​ ​ = G ​ t ​ ​ + G ​ k ​ ​ - T ​ y ​ ​

N_y=G_t +G_k - T \sin \color{CornflowerBlue}\alpha

N ​ y ​ ​ = G ​ t ​ ​ + G ​ k ​ ​ - T sin α

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

N_y=1,2 \text{ kg} \cdot 9,81 \text{ m/s}^2+5,2 \text{ kg} \cdot 9,81 \text{m/s}^2 - 104,84 \text{ N} \cdot \sin 32,869^\circ

N ​ y ​ ​ = 1, 2 k g \cdot 9, 81 m / s ​ 2 ​ ​ + 5, 2 k g \cdot 9, 81 m / s ​ 2 ​ ​ - 104, 84 N \cdot sin 32, 86 9 ​ \circ ​ ​

Lasketaan seinän tukivoiman x- ja y-suuntaisten komponenttien suuruudet.

N_y=G_t +G_k - T \sin \color{CornflowerBlue}\alpha

N ​ y ​ ​ = G ​ t ​ ​ + G ​ k ​ ​ - T sin α

N_y \approx 5,89\text{ N}

N ​ y ​ ​ \approx 5, 89 N

N_x =T \cos \color{CornflowerBlue}\alpha

N ​ x ​ ​ = T cos α

N_x =104,84 \text{ N} \cdot \sin 32,869^{\circ}

N ​ x ​ ​ = 104, 84 N \cdot sin 32, 86 9 ​ \circ ​ ​

N_x \approx 88,1 \text{ N}

N ​ x ​ ​ \approx 88, 1 N

0,42 \text{ m}

0, 42 m

0,65 \text{ m}

0, 65 m

Lasketaan Pythagoraan lauseen avulla seinän tukivoiman suuruus.

N=\sqrt{N_x^2+N_y^2}

N = \sqrt ​ N ​ x ​ 2 ​ ​ + N ​ y ​ 2 ​ ​ ​ ​ ​

N=\sqrt{(88,1 \text{ N})^2+(5,89 \text{ N})^2}

N = \sqrt ​ (88, 1 N) ​ 2 ​ ​ + (5, 89 N) ​ 2 ​ ​ ​ ​ ​

N \approx 88 \text{ N}

N \approx 88 N

Lasketaan tangentin avulla seinän tukivoiman suunta.

\tan \color{CornflowerBlue}\beta = \dfrac{N_y}{N_x}

tan β = \frac{​ N ​ y ​ ​ ​ ​}{​ N ​ x ​ ​ ​}

\tan \color{CornflowerBlue}\beta = \dfrac{5,89 \text{ N}}{88,1 \text{ N}}

tan β = \frac{​ 5 , 8 9 N ​ ​}{​ 8 8 , 1 N ​}

\color{CornflowerBlue}\beta \approx 3,8^\circ

β \approx 3, 8 ​ \circ ​ ​

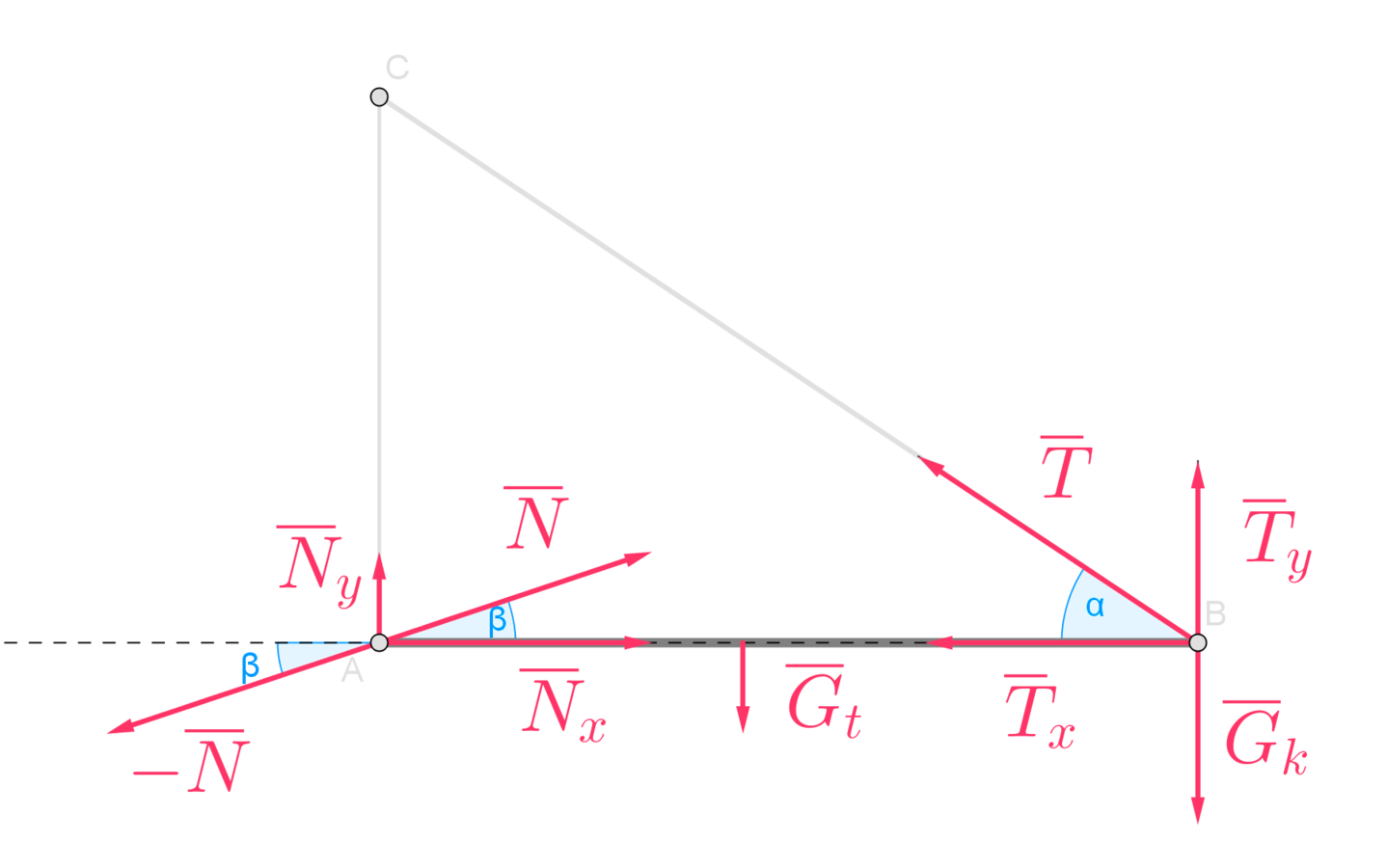
Newtonin 3. lain mukaan seinän tankoon kohdistama tukivoima on yhtä suuri kuin tangon seinään kohdistama voima, mutta vastakkaisuuntainen.

Vastaus:

Vaijerin jännitysvoiman suuruus on noin 100 N. Seinään kohdistuvan voiman suuruus on noin 88 N ja suunta poikkeaa seinän normaalista noin 3,8 astetta.

Fysiikan ylioppilaskoe S2011

Ratkaisu a-kohtaan

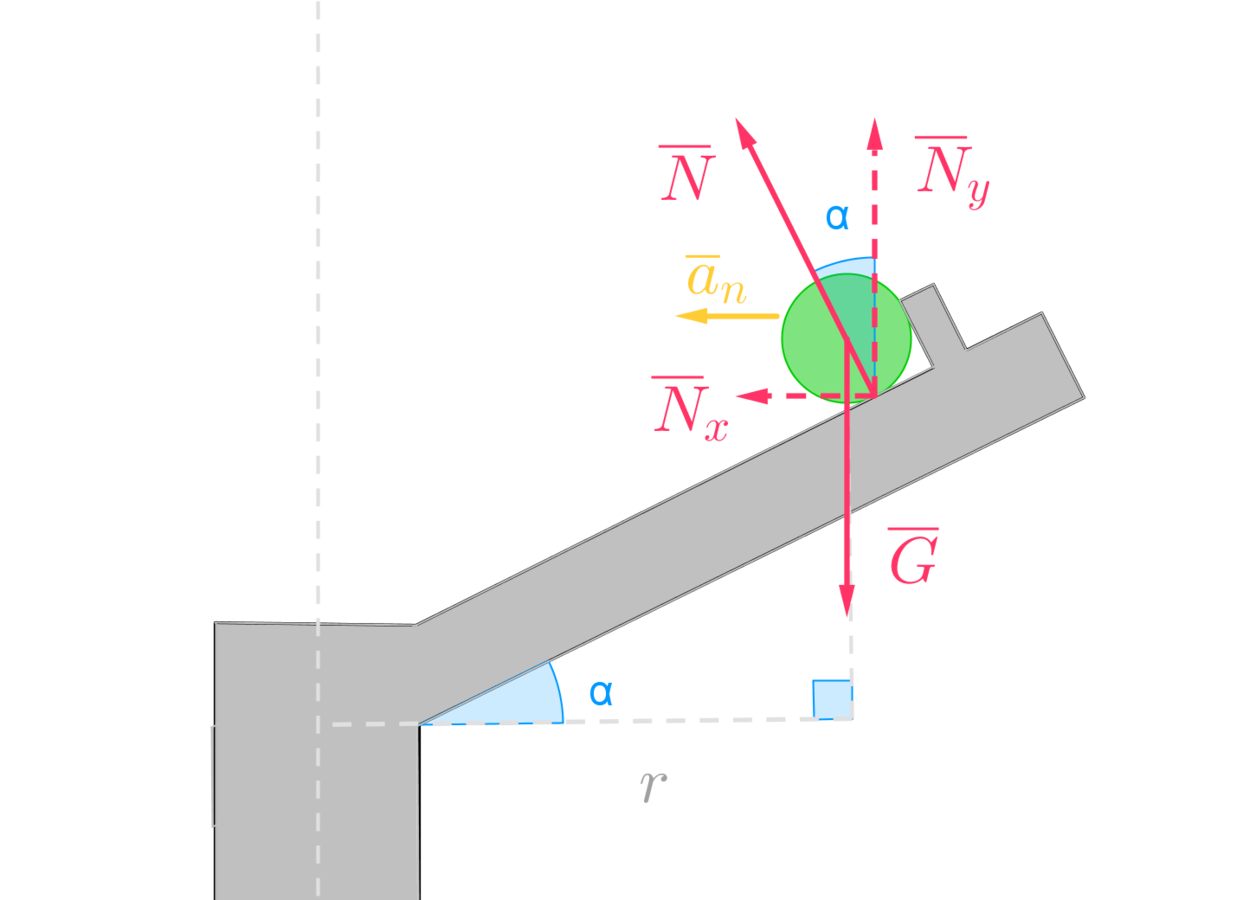
Piirretään teräskuulan voimakuvio.

Kun kuula on irronnut tapista, niin kuulaan vaikuttaa ainoastaan pinnan tukivoima ja paino.

(Kitka jätetään huomioimatta)

Ratkaisu b-kohtaan

Kirjataan lähtöarvot

\color{CornflowerBlue}\alpha=25^{\circ}

α = 2 5 ​ \circ ​ ​

r=0,32 \text{ m}

r = 0, 32 m

Oletetaan, että kuula on tasaisessa ympyräliikkeessä

Newtonin 2. lain mukaan

\sum \overline{F}=m\color{Goldenrod}{\overline{a}_n}

\sum ​ F ​ ​ ​ = m ​ a ​ ​ ​ ​ n ​ ​

Jaetaan voimatarkastelu x- ja y-suuntiin.

\sum \overline{F}_y=\overline{0}

\sum ​ F ​ ​ ​ ​ y ​ ​ = ​ 0 ​ ​ ​

\color{Salmon}{\overline{N}_y}+\color{Salmon}{\overline{G}}=\overline{0}

​ N ​ ​ ​ ​ y ​ ​ + ​ G ​ ​ ​ = ​ 0 ​ ​ ​

\color{Salmon}{N_y} = \color{Salmon}G

N ​ y ​ ​ = G

\color{Salmon}N \cos \color{CornflowerBlue}\alpha = \color{Salmon}G

N cos α = G

\color{Salmon}N \cos \color{CornflowerBlue}\alpha =\color{Salmon} G

N cos α = G

\color{Salmon}N = \dfrac{mg}{\cos \color{CornflowerBlue}\alpha}

N = \frac{​ m g ​ ​}{​ cos α ​}

\sum \overline{F}_x=m\color{Goldenrod}{\overline{a}_n}

\sum ​ F ​ ​ ​ ​ x ​ ​ = m ​ a ​ ​ ​ ​ n ​ ​

\color{Salmon}{\overline{N}_x}=m\color{Goldenrod}{\overline{a}_n}

​ N ​ ​ ​ ​ x ​ ​ = m ​ a ​ ​ ​ ​ n ​ ​

\color{Salmon}N \sin \color{CornflowerBlue}\alpha=m\dfrac{v^2}{r}

N sin α = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

a_n = \dfrac{v^2}{r}

a ​ n ​ ​ = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

N = \dfrac{mg}{\cos \alpha}

N = \frac{​ m g ​ ​}{​ cos α ​}

\dfrac{mg}{\cos \color{CornflowerBlue}\alpha} \sin \color{CornflowerBlue}\alpha=m\dfrac{v^2}{r}

\frac{​ m g ​ ​}{​ cos α ​} sin α = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

mg \tan\color{CornflowerBlue}\alpha=m\dfrac{v^2}{r}

m g tan α = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

mg \tan\color{CornflowerBlue}\alpha=m\dfrac{v^2}{r}

m g tan α = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

: m

g \tan\color{CornflowerBlue}\alpha=\dfrac{v^2}{r}

g tan α = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\cdot r

\cdot r

g r\tan\color{CornflowerBlue}\alpha=v^2

g r tan α = v ​ 2 ​ ​

v=\sqrt{g r\tan\color{CornflowerBlue}\alpha}

v = \sqrt ​ g r tan α ​ ​ ​

v=\sqrt{g r\tan\color{CornflowerBlue}\alpha}

v = \sqrt ​ g r tan α ​ ​ ​

Sijoitetaan lukuarvot

v=\sqrt{9,81 \text{ m/s}^2 \cdot 0,32 \text{ m}\cdot \tan 25^{\circ}}

v = \sqrt ​ 9, 81 m / s ​ 2 ​ ​ \cdot 0, 32 m \cdot tan 2 5 ​ \circ ​ ​ ​ ​ ​

v \approx 1,2099 \text{ m/s}

v \approx 1, 2099 m / s

Ratkaistaan kulmanopeus

v=\omega r, \text{ josta } \omega=\dfrac{v}{r}

v = ω r, j o s t a ω = \frac{​ v ​ ​}{​ r ​}

\omega = \dfrac{1,2099 \text{ m/s}}{0,32 \text{ m}}

ω = \frac{​ 1 , 2 0 9 9 m / s ​ ​}{​ 0 , 3 2 m ​}

\approx 3,8 \text{ rad/s}

\approx 3, 8 r a d / s

Vastaus:

Irtoamishetkellä kulmanopeus on noin 3,8 rad/s.

Fysiikan ylioppilaskoe K2008

Fysiikan ylioppilaskoe S2006

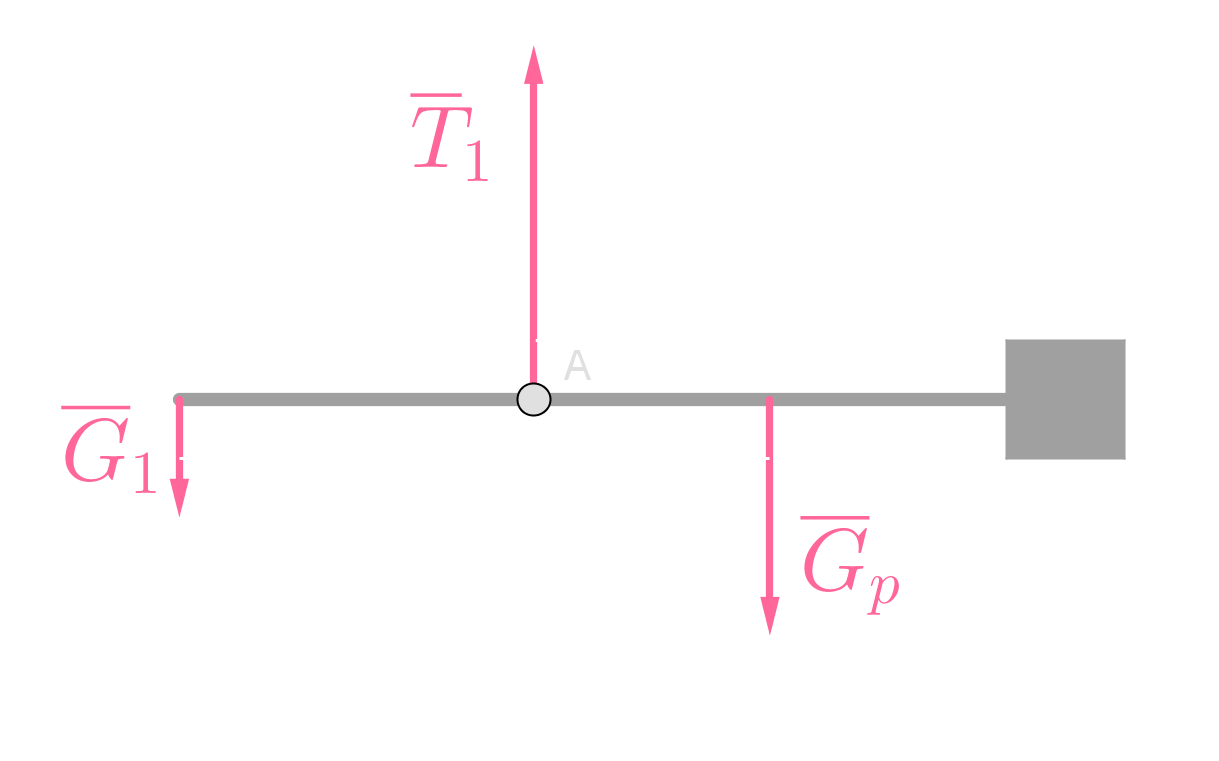
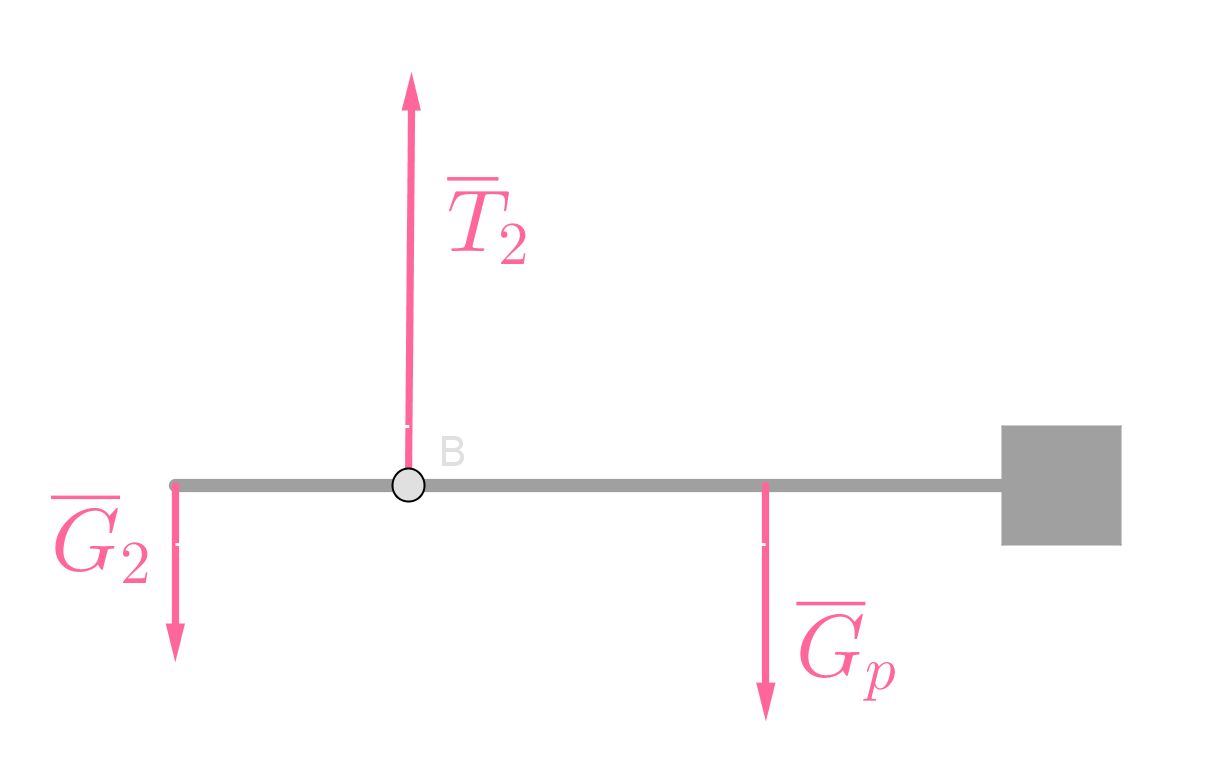
Ratkaisu

Kirjataan lähtöarvot

m_1=1 \text{ kg}, \ x_1=0,32 \text{ m}

m ​ 1 ​ ​ = 1 k g, x ​ 1 ​ ​ = 0, 32 m

m_2=2 \text{ kg}, \ x_2=?

m ​ 2 ​ ​ = 2 k g, x ​ 2 ​ ​ = ?

Piirretään voimakuviot tilanteista.

x_1-x_2 = 0,09 \text{ m}

x ​ 1 ​ ​ - x ​ 2 ​ ​ = 0, 09 m

1 kg:n ja 2 kg:n merkkien välimatka on 9,0 cm.

x_2 = x_1-0,09 \text{ m}

x ​ 2 ​ ​ = x ​ 1 ​ ​ - 0, 09 m

x_2 =0,32 \text{ m}-0,09 \text{ m}

x ​ 2 ​ ​ = 0, 32 m - 0, 09 m

x_2 =0,23 \text{ m}

x ​ 2 ​ ​ = 0, 23 m

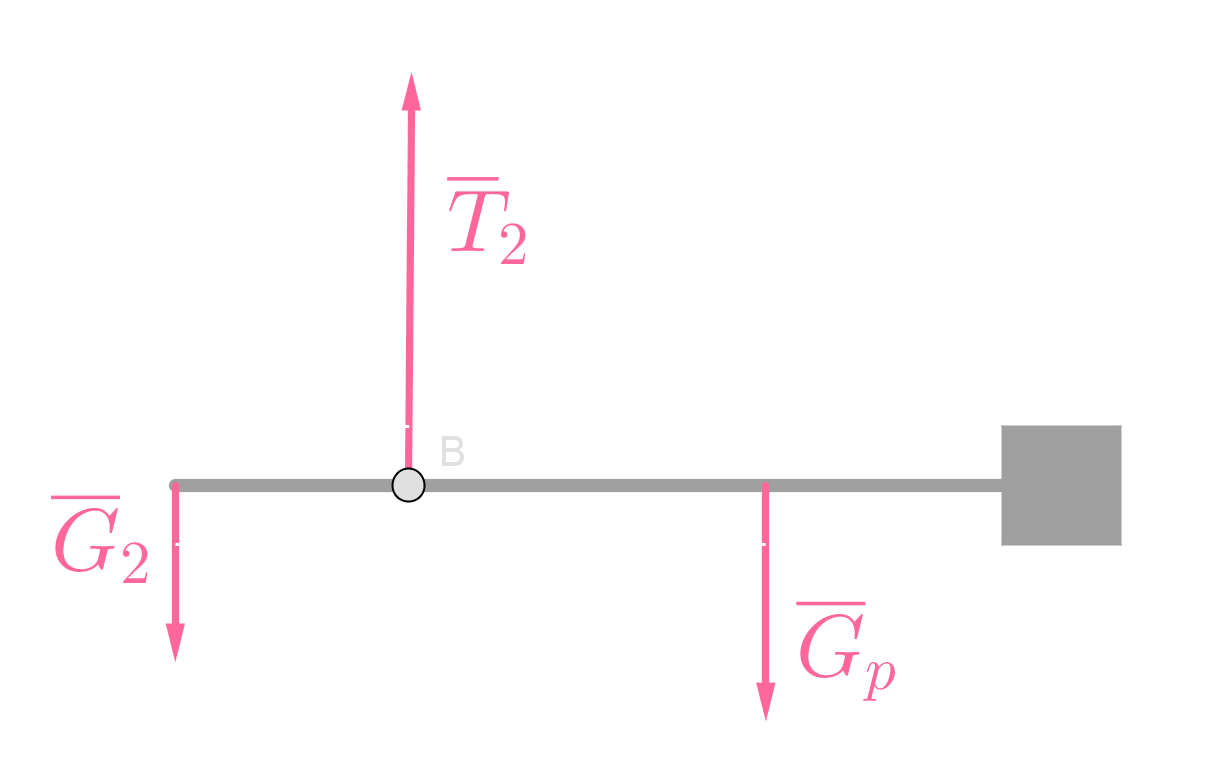
Kalavaaka on tasapainossa pyörimisen suhteen molemmissa tilanteissa.

\sum M_A = 0

\sum M ​ A ​ ​ = 0

\color{Salmon}{G_1} x_1 - \color{Salmon}{G_p}(r-x_1)=0

G ​ 1 ​ ​ x ​ 1 ​ ​ - G ​ p ​ ​ (r - x ​ 1 ​ ​) = 0

\sum M_B = 0

\sum M ​ B ​ ​ = 0

\color{Salmon}{G_2} x_2 - \color{Salmon}{G_p}(r-x_2)=0

G ​ 2 ​ ​ x ​ 2 ​ ​ - G ​ p ​ ​ (r - x ​ 2 ​ ​) = 0

\color{Salmon}{G_1} x_1 =\color{Salmon}{G_p}(r-x_1)

G ​ 1 ​ ​ x ​ 1 ​ ​ = G ​ p ​ ​ (r - x ​ 1 ​ ​)

\color{Salmon}{G_p}=\dfrac{ x_1 }{r-x_1}\color{Salmon}{G_1}

G ​ p ​ ​ = \frac{​ x ​ 1 ​ ​ ​ ​}{​ r - x ​ 1 ​ ​ ​} G ​ 1 ​ ​

\color{Salmon}{G_2} x_2 =\color{Salmon}{G_p}(r-x_2)

G ​ 2 ​ ​ x ​ 2 ​ ​ = G ​ p ​ ​ (r - x ​ 2 ​ ​)

\color{Salmon}{G_p}=\dfrac{ x_2 }{r-x_2}\color{Salmon}{G_2}

G ​ p ​ ​ = \frac{​ x ​ 2 ​ ​ ​ ​}{​ r - x ​ 2 ​ ​ ​} G ​ 2 ​ ​

Kalavaa'an paino saatiin esitettyä kahdella tavalla, joten muodostetaan näistä yhtälö.

\color{Salmon}{G_p}=\dfrac{ x_1 }{r-x_1}\color{Salmon}{G_1}

G ​ p ​ ​ = \frac{​ x ​ 1 ​ ​ ​ ​}{​ r - x ​ 1 ​ ​ ​} G ​ 1 ​ ​

\color{Salmon}{G_p}=\dfrac{ x_2 }{r-x_2}\color{Salmon}{G_2}

G ​ p ​ ​ = \frac{​ x ​ 2 ​ ​ ​ ​}{​ r - x ​ 2 ​ ​ ​} G ​ 2 ​ ​

\dfrac{ x_1 }{r-x_1}\color{Salmon}{G_1}=\dfrac{ x_2 }{r-x_2}\color{Salmon}{G_2}

\frac{​ x ​ 1 ​ ​ ​ ​}{​ r - x ​ 1 ​ ​ ​} G ​ 1 ​ ​ = \frac{​ x ​ 2 ​ ​ ​ ​}{​ r - x ​ 2 ​ ​ ​} G ​ 2 ​ ​

\dfrac{ x_1 }{r-x_1}m_1g=\dfrac{ x_2 }{r-x_2}m_2g

\frac{​ x ​ 1 ​ ​ ​ ​}{​ r - x ​ 1 ​ ​ ​} m ​ 1 ​ ​ g = \frac{​ x ​ 2 ​ ​ ​ ​}{​ r - x ​ 2 ​ ​ ​} m ​ 2 ​ ​ g

\dfrac{ x_1 }{r-x_1}m_1=\dfrac{ x_2 }{r-x_2}m_2

\frac{​ x ​ 1 ​ ​ ​ ​}{​ r - x ​ 1 ​ ​ ​} m ​ 1 ​ ​ = \frac{​ x ​ 2 ​ ​ ​ ​}{​ r - x ​ 2 ​ ​ ​} m ​ 2 ​ ​

m_1x_1(r-x_2)=m_2x_2(r-x_1)

m ​ 1 ​ ​ x ​ 1 ​ ​ (r - x ​ 2 ​ ​) = m ​ 2 ​ ​ x ​ 2 ​ ​ (r - x ​ 1 ​ ​)

G=mg

G = m g

: g

\cdot(r-x_1)(r-x_2)

\cdot (r - x ​ 1 ​ ​) (r - x ​ 2 ​ ​)

m_1x_1(r-x_2)=m_2x_2(r-x_1)

m ​ 1 ​ ​ x ​ 1 ​ ​ (r - x ​ 2 ​ ​) = m ​ 2 ​ ​ x ​ 2 ​ ​ (r - x ​ 1 ​ ​)

m_1x_1r-m_1x_1x_2=m_2x_2r-m_2x_1x_2

m ​ 1 ​ ​ x ​ 1 ​ ​ r - m ​ 1 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​ = m ​ 2 ​ ​ x ​ 2 ​ ​ r - m ​ 2 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​

m_1x_1r-m_2x_2r=m_1x_1x_2-m_2x_1x_2

m ​ 1 ​ ​ x ​ 1 ​ ​ r - m ​ 2 ​ ​ x ​ 2 ​ ​ r = m ​ 1 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​ - m ​ 2 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​

r(m_1x_1-m_2x_2)=m_1x_1x_2-m_2x_1x_2

r (m ​ 1 ​ ​ x ​ 1 ​ ​ - m ​ 2 ​ ​ x ​ 2 ​ ​) = m ​ 1 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​ - m ​ 2 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​

r=\dfrac{m_1x_1x_2-m_2x_1x_2}{m_1x_1-m_2x_2}

r = \frac{​ m ​ 1 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​ - m ​ 2 ​ ​ x ​ 1 ​ ​ x ​ 2 ​ ​ ​ ​}{​ m ​ 1 ​ ​ x ​ 1 ​ ​ - m ​ 2 ​ ​ x ​ 2 ​ ​ ​}

:(m_1x_1-m_2x_2)

: (m ​ 1 ​ ​ x ​ 1 ​ ​ - m ​ 2 ​ ​ x ​ 2 ​ ​)

Sijoitetaan lukuarvot

r=\dfrac{0,32 \text{ m} \cdot 0,23 \text{ m}(1 \text{ kg} -2 \text{ kg})}{1 \text{ kg} \cdot 0,32 \text{ m}-2 \text{ kg} \cdot 0,23 \text{ m}}

r = \frac{​ 0 , 3 2 m \cdot 0 , 2 3 m ( 1 k g - 2 k g ) ​ ​}{​ 1 k g \cdot 0 , 3 2 m - 2 k g \cdot 0 , 2 3 m ​}

r=\dfrac{x_1x_2(m_1-m_2)}{m_1x_1-m_2x_2}

r = \frac{​ x ​ 1 ​ ​ x ​ 2 ​ ​ ( m ​ 1 ​ ​ - m ​ 2 ​ ​ ) ​ ​}{​ m ​ 1 ​ ​ x ​ 1 ​ ​ - m ​ 2 ​ ​ x ​ 2 ​ ​ ​}

\approx 0,53 \text{ m}

\approx 0, 53 m