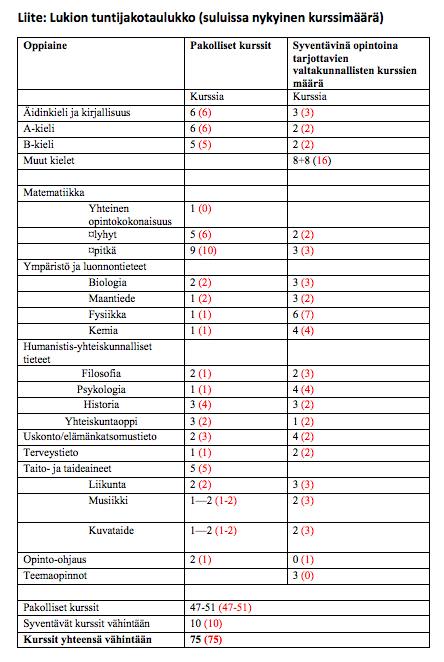
Tuntijako

linkki

LOPS2016 

Yleinen osa tiivistettynä 1/4

Oppimista edistetään ohjaamalla ja kannustamalla

Lukio-opinnoissa opiskelijoita ohjataan havaitsemaan käsitteiden, tiedonalojen ja osaamisen välisiä yhteyksiä sekä soveltamaan aiemmin oppimaansa muuttuvissa tilanteissa. Opintoihin liittyvät onnistumiset ja muut myönteiset kokemukset edistävät oppimista ja innostavat osaamisen kehittämiseen.

Ohjaava arviointi tukee oppimista

Arvioinnin tehtävänä on edistää oppimista. Lähtökohtana on, että opiskelijat ymmärtävät, mitä heidän on tarkoitus oppia ja miten oppimista arvioidaan. Arvioinnilla opiskelijaa kannustetaan omien tavoitteiden asettamiseen ja tarkoituksenmukaisten työskentelytapojen valintaan. Jokaisen kurssin alussa opiskelija kanssa tulee käydä läpi kurssin tavoitteet ja arviointiperusteet.

LOPS2016 

Yleinen osa tiivistettynä 2/4

Opiskelijoita rohkaistaan osallistumaan

Yhteisellä suunnittelulla vahvistetaan sitoutumista yhdessä määriteltyihin tavoitteisiin ja toimintatapoihin. Lukiossa pyritään monipuoliseen vuorovaikutukseen lukion sisällä ja suhteessa ympäröivään yhteiskuntaan.

Lukio kasvattaa tulevaisuutta varten

Lukiokoulutuksen aikana opiskelija rakentaa identiteettiään, ihmiskäsitystään, maailmankuvaansa ja –katsomustaan sekä paikkaansa maailmassa. Samalla opiskelija kehittää suhdettaan menneisyyteen ja suuntautuu tulevaisuuteen. Lukiokoulutus ohjaa opiskelijaa tulevaisuuden suunnitelmien laadintaan ja elinikäiseen oppimiseen.

LOPS2016 

Yleinen osa tiivistettynä 3/4

Lukiokoulutus vahvistaa yleissivistystä

Lukio-opetuksessa yleissivistys koostuu arvoista, tiedoista, taidoista, asenteista ja tahdosta.  Lukiokoulutuksessa kriittiseen ja itsenäiseen ajatteluun kasvavat opiskelijat harjaantuvat toimimaan vastuullisesti, myötätuntoisesti, yhteisöllisesti ja menestyksekkäästi.

Lukio kehittää arvo-osaamista

Lukio-opetus kehittää arvo-osaamista käsittelemällä julkilausuttujen arvojen ja todellisuuden välisiä jännitteitä. Lukion arvoperusta toteutuu lukion toimintakulttuurissa. Toimintakulttuuri tulee näkyväksi yhteisön kaikessa toiminnassa ja sen jäsenten tavassa kohdata toinen toisensa. Aihekokonaisuudet ovat arvokannanottoja ajankohtaisiin kasvatus- ja koulutushaasteisiin.

LOPS2016 

Yleinen osa tiivistettynä 4/4

Opiskeluympäristöt tukevat monipuolista ja aktiivista työskentelyä sekä yhteistyötaitojen kehittymistä

Tavoitteena on, että opiskeluympäristöt ovat monipuolisia ja että ne rikastuttavat opiskeluun liittyviä kokemuksia ja edistävät opiskelumotivaatiota. Rakennettuja tiloja ja luontoa hyödynnetään opiskelussa siten, että luova ajattelu ja tutkimiseen perustuva opiskelu on mahdollista.

Matematiikan yhteinen opintokokonaisuus

Mahdollisuudet

Uhkakuvat

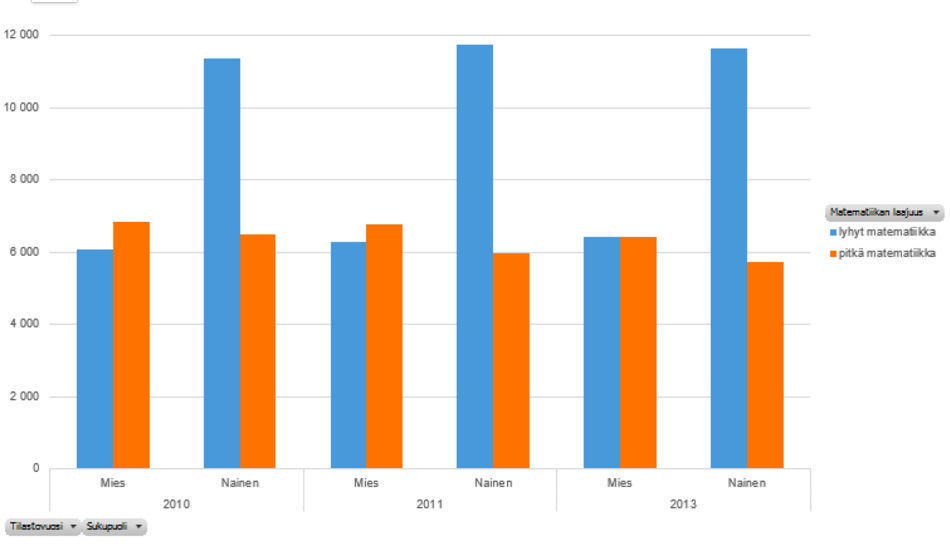
Lukion oppimäärän suorittaneista opiskelijoista pitkää ja lyhyttä matematiikkaa opiskelleet

Teknologiateollisuus ry

"Matematiikan yhteinen opintokokonaisuus (5.6.1)
Yksilöllistä tukea lukion matematiikan opintojen alkuvaiheessa tulee vahvistaa, jotta mahdollisimman moni opiskelija valitsisi pitkän matematiikan yhteisen opintokokonaisuuden jälkeen. Tuen tulisi rohkaista erityisesti tyttöjä valitsemaan pitkän matematiikan opinnot."

Kemianteollisuus ry

"Pitkän matematiikan suorittajien määrää tulee lukiossa lisätä. Huolenamme on, että työryhmän ehdottaman matematiikan yhteisen opintokokonaisuuden seurauksena entistä useampi päätyy valitsemaan matematiikan lyhyen oppimäärän. Erityisen tärkeää on, että lukion alussa niitä opiskelijoita, joilla on edellytykset suorittaa pitkä oppimäärä, myös kannustetaan valitsemaan ja suorittamaan pitkän matematiikan kurssit. Tyttöjen kannustamiseen ja rohkaisemiseen tulee kiinnittää erityistä huomiota. "

Millaiset ovat lukioon tulevan opiskelijan matemaattiset tiedot ja taidot? 

Matematiikan sisältötavoitteet vuosiluokilla 7 - 9

S1 Ajattelun taidot ja menetelmät:

looginen ajattelu, vaihtoehtojen lukumäärä, päättelykyky, matemaattisen tekstin tutlkitseminen ja tuottaminen, todistamisen perusteet, väitelauseet ja niiden totuusarvot, algoritminen ajattelu, ohjelmoidaan

S2 Luvut ja laskutoimitukset

peruslaskutoimitukset negatiivisilla luvuilla ja murtoluvuilla, vastaluku, käänteisluku, itseisarvo, reaaliluvut, jaollisuus, alkutekijät, desimaalilukujen laskutoimitukset, tarkka arvo, likiarvo, pyöristäminen, prosentti, prosenttiosuus, perusarvo, muuttunut arvo, muutos- ja vertailuprosentti, potenssilaskenta, neliöjuuri

Matematiikan sisältötavoitteet vuosiluokilla 7–9

S3 Algebra:

muuttuja, lauseke, lausekkeen arvo, sievennys, polynomi, polynomien laskutoimitukset, lausekkeiden muodostaminen ja sieventäminen, ensimmäisen asteen yhtälöt, vaillinaiset toisen asteen yhtälöt, ratkaisut graafisesti ja algebrallisesti, ensimmäisen asteen epäyhtälöt, lukujonot, verranto 

S4 Funktiot:

riippuvuudet graafisesti ja algebrallisesti, suoraan ja kääntäen verrannollisuus, funktio, suora, paraabeli, koordinaatisto, kulmakerroin, vakiotermi, funktion kasvaminen ja väheneminen, nollakohta. 

Matematiikan sisältötavoitteet vuosiluokilla 7-9

S5 Geometria:

piste, jana, suora, kulma, viiva, puolisuora ja näiden ominaisuudet, yhdenmuotoisuus, yhtenevyys, Pythagoraan lause ja sen käänteislause, trigonometriset funktiot, kehä- ja keskuskulma, Thaleen lause, piirit, pinta-alat, ympyrä, kaaren pituus, sektorin pinta-ala, kehän pituus, pallon lieriön ja kartion tilavuudet ja pinta-alat, mittayksiköt ja yksikkömuunnokset.

S6 Tietojen käsittely ja tilastot sekä todennäköisyys:

tiedon kerääminen, jäsentäminen ja analysoiminen, keskiarvo, tyyppiarvo, frekvenssi, suhteellinen frekvenssi, mediaani, hajonta, diagrammit, todennäköisyydet 

Matematiikan yhteinen oppimäärä

Matematiikan yhteisen opintokokonaisuuden tehtävänä on herättää opiskelijan kiinnostus matematiikkaa kohtaan muun muassa tutustuttamalla hänet matematiikan moninaiseen merkitykseen ihmiselle ja yhteiskunnalle ainutlaatuiseen ja kiehtovaan olemukseen tieteenalana. 

Tässä opintokokonaisuudessa opiskelijalla on tilaisuus vahvistaa pohjaa matematiikan opinnoilleen ja nähdä matematiikka hyödyllisenä ja käyttökelpoisena selitettäessä ja hallittaessa muun muassa yhteiskunnan, talouden ja luonnon tapahtumia ja tilanteita.

Kurssin tavoitteena on, että opiskelija 

• pohtii matematiikan merkitystä yksilön ja yhteiskunnan näkökulmasta

• kertaa ja täydentää lukualueet, kertaa peruslaskutoimitukset ja prosenttilaskennan periaatteet 

• vahvistaa ymmärrystään funktion käsitteestä

• ymmärtää lukujonon käsitteen

MAY1: Luvut ja lukujonot

Jatkuu...

MAY1: Luvut ja lukujonot

• osaa määrittää lukujonoja, kun annetaan alkuehdot ja tapa, jolla seuraavat termit muodostetaan.

• saa havainnollisen käsityksen lukujonon summan määrittämisestä.

• osaa ratkaista käytännön ongelmia aritmeettisen ja geometrisen jonon ja niistä muodostettujen summien avulla.

• osaa käyttää teknisiä apuvälineitä funktion kuvaajan ja lukujonojen tutkimisessa sekä lukujonoihin liittyvien sovellusongelmien ratkaisussa.

MAY1: Luvut ja lukujonot

Keskeiset sisällöt 

• reaaliluvut, peruslaskutoimitukset ja prosenttilaskenta

• funktio, kuvaajan piirto ja tulkinta 

• lukujono

• rekursiivinen lukujono

• aritmeettinen jono ja summa

• logaritmi ja potenssi sekä niiden välinen yhteys  muotoa                              olevien yhtälöiden ratkaiseminen 

• geometrinen jono ja summa 

Mikä on "Tuttua" ?

Keskeiset sisällöt 

• reaaliluvut, peruslaskutoimitukset ja prosenttilaskenta

• funktio, kuvaajan piirto ja tulkinta 

• lukujono

• rekursiivinen lukujono

• aritmeettinen jono ja summa

• logaritmi ja potenssi sekä niiden välinen yhteys  muotoa                              olevien yhtälöiden ratkaiseminen 

• geometrinen jono ja summa 

kysymyksiä, TASO 1

• Miten kurssi toteutetaan
  • isossa lukiossa?
  • pienessä lukiossa?
• "osaa käyttää teknisiä apuvälineitä funktion kuvaajan ja lukujonojen tutkimisessa sekä lukujonoihin liittyvien sovellusongelmien ratkaisussa." ?

kysymyksiä, TASO II

• Miten saadaan enemmän opiskelijoita innostettua pitkän matematiikan pariin?
• Miten kurssi arvioidaan niin, että lukiolaki ja LOPS toteutuvat?
• "Voiko lyhyen matematiikan opiskelija saada kiitettävää arvosanaa?"

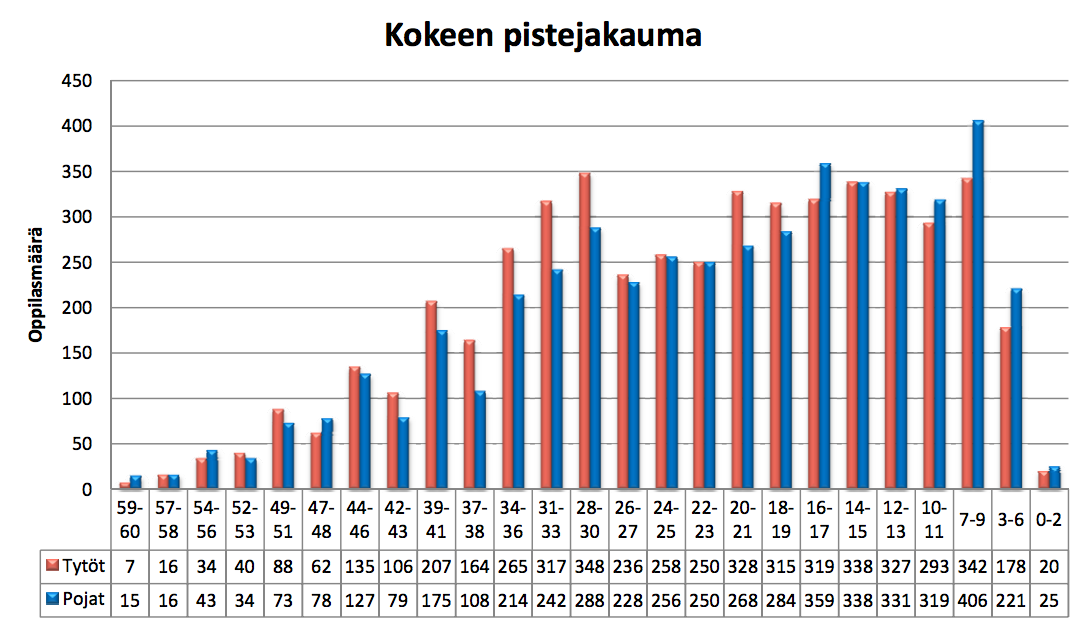
Valtakunnallinen 9. luokan matematiikan koe

kysymyksiä, TASO III

• Pystyykö kurssin opettamaan opettajakeskeisesti?
• S-merkintä? 

Lukion oppimäärän suorittaneista opiskelijoista pitkää ja lyhyttä matematiikkaa opiskelleet

vipunen