Learn how to play Atari games with AI

Who am I?
- Developer since 2000
- In Topdanmark since 2012
- IT-Skade
- Machine Learning
- Innovation Lab
The Machine Learning team
Disclaimer:
This presentation is not an introduction to deep learning!
Atari games!
3 eksempler på Atarispil
Hvordan spiller man et Atarispil? Deles op i frames, hvor man kan gå til højre, venstre etc.
Beskriv programmeringsvejen Niveau 1
Beskrive pixelvejen for eet spil - niveau 2
Beskrive pixelvejen i samme form for alle spil - niveau 3
Målet er ikke at spille perfekt, men at spille bedre end mennesker
(achieve super human performance)
But.. why?????
Why did Google pay +500 million $ for Deepmind?
The road to AGI...
Artificial General Intelligence
What is that???
"intelligence of a machine that could successfully perform any intellectual task that a human being can"
-
Learn features from samples
-
No more input than a human sees (pixels)
-
Learn new features in the same model and conserve the existing
-
Improve existing model
-
Reuse existing model
Overall goal of AGI is to:
Current state of AI:
"The intelligence in Artificial Intelligence lies within the team"
Danny Lange (I think) at Nordic AI 2017
Complex decisions are... complex!!!
Back to the Atari games...
Originally solved by Google DeepMind in 2013 to play 7 different games
Use the same algorithm and parameters to train different models to play Atari games
-
One model pr. game
-
Algorithm is the same for all games
-
Hyperparameters for the algorithm are the same for all games
Improved in 2015 to play 49 different games
A thing about deep learning...
How to play Atari games?
Play by observing the pixels on the screen
Estimate the future reward for each move
Based on the reward, decide which action to take
state = game.start()
pixels = state.getPixels()
rewards = model.predict(pixels)
bestAction = getBestActionFromRewards(rewards)
state = game.move(bestAction)
Algorithm in its simplest form
Pretty simple, right?
Using Reinforcement Learning
Reinforcement Learning is based on the principle of a reward
First problem:
Get Access to the Atari game "Breakout"
ALE + OpenAI Gym
Environment for playing multiple platform games
import gym
env = gym.make('BreakoutDeterministic-v0')
env.reset()
while True:
env.render()
# Random action
action = env.action_space.sample()
next_state, reward, is_done, info = env.step(action)
print("Reward: {}, is_done: {}".format(reward, is_done))
if is_done:
env.reset()A random Atari agent, playing forever
(erstat med pseudokode)
- Spil tilfældigt
- Forudse mulig belønning ved næste træk
- På baggrund af højeste belønning vælges næste træk
The algorithm used by DeepMind was named Deep Q-network (DQN)
What is Q?
Given state and action, predict Q and update the network with the Q value for that action
Imagine you have the ultimate function:
What is a state?




A state consists of 4 grayscaled images
The next state is this state with the next image attached at the end, and then the first image is removed
What is an action?
An action can be either
- 0 - do nothing
- 1- shoot
- 2 - right
- 3 - left
Given state and action, predict Q and update the network with the Q value for that action
Q(s,a) is the estimated reward for an action given a current state
Hvad er input til netværket?
Tegning af input
Next state (udgår)




(udgår)Each image is grayscaled, and resized to an array of 84 x 84 pixels
What is the output?
Tegning af output med Q(s,a) værdier
How do we train this?
-
Predict an action from the model
-
Make next move in the game with this action
-
Record the resulting state, action and score
-
Put that state into a memory containing up to 1 million elements
-
For each time we finish a game or reach a threshold, pick 32 states from memory
-
Calculate Q for each of these 32 states
-
Train the network with these 32 states and the Q value for them
-
Start a new game
- Let it play random
- Train network with sucess/failures
Let it play random
Tegning af hvad der sker ved et træk både random og model (input, state, output).
Gem state i memory, spil til man dør, træn batch med 32 elementer mod netværk, lav et nyt spil
Each time we take an action we record:
- Current state
- Action
- Reward
- Next state
- Did I die?
Train the network
For each state in the batch of 32 elements, calculate Q
- r = reward
- \(\gamma\) = discount
- Q(s', a') = prediction from model
Introducing principle of discounting future reward...
A thing about a stochastic environment:
- A complete game make up a defined set of states and actions. Hereby we get a total reward for a game
- Since it is stochastic, e.g. the next ball will start out randomly, we can never predict each game to be exactly the same, based on a specific set of actions
- We need to discount future rewards, due to this fact
- The longer into the future we estimate, the more it may diverge, and the less we may take it into consideration
Had it been deterministic, we could just have replayed an entire game, and always be sure to get the same result
- r = reward
- \(\gamma\) = discount
- Q(s', a') = prediction from model
\(\gamma\)
Gamma:
Set to 0.95 since we only predict 4 steps into the future - and that magically works!
Example:
- Q of next state is 0.7
- reward of current action is one
- discount (gamma) is 0.95
- action is 2 (right)
1 + 0.95 x (0.7) = 1.665
The network is trained with 1.665 put into the Q value of the current action and next state
[0.45][0.23][1.665][0.7664]
initialise Q(numstates,numactions) arbitrarily
observe initial state s
repeat
select and carry out an action a
observe reward r and new state s'
Q(s,a) = r + γ(max(Q(s',a')))
s = s'
until terminatedQ learning algorithm
We still miss the replay batch principle to make it work...
Deep Q-network
initialize replay memory D
initialize action-value function Q with random weights
observe initial state s
repeat
select an action a
with probability ε select a random action
otherwise select a = argmaxa’Q(s,a’)
carry out action a
observe reward r and new state s’
store experience <s, a, r, s’> in replay memory D
sample random transitions <ss, aa, rr, ss’> from replay memory D
calculate target for each minibatch transition
if ss’ is terminal state then tt = rr
otherwise tt = rr + γ (max(Q(ss’, aa’)))
// definition for back propagation
train the Q network using (tt - Q(ss, aa))^2 as loss
s = s'
until terminatedPerfect! Only problem is... it doesn't work!! :-(
A lot of tricks is used to actual make it work:
- Error clipping
- Reward clipping
- Gradient clipping
- Target network
- and som other tricks
All tricks with the goal of stabilising the network training
The actual neural network is 3 x convolutional network with a fully connected layer with 512 neurons
Convolution2D(32, 8, 8, subsample=(4, 4), input_shape=(84, 84, 4)))
Activation('relu')
Convolution2D(64, 4, 4, subsample=(2, 2))
Activation('relu')
Convolution2D(64, 3, 3, subsample=(1, 1))
Activation('relu')
Dense(512)
Activation('relu')
Dense(4) # Range of possible actions
Activation('linear')Pseudo code in Keras
Future of AI
Sources:
Terminology:
- Prediction: Ask the model for a result from data
- Network: The construct that calculates the model and is used to make predictions on data
- Model: The trained knowledge of how to make predictions for this specific problem
- Training: Feed categorised data into the network and ask it to produce a model that can map the input data to the expected result
- Error: How far the calculation was from the expected result is called the "error"
- Hyper parameters: Parameters used to calibrate the network for a specific problem
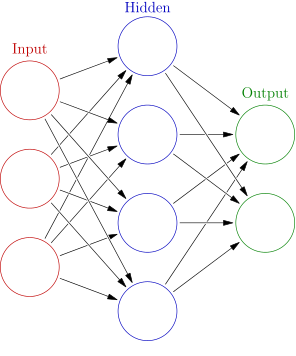
Artificial Neural Network
Originally an idea from late in the 1940's
Neural network
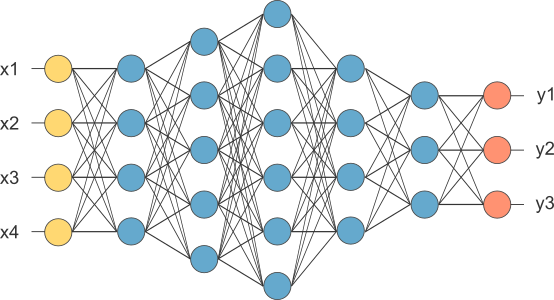
Deep Learning
Multilayered neural networks
Universal approximation algorithm
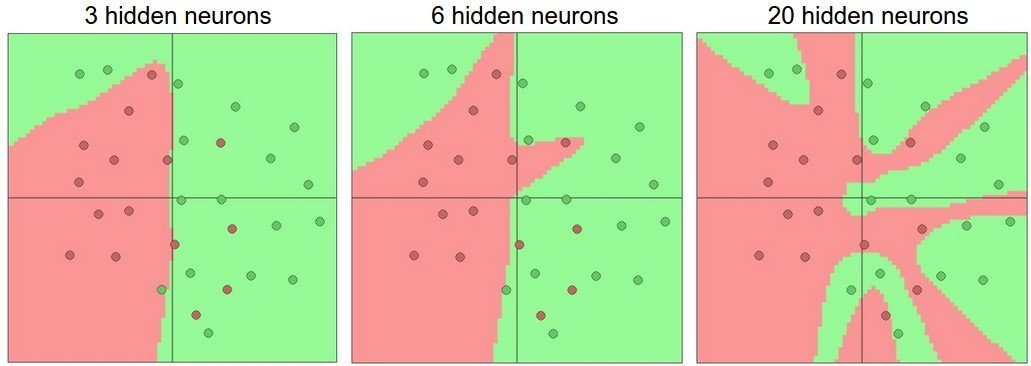
Neurons is the building blocks
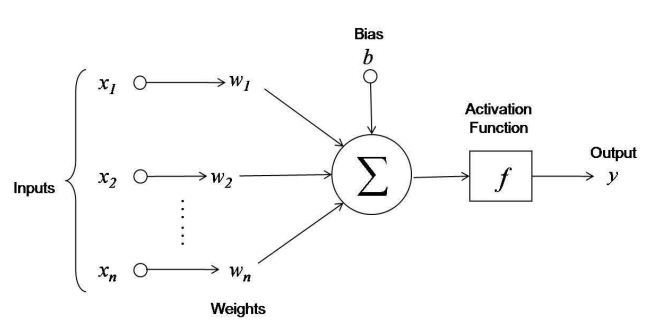
Great for image recognition and complex categorisation with large datasets
Is all good then???
Need LOTS of data!
Training takes long time
No defined approach for calibrating hyper parameters
Basically: Trial/Error
Goal is to minimise the error for a prediction
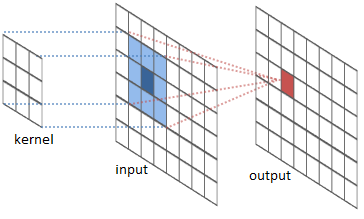
Convolutional networks
Used for image recognition