
Computational Biology

(BIOSC 1540)

Sep 5, 2024
Lecture 04:
De novo assembly
Announcements

We are putting our computer algorithm hats now
After today, you should be able to
1. Explain the fundamental challenge of reconstructing a complete genome.
2. Describe and apply the principles of the greedy algorithm.
3. Understand and construct de Bruijn graphs.

This is just alignment with extra steps
(our topic for next Thursday)
What is done 99% of the time


Repeats and high coverage are the main challenges

After today, you should be able to
1. Explain the fundamental challenge of reconstructing a complete genome.
2. Describe and apply the principles of the greedy algorithm.
3. Understand and construct de Bruijn graphs.
Let's formulate our problem
Suppose we have a collection of strings (i.e., reads)
(In CS, we call a sequence of characters a string)
BAA
AAB
BBA
ABA
ABB
BBB
AAA
BAB
We want to assemble these strings into a single, continuous string (i.e., contig)
What's the easiest way?
Concatenate
BAAAABBBAABAABBBBBAAABAB
Done!
Well, no.
Right?
This is called a "superstring"
Suppose we want the shortest superstring
This is a valid superstring, but why would we want the shortest?
BAAAABBBAABAABBBBBAAABAB

Talk with your neighbors
Overlap maximization
- Reduces redundancy
- Maximizes confidence with highest overlaps
Repeat resolution
Resolves repeats by favoring collapsed arrangements
Evolutionary pressure
Most genomes have selective pressure to be efficient
Merge strings by highest overlap
We can arrange the strings with overlaps of two
BAAAABBBAABAABBBBBAAABAB
Concatenated:
AAABBBABAA
Overlapped:
AA
AAA
B
AB
B
BB
B
BB
A
BA
B
AB
A
BA
A
Great! That was easy
- Merge strings one at a time keeping a consistent 5' and 3'
- Always merge the largest overlap
- Repeat

Procedure
What happens if we have a tie?

Talk with your neighbors


5
5
4,
4
4
Length = 9
Tie breakers are a personal preference
First encountered, first merged
Highest quality base calls
Highest coverage
Look ahead
Exclude
The one you found first
Use sequence with highest quality
Whichever results in more coverage
Do both and evaluate consequences
Be petty and don't merge them (separate contigs)
Being greedy makes genome assembly tractable
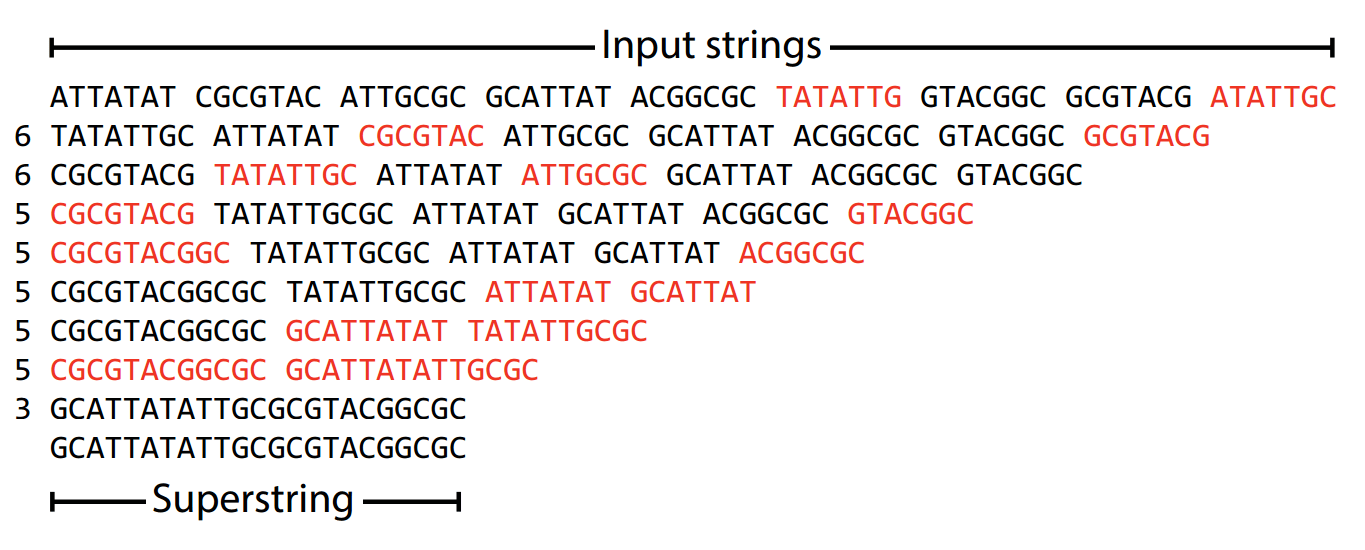

Let's get some practice being greedy
ABA
ABB
AAA
AAB
BBB
BBA
BAB
BAA

For ties, choose the one you found first
Repeats ruin our assembly
a_long_long_long_time
We are missing a "_long". Why?
Let's take a string, and cyclically permute it with k = 6

Longer reads and genome assembly
We get the correct string back, but how did increasing our k fix this?

a_long_long_long_time
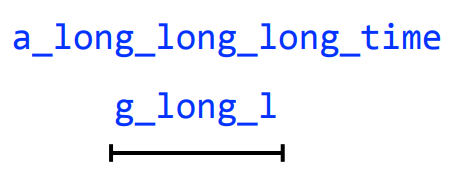
By having one read span all three "long"s, we prevented a collapse
k = 8

Greedy assembly is not used in practice
It just helps us understand our problem
After today, you should be able to
1. Explain the fundamental challenge of reconstructing a complete genome.
2. Describe and apply the principles of the greedy algorithm.
3. Understand and construct de Bruijn graphs.
Graphs is a data structure for drawing relationships between items
Node
Represents a single entity
- Person
- Location
- Protein
- Sequencing read
Edge
Represents a connection (possibly with a direction)
- Instagram follower
- Flights
- Protein-protein interaction
- Sequence overlap
Genome assembly uses direct edges to specify overlap and concatenation
"tomorrow and tomorrow and tomorrow"
Let's build a directed multigraph:
- Each unique k-mer is a node
- Add directed edges for each overlap and concatenation
K-mer is a substring of length k
(We will cheat here and write down just unique words)
tomorrow
and
Building k-mers from a string
GGCGATTCATCG
- Slice first k characters
- Shift right one character
- Repeat
Spectrum with k = 3
GGC
GCG
CGA
TCG
ATC
GAT
ATT
TTC
TCA
CAT
All 3-mers
Build a De Bruijn graph with k-1 nodes
AATGGCGTA
AAT
ATG
GGC
GCG
TGG
CGT
GTA
AATG
ATGG
TGGG
GGCG
GCGT
CGTA
5'
3'
Step 1:
Let's use k = 4
Step 2:
AATG
L
R
Repeat
ATGG
TGGG
GGCG
GCGT
CGTA
A node is balanced if indegree equals outdegree
Semi-balanced has difference of 1
Take left and right k-1 mer and make two connected nodes
Build k-mers
Graph is Eulerian if it contains <= 2 of these
De Bruijn practice
CGTAAAT

Build a De Bruijn graph with k = 3
CGT
GTA
TAA
AAA
AAT
CG
GT
TA
AA
AT
De Bruijn graphs with multiple reads
5' AATGGCGTA 3'
5' CGTAAAT 3'
Read 1
Read 2
Let's use k = 4
Wait, what happend? This is not Eulerian
Circular genomes are not Eulerian
AAT
ATG
GGC
GCG
TGG
CGT
GTA
TAA
AAA
Redo, but make it not circular
5' AATGGCGTA 3'
5' CGTAAAG 3'
5' TAAAGGCGAA3'
Read 1
Read 2
Read 3
AAT
ATG
GGC
GCG
TGG
CGT
GTA
TAA
AAA
AAG
CGA
GAA
AGG
Overlap
Edges on walk extend the contig
Why is this not Eulerian?
More than two semi-balanced nodes
Cannot walk along each edge once
We can add weights to edges
5' AATGGCGTA 3'
5' CGTAAAG 3'
5' TAAAGGCGAA3'
Read 1
Read 2
Read 3
Still not Eulerian, but we can walk it
If there was no overlap, then we would have some unconnected graphs
AAT
ATG
GGC
GCG
TGG
CGT
GTA
TAA
AAA
AAG
CGA
GAA
AGG
2
2
2
1
1
1
1
1
2
1
1
1
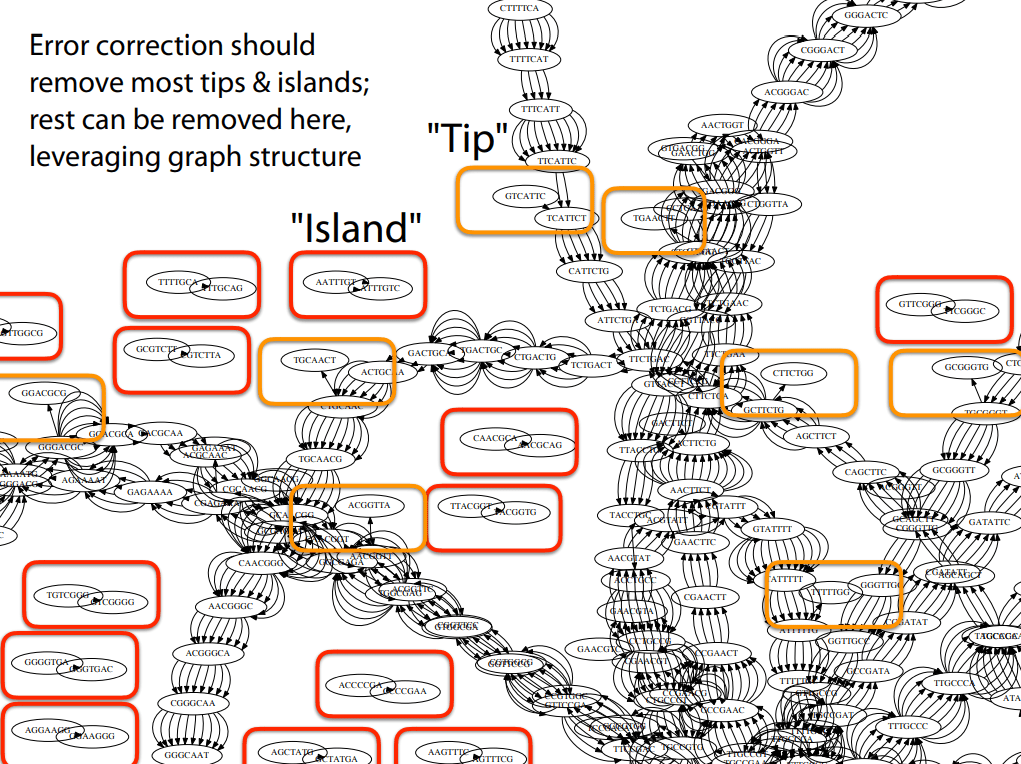
Errors dramatically increase the number of edges and unconnected graphs
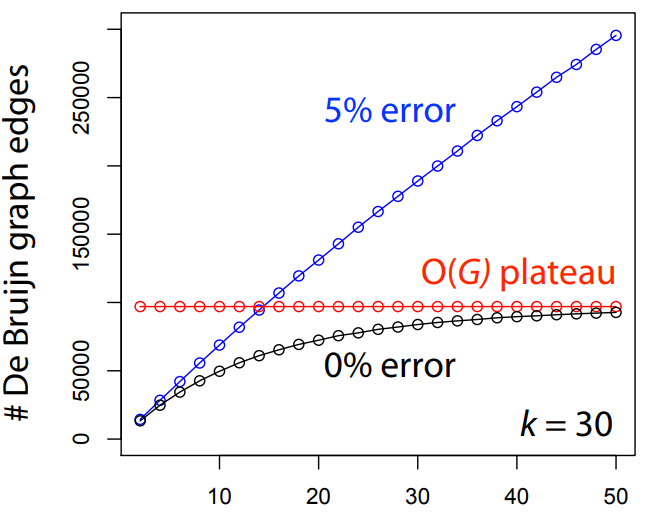
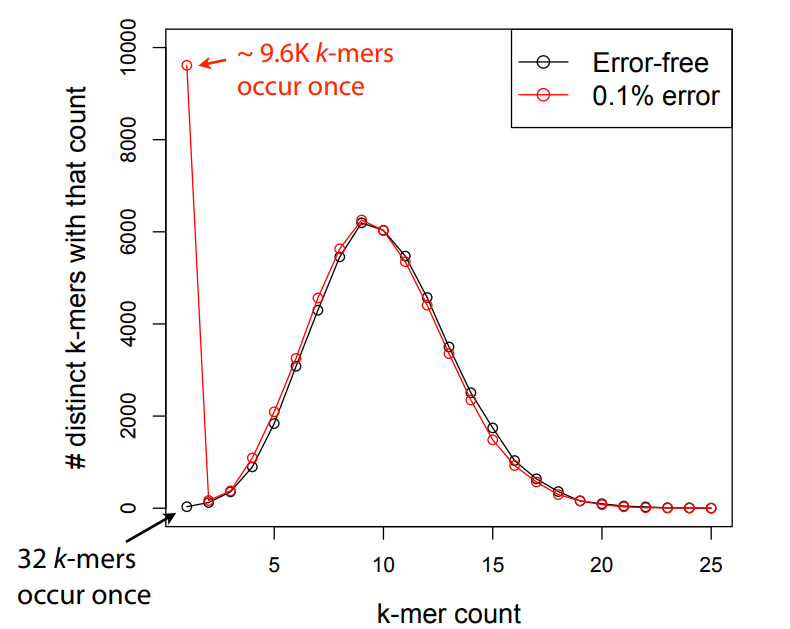
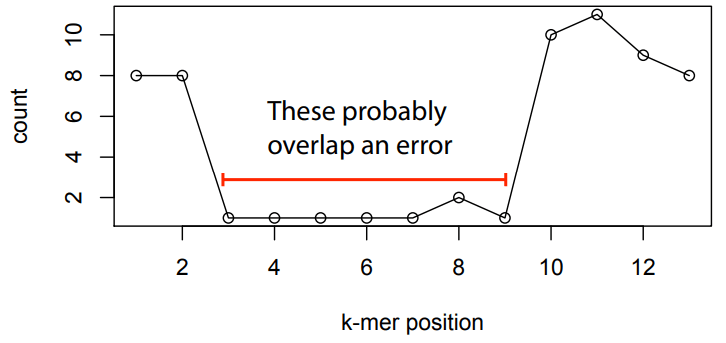
Errors affect k-mer counts
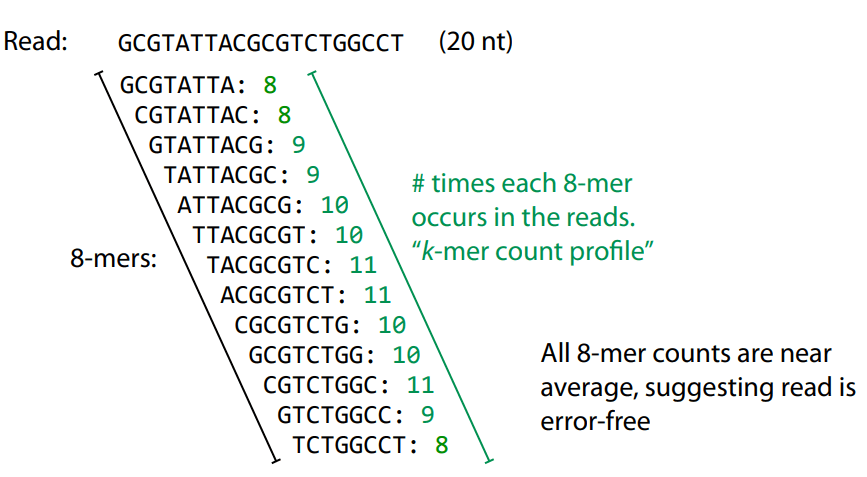

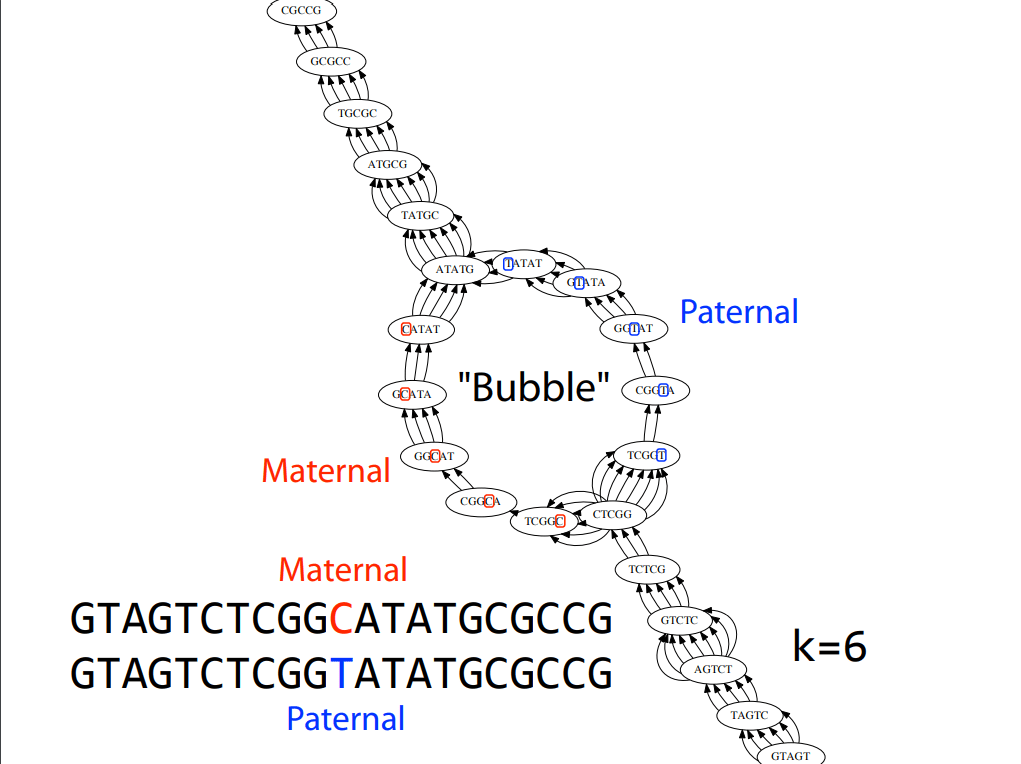
Error correction

Before the next class, you should
- Start A02, which is due next Thursday at 11:59 pm.
Lecture 05:
Gene annotation
Lecture 04:
De novo assembly
Today
Tuesday
Discord: discord.gg/zZp58KdK

(Website coming soon.)
Meetings: 9 pm on Mondays (Starting the 16th)
Location: 203 David Lawrence



