
Computational Biology

(BIOSC 1540)

Sep 19, 2024
Lecture 08:
Read mapping
Announcements
- A03 is due tonight by 11:59 pm

After today, you should be able to
1. Describe the challenges of aligning short reads to a large reference genome.
2. Compare read alignment algorithms, including hash-based and suffix tree-based approaches.
3. Explain the basic principles of the Burrows-Wheeler Transform (BWT) for sequence alignment.
We are dealing with enormous datasets
Reference genome sizes
- Homo sapiens: 3,200,000,000 bp
- Mus musculus: 2,700,000,000 bp
- Drosophila melanogaster: 140,000,000 bp
- Saccharomyces cerevisiae: 12,000,000 bp
(~3.2 GB if using u8)
RNA-seq data
Contextualization
The best movie ever is only 1.2 GB
Most computers have 8 - 12 GB of RAM

The Trade-off: Fast vs. Precise
Performance considerations
- Balancing speed and accuracy
- Efficient alignment for downstream analyses
- Resource management (CPU, memory)
After today, you should be able to
1. Describe the challenges of aligning short reads to a large reference genome.
2. Compare read alignment algorithms, including hash-based and suffix tree-based approaches.
3. Explain the basic principles of the Burrows-Wheeler Transform (BWT) for sequence alignment.
A spectrum of alignment strategies
Hash tables
Mid 2000s
Late 2000s
Late 2000s
Suffix arrays/trees
Burrows-Wheeler transforms



E.g., Bowtie2, BWA, STAR
Hash tables link a key to a value
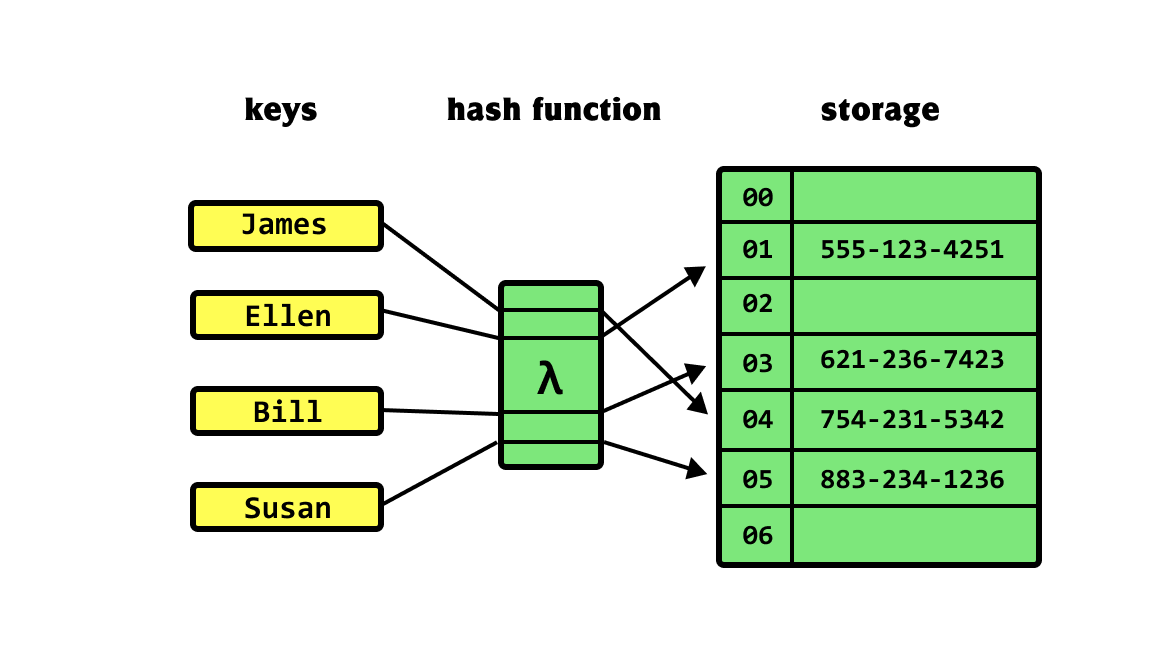
Keys represent a "label" we can use to get information
Example: Contacts
Name
A "hash function" determines where to find their number
Number
Hash functions convert labels to table indices

Index: We take the key, count how many characters are in it
Note: This is a bad hashing function since "Alex" and "John" would result in the same index
Example
len("James") = 5
James
883-234-1236
Hashing our reference genome seeds our hash table with k-mer locations
5-mers
TACGT, ACGTA, CGTAC, GTACG, . . .
Reference genome
0
10
TACGTACGATAGTCGACTAGCATGCATGCTACGTGCTAGCACGTATGCATGCATGCATGCC
20
30
40
50
60
We hash our k-mer, and add the starting index where that k-mer occurs in our reference genome
TACGT
[1, 40]
h(k)
ACGTA
[0, 29]
k-mer location in genome
k-mer
Hashing our RNA-seq data provides quick lookups of our reference genome
Query a k-mer read to get indices that of possible reference genome locations
Reference genome
0
10
TACGTACGATAGTCGACTAGCATGCATGCTACGTGCTAGCACGTATGCATGCATGCATGCC
20
30
40
50
60
Hash table
TACGT
[0, 29]
ACGTA
[1, 40]
k-mer location in genome
k-mer
h(k)
Seed-and-extend in hash-based alignment
Seed
Extend
Read: ATCGATTGCA
k-mers (k=3)
ATC, TCG, CGA, GAT, ATT, TTG, TGC, GCA
Use hash table for rapid lookup of potential matches quickly
Start from seed match and grow in both directions with reference genome
CCGTATCGATTGCAGATG
GAT
[7, 14]
h(k)
Check to see if we can align the read to reference
Hash-Based Alignment:
Divide and Conquer
A "DNA dictionary" with quick lookup and direct access to potential matches
Pros
- Easily parallelizable
- Flexible for allowing mismatches
- Conceptually simple
Cons
- Large memory footprint for index
- Can be slower for very large genomes

Suffix trees represent all suffixes of a given string
NA
NA$
$
4
2
0
1
3
5
A
$
NA
$
NA$
Root node
(Start here)
BANANA
$
A suffix tree is used to find starting index of suffix
Nowhere.
Edge
Node
Leaf node
Split point
Suffix start index
Next part of suffix
Where does start?
AANA
Index 2.
Example: Where does
start?
NANA$
Note: We use $ to represent the end of a string
Suffix arrays are memory-efficient alternatives to trees
BANANA
$
Requires less memory, but is also less powerful
1. Create all suffixes
2. Sort lexicographically
BANANA
$
ANANA
$
NANA
$
NA
$
ANA
$
A
$
$
3. Store starting indices in original string
6
5
3
1
0
4
2
Symbols come before letters for sorting
BANANA
$
ANANA
$
NANA
$
NA
$
ANA
$
A
$
$
After today, you should be able to
1. Describe the challenges of aligning short reads to a large reference genome.
2. Compare read alignment algorithms, including hash-based and suffix tree-based approaches.
3. Explain the basic principles of the Burrows-Wheeler Transform (BWT) for sequence alignment.
Compression reduces the amount of data we have to store
"Alex keeps talking and talking and talking and talking and eventually stops."
Suppose we need to store this string:
How could we store this string and save space?

"talking and talking and talking and talking and"
"talking and" 4
=
"Alex keeps talking and talking and talking and talking and eventually stops."
"Alex keeps" + "talking and" 4 +"eventually stops."
Run-length encoding
Not all strings have repeats
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Donec iaculis risus vulputate dui condimentum congue. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas.
Can you find any repeats?

How can we force repeats?
Sorting the letters does!
.aaaaaaaaaaaabbcccccccccddddddeeeeeeeeeeeeeeeeeeeeeeefggghiiiiiiiiiiiiiiiillllllllmmmmmmmmnnnnnnnnnnoooooooopppppqqrrrrrrrssssssssssssssssstttttttttttttttttttuuuuuuuuuuuuuuuv
a12b2c9d6e23f1g3h1i16l8m8n10o8p5q2r7s17t19u15v1
Run-length encoding
Sorting lexicographically forces repeats, but loses original data
The Burrows-Wheeler Transform (BWT) is a way to sort our strings without losing the original data
(And also search through it!)
Developed by Michael Burrows and David Wheeler in 1994
Basic concept of BWT
- Append a unique end-of-string (EOS) marker to the input string.
- Generate all rotations of the string.
- Sort these rotations lexicographically.
- Extract the last column of the sorted matrix as the BWT output.
BANANA
$
A
$
BANAN
NA
$
BANA
$
BANANA
ANA
$
BAN
NANA
$
BA
ANANA
$
B
BANANA
$
A
$
BANAN
NA
$
BANA
$
BANANA
ANA
$
BAN
NANA
$
BA
ANANA
$
B
ANNB$AA
BANANA
First column is more compressible, but we lose context and reversibility
(We can also get first column by sorting the output)
N
A
N
B
$
A
A
A
A
A
$
B
N
N
A
A
A
$
B
N
N
N
A
N
B
$
A
A
AN
AN
A$
$B
BA
NA
NA
AN
AN
A$
$B
BA
NA
NA
N
A
N
B
$
A
A
ANA
ANA
A$B
$BA
BAN
NAN
NA$
ANA
ANA
A$B
$BA
BAN
NAN
NA$
N
A
N
B
$
A
A
BWT output is reversible!
ANAN
ANA$
A$BA
$BAN
BANA
NANA
NA$B
BANANA$
NANA$BA
NA$BANA
A$BANAN
$BANANA
ANANA$B
ANA$BAN
- Write BWT output "vertically"
- Sort each row starting from the left-most character
- Append the same BWT output
- Repeat until finished (length of rows equal BWT output length)
2
3
2
3
2
3
2
...
Enhancing BWT for Rapid Searching
ABRACADABRA$
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
$
A
A
A
A
A
B
B
C
D
R
R
A
R
D
$
R
C
A
A
A
A
B
B
The backward search algorithm efficiently finds occurrences of a pattern in a text using the LF-mapping
BWT matrix
Number
Number characters with the number of times they have appeard
F-column
L-column
ABRACADABRA$
ABRA
Suppose I want to find where
is located
1. Find rows with last character in search string (e.g., A) in F-column
2. Note which rows has the next letter (e.g., R) in L-column
3. Work backwards in search string until the first letter
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
A
R
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
R
B
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
B
A
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
Backward search enables efficient searching using only first and last columns of BWT
BWT practice
Given the string "mississippi$", complete the following tasks:
- Construct the Burrows-Wheeler Transform (BWT) of the string.
- Use the LF-mapping to find the number and positions of occurrences of the following patterns in the original string:
- a) "si"
- b) "iss"
- c) "pp"
Before the next class, you should
- Submit A03
- Start A04
Lecture 09:
Quantification
Lecture 08:
Read mapping
Today
Tuesday