

Computational Biology
(BIOSC 1540)
Oct 17, 2024
Lecture 13:
Molecular simulation principles
Announcements
- A05 is due Oct 24 at 11:59 pm

After today, you should be able to
Understand the importance of molecular dynamics (MD) simulations for proteins.
Proteins undergo movements like folding, unfolding, and domain motions
These motions are essential for binding, catalysis, and signal transduction
Understanding dynamics is crucial for drug design, protein design, biotech, etc.

Protein structure determination and prediction provide fixed snapshots
Do not capture the full range of functional conformations
Molecular dynamics (MD) provide time-resolved insights into protein behavior
Simulation of Atomic Movements
- MD computes trajectories of atoms over time scales of femtoseconds to microseconds.
- It can capture both small-scale vibrations and large-scale conformational changes.
Visualization and Analysis:
- Provides detailed information on atomic interactions and energy changes.
- Enables the study of mechanisms at an atomic level.
MD simulations provide more realistic analysis of proteins
Refinement of Predicted Structures:
- MD helps minimize energy and relax structures obtained from modeling.
- Improves accuracy by accounting for environmental effects.
Studying Intrinsically Disordered Proteins:
- MD captures the flexible nature of disordered regions.
- Aids in understanding functions that depend on disorder.
Folding and Misfolding Pathways:
- Simulates the folding process to identify intermediates.
- Investigates misfolding mechanisms relevant to diseases.
After today, you should be able to
Identify the validity of the classical approximation
In biomolecular MD simulations, atoms are treated as classical particles
We treat atoms as hard spheres

Quantum mechanics
Classical mechanics
Classical approximations neglect quantum effects
Classical Mechanics
- Describes the motion of macroscopic objects.
- Assumes particles have well-defined positions and velocities.
- Governed by Newton's Laws of Motion.
Quantum Mechanics
- Necessary for describing behavior at atomic and subatomic scales.
- Accounts for wave-particle duality, uncertainty principle, proton tunneling
- Electrons exhibit quantum behavior that cannot be captured classically.
Classical approximation impacts
- Nuclei (protons and neutrons) are much heavier than electrons.
- Their de Broglie wavelengths are very small, making quantum effects less significant.
- At room temperature and above, thermal energies dominate over quantum zero-point energies.
Nuclei
- Electrons are not explicitly simulated in classical MD.
- Their effects are included implicitly through potential energy functions (force fields).
- The electronic structure is assumed to remain in the ground state during simulation.
Electrons
Classical approximations are valid in most biomolecular cases
Suitable Systems:
- Biological macromolecules (proteins, nucleic acids, lipids).
- Materials where electronic excitations are not critical.
- Processes where bond breaking/forming does not occur.
Limitations:
- It cannot accurately simulate chemical reactions involving electronic transitions.
- Quantum phenomena like tunneling and zero-point energy are not captured.
After today, you should be able to
Discuss the concept of equations of motion in MD simulations.
Classical particles follow Newton's equations of motion
Newton's Second Law
The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass
Given atomic forces, we can calculate atomic movements
Force vector acting on the particle [kcal/mol/Å]
Mass of the particle [amu]
Acceleration vector of the particle [Å/fs2]
How can we compute atomic forces?
Forces are the negative gradients of potential energy
The potential energy, U, is dependent on positions of all atoms
Forces are obtained from the negative gradient of potential energy
Determines acceleration and thus motion of atoms
Time evolution of the system is computed by integrating equations of motion
Continuous motion approximated using discrete time steps
- Determine forces
- Move a small amount forward in time
- Repeat

Time step length determines how "smooth" the animation/trajectory
Think claymation
Molecular simulations compute an atomistic trajectory



3D coordinates of atoms in our system
These atoms exert forces on each other
Using Newton's equation of motion, we can predict their movement
After today, you should be able to
Explain the role of integration algorithms in MD simulations.
Integration Algorithms Numerically Solve the Equations of Motion in Molecular Dynamics
Purpose of Integration Algorithms:
- Numerical Solution: Approximate the continuous equations of motion using discrete time steps.
- Update Positions and Velocities: Calculate the new positions and velocities of particles based on current forces.
Challenges Addressed by Integration Algorithms:
- Stability: Prevent numerical errors from accumulating over many time steps.
- Accuracy: Ensure that the trajectories closely follow the true physical behavior.
- Efficiency: Balance computational speed with the precision of the simulation.
Common Integration Algorithms
Verlet: Uses current and previous positions to calculate the next position
Velocity Verlet: An extension of the Verlet algorithm that explicitly calculates velocities
Time step length determines how "smooth" the trajectory
Say we want to simulation system for 100 fs
Smaller time steps lead to more calcualtions to simulate same amount of time
0.5 fs
200
Number of total atomic force calculations
1.0 fs
100
2.0 fs
50
After today, you should be able to
Describe the components of a molecular mechanics force field.
We use "force fields" to compute energies and atomic forces

How can we do this quickly and accurately for large systems (e.g., proteins)?
How can we decompose dynamics into fundamental atomic motions?
GFN2-xTB; 1 fs time step; 1000 fs
Let's consider a QM simulation a single methanol molecule (H3COH)
How would we model these atomistic dyanmics classically?
The dynamics of a molecule can be described as combinations of ...
Bond lengths
Bond angles
Dihedral angles
Chemical bonds behave like springs
Two spheres (atoms) connected by a single spring
The spring resists changes in the distance between the two atoms
Approximate bond vibrations as harmonic oscillators
We can also get the force
Equilibrium bond length
Current bond length
Spring constant (i.e., bond stiffness)
Spring constants are determined by bond order

CISD/cc-pVTZ



Single
Double
Triple
(These are approximate values.)

Spring constants are determined by bond order and atom types
We can model each type of bond with a specific spring constant
Bond angles behave like ...
harmonic oscillators
We also have separate spring constants for bond angles
Three balls connected by two springs forming an angle, with a "hinge" at the central atom.
A dihedral angle is the angle between two planes
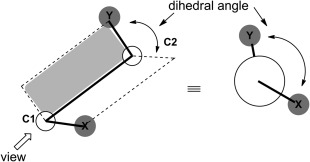
A dihedral angle is the angle between two planes formed by four sequentially bonded atoms (A–B–C–D)
It describes the rotation around the bond between atoms B and C
The dihedral angle 𝜙 is the angle between these two planes
Dihedral angles behave ... not like springs

Energies are computed with MP2/cc-pVTZ
Dihedrals vs. Bonds and Angles
- Bonds and Angles: Govern local geometry (bond lengths and bond angles) using quadratic (harmonic) potentials that favor specific distances and angles.
- Dihedrals: Govern torsional or rotational flexibility around bonds, typically using periodic or multi-well potentials to allow for multiple stable conformations.
Dihedral potentials must capture arbitrary functions with rotational symmetry
Here, we have a periodic energy function with varying minima
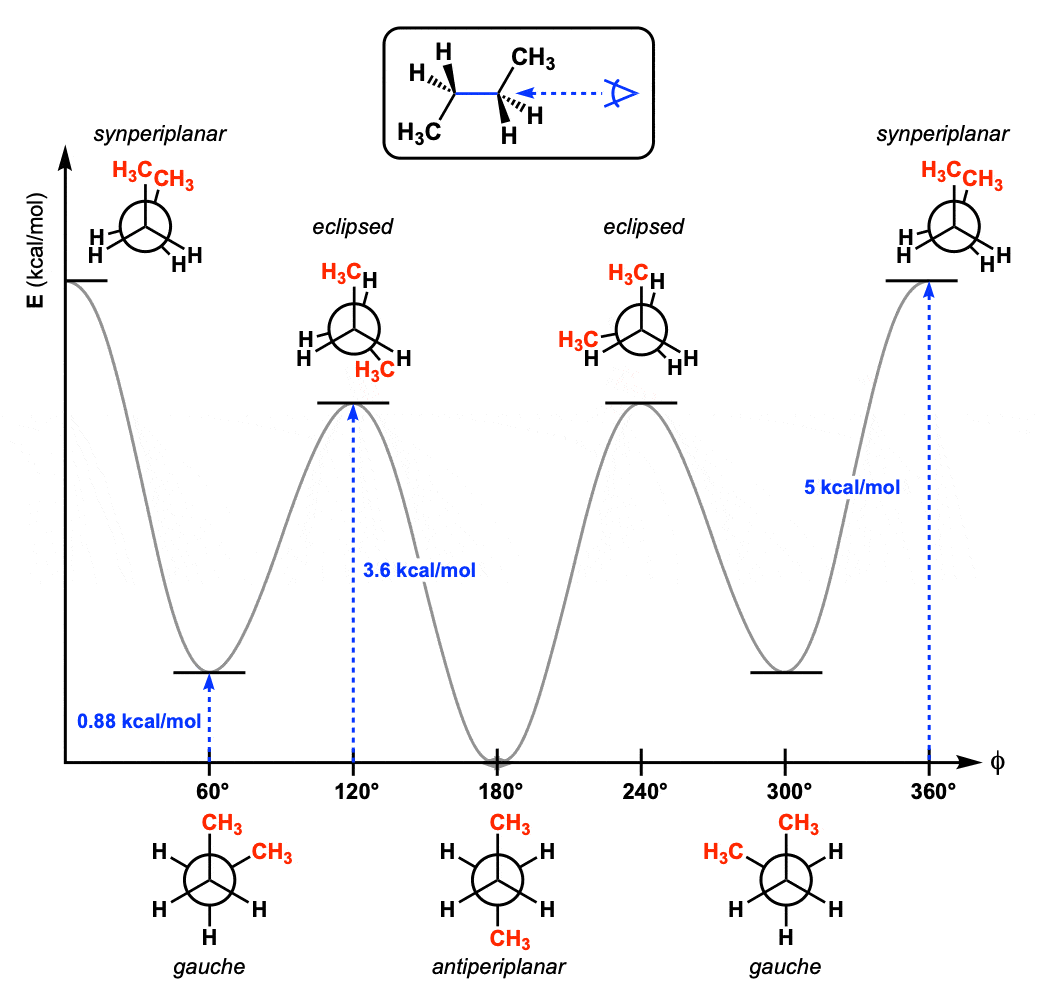
How do we model this?
Fourier Series approximate functions as a sum of sine and cosine waves
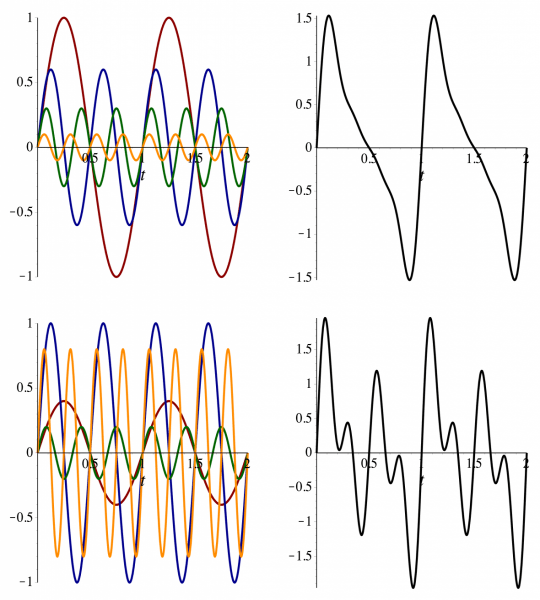



Fourier series can approximate (any) symmetrical rotational energy function


Constant term (i.e., average of function)
Amplitude coefficients
Harmonic number (i.e., frequency)
Higher harmonics add finer details to the approximation, enhancing the accuracy of the representation
Adding more sine and cosine terms improves the approximation, allowing the Fourier Series to closely match the original complex function
Dihedral potentials use custom Fourier series
Dihedral angle
Amplitude for n-th Fourier
Phase shift
Number of periodic terms
Sum of all bonded terms provides a single-molecule force field

We rarely simulate one molecule; what about multiple?
After today, you should be able to
Understand noncovalent contributions to force fields.
Noncovalent Interactions Are Crucial for Simulating Multiple Molecules in MD
Role in Molecular Assembly:
-
Facilitate the organization of molecules into complex structures.
- Determine the macroscopic properties of materials (e.g., solubility, melting points).
Importance in Biological Systems:
- Govern essential processes like enzyme-substrate binding, protein folding, and membrane formation.
- Critical for understanding biochemical pathways and drug design.
While covalent bonds define the primary structure of molecules, noncovalent interactions are pivotal in dictating how molecules interact
Dispersion Forces
- Nature: Weak, attractive forces arising from instantaneous dipoles in molecules.
- Role: Stabilize molecular assemblies by promoting close packing.
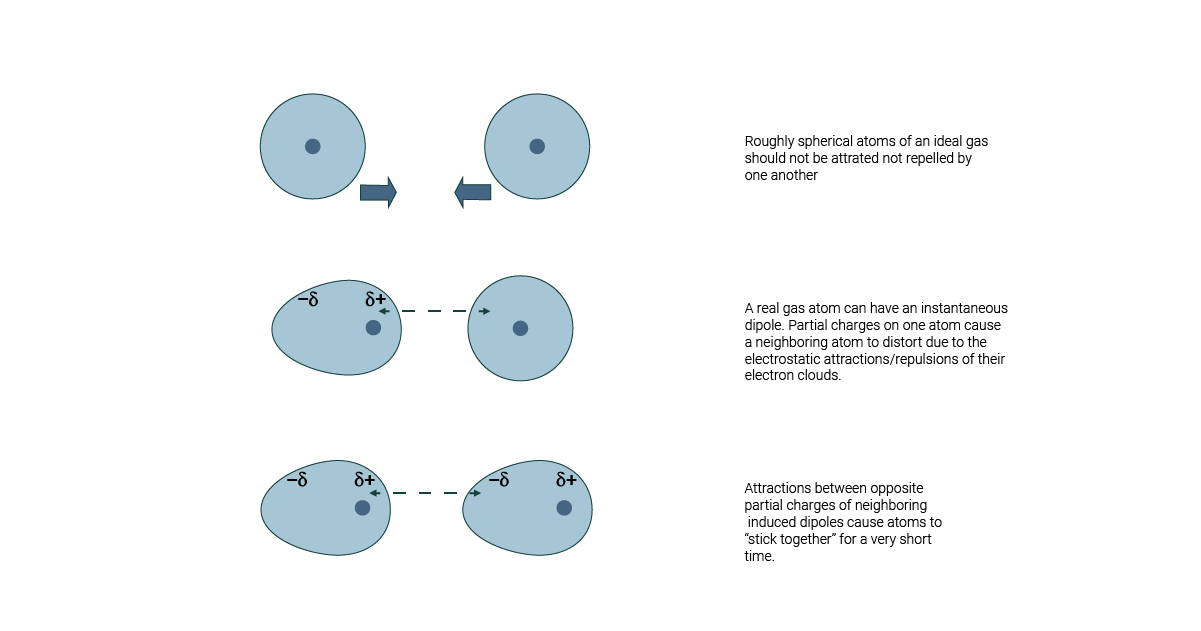
Dispersion coefficient
Repulsion Forces
- Nature: Strong, short-range forces due to overlapping electron clouds.
- Role: Prevent atoms from collapsing into each other, maintaining molecular integrity
Repulsion coefficient
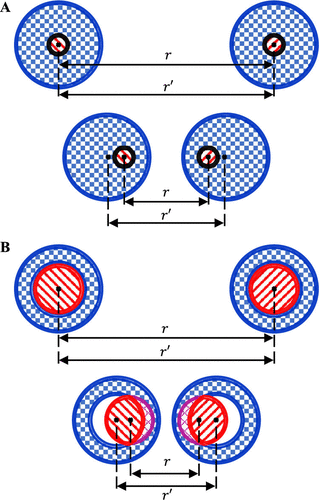
Combined van der Waals Potential
Van der Waals forces are modeled using the Lennard-Jones potential, which captures both the attractive and repulsive aspects of noncovalent interactions
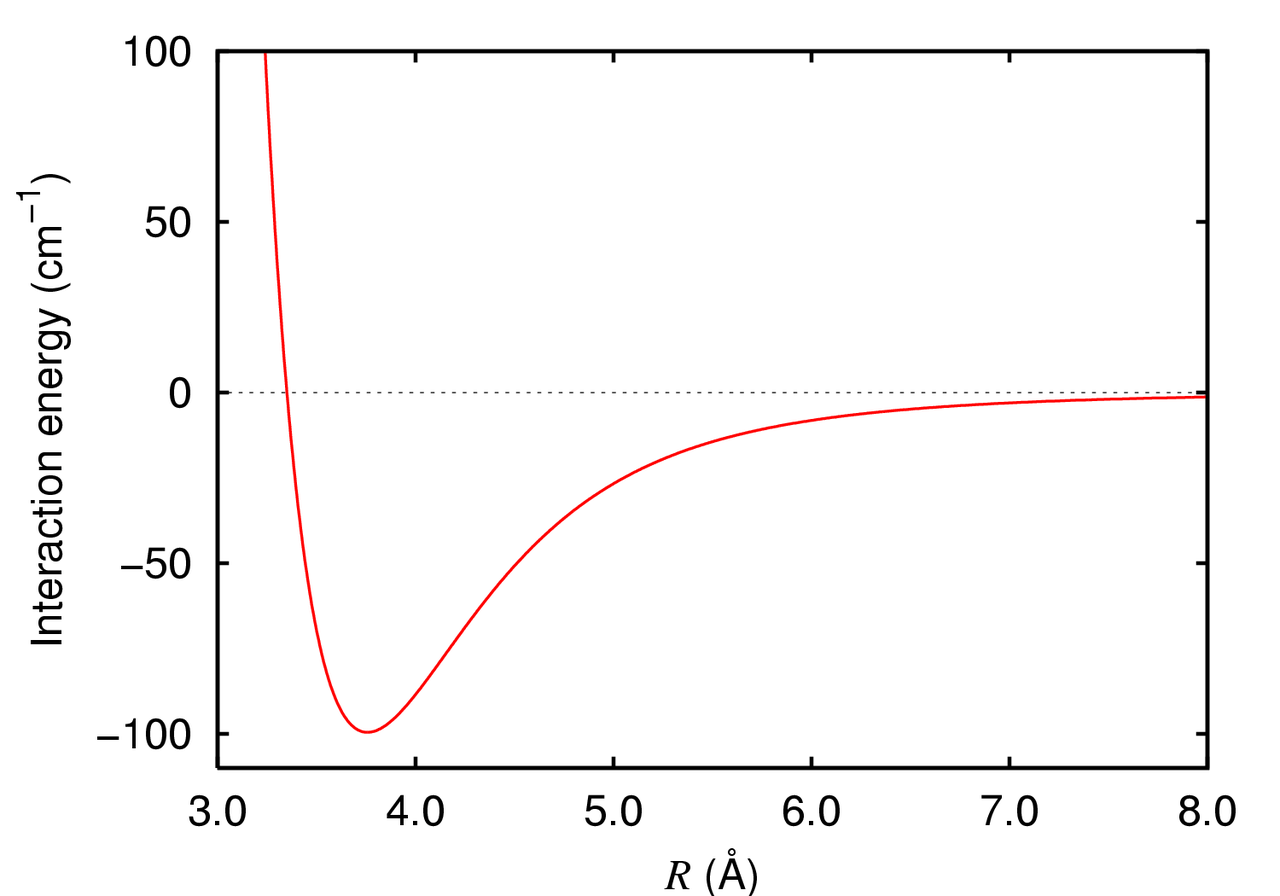
Electrostatic Interactions Drive Charged and Polar Molecule Behavior
Electrostatic forces decay as 1/r, making them significant over longer distances compared to van der Waals forces
Bonded and nonbonded interactions make our complete force field

After today, you should be able to
Identify data for force field parameterization
Parameterizing Force Fields Begins with Quantum Mechanical Data for Small Molecules
Role of Quantum Mechanics:
- QM Calculations: Provide high-accuracy data on molecular geometries, energetics, and electronic distributions.
- Data Utilization: QM data inform the selection and tuning of force field parameters to ensure they reflect true molecular behavior.
Small Molecule Focus:
- Simplicity: Smaller molecules have fewer atoms and simpler interactions, making QM calculations more manageable.
- Accuracy: QM methods (e.g., Density Functional Theory, Hartree-Fock) yield precise information essential for initial parameterization.
From Small Molecules to Proteins: Increasing Complexity in Force Field Parameterization
Complexity of Proteins:
- Size and Structure: Proteins consist of hundreds to thousands of atoms with intricate three-dimensional structures.
- Diverse Interactions: Include a variety of noncovalent interactions, such as hydrogen bonds, ionic bonds, hydrophobic interactions, and van der Waals forces.
Limitations of QM for Large Systems:
- Computational Cost: QM calculations become computationally prohibitive for large biomolecules like proteins.
- Alternative Strategies: Utilize QM data from representative small segments or use empirical and semi-empirical methods.
Experimental Data Are Crucial for Refining Force Field Parameters
Types of Experimental Data:
- Spectroscopic Data: Infrared (IR), Nuclear Magnetic Resonance (NMR), and Raman spectroscopy provide insights into bond vibrations and molecular geometries.
- Crystallography: X-ray crystallography offers precise information on atomic positions and molecular conformations.
- Thermodynamic Measurements: Data on melting points, boiling points, and solvation energies inform interaction strengths.
Parameter Optimization:
- Fitting Process: Adjust force field parameters to minimize discrepancies between simulation results and experimental observations.
- Validation Metrics: Use root-mean-square deviation (RMSD), binding affinities, and structural stability as benchmarks.
Fitting Force Field Parameters to Experimental Data Ensures Realistic Simulations
Parameter Adjustment:
- Process: Fine-tune force field parameters to minimize discrepancies between simulation outcomes and experimental observations.
- Techniques: Use of optimization algorithms and statistical methods to achieve best-fit parameters.
Iterative Refinement:
- Feedback Loop: Use simulation results to identify parameter inaccuracies and iteratively adjust them based on experimental data.
- Continuous Improvement: Enhance force field accuracy through ongoing comparisons and adjustments.
Challenges in Parameterizing Force Fields for Proteins
High Dimensionality:
- Issue: Proteins possess numerous degrees of freedom, making comprehensive parameterization computationally intensive.
- Solution: Utilize advanced optimization techniques and high-performance computing resources.
Diverse Chemical Environments:
- Issue: Different regions of a protein (e.g., active sites, hydrophobic cores) experience varied chemical environments.
- Solution: Develop region-specific parameters or use adaptive force fields that can account for environmental variations.
Challenges in Parameterizing Force Fields for Proteins
Dynamic Conformational Changes:
- Issue: Proteins frequently undergo conformational shifts that must be accurately captured by the force field.
- Solution: Incorporate flexible dihedral terms and ensure that parameters support a wide range of conformational states.
Long-Range Electrostatic Interactions:
- Issue: Accurate modeling of electrostatics in large, charged systems is computationally demanding.
- Solution: Implement efficient algorithms like Particle Mesh Ewald (PME) and use approximations where appropriate.
Summary of Force Field Parameterization Process
Step-by-Step Process:
- Quantum Mechanical Calculations: Obtain high-accuracy data for small molecules and representative fragments.
- Empirical Data Integration: Incorporate experimental measurements to validate and refine parameters.
- Parameter Optimization: Adjust force field parameters through iterative simulations and comparisons.
- Advanced Techniques: Utilize machine learning, multi-scale modeling, and automated pipelines to enhance parameter accuracy and efficiency.
Different force fields are tailored for specific types of molecules and applications
-
Common Force Fields:
- AMBER: Optimized for proteins and nucleic acids.
- CHARMM: Versatile, used for a wide range of biomolecules.
- OPLS: Focuses on liquids and organic molecules.
-
Selection Criteria:
- Compatibility with the system being studied.
- Availability of parameters for the molecules of interest.
-
Limitations:
- Force fields are approximations and may not capture all interactions.
- Ongoing development aims to improve accuracy and transferability.
Before the next class, you should
- Work on A05
- Review material
Lecture 13:
Molecular simulation princples
Today
Tuesday
Lecture 14:
Molecular system representations