Local Composition Models

CHE 2101 - Spring 2022

April 21, 2022

Reference material: Rowley chapters 5 and 9

Lecture 25

van der Waals Mixture Partition Function

Learning Objective

Partition functions are normalization constants

Expectation values of some property

\left\langle J \right\rangle = \sum\limits_k \frac{J_k e^{-\beta U_k}}{Q}
J

Semi-classical partition function

Q = \frac{Z q_{int}^N}{N! \Lambda^{3N}}

What is the meaning of each term?

\frac{q_{int}}{\Lambda^{3}}

Molecular partition function

Q

System partition function

N!

Indistinguishability of molecules

Z

Configurational partition function

Partition functions review

Configurational partition function

That makes sense, right?

Z = \int \cdots \int e^{-\beta U} dq^{3N}

Not to me

Partition functions review

Configurational partition function - Toy system

Angle-averaged interaction energy of water dimer (HW 7)

e^{-\beta U}
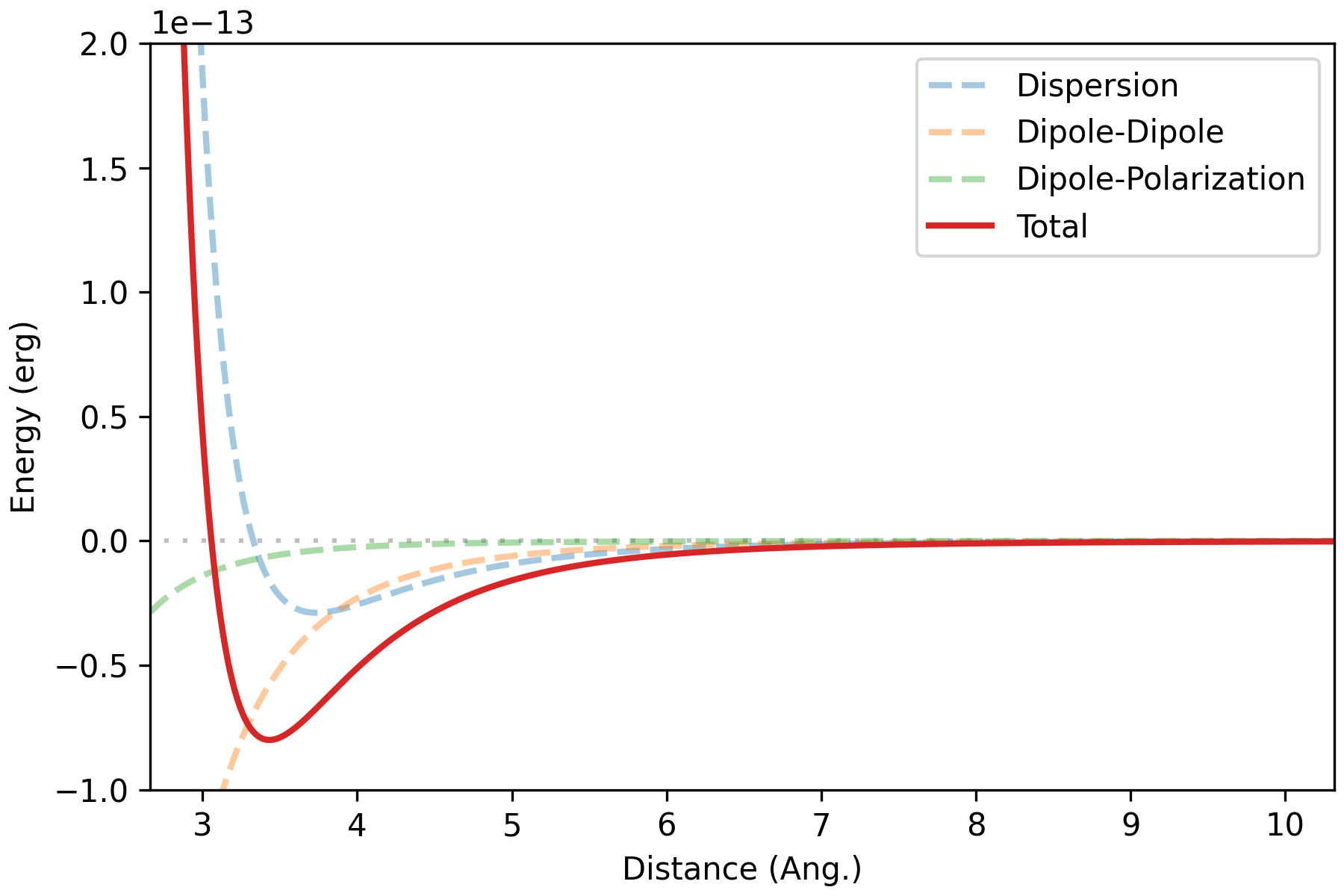
T = 298.15  # K
beta = 1/(kB * T)  # 1/erg
bolz_factor = np.exp(-beta*u_total)
Z = np.sum(bolz_factor)  # 116691.201
prob = bolz_factor/Z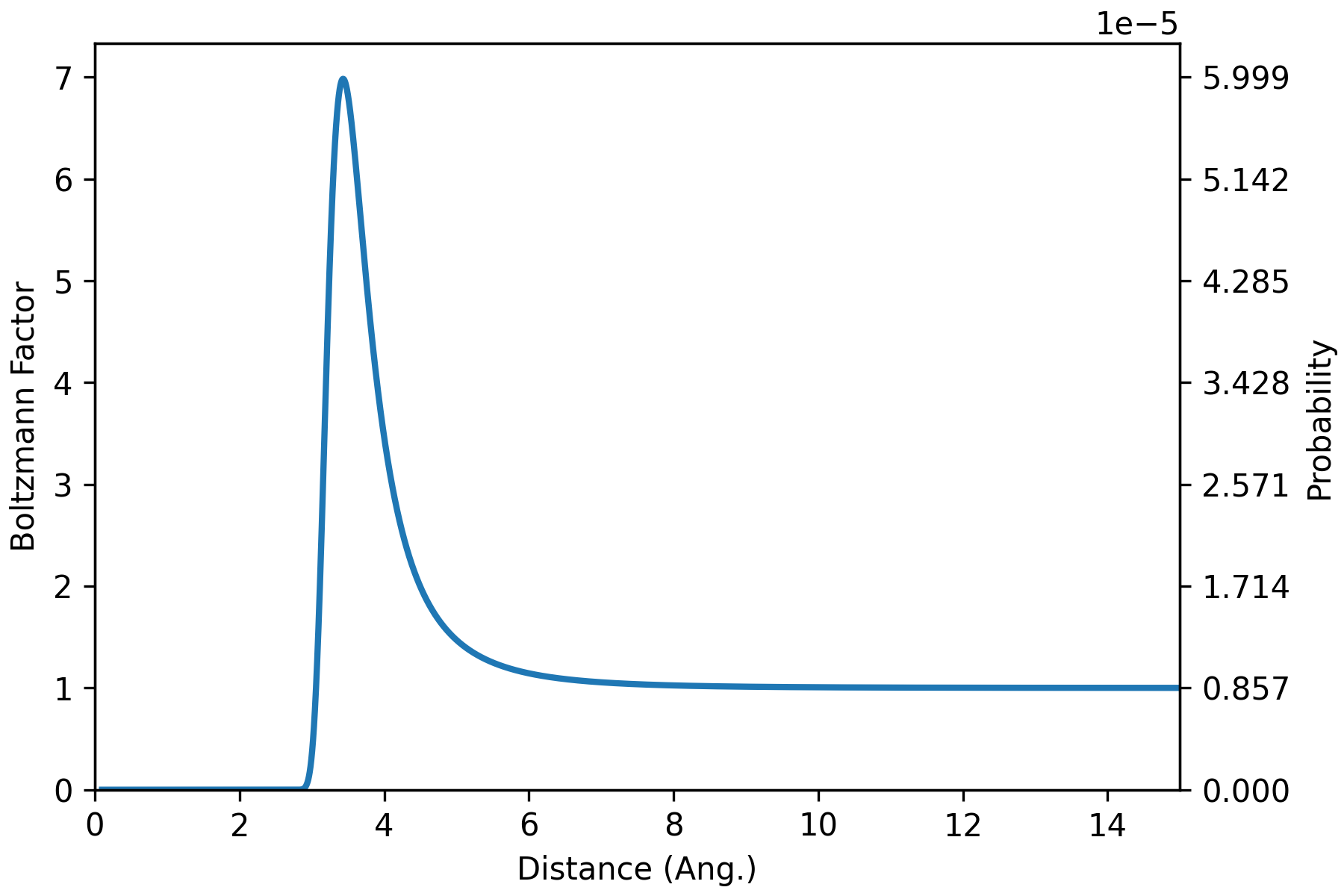
Z = \int \cdots \int e^{-\beta U} dq^{3N}
dq^{3N} = dr

Partition functions review

Partition functions review

Z for real systems would have 3N dimensions

Approximations are needed for analytical expressions

Configurational partition function - Real systems

For example: van der Waals partition function

Approximations/Approach

  • Liquid molecules constrained in "lattice" cages
  • Total potential energy is pairwise additive
  • Mean-field pairwise potential
  • No correlation between cages

Review from lecture 20

Partition functions review

Conceptualizing vdW framework

Lattice cage confining some molecule

Molecules do not respond to the motion of neighbors
(i.e., no correlation)

Review from lecture 20

Partition functions review

vdW partition function

Z_{vdW} = V_f^N \exp \left( - \frac{N u_0}{2 k_B T} \right)
V_f = \left[ \frac{4 \pi (a_1 - d)^3}{3} \right]
  • Free volume: Cage volume accessible to the center of the hard sphere
    • Two parameters
  • The exponential term is the lattice potential contribution
    • The potential energy of a molecule exploring its cage
Q_{vdW} = \frac{Z_{vdW} q_{int}^N}{N! \Lambda^{3N}}
a_1
d

Lattice information

Molecular diameter

u_0

Averaged lattice potential

Review from lecture 20

Takeaways

  • Analytical expressions for Z are challenging
  • vdW partition functions provide a framework for approximating Z

I learned

this

You learned

this?

I learned

this

Alex

You

Helmholtz Free energy of Mixing

Learning Objective

Disclaimer: Assuming

\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)

Helmholtz free energy of mixing

Q_{vdW} = \frac{\left( q_{1, int} \right)^{N_1} \left( q_{2, int} \right)^{N_2}}{N_1! N_2! \Lambda_1^{3N_1} \Lambda_2^{3N_2}} V_f^N \exp \left( - \frac{N \beta u_0}{2} \right)
\Delta A_{mix} = A_{m} - A_1^0 - A_2^0\\ = -k_B T \ln \left( \frac{Q_m}{Q_1^0 Q_2^0} \right)
A = - k_B T \ln Q
  • vDW partition function for mixtures
  •       ,     ,       all cancel leaving you with
q_{int}
N
\Lambda^{3N}
\Delta A_{mix} = -k_B T \ln \left( \frac{V_{f}^{N}}{V_{f, 1}^{N_1} V_{f, 2}^{N_2}} \right) + \frac{1}{2} \left( N u_0 - N_1 u_{0, 1} - N_2 u_{0, 2} \right)
\Delta A_{mix} =
\Delta A_{athermal}
\Delta A_{resid}
+

Entropic effects based on free volume differences

Energetic differences between like and unlike interactions

Calculating

\Delta A_{mix}
  • Put final minus initial Helmholtz free energy in terms of partition functions

Helmholtz free energy of mixing

Possible assumption 1/2

Athermal contribution

Free volume is proportional to N

\Delta A_{atherm} = -k_B T \ln \left( \frac{V_{f}^{N}}{V_{f, 1}^{N_1} V_{f, 2}^{N_2}} \right)
\Delta A_{atherm} = - k_B T \ln \left( \frac{N^{N}}{N_1^{N_1} N_2^{N_2}} \right)
\Delta A_{atherm} = - k_B T \ln \left( \frac{N^{N_1 + N_2}}{(x_1 N)^{N_1} (x_2 N)^{N_2}} \right)
= k_B T \ln \left( x_1^{N x_1} x_2^{N x_2} \right)
= N k_B T \ln \left( x_1^{x_1} x_2^{x_2} \right)

Use

N_i = x_i N

Ideal mixture model

\Delta A_{atherm}^{id}
\Delta A_{atherm} = \Delta A_{atherm}^{id} + A_{atherm}^{E}

Would this be always positive, negative, or does it depend? Why?

Helmholtz free energy of mixing

Possible assumption 2/2

Athermal contribution

\Delta A_{atherm} = -k_B T \ln \left( \frac{V_{f}^{N}}{V_{f, 1}^{N_1} V_{f, 2}^{N_2}} \right)
\Delta A_{atherm} = -k_B T \ln \left( \frac{V_{m}^{N}}{V_{1}^{N_1} V_{2}^{N_2}} \right)

Define volume fraction as

= k_B T \ln \left( \frac{V_1^{N_1} V_2^{N_2}}{V_m^{N_1} V_m^{N_2}} \right)
\phi_i = V_i / V_m
= k_B T \ln \left( \phi_1^{N_1} \phi_2^{N_2} \right)
= k_B T \left[ N_1 \ln \left( \phi_1 \right) + N_2 \ln \left( \phi_2 \right) \right]

Flory-Huggins Equation

Free volume if proportional to molar volume

V_{f, i} \propto V_i

Helmholtz free energy of mixing

Residual contribution

Direct expressions are rare, so we use this instead

\Delta A_{resid} =\frac{1}{2} \left( N u_0 - N_1 u_{0, 1} - N_2 u_{0, 2} \right)
\Delta A_{resid} = T \int\limits_0^{1/T} \Delta U_{resid} \; d \left( \frac{1}{T} \right)

Easy, right?

Local composition models can accomplish this

Now we just need to find

\Delta U_{resid}

Ehh

Takeaways

  • Use vdW partition function for Helmholtz free energy of mixing
  • Ways to compute the athermal contribution
  • Can use local composition models for residual contribution

I learned

this

You learned

this?

I learned

this

Alex

You

Local composition models

Learning Objective

Disclaimer: Assuming

\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)

Review: Pair correlation function

Configurational integrals for real systems are challenging

Relative probability of finding a second molecule some distance away

Pair correlation function (   ) is a proxy for configurational information

g

1

Distance

g

Coordnation shells

Review from lecture 20

Review: Pair correlation functions

Number of neighboring molecules

d N_r = \rho g (r) \; d \bold{r}

Differential number of atoms in a shell r distance away

is the numerical density of the system

\rho

is a volume element

d \bf{r}
d \bold{r} = \int\limits_0^{2 \pi} \int\limits_0^\pi r^2 \sin \theta \; d \theta \; d \phi \; dr = 4 \pi r^2 \; dr
= 4 \pi r^2 \rho g (r) \; dr

Total number of atoms within a distance r

N (r) = 4 \pi \rho \int\limits_0^r r^2 g (r) \; dr

What happens if we integrate to     ?

\infty

Review from lecture 20

Local composition models

Computing local compositions

N_{21} = 4 \pi \rho_2 \int\limits_0^L g_{21} (r) r^2 \; dr
N_{12} = 4 \pi \rho_2 \int\limits_0^L g_{12} (r) r^2 \; dr
x_{21} = \frac{N_{21}}{\sum\limits_k N_{k1}} = \frac{4}{6}

Type 1

Type 2

Number of type 2 moleucles around type 1

Number of type 1 moleucles around type 2

x_{12} = \frac{N_{12}}{\sum\limits_k N_{k2}} = \frac{4}{6}

Local composition models

Computing local compositions

x_{11} = \frac{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr}{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr \; + \; 4 \pi \rho_2 \int\limits_0^L g_{21} (r) r^2 \: dr}

We can use radial distribution functions to compute local mole fractions

For example, the mole fraction of type 1 molecules around another type 1

Local composition models

Computing local compositions

G_{21} = \frac{4\pi \int\limits_0^L g_{21} (r) r^2 \; dr}{4\pi \int\limits_0^L g_{11} (r) r^2 \; dr}

We can simplify this expression by considering differences in random mixing

Probability ratio of finding type 2 molecules over type 1

Example: 50:50 mixture

N_2 = N_1
N_2 > N_1
N_2 < N_1
G_{21} = 1
G_{21} > 1
G_{21} < 1

Number of neighboring molecules

Mixing factor

x_{11} = \frac{x_1}{x_1 + x_2 G_{21}}
x_{21} = \frac{x_2 G_{21}}{x_1 + x_2 G_{21}}
x_{11} = \frac{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr}{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr \; + \; 4 \pi \rho_2 \int\limits_0^L g_{21} (r) r^2 \: dr}

Local composition models

Circling back to

We can now estimate                using this concept of nonrandom mixing factors 

\Delta A_{resid}
\Delta A_{resid}

Wilson Model

Assumptions

  • Potentials of mean force are used instead of pair potentials
  • Shell thickness is the first coordination shell
\Delta U_{resid} = x_1 x_2 \left[ \frac{\left( \left\langle u \right\rangle_{21} - \left\langle u \right\rangle_{11} \right) G_{21}}{x_1 + x_2 G_{21}} + \frac{\left( \left\langle u \right\rangle_{12} - \left\langle u \right\rangle_{22} \right) G_{12}}{x_2 + x_1 G_{12}} \right]
A_{resid}^E = - RT \left[ x_1 \ln \left( x_1 + x_2 G_{21} \right) + x_2 \ln \left( x_2 + x_1 G_{12} \right)\right]
G_{ji} = \frac{V_{j}}{V_{i}} \exp \left[ - \frac{\lambda_{ij}}{RT} \right]
\lambda_{21} = \left\langle u \right\rangle_{21} - \left\langle u \right\rangle_{11}

Disclaimer: Assuming

\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)

Local composition models

Circling back to

\Delta A_{resid}

Nonrandom two-liquid (NRTL) model

Introduces nonrandom mixture parameters

G_{ij} = \exp \left( - \frac{\alpha a_{ij}}{RT} \right)
\alpha
a_{ij}
A_{resid}^E = RT x_1 x_2 \left( \frac{\tau_{21} G_{21}}{x_1 + x_2 G_{21}} + \frac{\tau_{12} G_{12}}{x_2 + x_1 G_{12}} \right)

Disclaimer: Assuming

\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)

Local composition models

Activity coefficients

Both local models can compute acitivty coefficients 

ln \left( \lambda_{1} \right) = - \ln \left( x_1 + x_2 G_{21} \right) - x_2 \left( \frac{G_{12}}{x_2 + x_1 G_{12}} - \frac{G_{21}}{x_1 + x_2 G_{21}} \right)

Wilson

NRTL

ln \left( \lambda_{1} \right) = x_2^2 \left[ \tau_{21} \left( \frac{G_{21}}{x_1 + x_2 G_{21}} \right)^2 + \frac{\tau_{12} G_{12}}{\left( x_2 + x_1 G_{12} \right)^2} \right]

Takeaways (final)

  • Pair correlation functions are a proxy for configurational information
  • Deviations in spatial compositions provide information on nonideal mixing
  • Local models can be used to compute activity coefficients and energy of mixing

I learned

this

You learned

this?

I learned

this

Alex

You