Towards Atomistic Modeling of Complex Environments with Many-Body Machine Learning Potentials

Alex M. Maldonado

September 1, 2022

aalexmmaldonado

Keith Group

Clean energy is growing, but slowly

Advancing energy technologies

Nuclear power

Molten salts

Nuclear Reactor by Olena Panasovska from Noun Project

Batteries

Electrolyte by M. Oki Orlando from Noun Project

Charge carriers and electrolytes

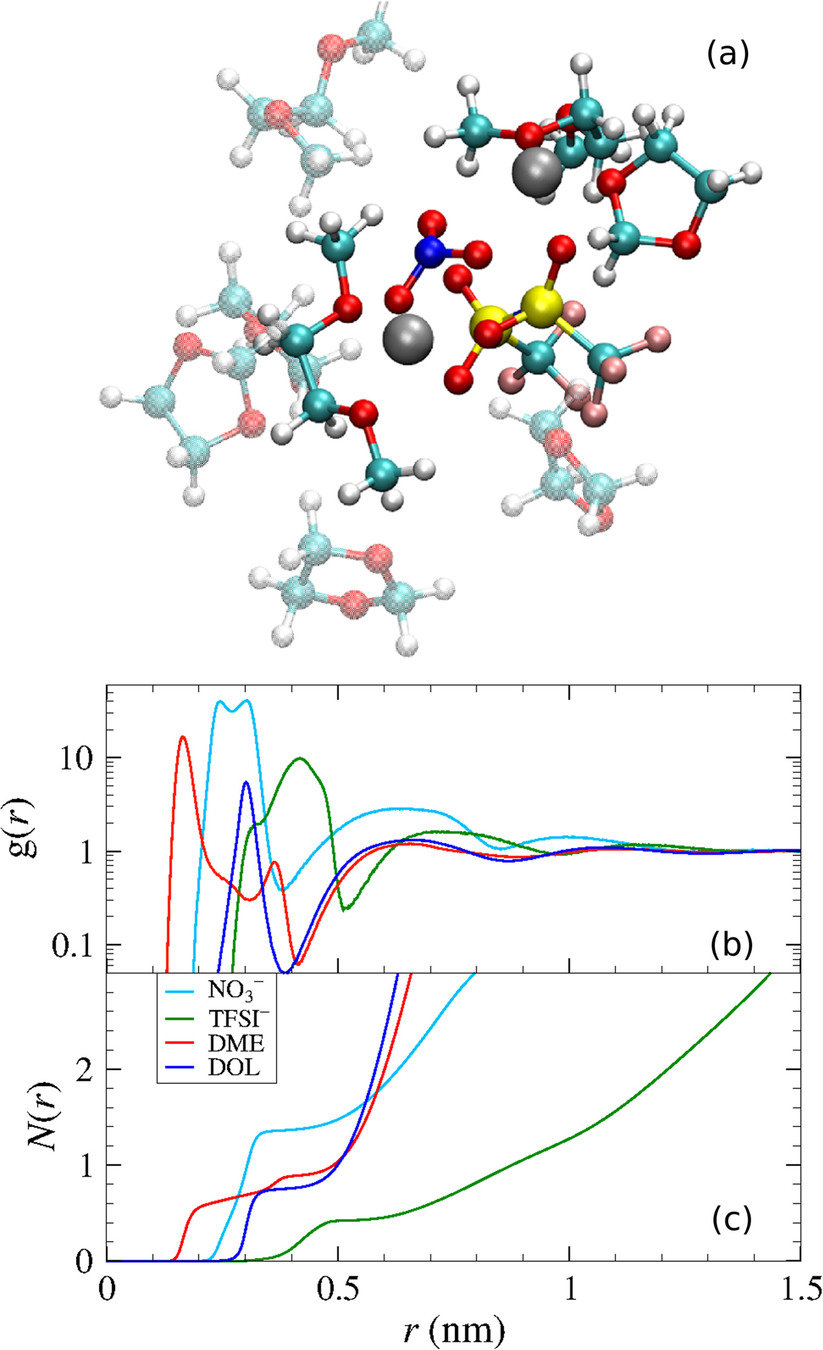
Park, C.; et al. J. Power Sources 2018, 373, 70-78. DOI: 10.1016/j.jpowsour.2017.10.081

Lv, X.; et al. Chem. Phys. Lett. 2018, 706, 237-242. DOI: 10.1016/j.cplett.2018.06.005

Fuel production

Solvation plays an important role

Catalysts

Ma, C.; et al. ACS Catal. 2012, 373, 1500-1506. DOI: 10.1021/cs300350b

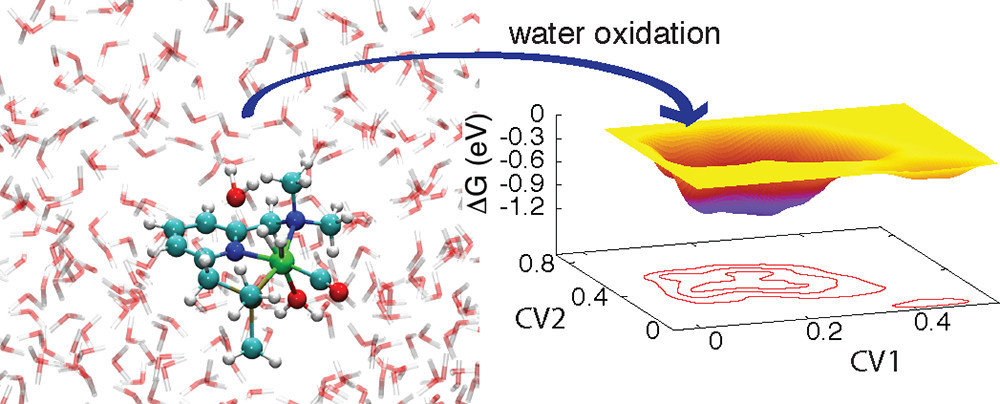
Accelerating exploration with solvents

 Computational modeling

Cost

AIMD

Classical MD

Implicit/explicit

Implicit

Confidence

Cost

Screening

approach

Promising candidates

Search space

without experimental data

Solvation treatments

Confidence requires explicit (MD) methods

Goal

Explicit solvation

Lv, X.; et al. Chem. Phys. Lett. 2018, 706, 237-242. DOI: 10.1016/j.cplett.2018.06.005

Let's model a molten salt

DFT

N^{3-4}

MP2

N^5

CCSD(T)

N^7

Pro: Fast

Con: Parameters

Classical potential

Quantum chemistry

Pro: Accurate

Con: Cost

We need a new method

Confidence

2x atoms

128x cost

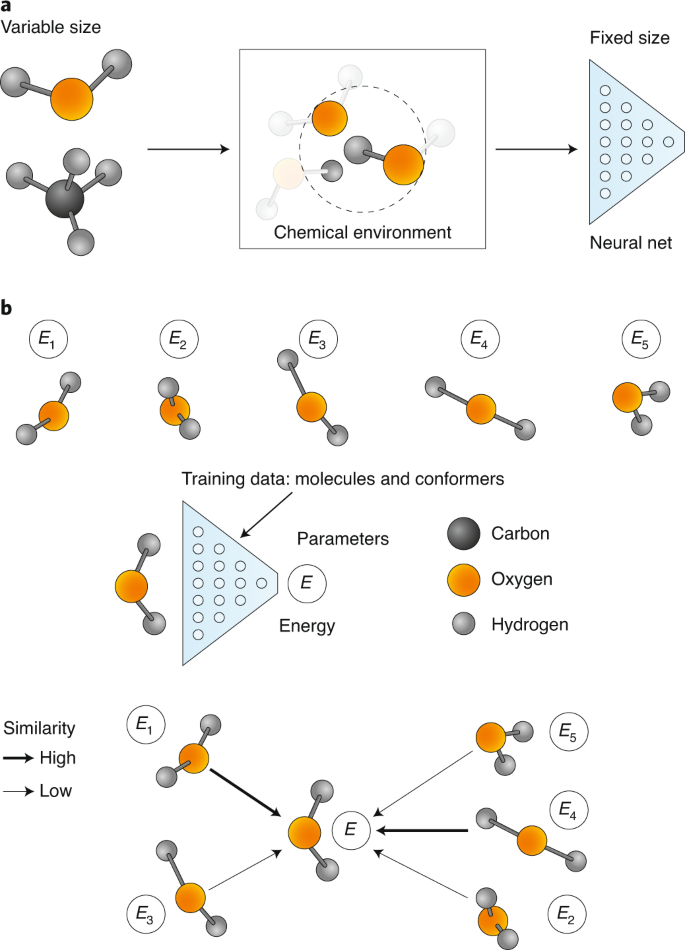
Machine learning potentials

Structure

ML potential

Energy and forces

Quantum

chemistry

Machine learning potentials

Calculate total energies with QC

Training a typical ML potential

Sample tens of thousands of configurations

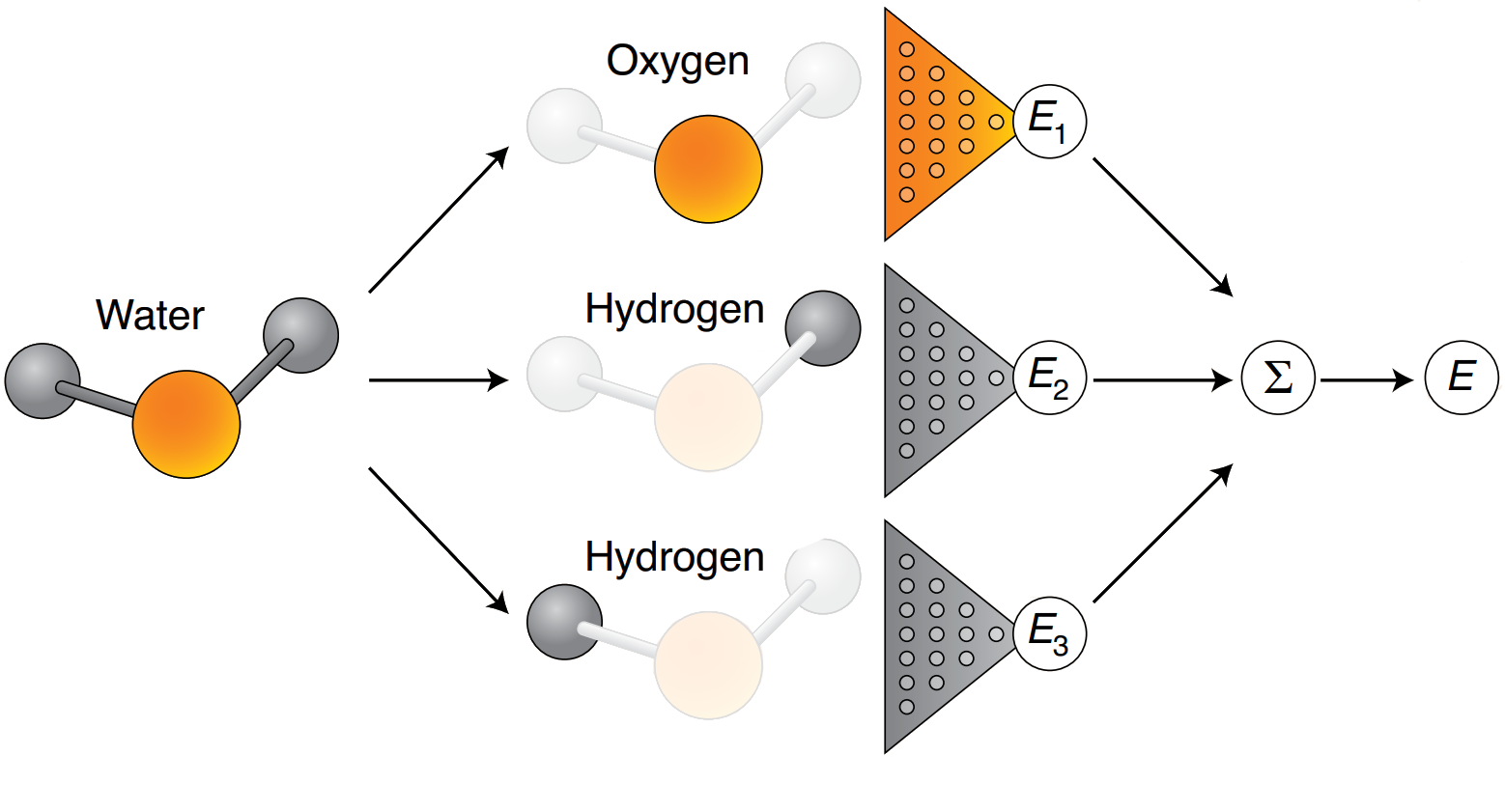
Approximation:  atomic contributions can reproduce total energy 

Examples: DeePMD, GAP, SchNet, PhysNet, ANI, . . .

E_{total} \approx \sum\limits^{N_{atoms}} \varepsilon_i

Known

Learned

with a local descriptor

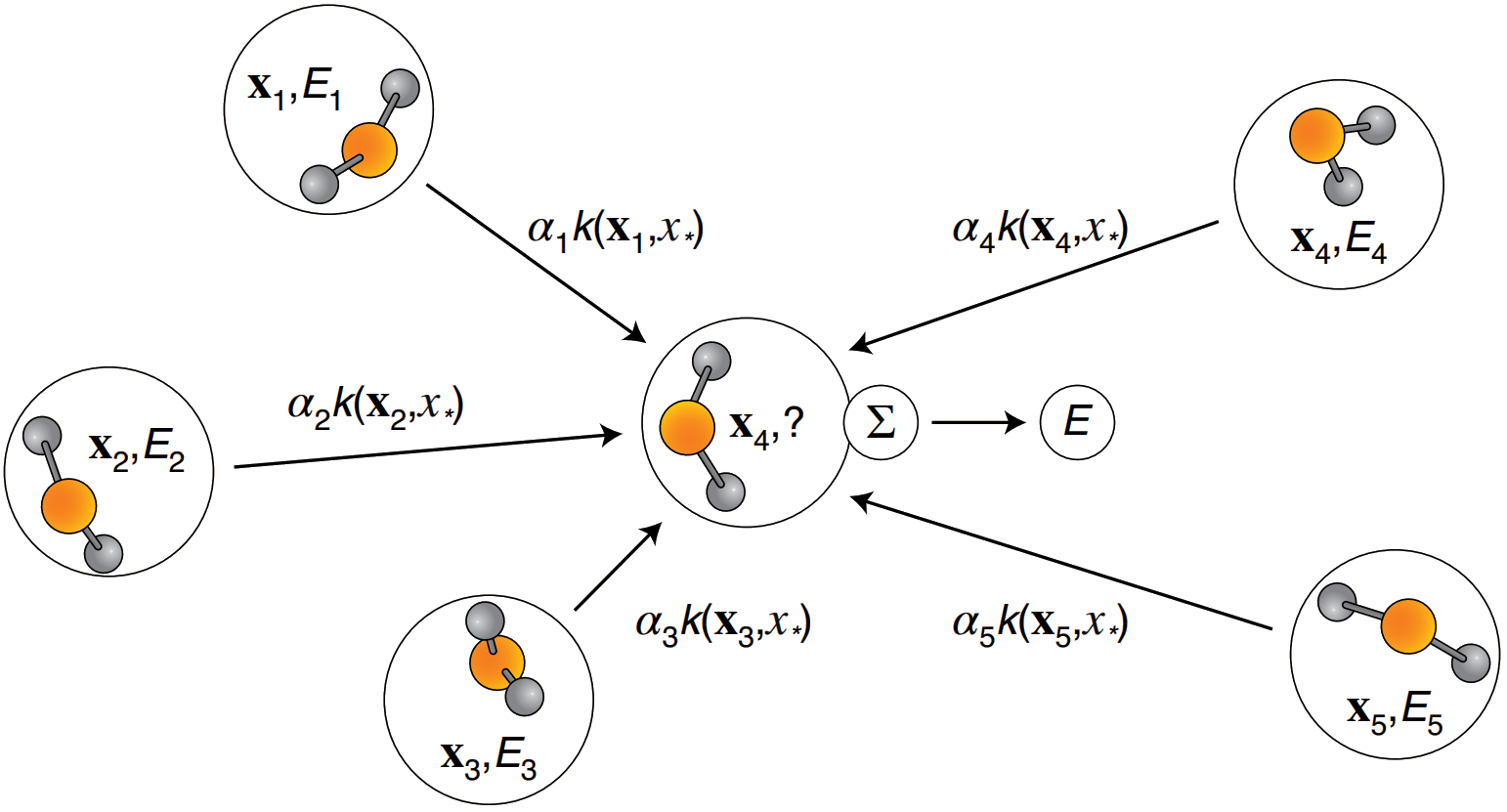
Machine learning potentials

Training with a global descriptor

Local

Global

Encodes each

atom

Encodes entire

structure

increased data efficiency

Many descriptors and parameters

Single descriptor

Machine learning potentials

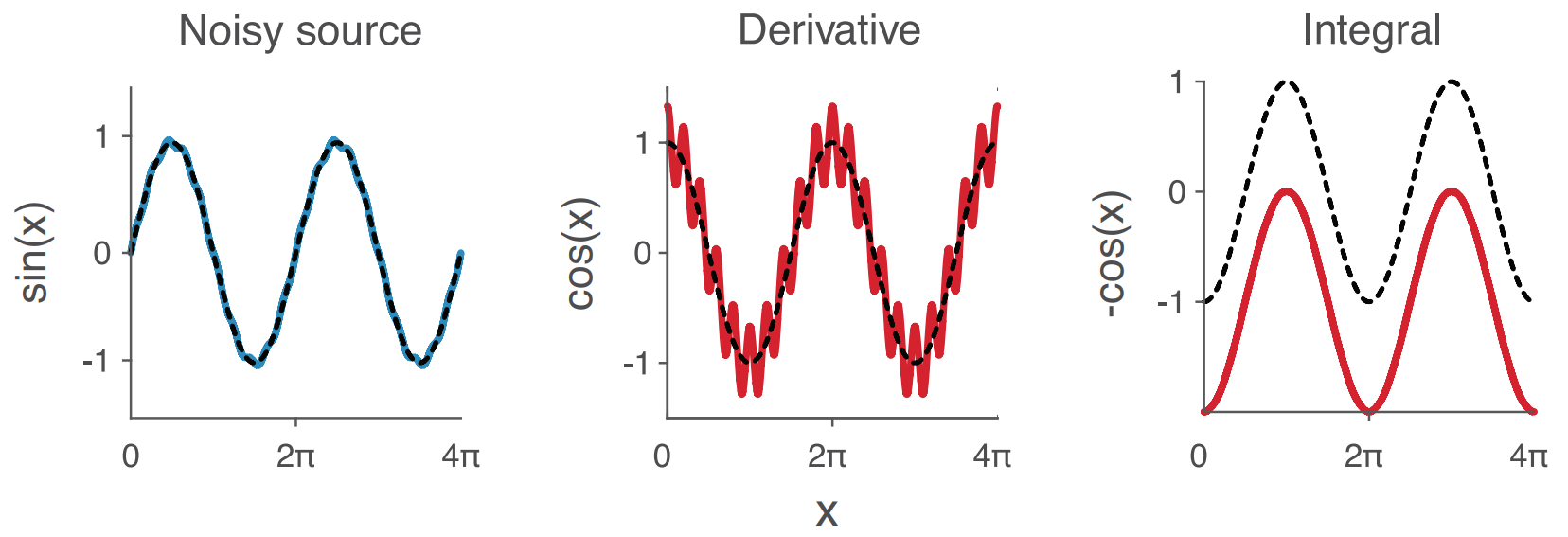
Training on forces provides more information about the geometry and energy relationship

Chimiela, S. ; et al. Sci. Adv. 2017, 3 (5), e1603015. DOI: 10.1126/sciadv.1603015

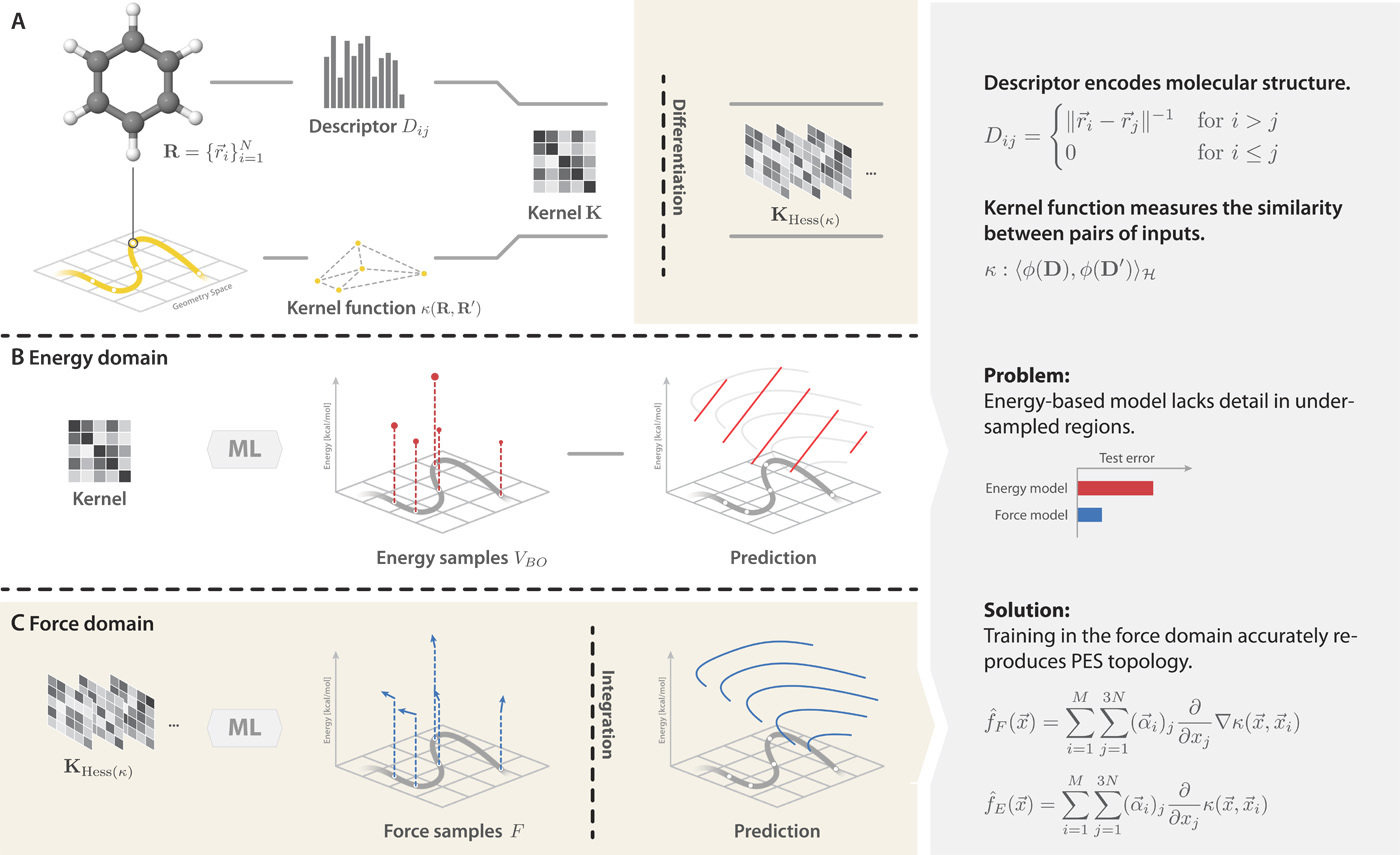
Gradient-domain machine learning (GDML)

Better interpolation

Global descriptor

Training on forces

+

requires 1 000 structures instead of 10 000+

=

Machine learning potentials

System size is still a limiting factor

Global

Fewer structures enables higher levels of theory

CCSD(T)

CCSD(T)

Local

No

Tons of sampling

CCSD(T)

What we want

What we can afford

Descriptor

Size transferable?

CCSD(T)

How can we make GDML potentials size transferable?

Transferability with n-body interactions

-76.31270

-76.31251

-76.31273

-228.96298

-0.00831

-0.00705

-0.00700

-228.93794

(-0.02504)

-228.96031

(-0.00267)

1 body

1+2 body

3-body

+

+

=

+

+

=

Add energy

Remove energy

All energies are in Hartrees

Many-body expansion (MBE)

MBE: the total energy of a system is equal to the sum of all n-body interactions

Truncate

E =
\sum E_i^{(1)}
\sum\Delta E_{ij}^{(2)}
\sum \Delta E_{ijk}^{(3)}
+ \cdots
+
+

Unlocks size transferability for highly accurate methods

CCSD(T)

Many-body expansion (MBE)

Training a many-body GDML (mbGDML) potential

Sample a thousand

configurations

Calculate n-body energy (+ forces) with QC

Calculate total energies with QC

Known

E_{total} \approx \sum E_i^{(1)} + \sum\Delta E_{ij}^{(2)} + \sum \Delta E_{ijk}^{(3)}
E_{total} \approx \sum\limits^{N_{atoms}} \varepsilon_i

Known

Learned

Reproduce physical n-body energies

Approximation:  atomic contributions can reproduce total energy 

Incorporates more physics into our ML potentials

Sample tens of thousands of configurations

Our innovation

  • Less training data
  • Use higher levels of theory
  • Easy to parallelize

Many-body expansion framework accelerated with GDML

Unique opportunity with GDML accuracy and efficiency

If successful

keithgroup.github.io/mbGDML/

Case study

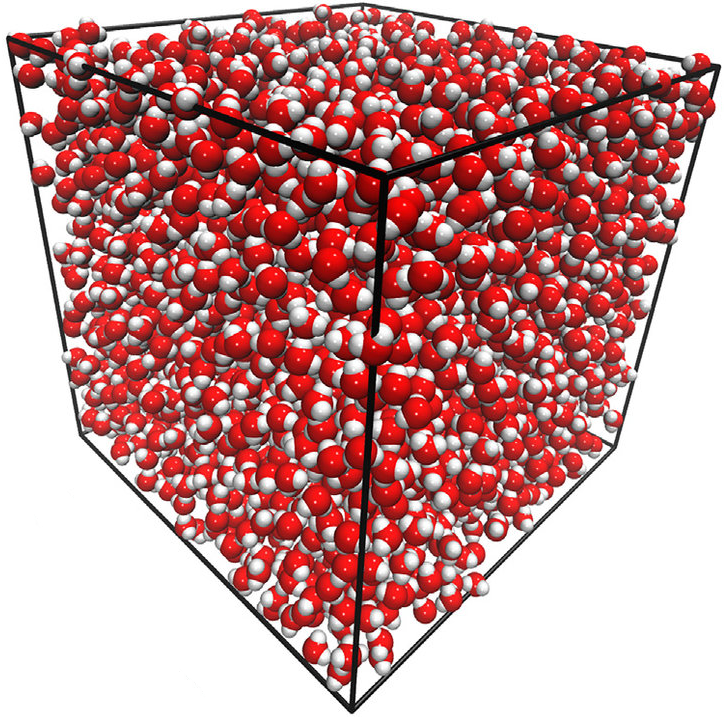
Modeling three common solvents

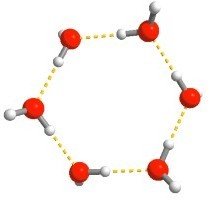
Water (H2O)

Acetonitrile (MeCN)

Methanol (MeOH)

Training set

1 000 structures

(instead of 10 000+)

Sampling

n-body structures from GFN2-xTB simulations

Level of theory

MP2/def2-TZVP

ORCA v4.2.0

Case study - Results

Isomer rankings

Which tetramer (4mer) has the lowest energy (i.e., global minimum)?

Requires accurate relative energies

Isomer #1

Isomer #2

Isomer #3

Case study - Results

Tetramer rankings

(per monomer)

System Energy RMSE [kcal/mol] Force RMSE [kcal/(mol A)]
(H2O)4 0.82 (0.20)
 0.78 (0.07)
(MeCN)4 0.29 (0.07) 0.16 (0.01)
(MeOH)4 1.37 (0.34) 1.49 (0.06)

(per atom)

Many-body GDML accurately captures relative energies

Info: We desire methods with less than 2 kcal/mol error

Does mbGDML scale to larger systems?

System Energy Error [kcal/mol] Force RMSE [kcal/(mol A)]
(H2O)16  4.01 (0.25) 1.12 (0.02)
(MeCN)16 0.28 (0.02) 0.35 (0.004)
(MeOH)16 5.56 (0.35) 1.79 (0.02)

Case study - Results

Consistent normalized errors

Size transferable

Case study - Results

Radial distribution function (rdf)

What we want

r

g(r)

Tells us if we are getting the correct liquid structure

Case study - Results

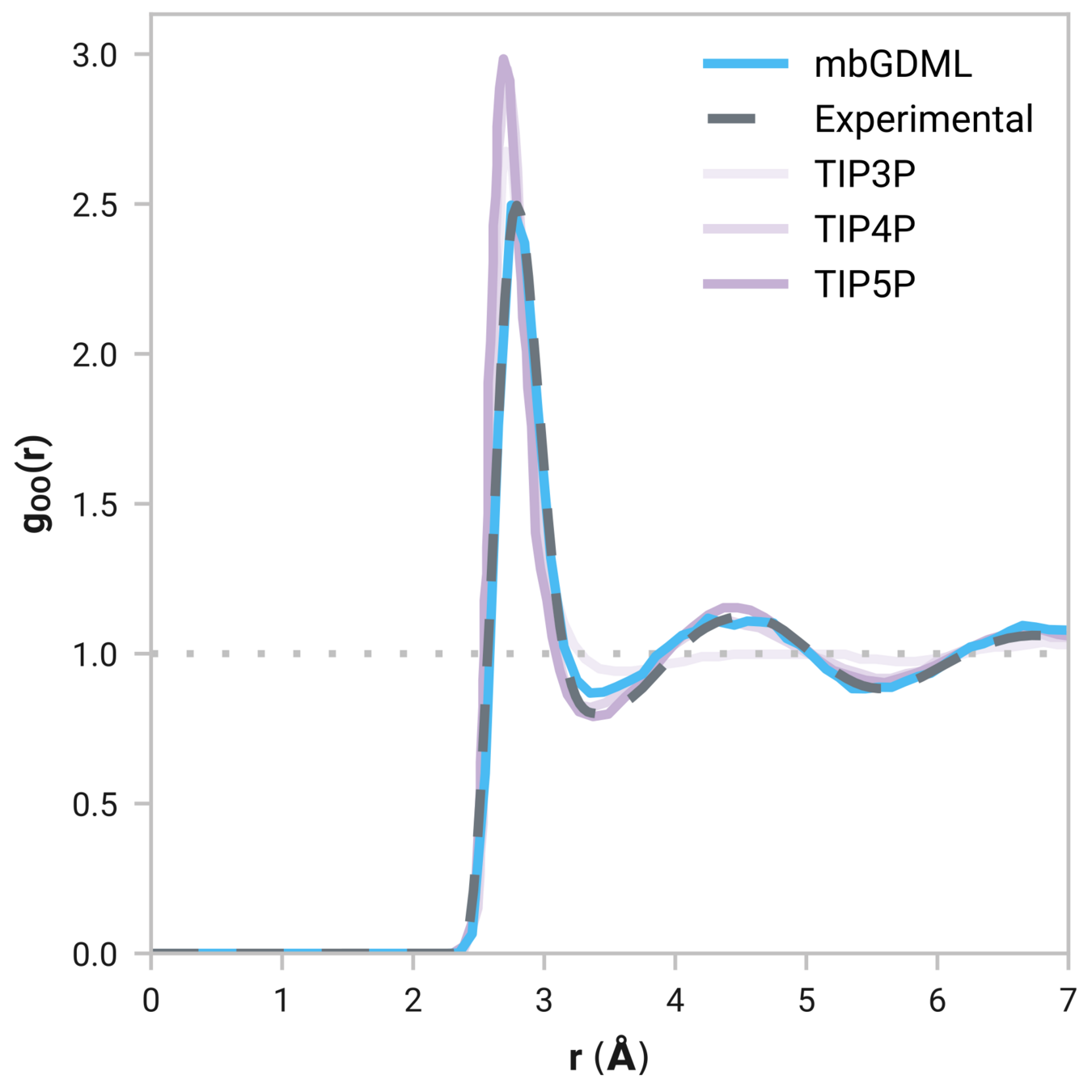
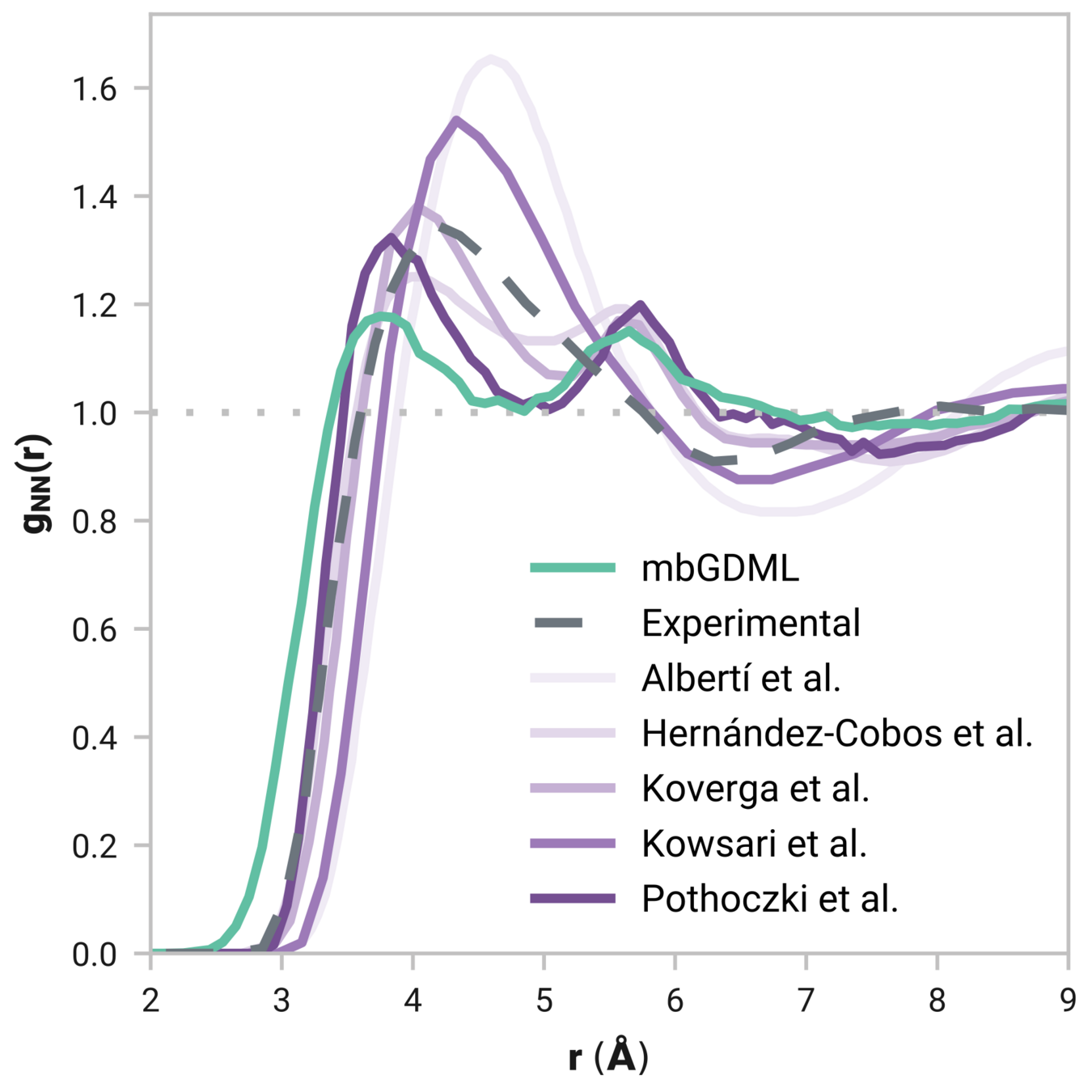
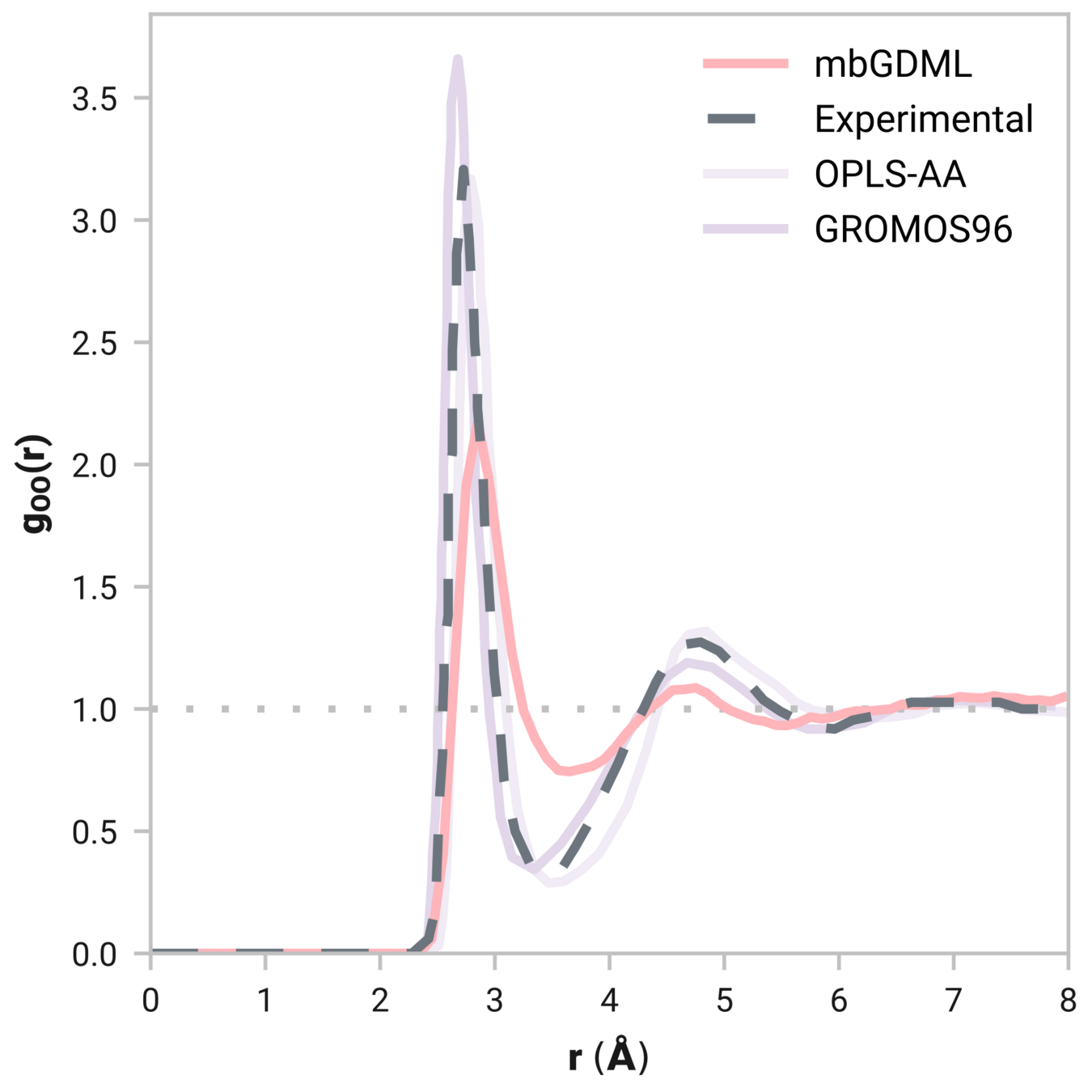
Many-body GDML accurately captures liquid structure

137 H2O molecules

67 MeCN molecules

61 MeOH molecules

Reminder: We have only trained on clusters with up to three molecules

Time for 10 ps MeCN simulation:

mbGDML     19 hours

\approx

MP2      23 762 years

\approx

20 ps NVT MD simulations; 1 fs time step; Berendsen thermostat at 298 K

Conclusions

Explicit solvent modeling without experimental data

Classical

Ab initio

ML

mbGDML

Training

Speed

Accuracy

Scaling

Poor

Excellent

Acknowledgments

InSiDe ChEMS group

Dr. John Keith

Dr. Yasemin Basdogan

Dr. Charles Griego

Dr. Emily Eikey

Lingyan Zhao

Barbaro Zulueta

Chinmay Mhatre

Dominick Filonowich

Funding

Office of the Provost

Solvent effects

Modeling in the absence of experimental data

Implicit

Explicit

Implicit/Explicit

Explicit modeling is required for confident predictions

Maldonado, A. M. ; et al. J. Phys. Chem. A. 2021, 125 (1), 154-164. DOI: 10.1021/acs.jpca.0c08961

Global descriptor: inverse pairwise distances

GDML is a highly accurate and efficient ML potential

Gradient-domain machine learning (GDML)

Learns: relationship between structure and atomic forces

Chimiela, S. ; et al. Sci. Adv. 2017, 3 (5), e1603015. DOI: 10.1126/sciadv.1603015

Performance: sub kcal/mol accuracy on 1,000 training structure

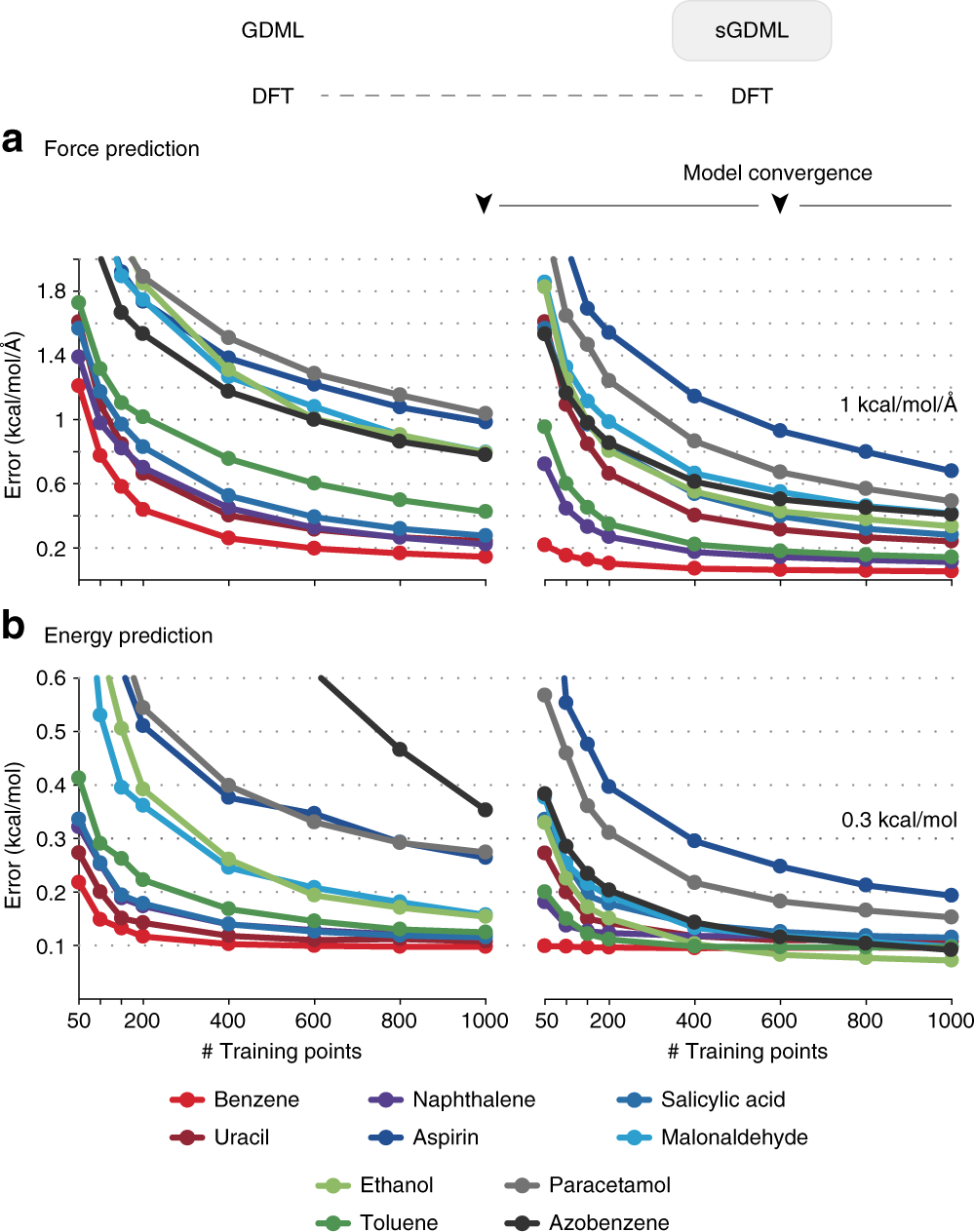
No symmetries

Symmetries

Chmiela, S. ; et al. Nat. Commun. 2018, 9 (1), 3887. DOI: 10.1038/s41467-018-06169-2

Machine learning potentials

Closing the gap between ab initio accuracy and classical efficiency

Ab initio accurate

Classical efficient

Machine learning

Many-body GDML

Specifying many-body system

entity_ids: integers that assign an atom to an entity (i.e., molecule, material, functional group)

z: Atomic numbers of all atoms in the system

R: Cartesian coordinates of all atoms

[8, 1, 1, 8, 1, 6, 1, 1, 1]

H2O

MeOH

comp_ids: labels that assigned to each entity for model identification

[[ -0.93996,  -0.73423,  -0.91605],
   -0.64198,  -0.63683,   0.00659],
   -0.40197,  -0.12512,  -1.34936],
    9.26385,  -2.64576,  -0.31342],
    9.47745,  -1.80746,   0.18550],
    7.82122,  -2.82878,  -0.46631],
    7.21722,  -1.88002,  -0.42174],
    7.43501,  -3.56731,   0.30104],
    7.54895,  -3.05498,  -1.46330]]

H2O

MeOH

['h2o', 'meoh']

H2O

MeOH

[0, 0, 0, 1, 1, 1, 1, 1]

H2O

MeOH

Many-body GDML

Driving many-body predictions

Model

n-body energy & force predictions

Parallel workers

Predictor

Customizable

n-body

predictions

+

n+1

n-body combinations generator

Total energy and forces

\sum

Model

n-body energy & force predictions

Parallel workers

Predictor

Customizable

n-body

predictions

+

n+1

n-body combinations generator

Total energy and forces

\sum

Case study - Methods

MBE distance-based screening

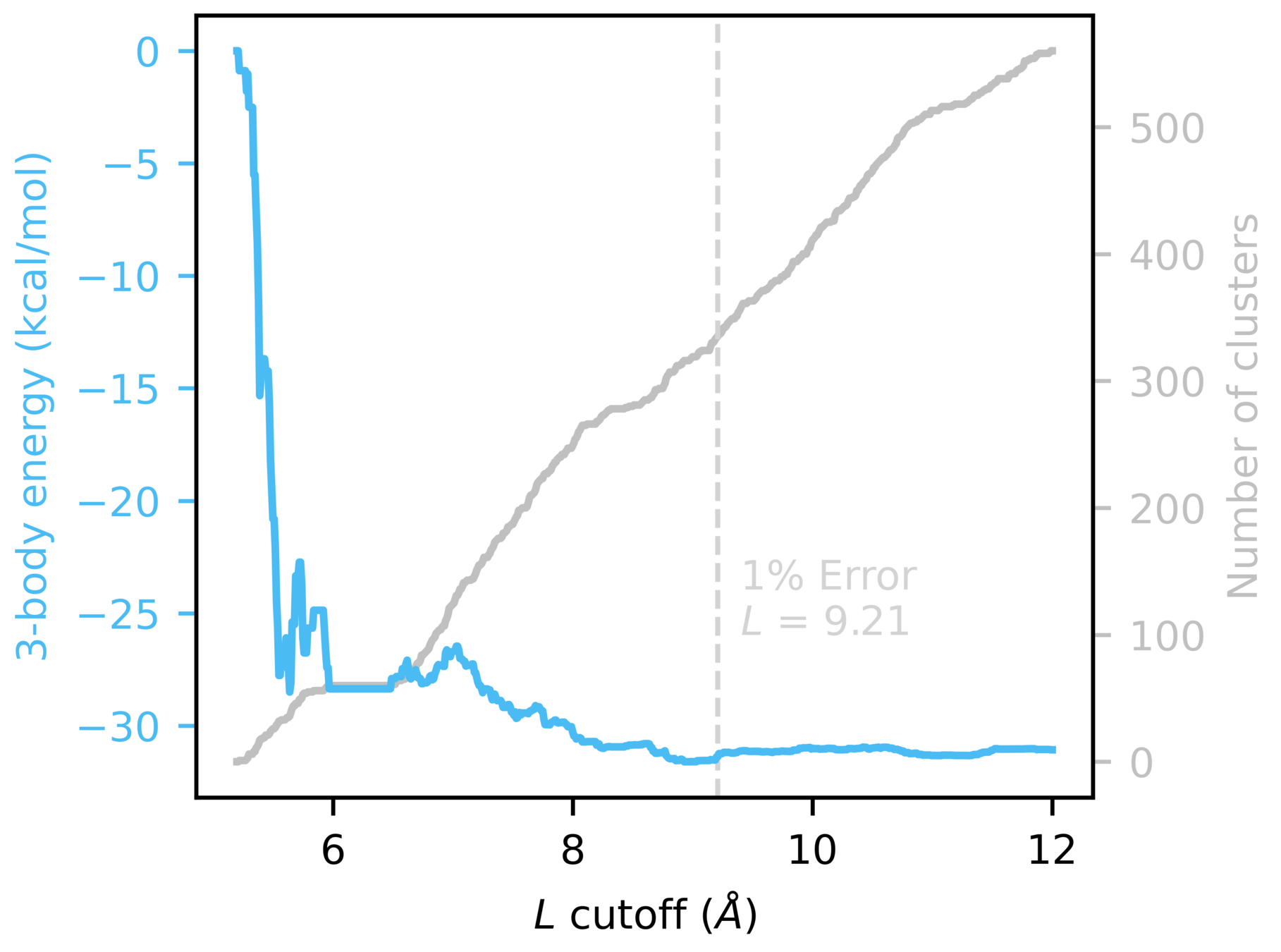
Focus predictions on clusters with meaningful n-body contributions

L = \sum l_i

Training ML potentials

Methods:

GDML

Training set:

1,000 structures

l_1
l_2
l_3

Used 16mer to determine 2- and 3-body cutoffs

Many-body GDML

Developed a Python package for creating, using, and analyzing many-body ML potentials

Supported ML potentials:
GDML, SchNet, GAP

Interfaced with ASE

Extensive documentation

Parallelized with Ray

Archived on Zenodo

Motivation

Solvated reaction mechanisms

For example, reduction of carbon dioxide with sodium borohydride

Explicit local environments are necessary for accurate predictions

Typical for our systems of interest

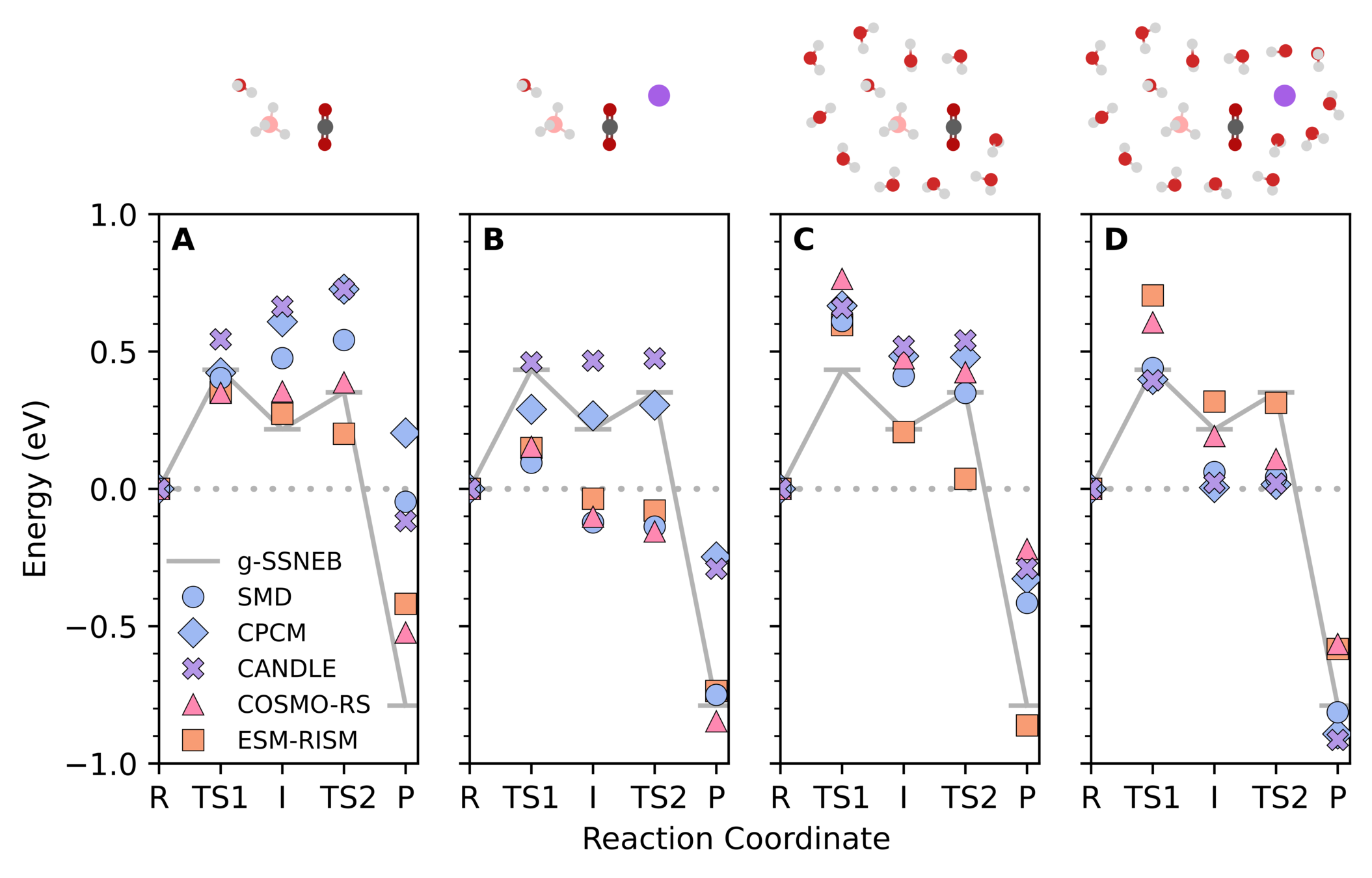
Maldonado, A. M.; et al. J. Phys. Chem. A 2021, 125 (1), 154-164. DOI: 10.1021/acs.jpca.0c08961

Local descriptor

Machine learning potentials

ML potential descriptors require thousands of total energy (+ force) evaluations to train

Global descriptor

Friederich, P. ; et al. Nat. Mater. 2021, 20 (6), 750-761. DOI: 10.1038/s41563-020-0777-6

Case study - ML potential

Gradient-domain machine learning (GDML) learns the relationship between atomic structure and forces

Chimiela, S. ; et al. Sci. Adv. 2017, 3 (5), e1603015. DOI: 10.1126/sciadv.1603015

Training set

1,000 structures

(~10x less than most ML potentials)

Validation set

2,000 structures

Sampling

Semiempirical QC MD simulations

Why not train ML potential on total energies of small clusters?

System Size Many-body Energy MAE Standard Energy MAE
(MeOH)4 2.59  (0.65) 11.00  (2.75)
(MeOH)5 3.30  (0.66) 18.78  (3.76)
(MeOH)6 3.75  (0.63) 22.81  (3.80)
(MeOH)16 3.42  (0.21) 53.36  (3.34)

Case study - Results

Train SchNet potential on 1mer, 2mer, and 3mer energies

There are limitations on size transferabilities of local descriptors

Avoids combinatorics of many-body expansions

(per monomer)

SOAP descriptor

Smooth overlap of atomic positions

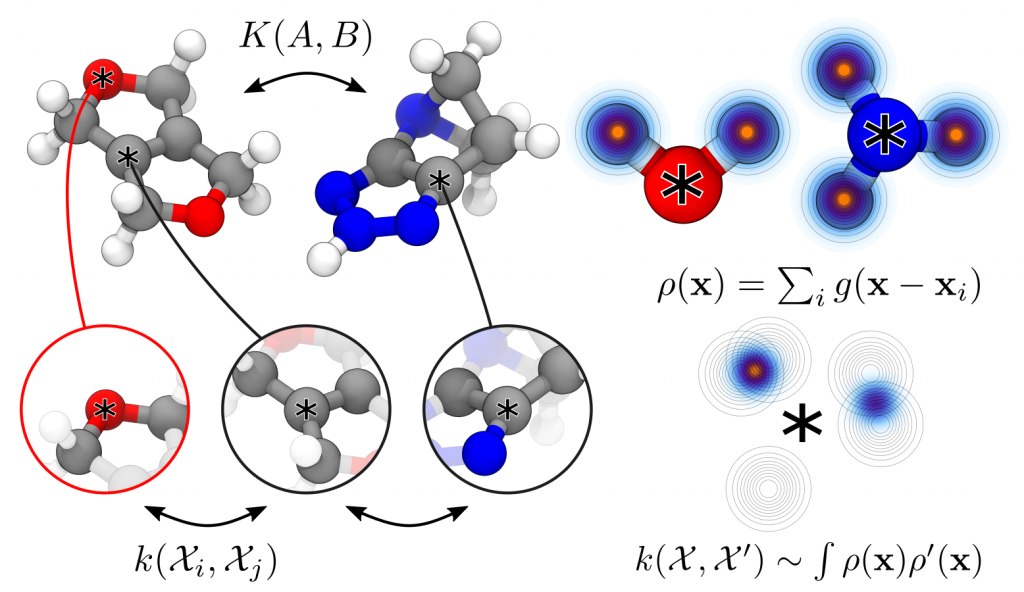
Neural network potential

High-dimensional neural network potential

Case study - Results

Isomer rankings

(per monomer)

Size Energy RMSE [kcal/mol] Force RMSE [kcal/(mol A)]
4mer 0.82 (0.20) 0.78 (0.07)
5mer 1.12 (0.22) 0.91 (0.06)
6mer 1.80 (0.30) 1.26 (0.07)

(per atom)

mbGDML accurately predicts global minimum for water isomers

Case study - Results

Isomer rankings

(per monomer)

Size Energy RMSE [kcal/mol] Force RMSE [kcal/(mol A)]
4mer 0.29 (0.07) 0.16 (0.01)
5mer 0.33 (0.07) 0.22 (0.01)
6mer 0.34 (0.06) 0.24 (0.01)

(per atom)

mbGDML is only as good as many-body expansions

Several low-lying isomers within 1 kcal/mol

Isomer rankings

Case study - Results

(per monomer)

Size Energy RMSE [kcal/mol] Force RMSE [kcal/(mol A)]
4mer 1.37 (0.34) 1.49 (0.06)
5mer 1.87 (0.37) 1.77 (0.06)
6mer 2.29 (0.38) 1.73 (0.05)

(per atom)

Higher-order contributions mainly impact absolute energies