小社賽題解

problem setter:
AaronWu

BrineTw

IvanLo

Repkironca

比賽結果

Aaw will never find that 

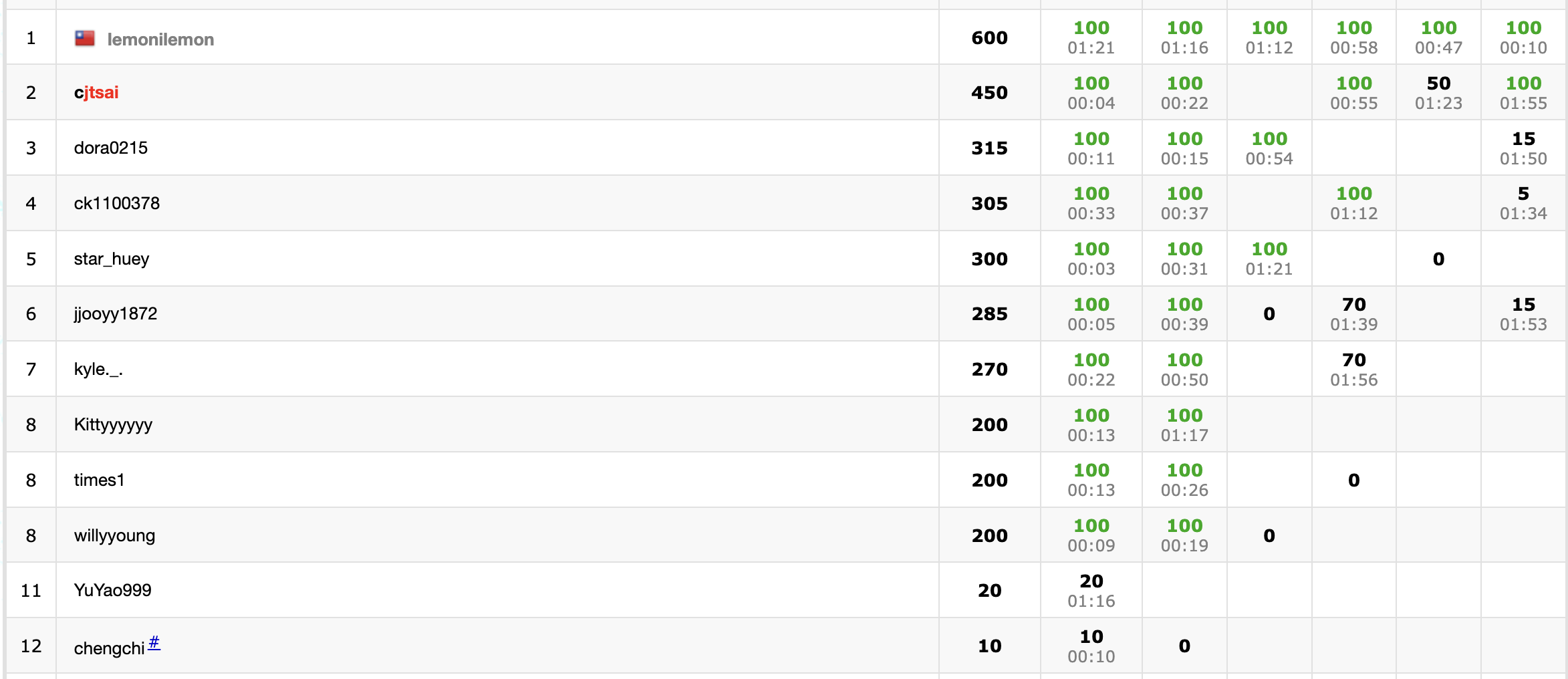
名次

  1. cjtsai (450)
  2. dora0215 (315)
  3. star_huey (300)
  4. jjooyy1872(285)

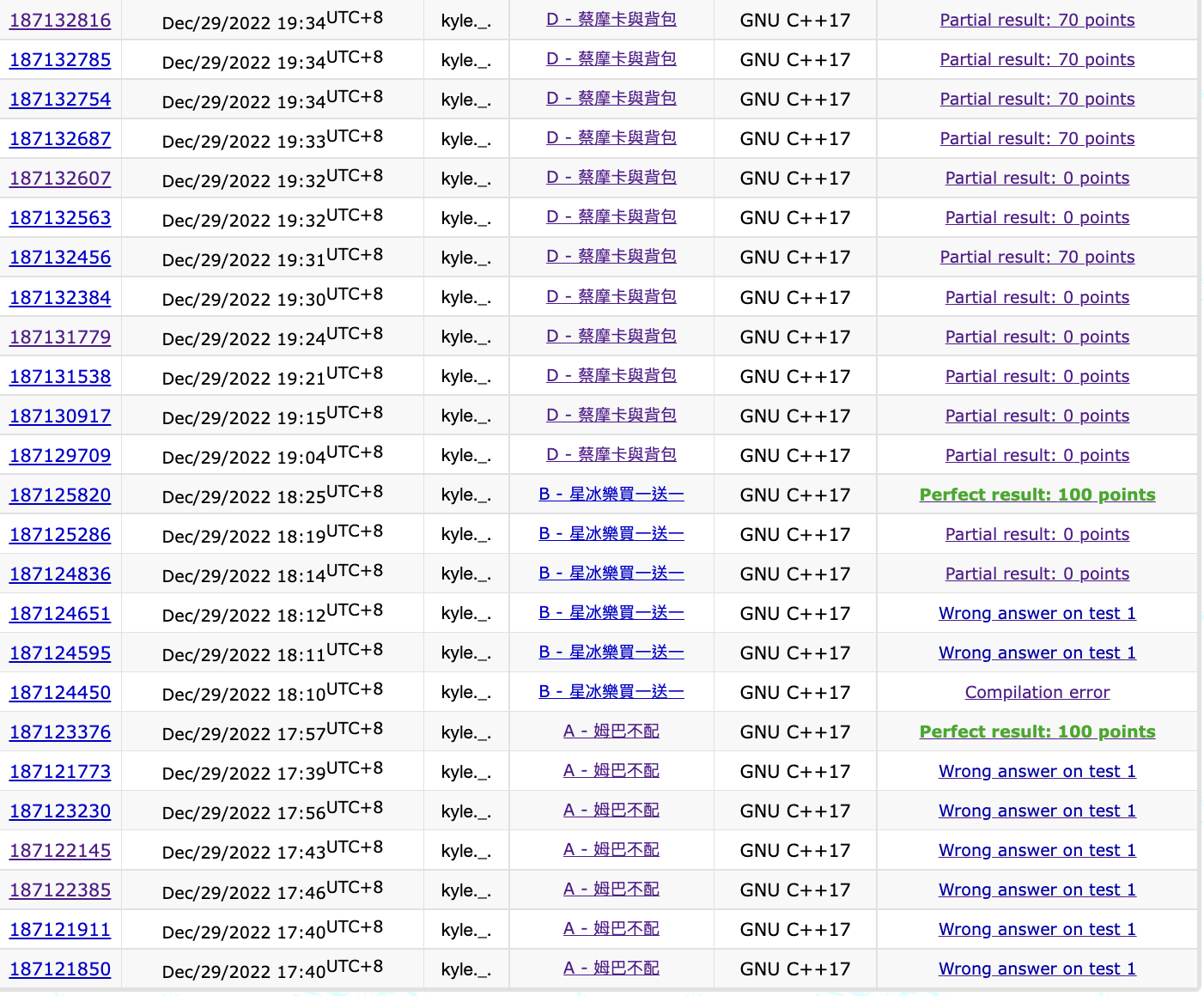
最會亂submit獎

如果這場比賽有penalty你一定吃爆

kyle._.

惜submit如金獎

如果這場比賽有penalty你一定賺爆

每發必中誒超強

kittyyyyyy

pA

姆巴不配

簡單來說

其實就是計算己方球員跟敵方球員

相對於底線的距離，

如果己方球員離底線較近則輸出Yes

反之則輸出No

#include <iostream>
int main(){
    int x, y;
    while(std::cin >> x >> y){
        x < y ? std::cout << "Yes\n" : std::cout << "No\n";
    }
    return 0;
}

AC扣

pB

這題的定位是一題水題

星冰樂買一送一

大部分人都有寫出來，還不錯啦

# PRESENTING CODE
  • 這題就是上課時有講過的陣列刪除
  • 蛤？你說你沒上過課？：簡報連結
  • 簡單講：
    • 按照Greedy的想法，選擇前n/2杯便宜的一定最好。另外按照紅白球的思維，你可以發覺這件事我們一定辦得到
  • 這題的注意事項：
    • sort 要會寫
    • 要記得開 long long !!!

AC code在這裡

# AC code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
 
signed main() {
    ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int n;
    cin >> n;
    vector<int> arr(n);
 
    for (auto &i : arr) cin >> i;
    sort(arr.begin(), arr.end());
    ll ans = 0;
    for (int i = 0; i < n/2; ++i) {
        ans += arr[i];
    }
    cout << ans << "\n";
}

用priority_queue的寫法

# TLE code
#include<bits/stdc++.h>
#define ll long long
using namespace std;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n, temp;
    cin >> n;
    priority_queue<ll, vector<ll>, greater<ll> > s;
    for(int i=0; i<n; i++){
        cin >> temp;
        s.push(temp);
    }

    ll sum =0;
    for (int i = 0; i < n/2; i++){
        sum += s.top();
        s.pop();
    }
    
    cout << sum;
}

這樣寫沒有很好，但好多人這樣寫w

pC

有人寫我的題目，好開心

覺得題目怎麼樣

  • 看不懂？
  • 不知道怎麼寫？
  • 對不起我沒有教好

連通圖 Connected Graph

  • 如果所有點都是無向邊是否所有點都可以到任意一個點
0
1
3
2
4
0
1
3
2
4

如何檢查圖是否連通

  • 每個點都走得到另外一點
  • 兩點之間距離有限
  • 用 BFS 求出所有點和某一點最短距離
    • 如果能求出最短距離即代表走得到
    • 需要記錄距離嗎？
    • 記錄是否到達！
  • 用 DFS 也可以
    • 是否能用某種方法走完整張圖

小觀察

  • 「只有一種操作，新增一個點並將其連到另一個點上」
  • 「新增一個之前不存在的點 \(u_j\)，該點會透過一條邊連到一個已經出現過的點 \(v_j\)」
  • 每次操作不影響原圖連通與否
  • 每次操作中新的點必定會連到原圖每個點
  • 只要原本圖連通，接下來怎麼操作都是連通的
    • 不用管怎麼操作內容！

Solution

  • 也不是不能用並查集？
#include <bits/stdc++.h>

using namespace std;

void dfs(int u, vector< vector<int> >& graph, vector<bool>& visited) {
    visited[u] = 1;

    for (auto& v: graph[u]) {
        if (visited[v]) continue;

        dfs(v, graph, visited);
    }
}

int main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    int n, m;
    cin >> n >> m;

    vector< vector<int> > graph(n);

    int u, v;
    for (int i = 0; i < m; i++) {
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u);
    }

    vector<bool> visited(n);

    dfs(0, graph, visited);

    bool flag = 1;

    for (int i = 0; i < n && flag; i++) {
        flag = visited[i];
    }

    int q;
    cin >> q;

    for (int i = 0; i < q; i++) {
        cout << (flag ? "No\n" : "Yes\n");
    }
}

把變數放外面的 DFS

  • 我討厭全域變數
#include <bits/stdc++.h>

using namespace std;

vector< vector<int> > graph;
vector<bool> visited;

void dfs(int u) {
    visited[u] = 1;

    for (auto& v: graph[u]) {
        if (visited[v]) continue;

        dfs(v, graph, visited);
    }
}

int main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    int n, m;
    cin >> n >> m;

    graph.resize(n);

    int u, v;
    for (int i = 0; i < m; i++) {
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u);
    }

    visited.resize(n);

    dfs(0);

    bool flag = 1;

    for (int i = 0; i < n && flag; i++) {
        flag = visited[i];
    }

    int q;
    cin >> q;

    for (int i = 0; i < q; i++) {
        cout << (flag ? "No\n" : "Yes\n");
    }
}

Lambda DFS

  • 我是毒瘤
#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    int n, m;
    cin >> n >> m;

    vector< vector<int> > graph(n);

    int u, v;
    for (int i = 0; i < m; i++) {
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u);
    }

    vector<bool> visited(n);

    function<void(int)> dfs = [&](int u) {
        visited[u] = 1;

        for (auto& v: graph[u]) {
            if (!visited[v]) dfs(v);
        }
    };

    dfs(0);

    bool flag = 1;

    for (int i = 0; i < n && flag; i++) {
        flag = visited[i];
    }

    int q;
    cin >> q;

    for (int i = 0; i < q; i++) {
        cout << (flag ? "No\n" : "Yes\n");
    }
}

鞭   屍

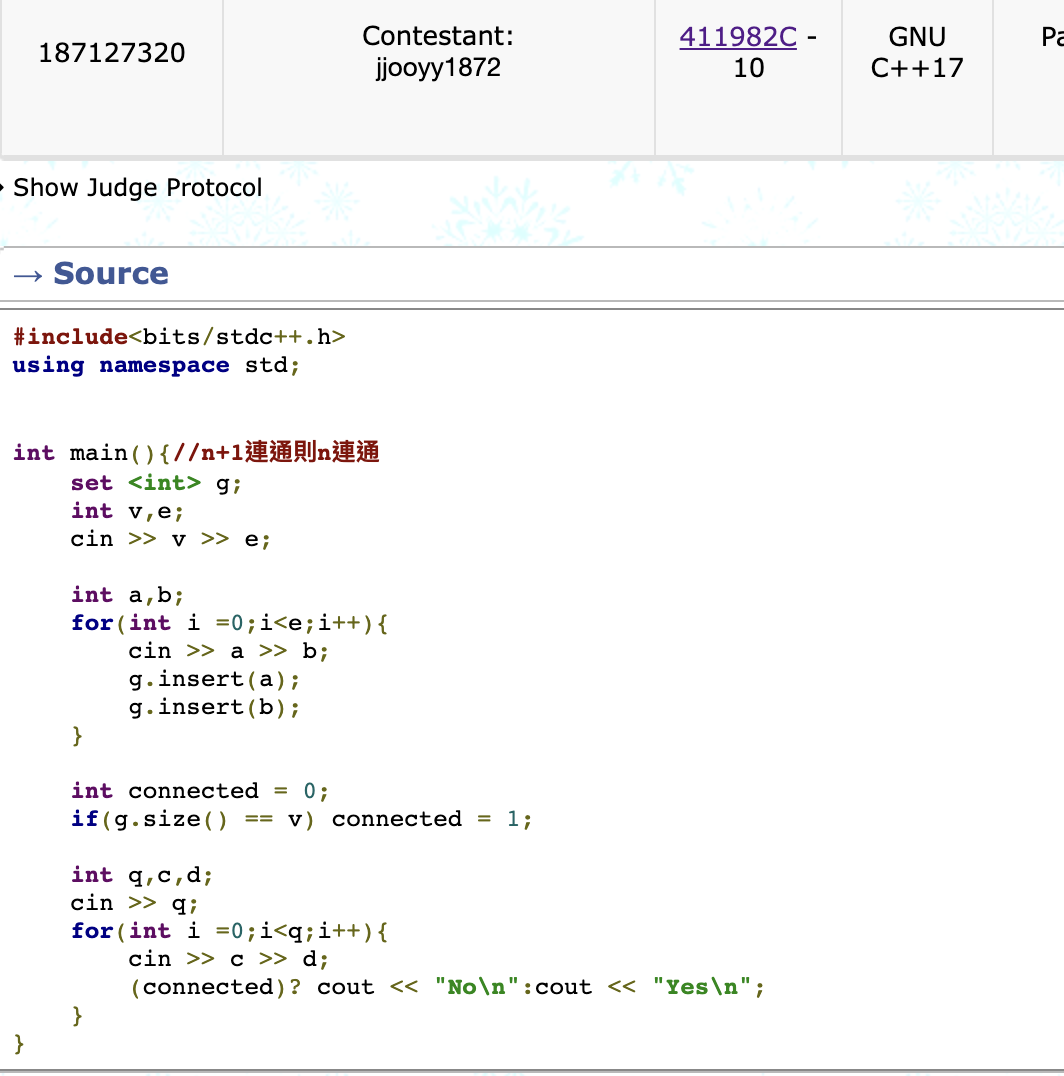
MR 的假解

（竟然差點沒有卡掉)

pD

這題就只是一題背包問題啦

蔡摩卡與背包

看起來大家對背包問題其實不熟...

# PRESENTING CODE

總共n個物品，每個都有特定價值\(v_i\)，而搶救他需花費\(t_i\)的時間，總共不能花超過\(m\)的時間

可以發覺所謂的時間，其實就對應原本背包問題的重量！

但是...魔鬼藏在細節裡...

測資範圍

# PRESENTING CODE

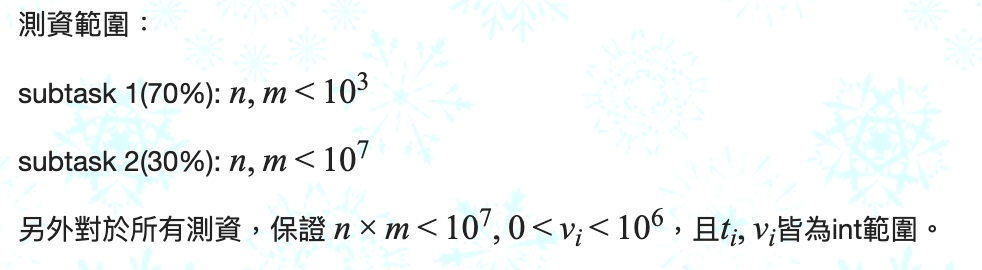
先看到subtask 1，我們可以發覺我並沒有保證 \(t_i < m\)

也就是說，原本簡報上的那個做法

其實會有問題

原本簡報的code

# PRESENTING CODE
for(int i = 1; i <= n; ++i) {
    int w, p;
    cin >> w >> p; // 輸入重量、價值
    for(int j = 0; j < w; ++j) {
        dp[i][j] = dp[i-1][j]; //放不下所以只能選擇不放
    }
    for(int j = w; j <= m; ++j) { // 記得從w開始
        dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + p); 
    }
}

我們可以看到，第4行的迴圈，如果 w 大於 m

這時候你的dp陣列又只有剛好開到m的話，

你就會吃 RE

(或是RE有可能會顯示成WA或TLE)

這份程式碼只有在保證 \(w < m\) 時才是對的

原本簡報的code

# PRESENTING CODE
for(int i = 1; i <= n; ++i) {
    int w, p;
    cin >> w >> p; // 輸入重量、價值
    for(int j = 0; j < w; ++j) {
        dp[i][j] = dp[i-1][j]; //放不下所以只能選擇不放
    }
    for(int j = w; j <= m; ++j) { // 記得從w開始
        dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + p); 
    }
}

不過因為我抄學長簡報

所以我原本沒注意到這個錯w

所以賽中有人改開全域變數就過的原因是因為陣列一開始就夠大所以不會 index out of bound

所以背包問題到底要怎麼寫

# PRESENTING CODE
for(int i = 1; i <= n; ++i) {
    int w, p;
    cin >> w >> p; // 輸入重量、價值
    for(int j = 0; j < m; ++j) {
    	if (j < w) {
            dp[i][j] = dp[i-1][j]; //放不下所以只能選擇不放
        }
        else {
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + p);
        }
    }
}
# PRESENTING CODE

subtask 1 的完整 code

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define endl '\n'
#define AI(x) begin(x),end(x)
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);

signed main(){_
	int n, m;
	cin >> n >> m;
	vector<ll> v(n+1);
	vector<ll> w(n+1);
	for (int i = 1; i <= n; ++i) cin >> v[i];
	for (int i = 1; i <= n; ++i) cin >> w[i];

	ll vsum = 0;
	for (auto &i : v) vsum+=i;
	
	vector< vector<ll> > dp(n+1, vector<ll>(m+1, 0));

	for (int i = 1; i <= n; ++i) {
		for (int j = 0; j <= m; ++j) {
			if (j < w[i]) {
				dp[i][j] = dp[i-1][j];
			}else{
				dp[i][j] = max(dp[i-1][j - w[i]] + v[i], dp[i-1][j]);
			}
		}	
	}
	cout << vsum - dp[n][m] << endl;



	return 0;
}

不過你會發覺這一份程式碼沒辦法讓你AC

繼續看測資範圍

# PRESENTING CODE

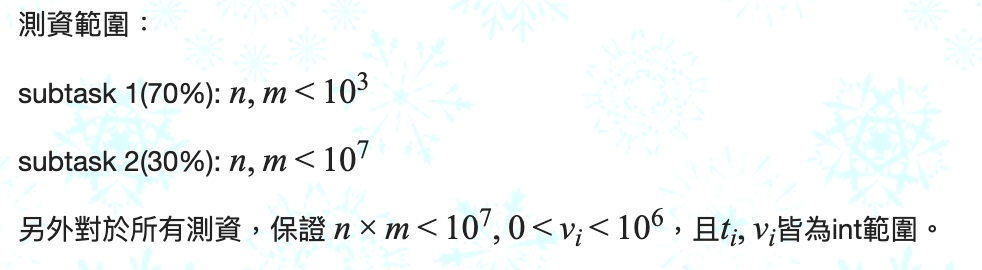
你會發覺，subtask 2 的dp陣列

你開滿一定會吃 MLE

就算你用 vector 也一樣

所以 ...

要用滾動 dp !!!

AC code

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define endl '\n'
#define AI(x) begin(x),end(x)
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);

signed main(){_
	int n, m;
	cin >> n >> m;
	vector<ll> v(n);
	vector<ll> w(n);
	for (auto &i : v) cin >> i;
	for (auto &i : w) cin >> i;
  
	ll vsum = 0;
	for (auto &i : v) vsum+=i; // 儲存總價值
	
	vector<ll> dp(m+5, 0);
	for (int i = 0; i < n; ++i) {
		for (int j = m; j >= w[i]; j--) { // 由上往下
			dp[j] = max(dp[j - w[i]] + v[i], dp[j]);
		}	
	}
	cout << vsum - dp[m] << endl;


	return 0;
}

# PRESENTING CODE

pE

這題其實是防破台題啦哈哈

線段蘇和AaW的心情曲線與被Brine淹沒的島嶼

題序

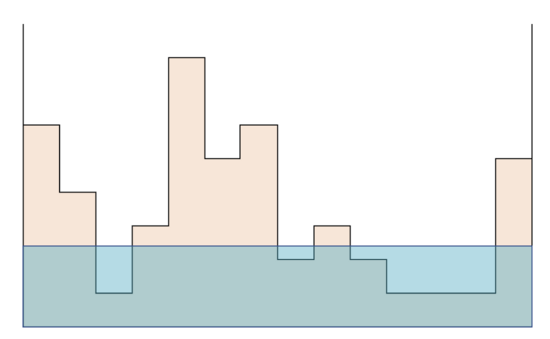
給你一張長這樣的圖，問你可以自由調整水位高度的同時，最多可以淹出幾座島嶼？

嗯，我原本只打算講這樣

# PRESENTING CODE

所以什麼是線段蘇問題

這題其實要分為兩個部分來看

  1. 知道我所謂的線段蘇問題要怎麼解
  2. 通靈出淹水和線段蘇的關聯性
# PRESENTING CODE

所以什麼是線段蘇問題

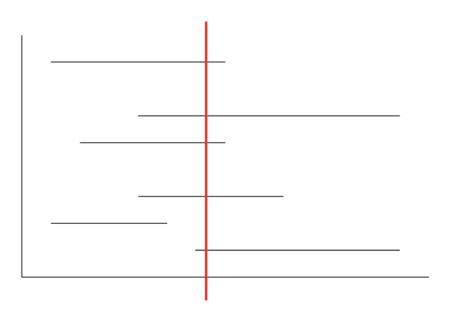
給你很多條線段的左右端點，請你找到一個x座標，使有通過此x座標的線段數目最多，並且輸出線段的數量

# PRESENTING CODE

要怎麼做勒？

先看看暴力做法

窮舉每個x座標，檢查有幾條線段通過

# PRESENTING CODE

複雜度 \(O(nv)\)，其中 \(v\) 為x座標值域

不過我們可以發現一件事

如果我們按x座標順序來檢查

\(i-1\)的線段數目會和 \(i\) 一致，除非...

有線段的其中一端點在\(i\)

所以，我們其實可以只檢查所有有線段端點的x座標就好

但其實，這題應該要壓到\(O(n \log n)\)才會AC

How?

這樣複雜度可以壓到\(O(n^2)\)，subtask 1 會過

（如果看得出淹水和線段蘇的關係的話）

作法：

用一個變數s紀錄當前的線段數，當檢查下一個位置時，

若該點是左端點，則s++

若該點是右端點，則s--

然後另外用一個變數紀錄s曾經出現過的最大值，就是答案了

把所有的端點排序！

# PRESENTING CODE

用一個型態為pair<int, int>的陣列

第一項放x座標，第二項則紀錄左端點或右端點

這樣排序複雜度\(O(n \log n)\)

之後只要照陣列順序進行計算s的值

就可以\(O(n \log n + n)\)的時間複雜度解決線段蘇了

最關鍵的來了

# PRESENTING CODE

淹水和線段蘇的關聯？

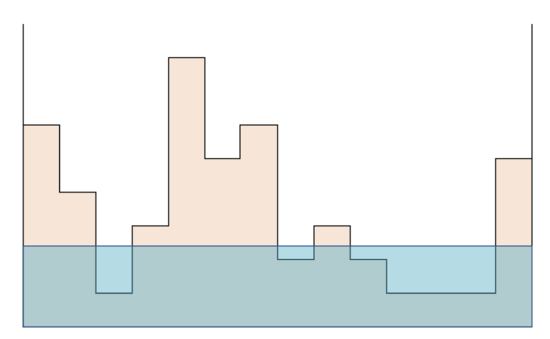
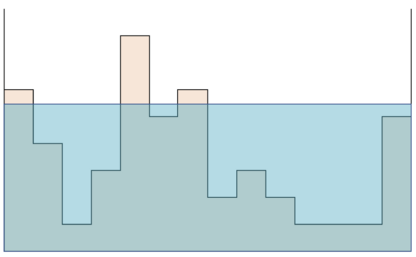
來觀察一下每塊地形成為島嶼，和水位高度的關係？

# PRESENTING CODE

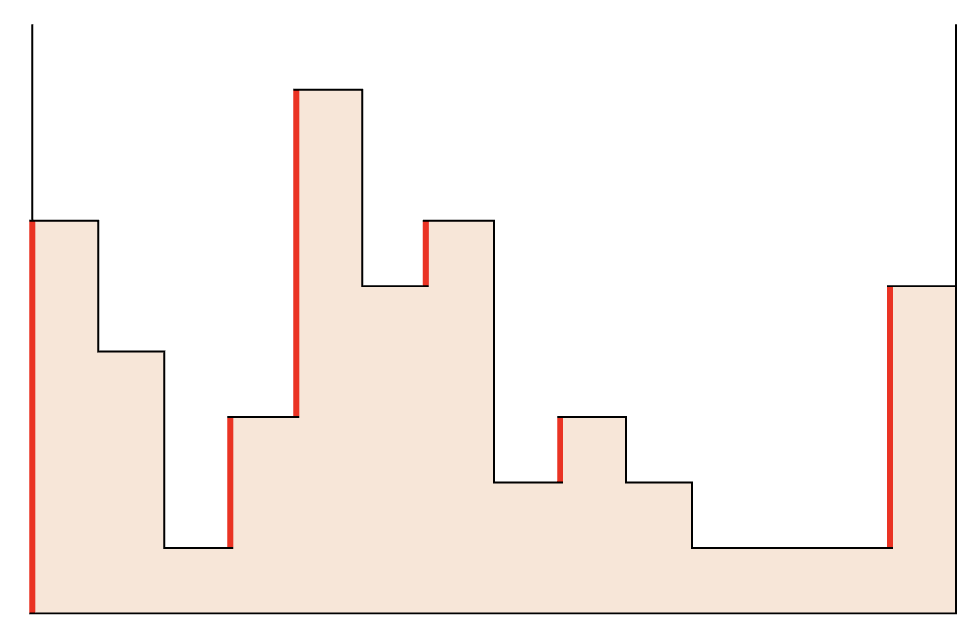
如果我們去看每一個凸起地方的左邊界（你要右邊界也沒差）

你會發覺

當水位高度在這個範圍時，該地形剛好就會是島嶼

而且不會被重複計算到！

# PRESENTING CODE

所以...把這張圖轉九十度

再加上一個可以自由移動的水位線...

線段蘇問題就出現了！

# PRESENTING CODE

不過要注意的是，所有的線段都是左閉右開

因為水位高度和地形高度相同時不算島嶼

# AC CODE

來看官解吧

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
 
 
signed main(){_
    int n;
    cin >> n;
    vector<int> arr(n);
    for (int i = 0; i < n; ++i) {
        cin >> arr[i]; // 輸入地形
    }

    int left = 0;
    vector<pair<int, int>> seg; // 紀錄線段端點的陣列
 
    for (int i = 0; i < n; ++i) {
        if (arr[i] > left) {    // 比較當前位置有沒有比他左邊的高
                                // 有比較高才需要畫線紀錄
            seg.pb({left, 1});    // 線段較低處的開始端點，值為+1（會使線段數增加）
            seg.pb({arr[i], -1}); // 線段較高處的結束端點，值為-1（會使線段數減少）
        }
        left = arr[i];
    }
    
    sort(seg.begin(), seg.end());  // pair預設的sort方式是先比第一項再比第二項

    ll sum = 0, mx = 0;
    for (auto i : seg) {
        sum += i.second;    // 計算經過此端點後的線段數
        mx = max(mx, sum);  // 取答案的max
    }
    cout << mx << '\n';
 
    return 0;
}

pF

Going to the Void

# Dynamic Programming

# 學會不要看阿蘇的題敘

題敘前面都是廢話，我們直接跳過

# Statement

有一張大小為 \(N×M\) 的圖

以左上角為起點、右下角為終點
其中有 \(R\) 個障礙物在上面
任何有障礙物的地方皆不得進入
請問到終點有多少種最短路徑？
請將答案模 \(10^9+7\) 後輸出
若根本沒有路能到終點，則輸出 "Path No Found."

 

\(2 \leq N、M \leq 2000\)

\(0 \leq R \leq 1000\)

Subtask.1 (5%)

保證圖是正方形，邊長不超過 10

欸隨便窮舉就有五分了誒，真的不考慮做一下嗎

void solve (){
  int N, M, R; cin >> N >> M >> R;
  switch (N){
    case 2: cout << "2\n"; break;
    case 3: cout << "6\n"; break;
    case 4: cout << "20\n"; break;
    case 5: cout << "70\n"; break;
    case 6: cout << "252\n"; break;
    case 7: cout << "924\n"; break;
    case 8: cout << "3432\n"; break;
    case 9: cout << "12870\n"; break;
    case 10: cout << "48620\n"; break;
  };
}
# PRESENTING CODE

部分分解答 (可得分數：5%)

  • 不會演算法也要會一點數學
  • 不會數學也要會一點 Google
  • 不會 Google 的話，你可以來一點 Teacher. Bonnie

Subtask.2 (10%)

圖形是矩形，邊長不超過 10

其實我本來這個 subtask 是亂做的

# PRESENTING CODE

部分分解答 (可得分數：15%)

  • 為了維持最短路徑，我們只能 往右走 或 往下走
  • 往右走 跟 往下走 的順序根本沒有差

數學解思維

  • 有 \(a\) 個往下跟 \(b\) 個往右，求排列數
\frac{p^{a+b}_{a+b}}{P^{a}_{a}\;P^{b}_{b}} \; = \; \frac{(a+b)!}{a! \; b!}
  • 但有個小問題... \(20! \; = \; 2432902008176640000\)
  • 爆 unsigned long long，理論上 你不會做
# PRESENTING CODE

部分分解答 (可得分數：15%)

DP 解思維

  • 我只有可能從上面或左邊過來

1

到此格的走法 =

到上面那格的走法 + 到左邊那格的走法

1

1

1

1

2

3

3

6

const int MAXN = 2017;
vector <vector <int>> graph(MAXN, vector <int>(MAXN, 0));

void solve (){
  int N, M, R; cin >> N >> M >> R;
  int ans = 0;
  for (int i = 1; i <= N; i++){
    for (int j = 1; j <= M; j++){
      if (i == 1 && j == 1) graph[i][j] = 1;
      else graph[i][j] = graph[i-1][j] + graph[i][j-1];
    }
  }
  ans = graph[N][M];
  cout << ans << '\n';
}

Subtask.3 (15%)

圖形是矩形，邊長不超過 2000

你以為我那個 mod 是寫好看的嗎

# PRESENTING CODE

部分分解答 (可得分數：30%)

  • 同餘定理（詳見運算思維的數論簡報）：

$$(a+b)\;\%\;m \; = \; (a\;\%\;m+b\;\%\;m)\;\%\;m$$

$$(a-b)\;\%\;m \; = \; (a\;\%\;m-b\;\%\;m)\;\%\;m$$

$$(a\,b)\;\%\;m \; = \; [(a\;\%\;m)\,(b\;\%\;m)]\;\%\;m$$

  • 非常好模板
ll Mod (ll a, int m = MOD){
  return (a+m) % m;
}

ll Plus (ll a, ll b, int m = MOD){
  return Mod(Mod(a) + Mod(b));
}

ll Minus (ll a, ll b, int m = MOD){
  return Mod(Mod(a) - Mod(b));
}

ll Mult (ll a, ll b, int m = MOD){
  return Mod(Mod(a) * Mod(b));
}
# PRESENTING CODE

部分分解答 (可得分數：30%)

數學解思維

\frac{p^{a+b}_{a+b}}{P^{a}_{a}\;P^{b}_{b}} \; = \; \frac{(a+b)!}{a! \; b!}
vector <int> factorial(2007, -1);
void solve (){
  int N, M, R; cin >> N >> M >> R;
  int tmp = 1;
  for (int i = 1; i <= N+M; i++){
    tmp =  Mult(tmp, i);
    factorial[i] = tmp;
  }
  cout << factorial[N+M] / factorial[N] / factorial[M] << '\n';
}

答案會是爛的。因為同餘定理 不支援除法

你可以套 模反元素 解決此問題，或乾脆換個做法吧

# PRESENTING CODE

部分分解答 (可得分數：30%)

DP 解思維

const int MOD = 1e9 + 7;
ll Mod (ll a, int m = MOD){
  return (a+m) % m;
}

ll Plus (ll a, ll b, int m = MOD){
  return Mod(Mod(a) + Mod(b));
}

const int MAXN = 2017;
vector <vector <int>> graph(MAXN, vector <int>(MAXN, 0));

void solve (){
  int N, M, R; cin >> N >> M >> R;
  int ans = 0;
  for (int i = 1; i <= N; i++){
    for (int j = 1; j <= M; j++){
      if (i == 1 && j == 1) graph[i][j] = 1;
      else graph[i][j] = Plus(graph[i-1][j], graph[i][j-1]);
    }
  }
  ans = graph[N][M];
  cout << ans << '\n';
}

Correct Answer

理論上做完障礙就可以一次過了

剩下的 subtask 是在你寫出 bug 的情況下才會卡到

但我教你們寫 bug 幹嘛

# PRESENTING CODE

AC Code（可得分數：100 %）

  • 初始化：除了起點設為 1，其他所有格都默認為 0
  • 障礙物：做個 0 以外的標記，這裡把它改成 -1
void solve (){
  for (int i = 0; i < MAXN; i++)
    for (int j = 0; j < MAXN; j++)
        graph[i][j] = 0;

  int N, M, R; cin >> N >> M >> R;
  for (int i = 0; i < R; i++){
    int x, y; cin >> x >> y;
    graph[x][y] = -1;
  }
  
  //...
}
  • 如果在 DP 時遇到障礙，改 -1 為 0 並跳過
# PRESENTING CODE

AC Code（可得分數：100 %）

#include <bits/stdc++.h>
#define icisc ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
#define ll long long int
using namespace std;

const int MOD = 1e9 + 7;
ll Mod (ll a, int m = MOD){
  return (a+m) % m;
}

ll Plus (ll a, ll b, int m = MOD){
  return Mod(Mod(a) + Mod(b));
}

const int MAXN = 2017;
vector <vector <int>> graph(MAXN, vector <int>(MAXN, 0));

void solve (){
  for (int i = 0; i < MAXN; i++)
    for (int j = 0; j < MAXN; j++)
        graph[i][j] = 0;

  int N, M, R; cin >> N >> M >> R;
  for (int i = 0; i < R; i++){
    int x, y; cin >> x >> y;
    graph[x][y] = -1;
  }
  for (int i = 1; i <= N; i++){
    for (int j = 1; j <= M; j++){
      if (graph[i][j] == -1){
        graph[i][j] = 0;
        continue;
      }else if (i == 1 && j == 1){
        graph[i][j] = 1;
      }else{
        graph[i][j] = Plus(graph[i-1][j], graph[i][j-1]);
        // printf("At [%d, %d], = %d + %d\n", i, j, graph[i-1][j], graph[i][j-1]);
      }
    }
  }
  if (graph[N][M] == 0) cout << "Path No Found.\n";
  else cout << graph[N][M] << '\n';
}

int main (){
  icisc
  solve();
}
  • 若 ans = 0，別忘了輸出 Path No Found

超級常見的 bug

其實之前教你們的講師就講錯

雖然他偷偷修正回來，而且沒有發公告，壞透了

# PRESENTING CODE

bug 解 (可得分數：30%)

  • 初始化的時候...
 int N, M, R; cin >> N >> M >> R;
 for (int i = 1; i <= N; i++) graph[i][1] = 1;
 for (int i = 1; i <= M; i++) graph[1][i] = 1;
  • 有發現連範測都過不了嗎？我故意給這筆的

1

X

0

1

1

X

1

0

1

1

X

1

1

1

X

1

1

2

正解

bug 解