DP 優化
今天會講的內容
- 矩陣快速冪優化
- 單調隊列優化
其他來不及講的內容
- 狀態壓縮
- 斜率優化
- 四邊形優化
- Alien 優化
- ...
什麼是 DP 優化?
DP 優化指的是透過一些特定資料結構用法或想法,去減少求解的時間 / 空間複雜度!
例如:
矩陣快速冪優化可將單次查詢時間從 \(O(n) \)壓到 \(O(\log n)\)
但是優化也要看場合,不能亂砸!
例如:
進行 \(q\) 次詢問,矩陣快速冪會是 \(O(q \log n)\) ,一般轉移仍是 \(O(n)\)
DP 求解三部曲
定義狀態
推出轉移式
依照轉移式
決定優化方式
1
2
3
矩陣快速冪優化
啥是矩陣快速冪?


const int mod = 1e9 + 7;
struct Mat {
// n*n 方陣
ll A[MAXN][MAXN];
int n;
Mat(int _n){
n=_n;
memset(A, 0, sizeof(A));
}
};
Mat operator *(const Mat &m1, const Mat &m2) {
assert(m1.n == m2.n);
int n = m1.n;
Mat ret(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
ret.A[i][j] += m1.A[i][k] * m2.A[k][j];
ret.A[i][j] %= mod;
}
}
}
return ret;
}
先來看個題目
用 \(1 \times 2\) 的骨牌填滿 \(2 \times n\) 的格子,共有幾種排法?
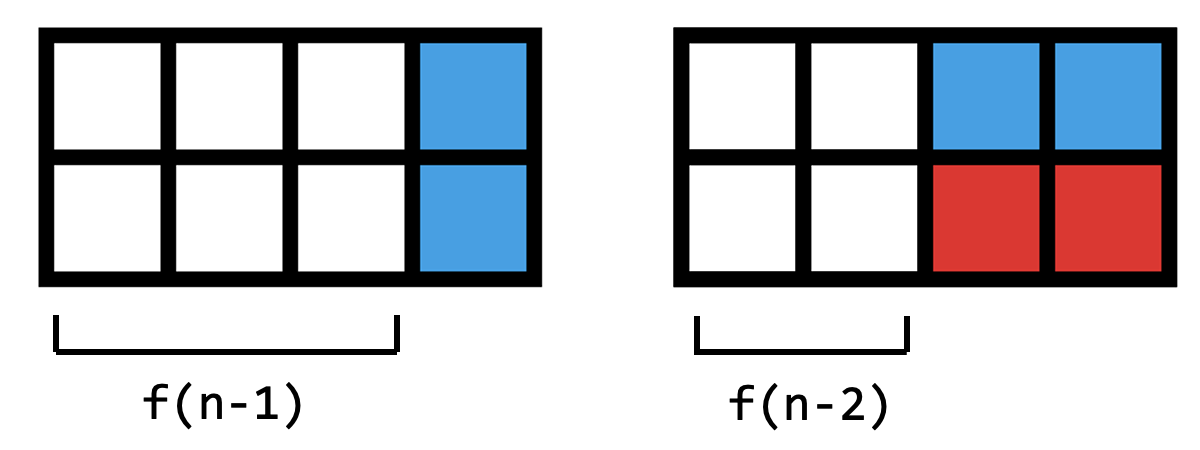
1. 定義狀態:定義 \(f(n)\) 為格子寬度 \(n\) 時的排法
2. 導出轉移式:定義 \(f(n)\) 為格子寬度 \(n\) 時的排法
\( f(n) = f(n-1) + f(n-2)\)
其實就是費氏數列

\( f(n) = f(n-1) + f(n-2)\)
\( f(n) = f(n-1) + f(n-2)\)
\( f(n-1) = f(n-1) + 0\)

\( f(n) = f(n-1) + f(n-2)\)
\( f(n-1) = f(n-1) + 0\)
用矩陣來紀錄 DP 狀態!
所以我們現在可以將 DP 狀態和轉移式以矩陣表示了
然後勒?
一樣慢慢用乘法來算 \({\begin{bmatrix}1 & 1\\1 & 0\end{bmatrix}}^{n-1}\) 嗎?
複雜度 \(O(n)\)
有沒有快一點的算法可以算出一個矩陣的 \(n\) 次方?
快速冪!➜ \( O(\log n)\)
矩陣有結合律!
所以也可以快速冪!
const int mod = 1e9 + 7;
struct Mat {
// n*n 方陣
ll A[MAXN][MAXN];
int n;
Mat(int _n){
n=_n;
memset(A, 0, sizeof(A));
}
};
Mat operator *(const Mat &m1, const Mat &m2) {
assert(m1.n == m2.n);
int n = m1.n;
Mat ret(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
ret.A[i][j] += m1.A[i][k] * m2.A[k][j];
ret.A[i][j] %= mod;
}
}
}
return ret;
}
Mat pow (Mat a, int n) {
Mat ans(a.n);
for (int i = 0; i < a.n; ++i) {
ans.A[i][i]=1;
}
for (int i=1;i<=n;i<<=1) {
if (n&i) ans = ans * a;
a = a * a;
}
return ans;
}
矩陣快速冪優化適用範圍
矩陣快速冪優化適用範圍
如果一個 DP 轉移式
有辦法表達成
其中\(M_i\)為狀態矩陣,\(A\)為轉移(?)矩陣
則
事實上和數學上的轉移矩陣概念很像似,但定義不一樣,純屬亂用名次
可使用矩陣快速冪優化
矩陣快速冪優化適用範圍
更具體來說,
當dp式為線性遞迴式,且 O(n) 太慢的時候
就可以用矩陣快速冪優化!
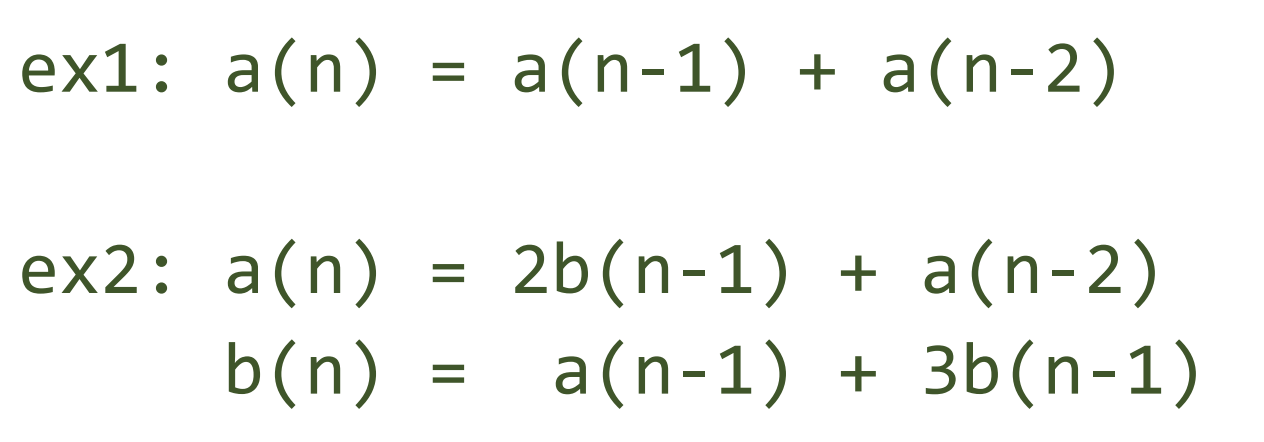
矩陣快速冪優化適用範圍
可是,要如何建立那個轉移用的矩陣呢?
方法1: 憑感覺亂湊
現在來講方法2
- 將遞迴式寫好
\(a(n) = 2*b(n-1) + b(n) + a(n-3) \)
\(b(n) = 2a(n-2) + b(n-1)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) = 2*b(n-1) + b(n) + a(n-3) \)
\(b(n) = 2a(n-2) + b(n-1)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) = 2*b(n-1) + 2a(n-2) + b(n-1) + a(n-3) \)
\(b(n) = 2a(n-2) + b(n-1)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) = 2*b(n-1) + 2a(n-2) + b(n-1) + a(n-3) \)
\(b(n) = 2a(n-2) + b(n-1)\)
\(a(n-1) =\)
\(a(n-2) = \)
\(a(n-1)\)
\(a(n-2)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) = 2*b(n-1) + 2a(n-2) + b(n-1) + a(n-3) \)
\(b(n) = 2a(n-2) + b(n-1)\)
\(a(n-1) =\)
\(a(n-2) = \)
\(a(n-1)\)
\(a(n-2)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) =0*a(n-1) + 2*a(n-2) + 1*a(n-3) + 3*b(n-1) \)
\(b(n) = 0*a(n-1) + 2*a(n-2) + 0*a(n-3) + 1*b(n-1) \)
\(a(n-1) =1*a(n-1) + 0*a(n-2) + 0*a(n-3) + 0*b(n-1) \)
\(a(n-2)\)
\(a(n-2) =0*a(n-1) + 1*a(n-2) + 0*a(n-3) + 0*b(n-1) \)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) =0*a(n-1) + 2*a(n-2) + 1*a(n-3) + 3*b(n-1) \)
\(b(n) = 0*a(n-1) + 2*a(n-2) + 0*a(n-3) + 1*b(n-1) \)
\(a(n-1) =1*a(n-1) + 0*a(n-2) + 0*a(n-3) + 0*b(n-1) \)
\(a(n-2)\)
\(a(n-2) =0*a(n-1) + 1*a(n-2) + 0*a(n-3) + 0*b(n-1) \)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(1\)
\(2\)
\(2\)
\(3\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) =0*a(n-1) + 2*a(n-2) + 1*a(n-3) + 3*b(n-1) \)
\(b(n) = 0*a(n-1) + 2*a(n-2) + 0*a(n-3) + 1*b(n-1) \)
\(a(n-1) =1*a(n-1) + 0*a(n-2) + 0*a(n-3) + 0*b(n-1) \)
\(a(n-2)\)
\(a(n-2) =0*a(n-1) + 1*a(n-2) + 0*a(n-3) + 0*b(n-1) \)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(1\)
\(2\)
\(2\)
\(3\)
\(a(n-1)\)
\(a(n-2)\)
\(a(n-3)\)
\(b(n-1)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) =\)
\(b(n) = \)
\(a(n-1) =\)
\(a(n-2) =\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(1\)
\(2\)
\(2\)
\(3\)
\(a(n-1)\)
\(a(n-2)\)
\(a(n-3)\)
\(b(n-1)\)
如何建立那個轉移用的矩陣
2. 整理遞迴式
\(a(n) \,=\)
\(b(n) \, = \)
\(a(n-1) \,=\)
\(a(n-2)\, =\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(1\)
\(2\)
\(2\)
\(3\)
\(a(n-1)\)
\(a(n-2)\)
\(a(n-3)\)
\(b(n-1)\)
如何建立那個轉移用的矩陣
3. 整理成次方式
矩陣快速冪練習
將下列題目整理成次方式
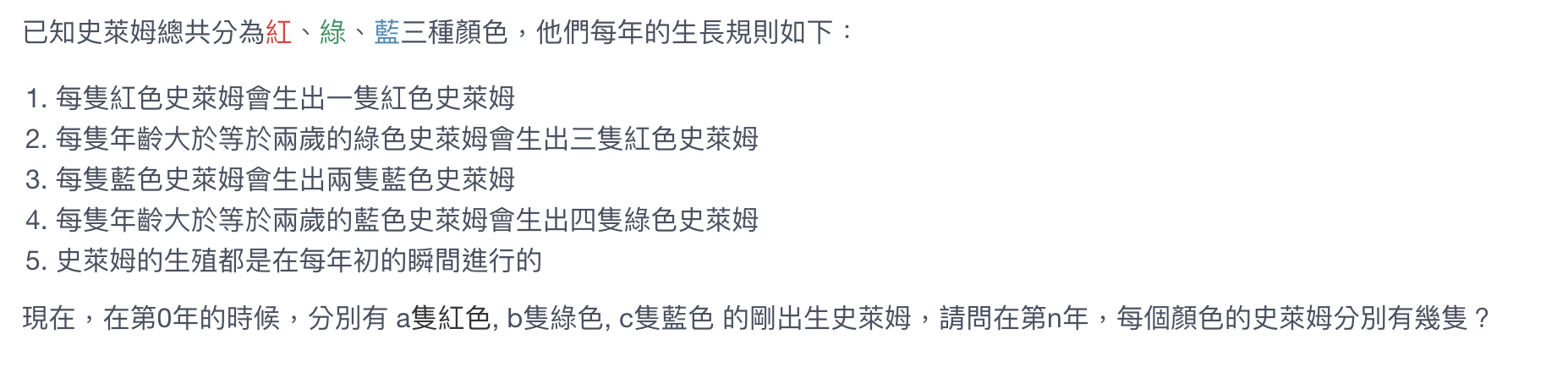
將下列題目整理成次方式

回家練習
- TIOJ 2053 (easy)
- TIOJ 1331 (怪怪的,要用unsigned int 自動取 mod,題目有點出爛)
- iscoj 4460 (hard)
More 題目
來看看剛剛那題的 code
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define endl '\n'
#define AI(x) begin(x),end(x)
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int mod = 1e9 + 7;
struct Mat {
// n*n 方陣
vector<vector<ll>> A;
int n;
Mat(int _n){
n=_n;
for (int i = 0; i < n; ++i) {
A.pb(vector<ll>(n));
}
}
};
Mat operator *(const Mat &m1, const Mat &m2) {
assert(m1.n == m2.n);
int n = m1.n;
Mat ret(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
ret.A[i][j] += m1.A[i][k] * m2.A[k][j];
ret.A[i][j] %= mod;
}
}
}
return ret;
}
Mat pow (Mat a, int n) {
Mat ans(a.n);
for (int i = 0; i < a.n; ++i) {
ans.A[i][i]=1;
} // 斜角化
for (int i=1;i<=n;i<<=1) {
if (n&i) ans = ans * a;
a = a * a;
}
return ans;
}
signed main(){_
int n, a, b, c;
cin >> n >> a >> b >> c;
Mat K(5);
K.A = {{2, 0, 0, 3, 0},
{0, 1, 0, 0, 4},
{0, 0, 3, 0, 0},
{0, 1, 0, 0, 0},
{0, 0, 1, 0, 0}};
Mat I(5);
I.A = {{a, 0, 0, 0, 0},
{b, 0, 0, 0, 0},
{c, 0, 0, 0, 0},
{0, 0, 0, 0, 0},
{0, 0, 0, 0, 0}};
Mat R = pow(K, n) * I; // R = (K^n) * I
cout << R.A[0][0] << " ";
cout << R.A[1][0] << " ";
cout << R.A[2][0] << "\n";
return 0;
}
單調隊列優化
一樣先來看個題目
給定一整數陣列,求取出數字的總合最大,且滿足兩數距離不能大於K
1. 定義狀態:dp[i]: 從前i個數中取數,且有取到arr[i]的最大總合
2. 轉移式:dp[i] = arr[i] + max (dp[i-k], dp[i-k+1], ... dp[i-1])
3. 答案:max( dp[1], dp[2], dp[3], ... , dp[n] )
暴力複雜度:\(O(n^2)\)
如何優化?
要取區間 max
砸線段樹!
複雜度:\(O(n \log n)\)
可是線段樹好難寫喔
有沒有更好更快的方法?
轉移式:\(dp[i] = arr[i] + \max (dp[i-k], dp[i-k+1], ... dp[i-1])\)
如何優化?
方法三
我們可以發覺,取 max 的左界是遞增的
一個東西如果被淘汰了,就永遠用不到!
用 heap (priority_queue) 維護最大值!
- push:記錄該點的值和位置
- top :如果取到的值已經「過期」了則直接丟掉,直到 top 不是過期的
複雜度:\(O(n \log n)\)
轉移式:\(dp[i] = arr[i] + \max (dp[i-k], dp[i-k+1], ... dp[i-1])\)
如何優化?
轉移式:\(dp[i] = arr[i] + \max (dp[i-k], dp[i-k+1], ... dp[i-1])\)
方法4
我們可以觀察到一件事情
假設存在 i, j 使得 i < j 且 dp[i] < dp[j]
當我們在取 max 時,就絕對不會取到 dp[i]
不過
假設存在 i, j 使得 i > j 且 dp[i] < dp[j]
則 dp[i] 就仍可能用得到(當 j 被淘汰時)
如何優化?
繼續看下去,回到一開始暴力的想法
你可以發覺取 max 的範圍會像是一個 sliding window
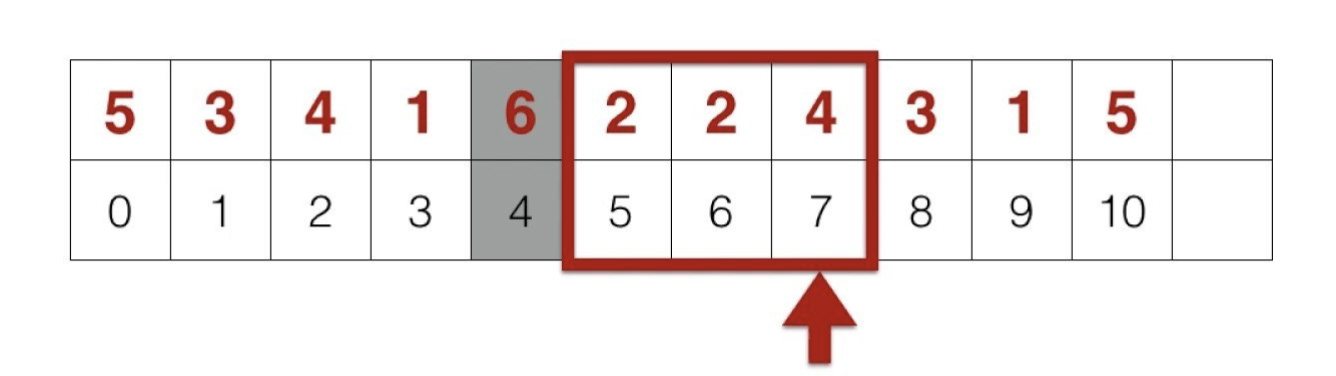
會不斷往右移
方法4
轉移式:\(dp[i] = arr[i] + \max (dp[i-k], dp[i-k+1], ... dp[i-1])\)
作法:
方法4
轉移式:\(dp[i] = arr[i] + \max (dp[i-k], dp[i-k+1], ... dp[i-1])\)
用一個 deque 稱為 mono假設今天更新到 dp[i]-
while 左邊的東西 index < (i-k)將左邊東西 pop 掉-
index 在範圍內,mono 最右邊的東西就是範圍內最大值
算出 dp[i]-
while 右邊的東西 dp 值小於 dp[i]把他從右邊 pop 掉
將 {dp[i], i} 放入mono右邊
作法:
方法4
轉移式:\(dp[i] = arr[i] + \max (dp[i-k], dp[i-k+1], ... dp[i-1])\)
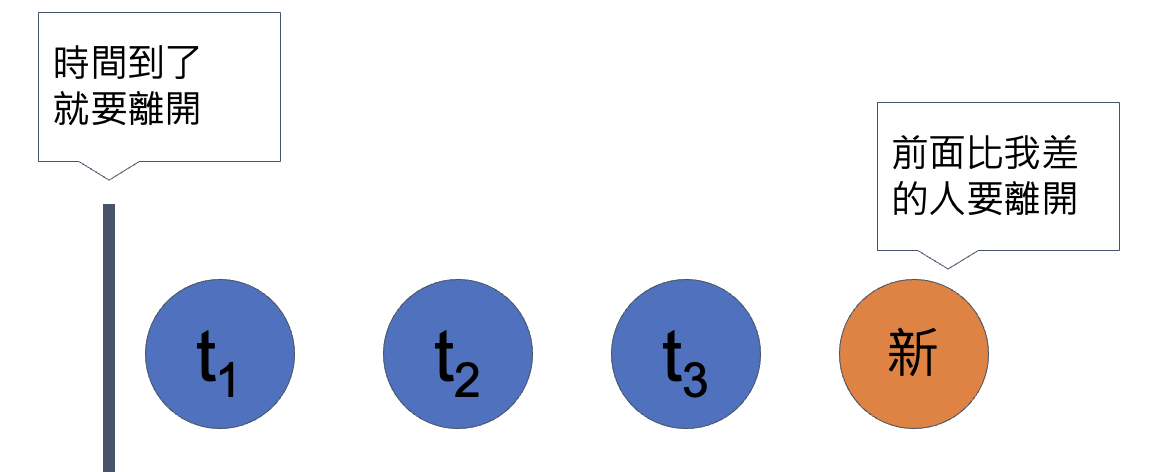
容器裡面的東西會具有單調性
這個做法我們稱之為單調隊列!
source: 資訊之芽
單調隊列優化適用範圍
轉移式長相:
\(dp[i] = \max (dp[L_i] \sim dp [i] ) \) + ...
其中,\(L_i\) 會遞增
就可以用單調隊列優化
單調隊列練習
無聊單調數列
其實就是單調隊列中最核心的那部分程式碼

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
signed main(){_
int n;
cin >> n;
vector<int> a(n);
vector<int> b(n);
vector<int> c(n);
for (auto &i : a) cin >> i;
for (auto &i : b) cin >> i;
deque <pair<int, int>> mono; // {i, a[i]}
for (int i = 0; i < n; ++i) {
while (!mono.empty() && mono.back().second < a[i]) {
mono.pop_back();
}
mono.push_back({i, a[i]});
while (!mono.empty() && mono.front().first < b[i]) {
mono.pop_front();
}
c[i] = mono.front().second;
}
for (int i = 0; i < n; ++i) {
cout << c[i] << " ";
}
cout << endl;
return 0;
}
再一題
給定一個長度為n的序列,找一個長度不超過m的連續子序列,使得選擇的數的總和最大
dp[i] = sum[i] - min(sum[i-j]), 0 ≤ j ≤ m
= sum[i] - min(sum[k]), i - m ≤ k ≤ i
可以對 sum[k] 用單調隊列!