Joint Optimization of an Autoencoder for Clustering and Embedding

 

Ahcène Boubekki

Michael Kampffmeyer

Ulf Brefeld

Robert Jenssen

 

UiT The Arctic

University of Norway

Leuphana University

Questions

  • Can we approx. k-means with an NN?

  • How to jointly learn an embedding?

Clustering Module

step by step

     Step by step: Assumptions

Assumptions of k-means

Hard clustering

Null co-variances

Equally likely clusters

Relaxations

Soft assignments

\gamma_{ik} = p(z_i = k \:|\: x_i)

Isotropic co-variances

\forall k, \: \Sigma_k = \frac{1}{2}I_d

Dirichlet prior on

{ \tilde{ \gamma } }_k = \frac{1}{N} \sum_i \gamma_{ik}

Isotropic GMM

     Step by step: Gradient Descent

Isotropic GMM with Dirchlet prior

\mathcal{Q}( \bm \Gamma,\bm \Phi,\bm \mu) = \sum_{ik} \gamma_{ik} \log \phi_k - \sum_{ik} \gamma_{ik} ||x_i - \mu_k||^2
+ \sum_k(\alpha_k-1) \log \tilde{ \gamma}_k

Gradient Descent fails :(

Algorithmical trick

After an M-step:

\phi_k = \frac{1}{n} \sum_i \gamma_{ik} = \tilde{ \gamma_k }

Simplification due to the prior

     Step by step: Where is the AE?

Current Objective function:

\mathcal{Q}( \bm \Gamma,\bm \mu) = - \sum_{ik} \gamma_{ik} ||x_i - \mu_k||^2 + \sum_k(\alpha_k-1) \log \tilde{ \gamma}_k

Computational trick

AE ⇒ reconstruction

+ \sum_i || \bar x_i ||^2 - \sum_i || \bar x_i ||^2 %%+ \sum_i \Big( || \sum_k \gamma_{ik} \mu_k ||^2 - || \sum_k \gamma_{ik} \mu_k ||^2 \Big)
\mathcal{Q}( \bm \Gamma,\bm \mu) = - \sum_{ik} \gamma_{ik} ||x_i - \mu_k||^2 + \sum_k(\alpha_k-1) \log \tilde{ \gamma}_k
= - \sum_{i} ||x_i - \bar x_i||^2 + \ldots
\vdots
= - \sum_i||x_i - \bar x_i||^2 + \ldots
\text{with} \quad \bar x_i = \sum_k \gamma_{ik} \mu_k
= - \sum_{i} ||x_i - \bar x_i||^2 + \sum_{ik} \gamma_{ik}(1 - \gamma_{ik}) ||\mu_k||^2
- \sum_{k \neq l} \big( \sum_i \gamma_{ik} \gamma_{il} \big) \big( \mu_k^\top \mu_l \big) - \sum_k (1-\alpha_k ) \log \tilde\gamma_{k}

     Clustering Module

Loss Function

\mathrm{Softmax}
x_i
\bar x_i
\gamma_i
\mu
\mathcal{L} = \sum_{i} ||x_i - \bar x_i||^2
- \sum_{ik} \gamma_{ik}(1 - \gamma_{ik}) ||\mu_k||^2
+ \sum_k (1-\alpha_k ) \log \tilde\gamma_{k}
+ \sum_{k \neq l} \big( \sum_i \gamma_{ik} \gamma_{il} \big) \big( \mu_k^\top \mu_l \big) \\

Reconstruction

Sparsity + Reg.

Sparsity + Merging

Dir. Prior

\gamma_i = \mathcal{F}(x_i ; \bm \eta)
\bar x_i = \mathcal{G}(\gamma_i; \bm\mu) = \gamma_i^\top \bm \mu
\gamma_{i} = \big\langle p(z_i=k| x_i) \big\rangle_K
\gamma_i \in \mathbb{S}^K

Network

\eta
\gamma_i = \sigma( x_i^\top \bm \eta )

     Clustering Module: Evaluation

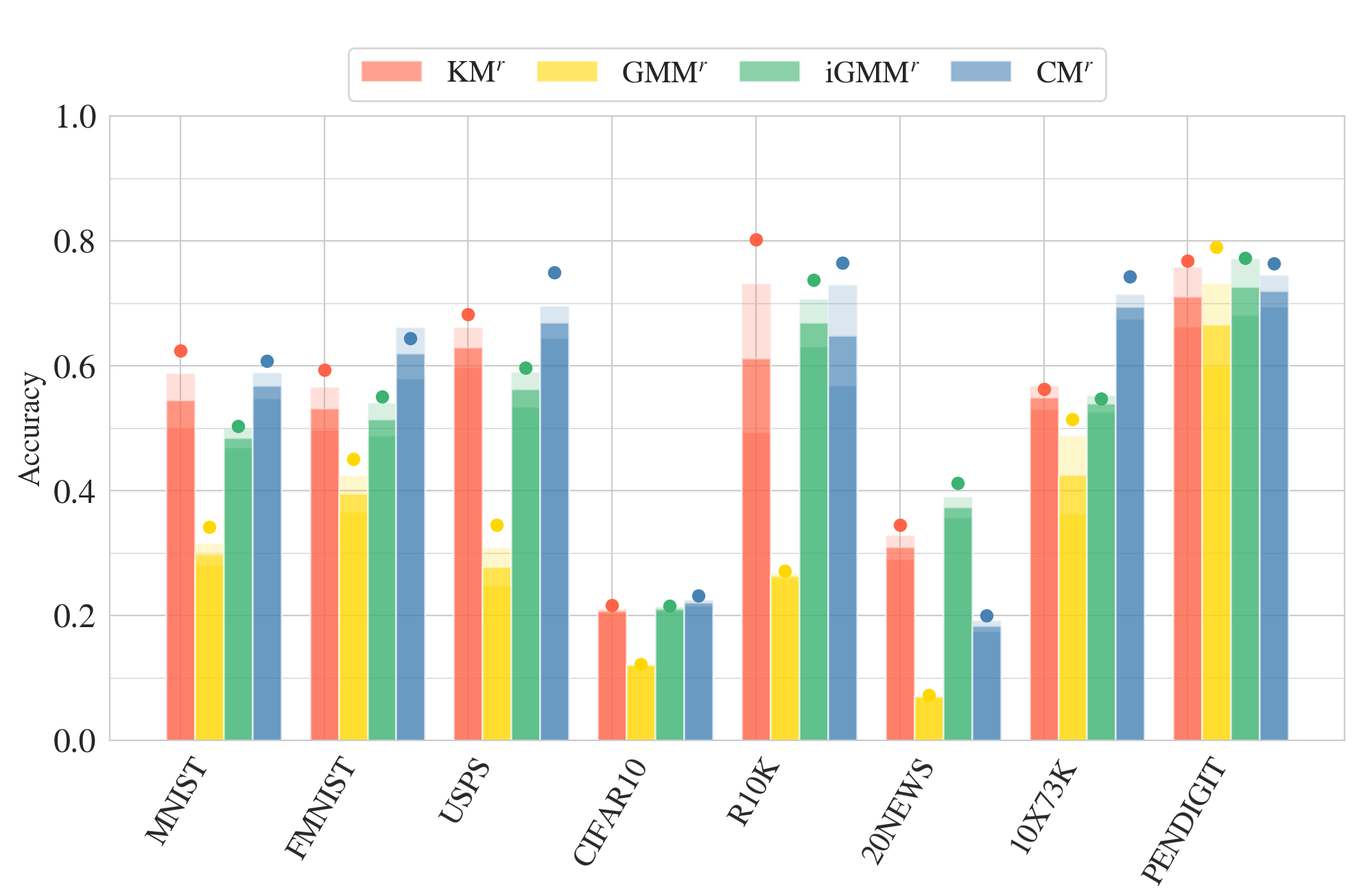
Baselines:





 

Best run

Average
St.Dev

k-means

GMM

iGMM

Accuracy

     Clustering Module: Summary

YES

Limitations

Isotropy assumption

Linear partitions only

Tied co-variances

Spherical co-variances

we can cluster à la k-means using a NN

What is the solution?

Kernels!

Feature maps

Clustering Module
and Feature Maps

     AE-CM: Introduction

CM

x
\bar x
z
\psi

Invertible feature maps to avoid collapsing

Maps are learned using a neural network

AE-CM

     AE-CM

Loss Function

Lagrange

\mathcal{L} = \beta \sum_{i} ||x_i - \bar x_i||^2 + \sum_{i} ||z_i - \bar z_i||^2
+ \sum_k (1-\alpha_k ) \log \tilde\gamma_{k}
- \sum_{ik} \gamma_{ik}(1 - \gamma_{ik}) ||\mu_k||^2 + \sum_{k \neq l} \big( \sum_i \gamma_{ik} \gamma_{il} \big) \big( \mu_k^\top \mu_l \big) \\
\mathcal{L} = \beta \sum_{i} ||x_i - \bar x_i||^2 + \sum_{i} ||z_i - \bar z_i||^2
+ \sum_k (1-\alpha_k ) \log \tilde\gamma_{k}
- \sum_{ik} \gamma_{ik}(1 - \gamma_{ik}) \hspace{2.5cm} \text{with } \mu_k^\top \mu_l = \delta_{kl}
\mathcal{L} = \beta \sum_{i} ||x_i - \bar x_i||^2 + \sum_{i} ||z_i - \bar z_i||^2
+ \sum_k (1-\alpha_k ) \log \tilde\gamma_{k}
- \sum_{ik} \gamma_{ik}(1 - \gamma_{ik}) + \lambda ||\bm\mu^T \bm\mu - I_K||_1 \hspace{2.5cm}

does not

meet expectations

CM

x
\bar x
z

Orthonormal

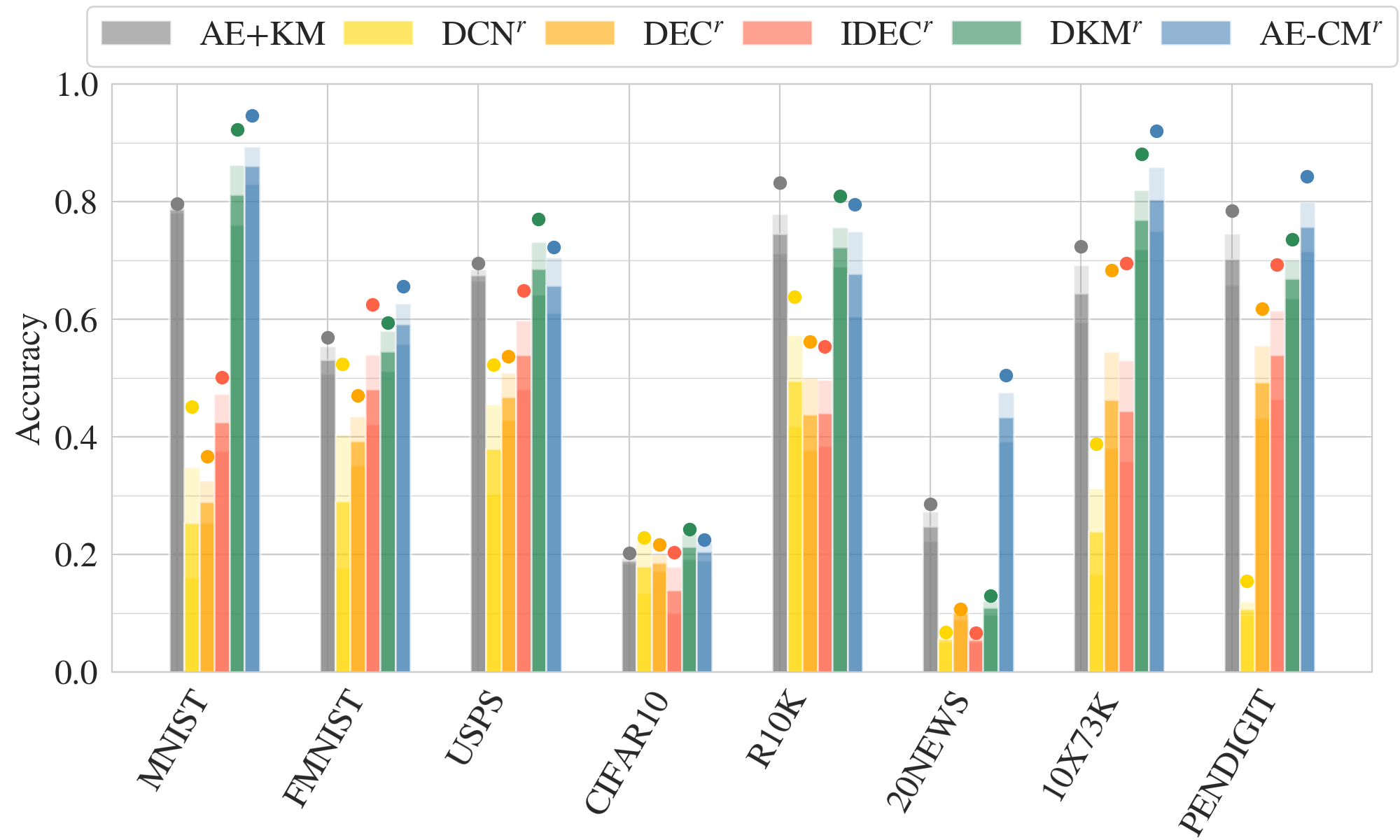
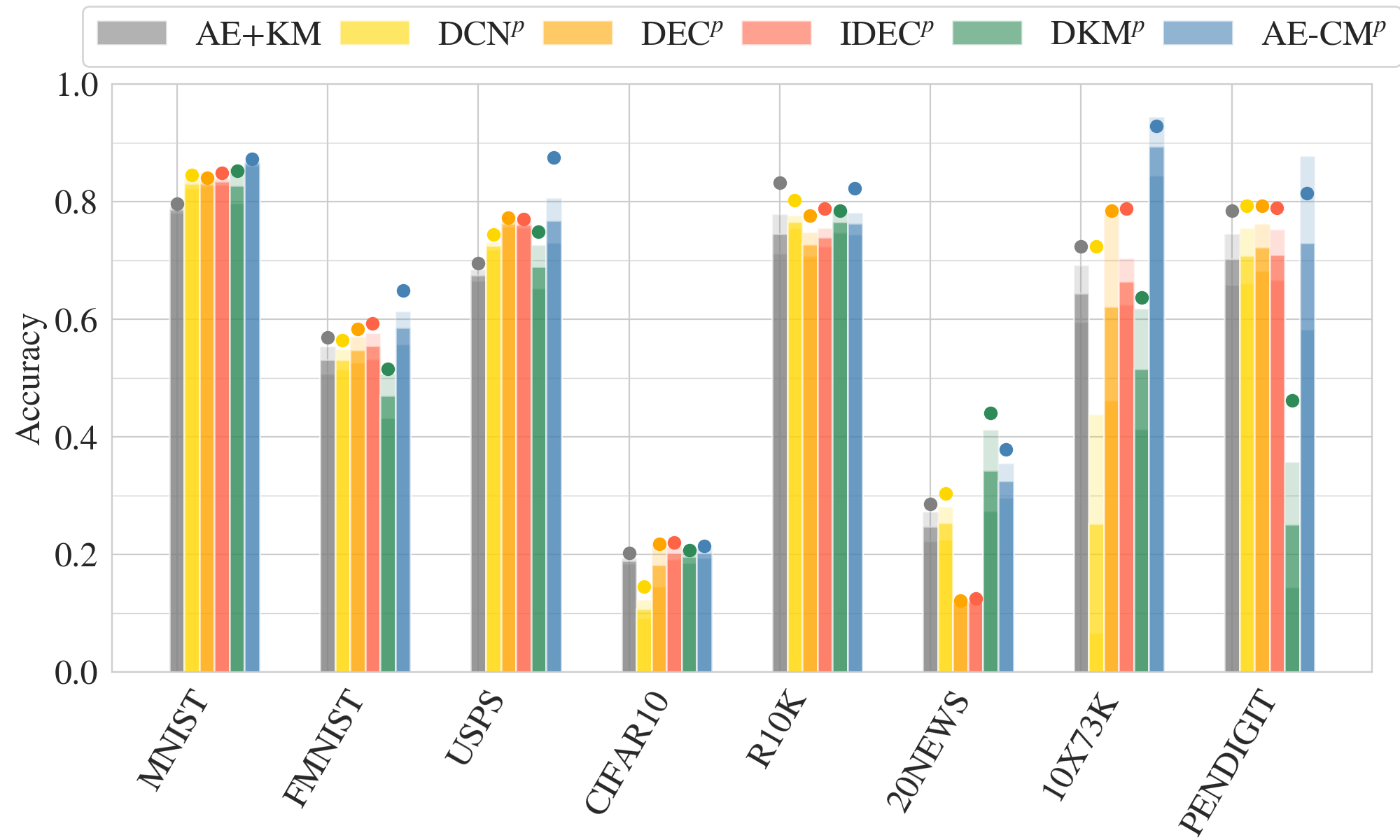
     AE-CM: Baselines

AE+KM:

DCN:

Initialization:

  • Pre-train DAE
  • Centroids and hard assignments from k-means in feature space
     

Alternate:

  • Minimize NN for reconstruction DAE and k-means
  • Update hard assignments
  • Update centroids

 

End-to-end autoencoder + k-means

DEC:

Initialization:

  • Pre-train DAE
  • Centroids and soft assignments from k-means in feature space
  • Discard decoder

Alternate:

  • t-SNE like loss on DAE
  • Update centroids

IDEC:

Same but keep the decoder

DKM:

centroids in ad-hoc matrix

Loss = reconstruction DAE + c-means-like term

Annealing of Softmax temperature

AE+KM:

(2017) DCN:

(2016) DEC:

(2017) IDEC:

(2020) DKM:

Check paper for GAN and VAE baselines

Fully connected layers

     AE-CM: Evaluation with random initialization

     AE-CM: Evaluation initalized with AE+KM

     AE-CM: Toy example

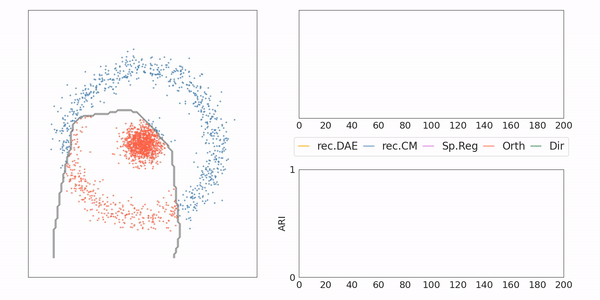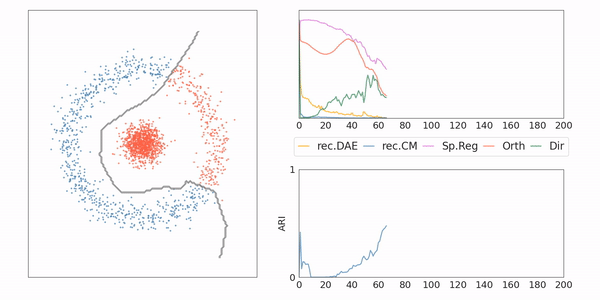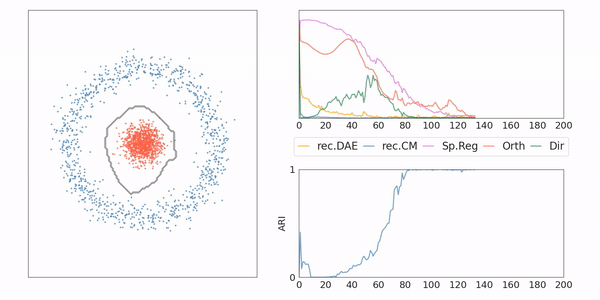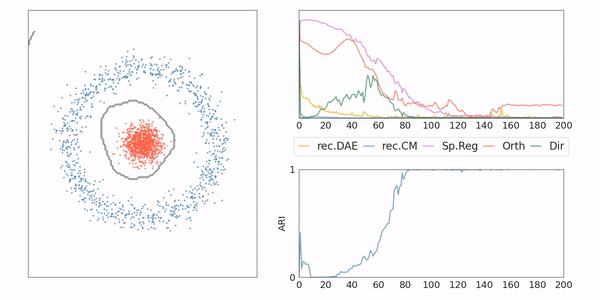
     AE-CM: Generative Model

Conclusion

     Conclusion

YES

What is next?

Can we approx. k-means with a NN?

Can we jointly learn an embedding?

YES

Improve stability by acting on assignments.

Softmax annealing, Gumbel-Softmax, VAE

Try more complex architectures.

More applications.

Normalize the loss

Joint Optimization of an Autoencoder for Clustering and Embedding

 

Ahcène Boubekki

Michael Kampffmeyer

Ulf Brefeld

Robert Jenssen

 

UiT The Arctic

University of Norway

Leuphana University

Ekstra

     Clustering Module: Implementation

\mathrm{Softmax}
x_i
\bar x_i
\gamma_i
\mu
\:\mu\:
\eta

Initialization

Random

k-means++

Finalization

Averaging epoch

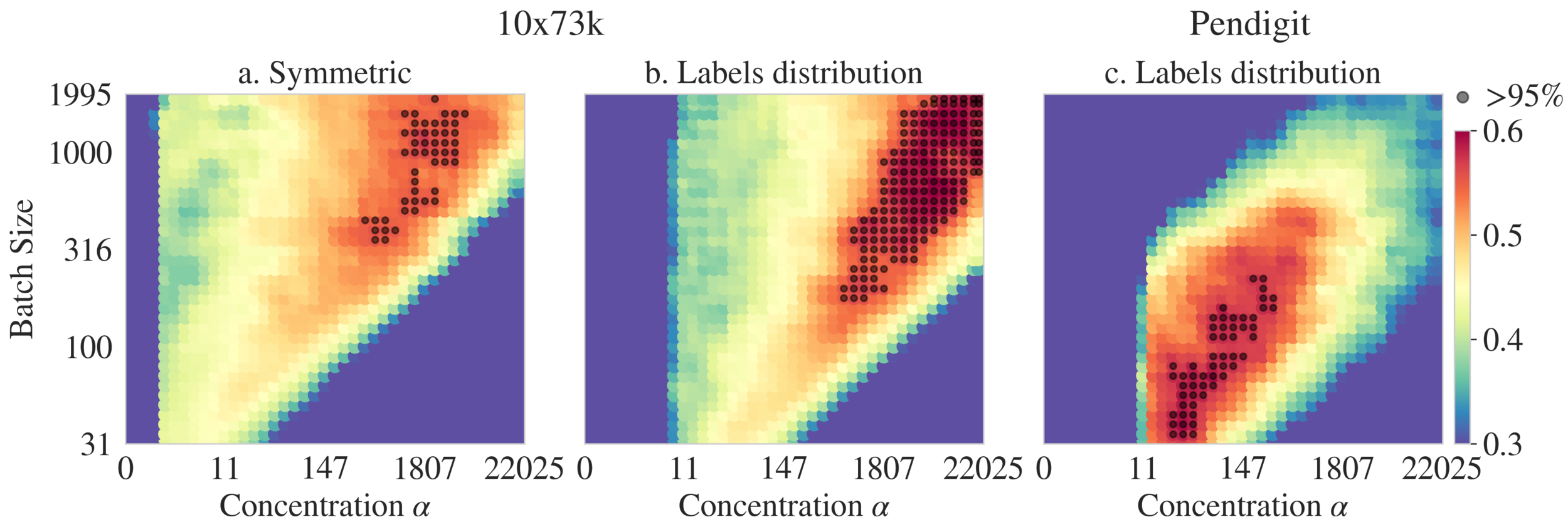
     Clustering Module: Hyperparameters

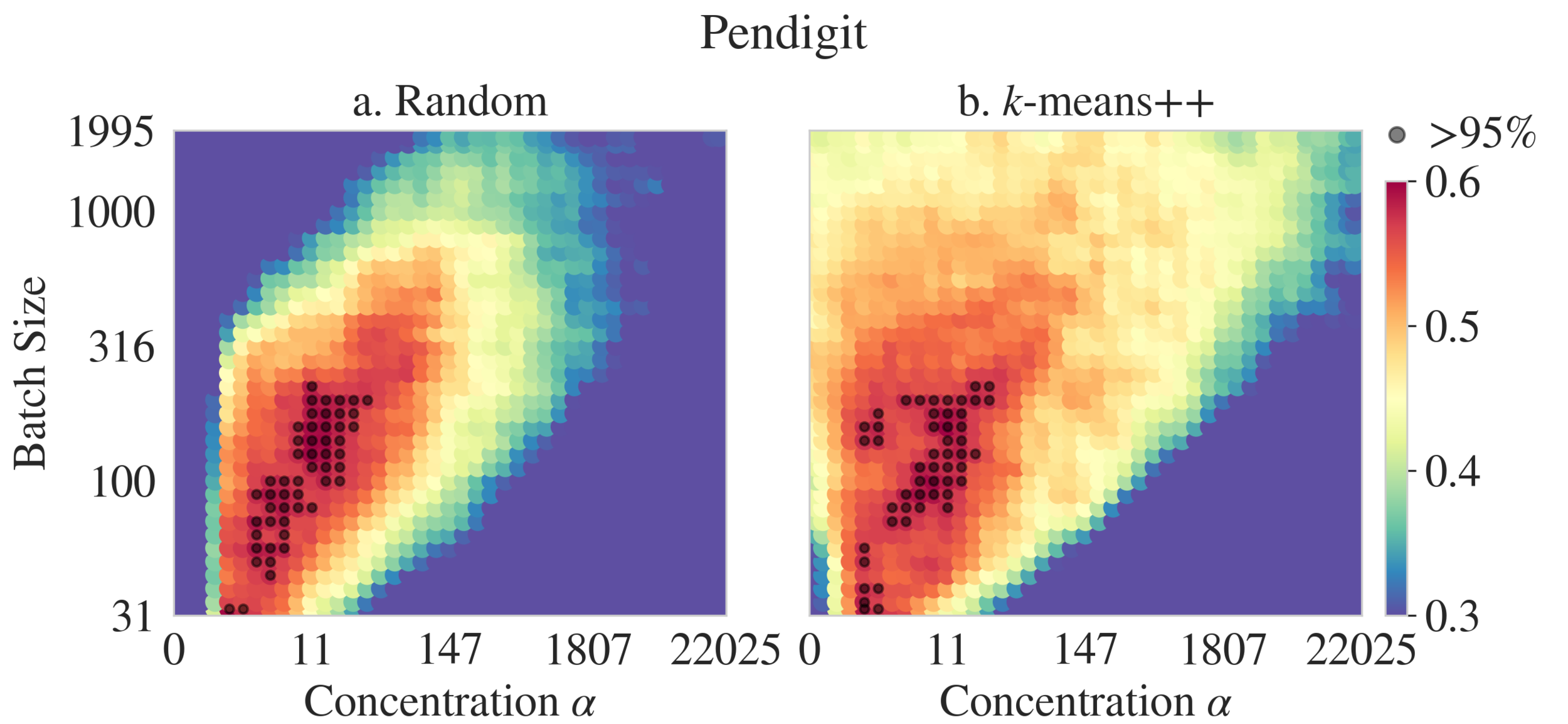
     CM: Prior

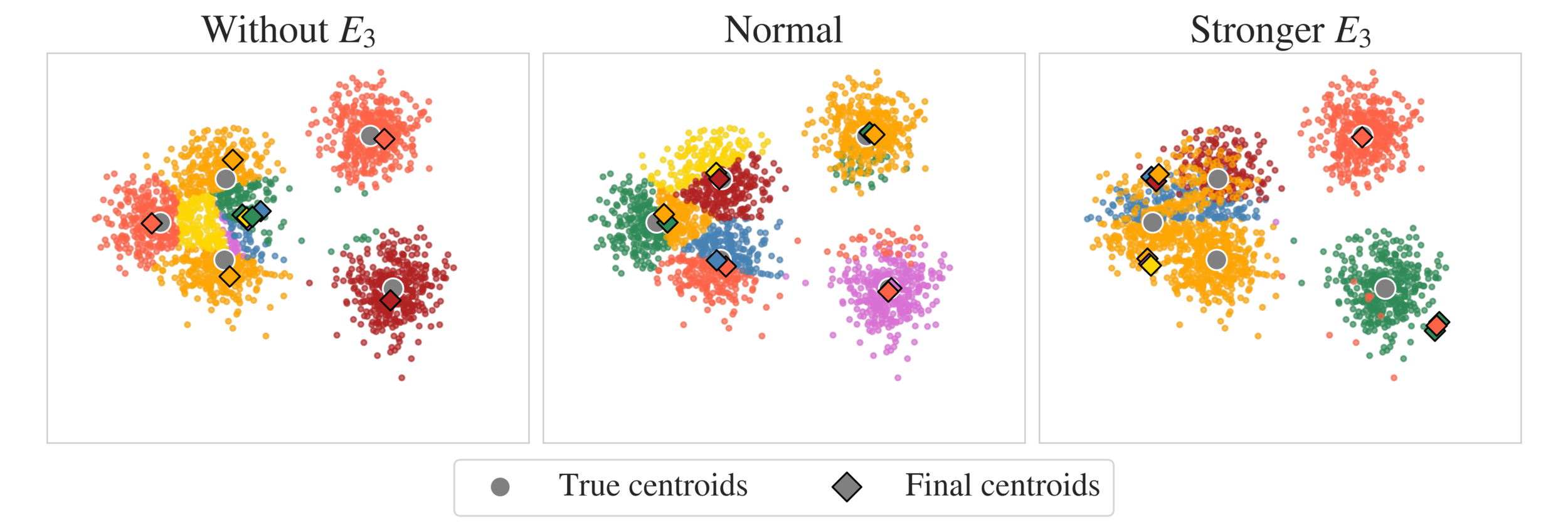
     CM: E3

     AE-CM: Beta vs Lambda

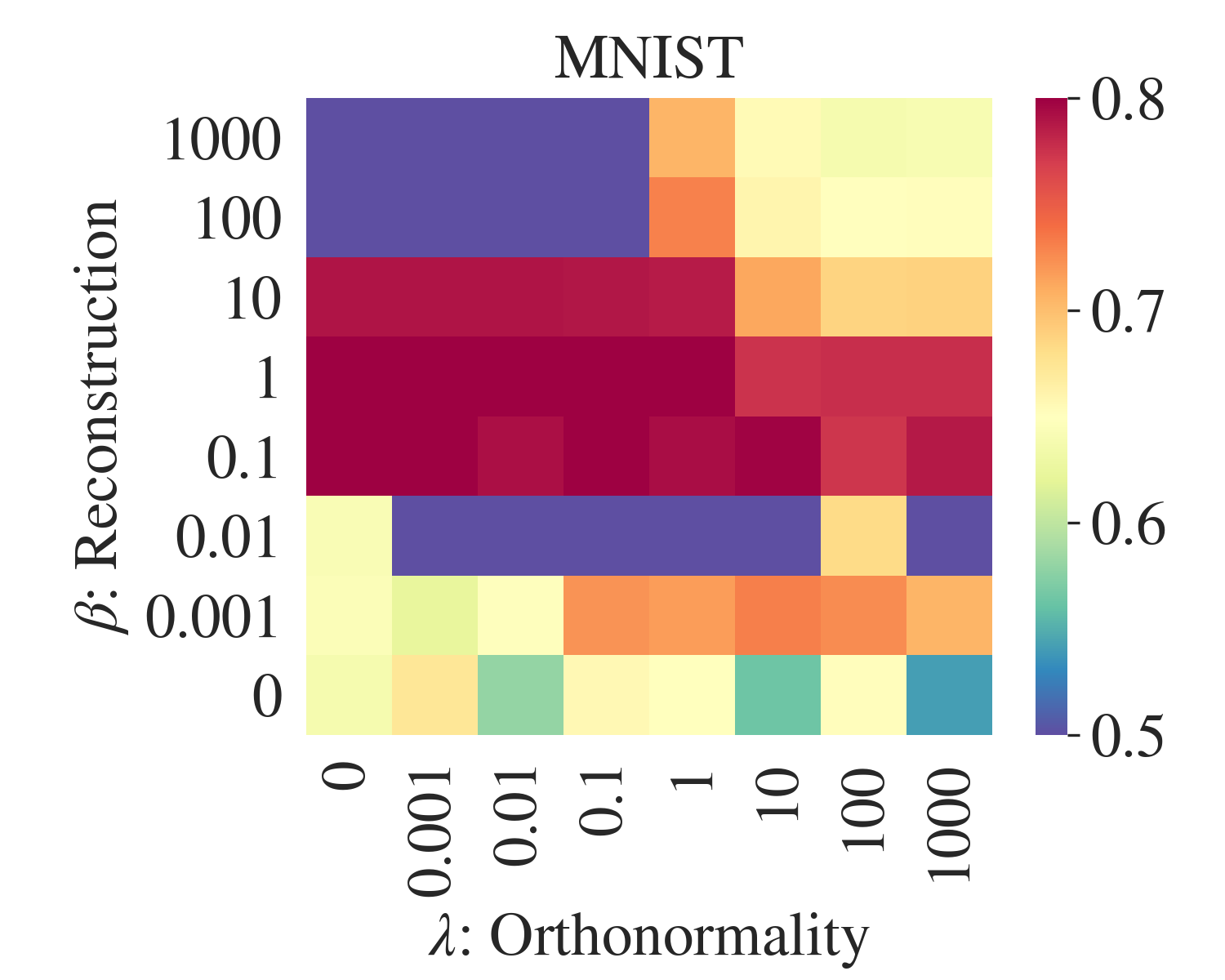
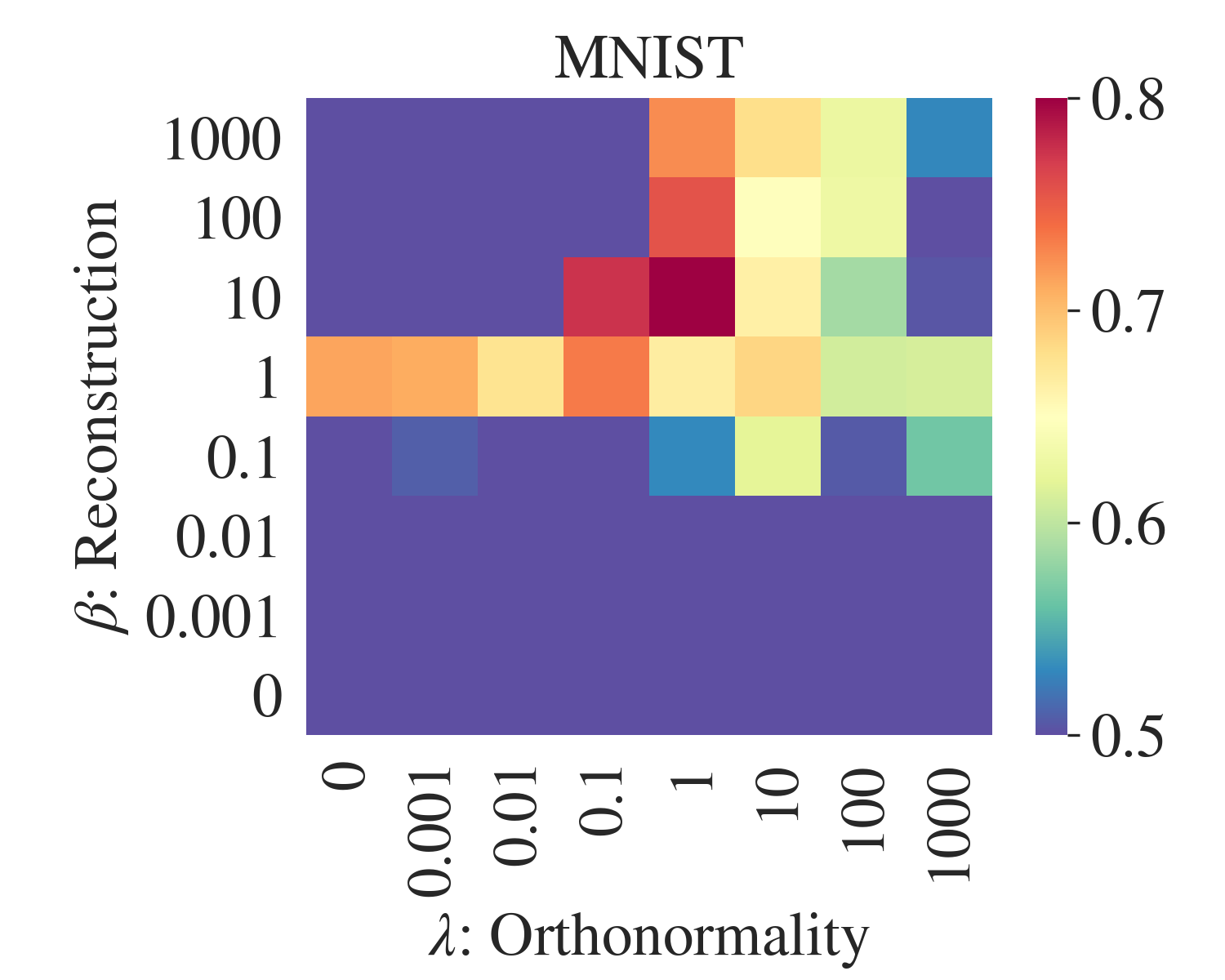
AE-CM+pre

AE-CM+rand

Motivation

To use NN to learn an embedding suitable for k-means/GMM

suitable

Linearly separable