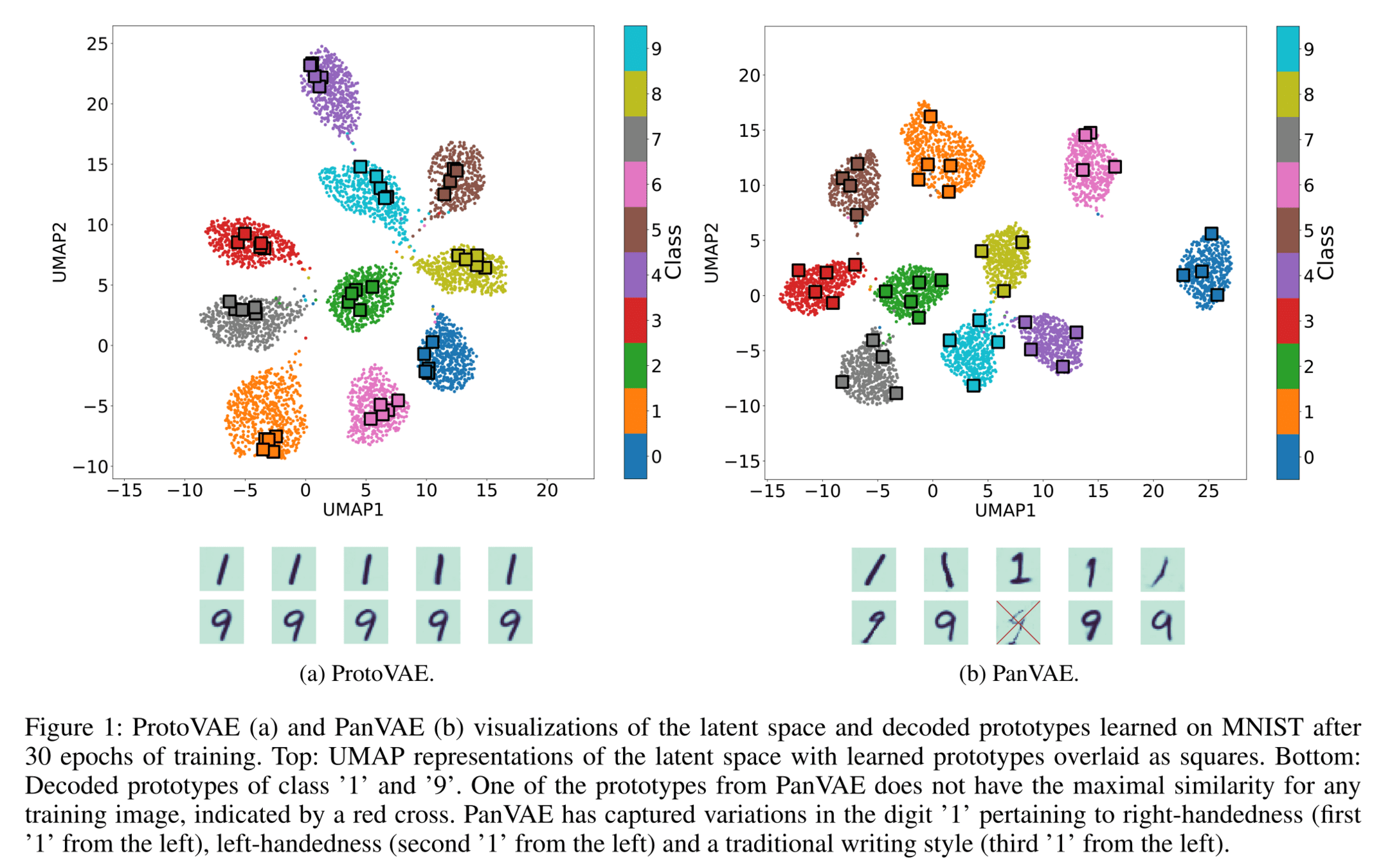
Pantypes: Diverse Representatives for Self-Explainable Models

 

Rune Kjærsgaard

Ahcène Boubekki

Line Clemmensen

 

DTU, Denmark

PTB, Germany

DTU, Denmark

Motivation

Improve prototypes' diversity

     Motivation

What is Diversity?

Geometric diversity

In the embedding

Combinatorial diversity

In terms of attributes

High Geometric

Low Combinatorial

Low Geometric

High Combinatorial

High Geometric

High Combinatorial

Celis, L. Elisa, et al. "How to be fair and diverse?." arXiv:1610.07183 (2016)

Pantypes

     Pantypes

Pantypes builds upon ProtoVAE

Gautam, Srishti, et al. "Protovae: A trustworthy self-explainable prototypical variational model." Neurips (2022)

⊕ Robust

⊕ Reconstruct prototypes

⊖ Slow training

⊖ Sensitive hyper-tuning

     Pantypes

ProtoVAE loss function:

\mathcal{L}_{\mathrm{ProtoVAE}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \mathcal{L}_{\mathrm{orth}}
\mathcal{L}_{\mathrm{ProtoVAE}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \sum_{k} || \mathbf{\Phi}_k^T \mathbf{\Phi}_k - \mathbf{I}_M||_F^2

Explicit constraints on rank and norm.

Let's make these constraints implicit!

Orthonormal prototypes

Pantypes

     Pantypes

Pantypes loss function:

\mathcal{L}_{\mathrm{Pantypes}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \frac{1}{K} \sum_{k} \frac{1}{|\mathbf{G}_k|^\frac{1}{2}}
\text{with} \: \mathbf{G}_k = \mathbf{\Phi}^T_k \mathbf{\Phi}_k

Maximize the volume

of the prototypical Gram matrix.

⇝ Maximize norm and rank of      .

\mathbf{\Phi}_k

IF USED!

Regularized by the VAE loss

Maximize the volume

of the prototypical Gram matrix.

⇒ Maximize norm and rank of      .

\mathbf{G}_k

"Unused" prototypes diverge out-of-distribution

         maximizes the norm and rank of the prototypes

\mathcal{L}_\mathrm{vol}

          regularizes the norm of "used" prototypes

\mathcal{L}_\mathrm{VAE}
\mathcal{L}_{\mathrm{Pantypes}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \mathcal{L}_{\mathrm{vol}}

     Pantypes

Norm constraint

too strong

Missing

OOD prototype

Evaluation

Geometric Diversity

     Evaluation: Geometric Diversity

Davies-Bouldin Index

\operatorname{DB} = \frac{1}{K}\sum_k \max_{l \neq k} \frac{s_k+s_l}{d_{kl}}

The better the lower which indicates dense and well separated clusters

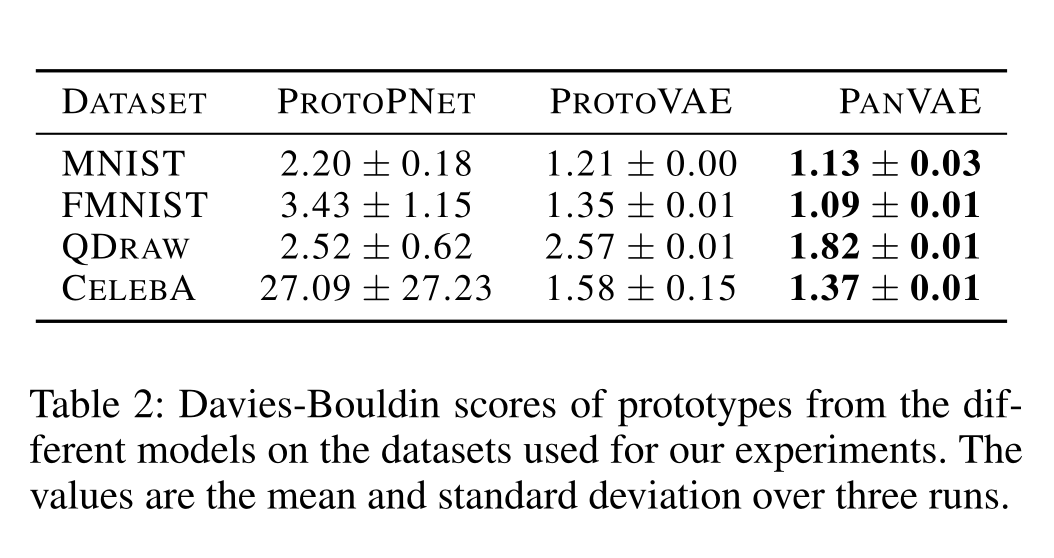
The better the lower which indicates dense and well separated clusters

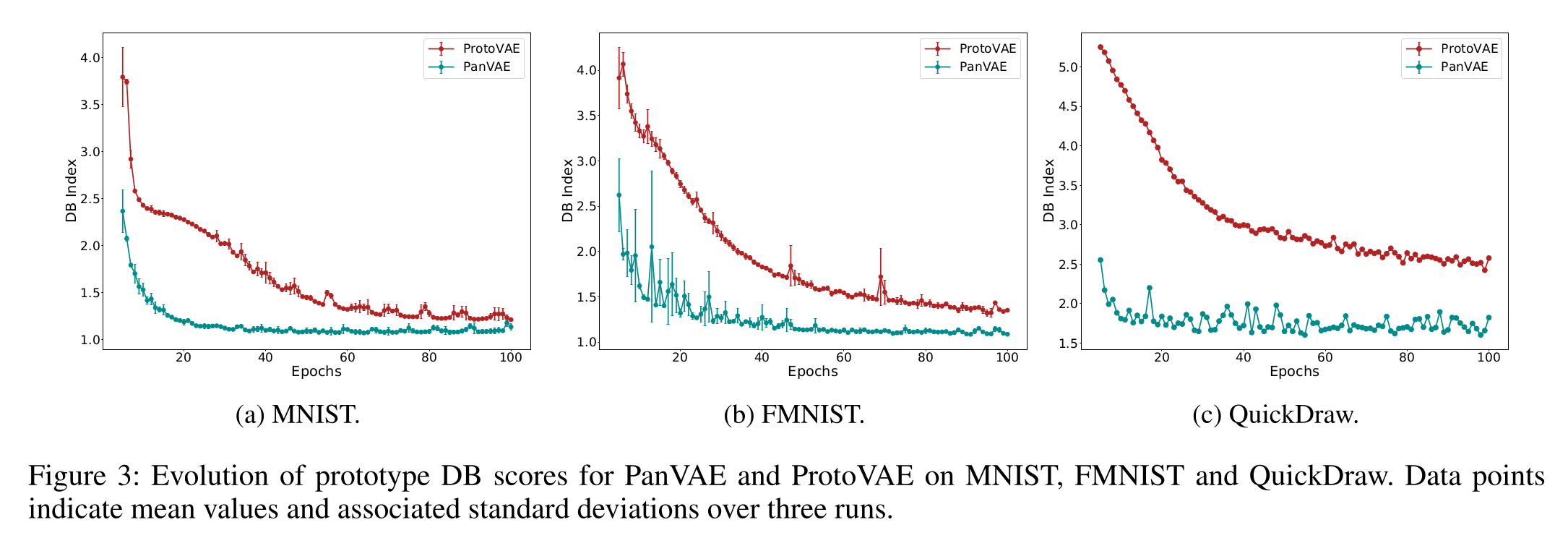
Pantypes

converge faster

     Evaluation: Geometric Diversity

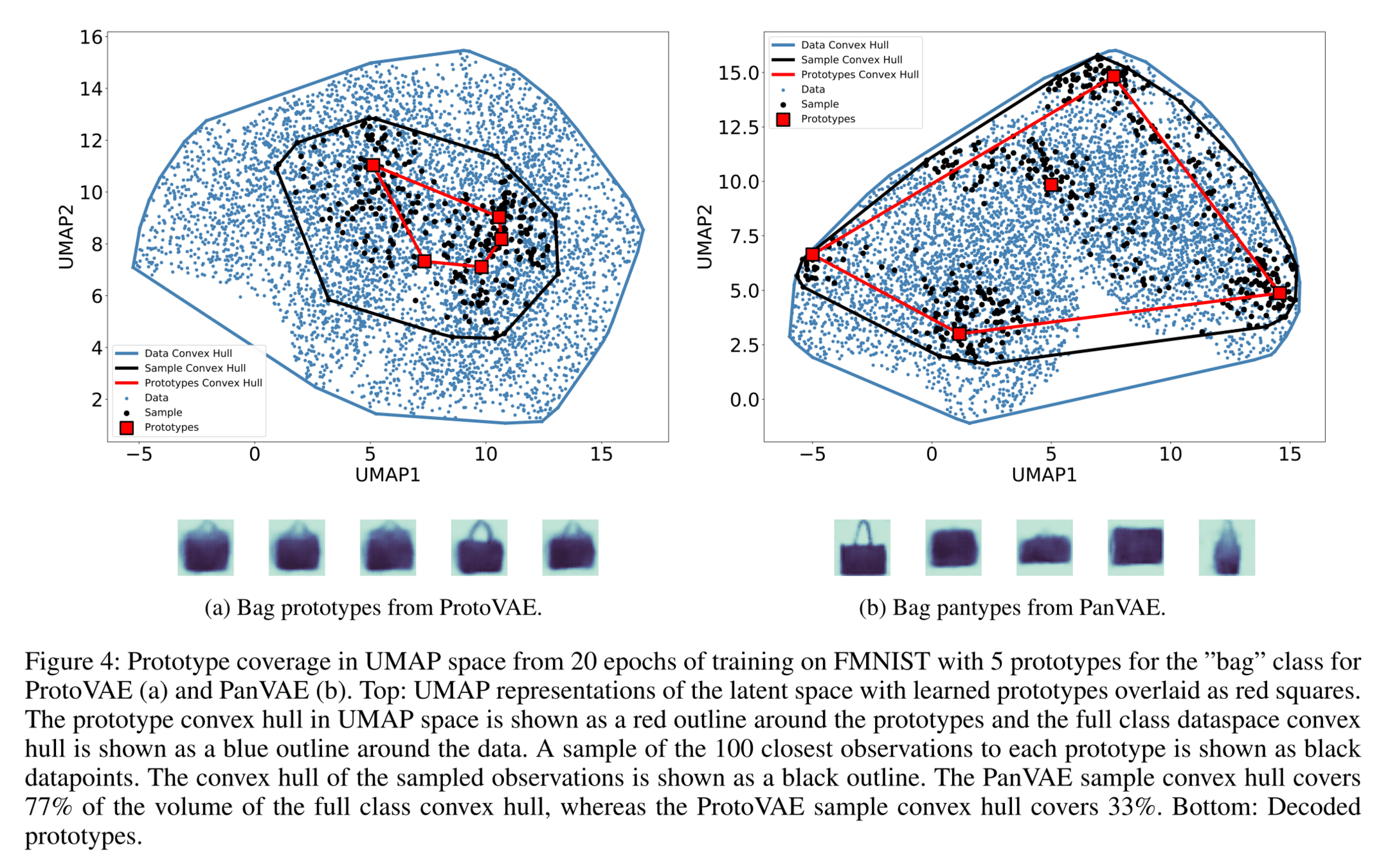
⏺ Data of class "bags"

⏹ Prototypes/Pantypes

⏺ 100 most similar points to each prototypes

━  Class' convex hull

━  Prototypes' convex hull

━  Subset's convex hull

\frac{\operatorname{Volume}(\hspace{2.5cm})}{\operatorname{Volume}(\hspace{2.5cm})}

Class' convex hull

Subset's convex hull

\text{Pantypes}:77\%
\text{ProtoVAE}:33\%

Evaluation

Combinatorial Diversity

     Evaluation: Combinatorial Diversity

Visual inspection:

UTKFace Large Scale Face Dataset https://susanqq.github.io/UTKFace/

     Evaluation: Combinatorial Diversity

Diversity Index

\begin{split} \operatorname{DI} & = H\left( \begin{array}{c} \text{probability an attribute} \\ \text{is captured by a prototype} \end{array} \right) \\ & = \sum_{a\in \operatorname{\tiny Attributes}} -p_a \log(p_a) \end{split}

A high entropy equates to a more diverse (fair) representation, which is not particularly biased towards any demographic group.

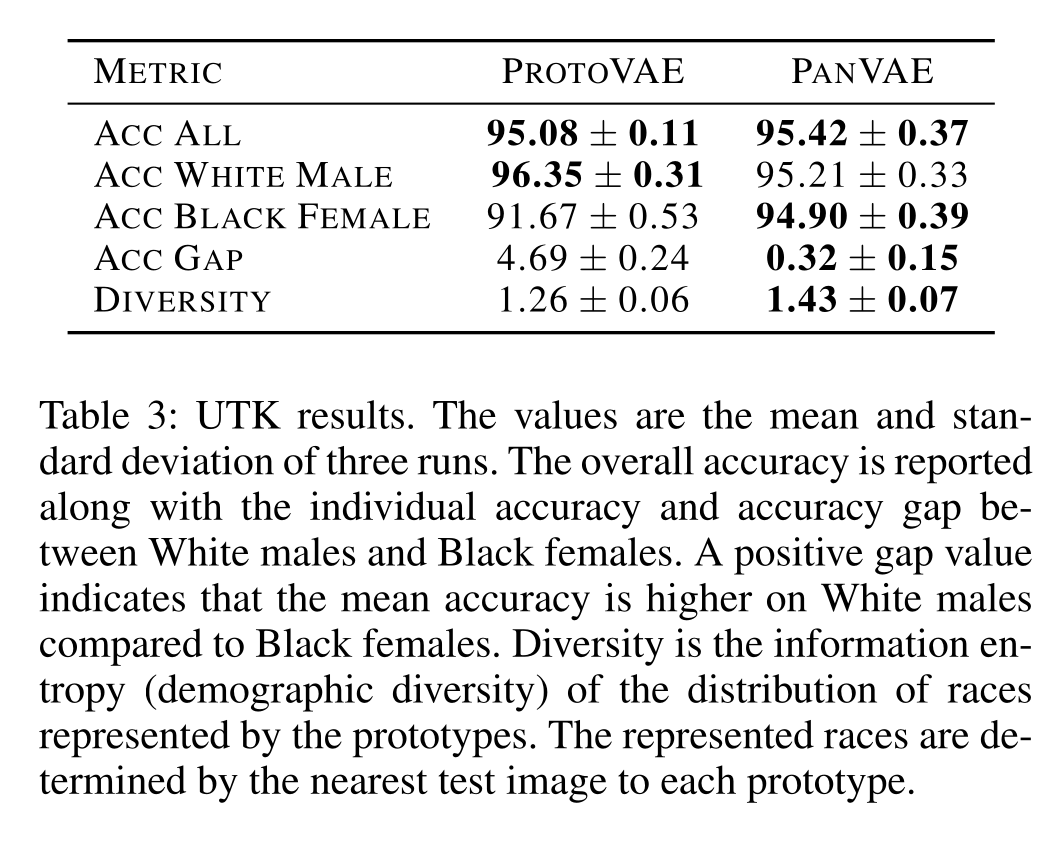
Higher

Diversity Index

Smaller

accuracy gap

\operatorname{Attributes} = \{ \mathrm{White}, \mathrm{Black}, \mathrm{Asian}, \mathrm{Indian}, \mathrm{Others} \} \times \{\mathrm{Female}, \mathrm{Male}\}.

UTKFace Large Scale Face Dataset https://susanqq.github.io/UTKFace/

Summary

     Summary

  • build upon a robust backbone.
  • maximize the volume of the prototypical Gram matrix.
  • enforce implicitly a constraint on rank and norm.
  • select automatically the prototypes.
  • Smaller Davies-Bouldin index that converges faster.
  • Smaller accuracy gap between White Male and Black Female.
  • Larger diversity index.

⇒ Better geometric and combinatorial diversity.

Pantypes

Evaluation

Pantypes: Diverse Representatives for Self-Explainable Models

 

Rune Kjærsgaard

Ahcène Boubekki

Line Clemmensen

 

DTU, Denmark

PTB, Germany

DTU, Denmark