Mining User Trajectories

in Electronic Textbooks

 

Ahcène Boubekki

Shailee Jain

Ulf Brefeld

 

Leuphana, Lüneburg

University of Texas at Austin

Leuphana, Lüneburg

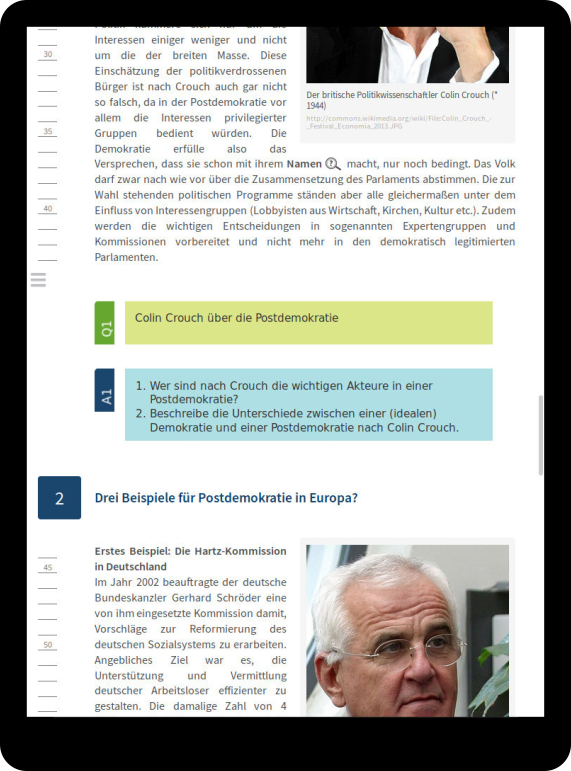
     mBook

Multimedia history textbook used in German schools in Belgium.

Since 2013 : 6 chapters

                       725 pages

                       478 galleries

                       3 000 users

                       37 000 sessions

                       780 000 clicks

                       75 tracked events

The Project:

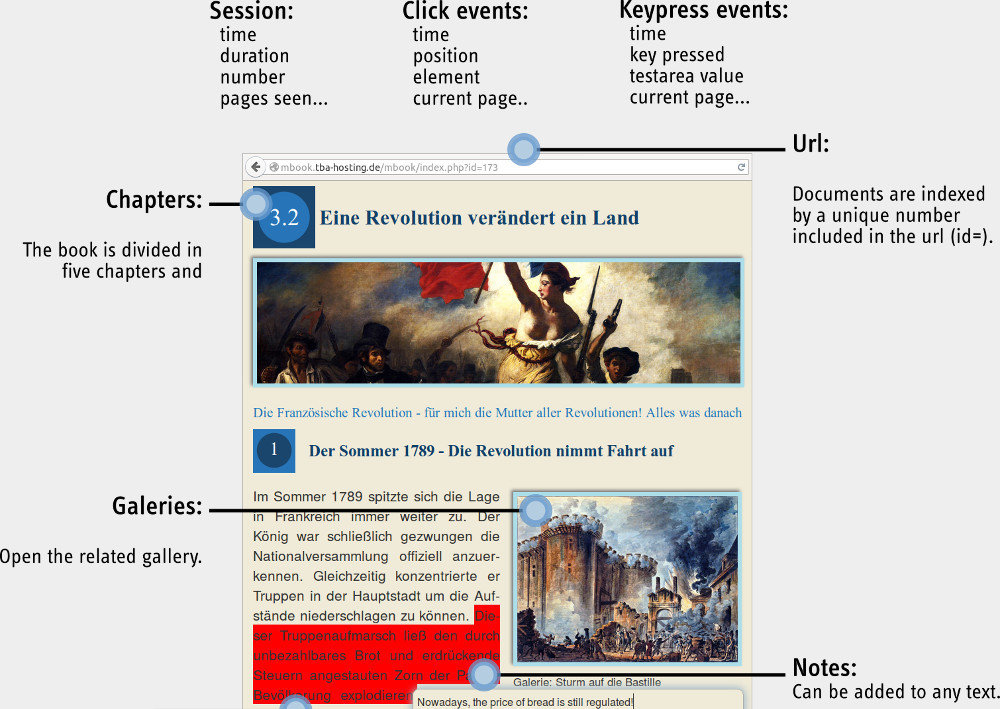
Research questions

Do all the pupils use the textbook the same way?

Is their behavior influenced by their ability in history or IT skills?

Can we predict the pupils ability in history or IT skills from their behavior?

How does the teacher influence these behaviors?

No

Local approach

Markov Chains

     Markov Chains

Cluster 1

Cluster 2

Cluster 3

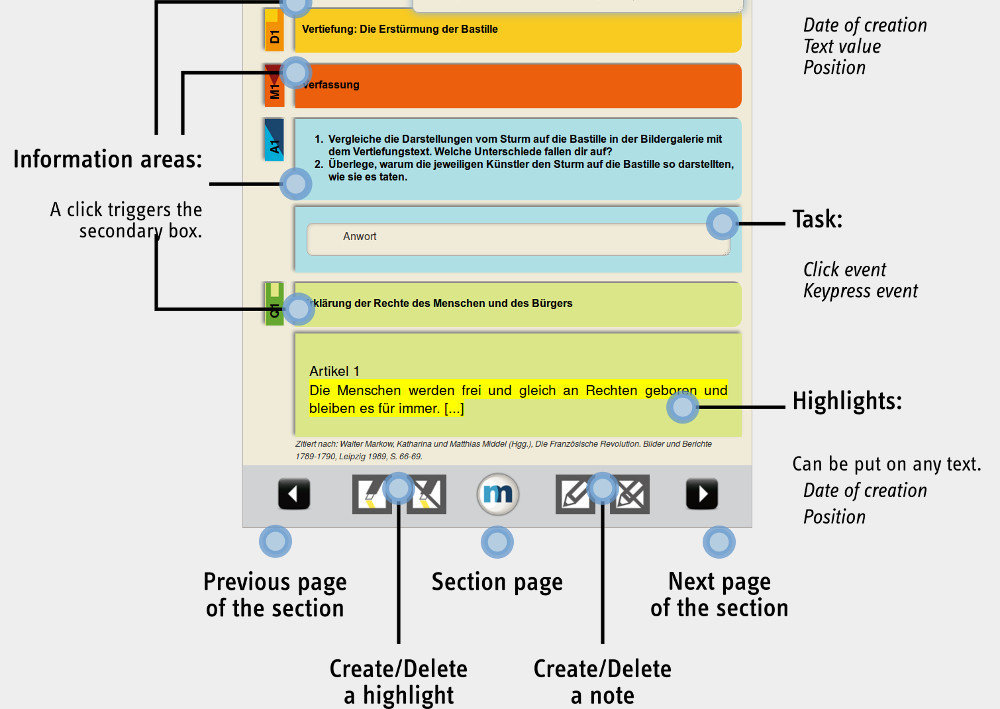
     Markov Chains: Tracking

     Markov Chains: Modeling

     Markov Chains: Clustering

     Markov Chains: Summary

Advantages

Drawbacks

  • Simple,
  • It can handle all the events,
  • It can be complexified.
  • Simple,
  • Tend to overfit if complexified,
  • It does not handle events duration easily.

Global approach

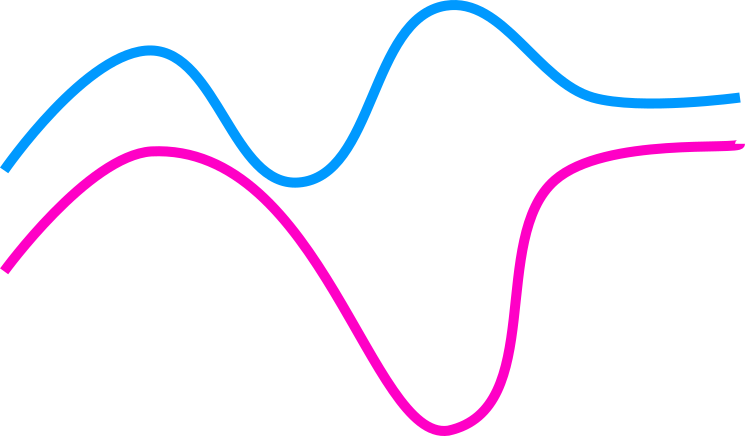
Trajectories

     Trajectories

     Trajectories

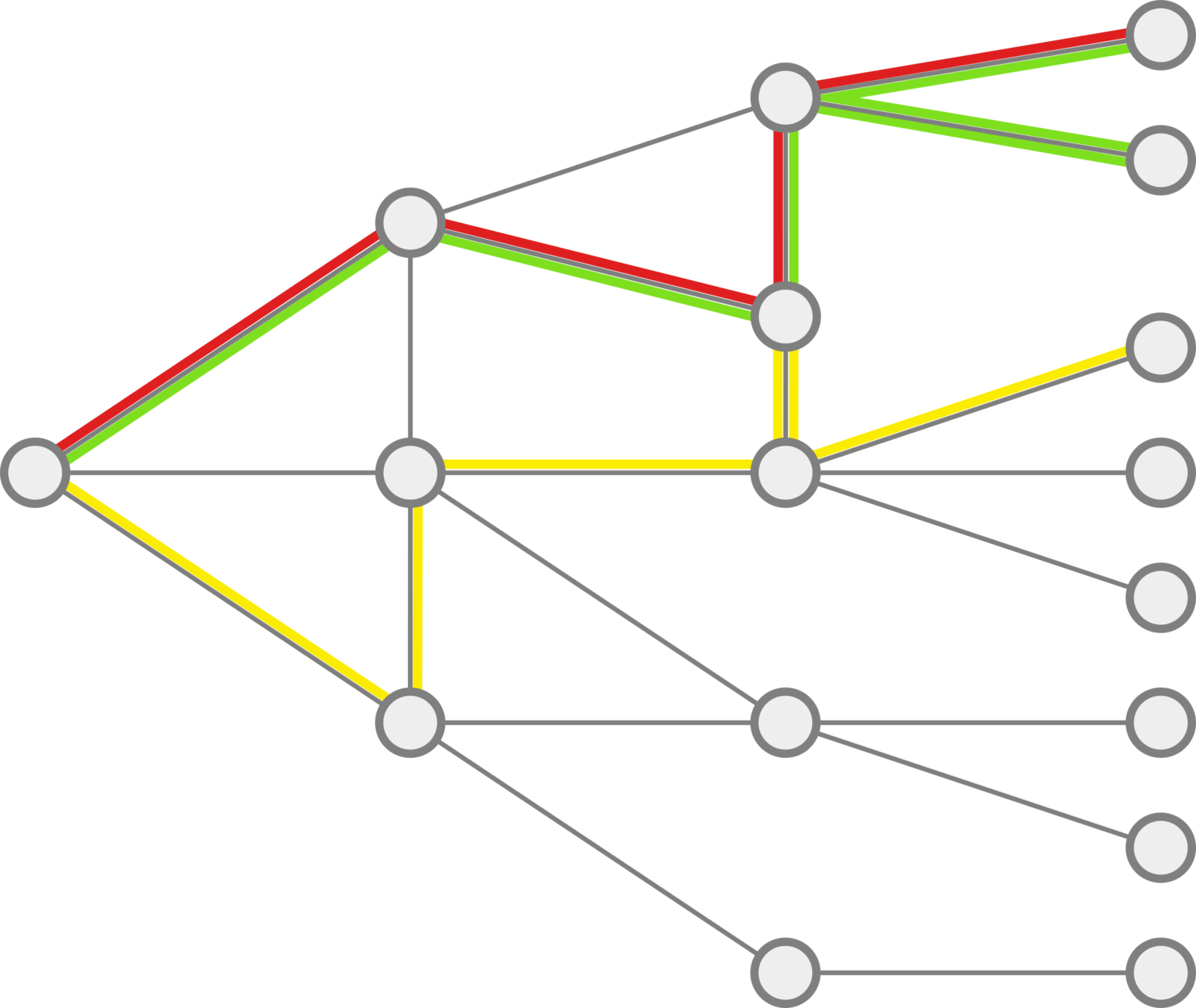
How do we compare paths in a graph?

What do we need:

  • a distance between nodes,
  • a distance between trajectories,

Shortest path

There are many : Hausdorff, DTW...

We transform them into spatial temporal trajectories.

that satisfies three properties.

There are many : Hausdorff, DTW...

Property 1

The distance can compare two trajectories of different durations.

Property 2

The distance is independent of the speed.

Property 3

Repetition of cycles does not modify the distance.

     Hausdorff

d_{\mathrm H}(X,Y) = \max\{\,\sup_{x \in X} \inf_{y \in Y} d(x,y),\, \sup_{y \in Y} \inf_{x \in X} d(x,y)\,\}
dH(X,Y)=max⁡{ sup⁡x∈Xinf⁡y∈Yd(x,y), sup⁡y∈Yinf⁡x∈Xd(x,y) }d_{\mathrm H}(X,Y) = \max\{\,\sup_{x \in X} \inf_{y \in Y} d(x,y),\, \sup_{y \in Y} \inf_{x \in X} d(x,y)\,\}

Let     and     be two non-empty subsets of a metric space.

We define their Hausdorff distance                  by

d_H(X,Y)
dH(X,Y)d_H(X,Y)
X
XX
Y
YY

Definition

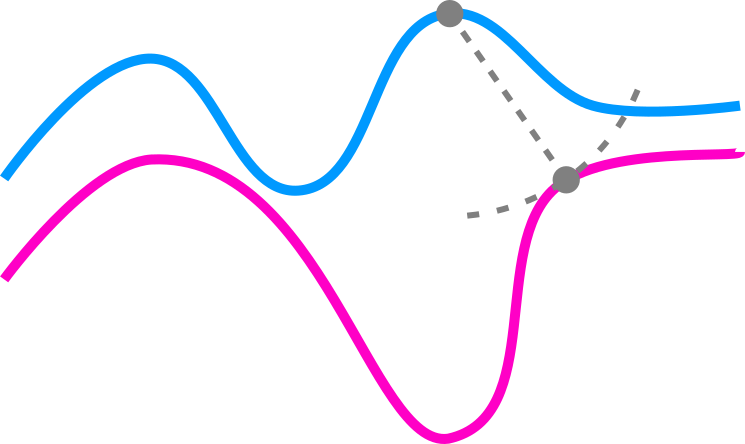
Drawbacks

Outliers govern the distance.

Independent from time/duration.

     Dynamic Time Warping

\begin{array}{l} w_k = (x_i,y_j), \: 1 \leq i \leq N , \: 1\leq j \leq M , \\ w_1 = (x_1,y_1) , \\ w_K = (x_N,y_M) , \\ d(w_k) = d(x_i,y_j), \\ w_k = (x_i,y_j) \Rightarrow w_{k+1} \in \left\lbrace \begin{array}{c} (x_i,y_{j+1}) \\ (x_{i+1},y_{j}) \\ (x_{i+1},y_{j+1}) \end{array} \right\rbrace. \\ \end{array}
wk=(xi,yj), 1≤i≤N, 1≤j≤M,w1=(x1,y1),wK=(xN,yM),d(wk)=d(xi,yj),wk=(xi,yj)⇒wk+1∈{(xi,yj+1)(xi+1,yj)(xi+1,yj+1)}.\begin{array}{l} w_k = (x_i,y_j), \: 1 \leq i \leq N , \: 1\leq j \leq M , \\ w_1 = (x_1,y_1) , \\ w_K = (x_N,y_M) , \\ d(w_k) = d(x_i,y_j), \\ w_k = (x_i,y_j) \Rightarrow w_{k+1} \in \left\lbrace \begin{array}{c} (x_i,y_{j+1}) \\ (x_{i+1},y_{j}) \\ (x_{i+1},y_{j+1}) \end{array} \right\rbrace. \\ \end{array}

Given two trajectories                      and                      , dynamic time warping (DTW) computes an  alignment      

X=(x_i)_N
X=(xi)NX=(x_i)_N
Y=(y_i)_M
Y=(yi)MY=(y_i)_M

Definition

W=(w_k)_K
W=(wk)KW=(w_k)_K

Finally the  distance between     and     is then given by:

X
XX
Y
YY
\mathrm{DTW}(X,Y) = \min_{W} \sum_{k=1}^{|W|} d(w_k).
DTW(X,Y)=min⁡W∑k=1∣W∣d(wk).\mathrm{DTW}(X,Y) = \min_{W} \sum_{k=1}^{|W|} d(w_k).

                       with the following properties:

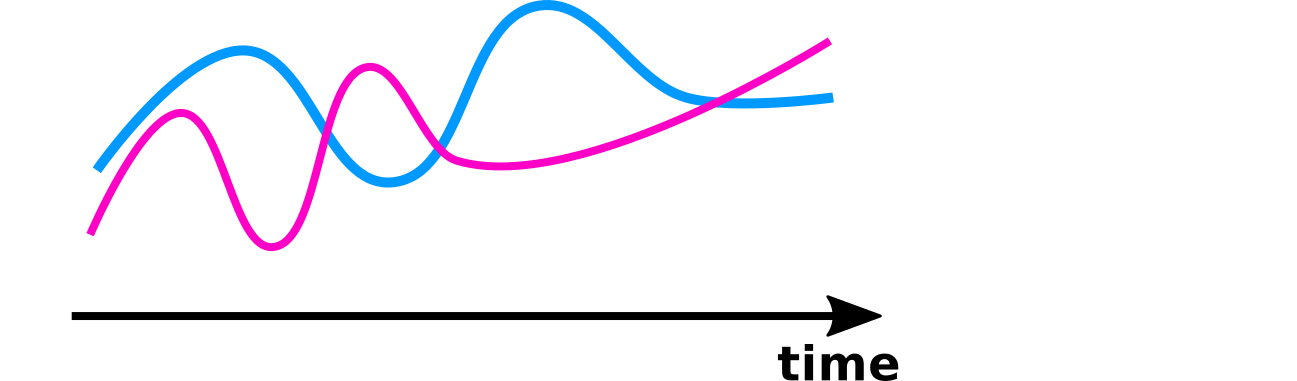
Drawbacks

Very slow.

Temporal order broken.

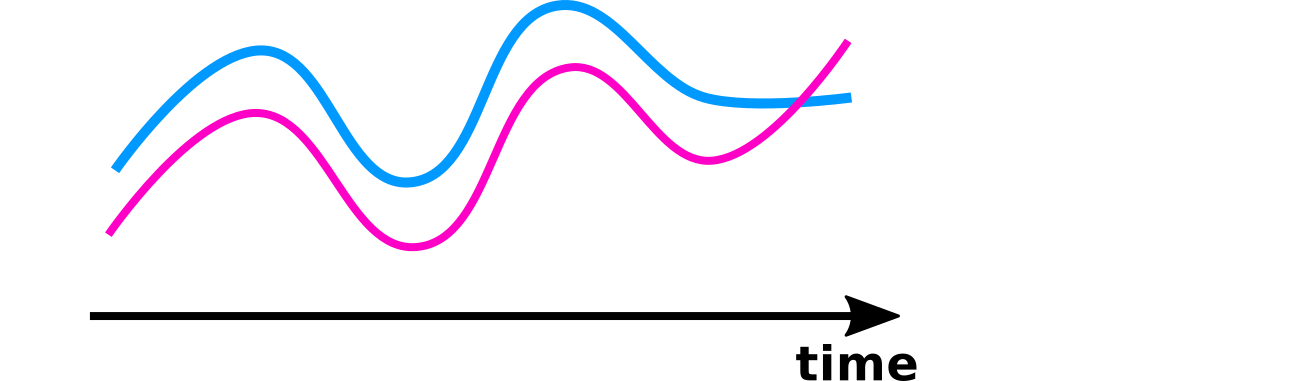
Let's build a distance

     Property 1

Stop the comparison when the shortest trajectory ends.

\Delta(X,Y) \quad \quad = \quad \quad\Delta(X,\mathrm{trunc}(Y))
Δ(X,Y)=Δ(X,trunc(Y))\Delta(X,Y) \quad \quad = \quad \quad\Delta(X,\mathrm{trunc}(Y))

The distance can compare two trajectories of different durations.

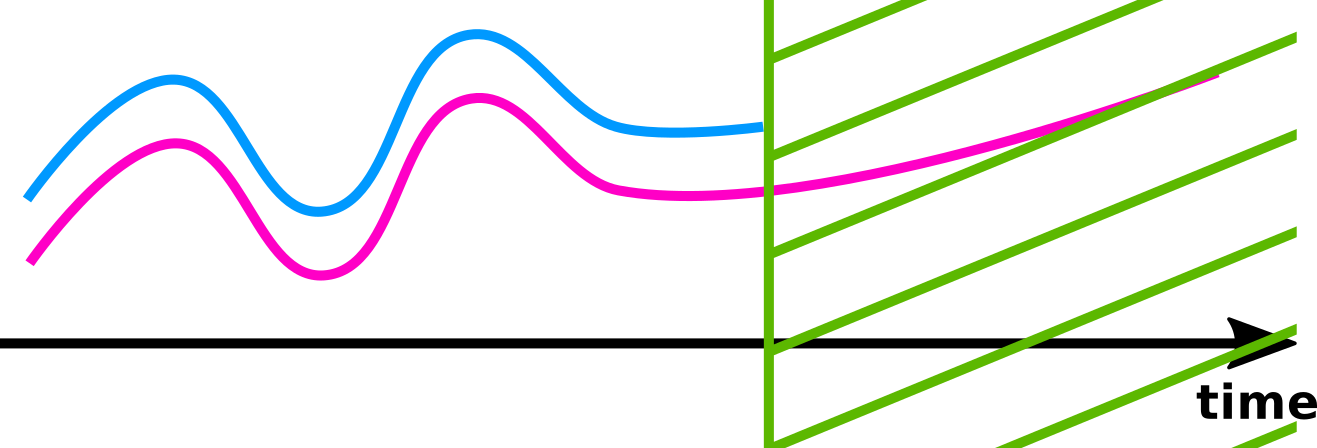
     Property 2

The distance is independent of the speed.

\Delta(X,Y) \quad \quad = \quad \quad\Delta(X',Y')
Δ(X,Y)=Δ(X′,Y′)\Delta(X,Y) \quad \quad = \quad \quad\Delta(X',Y')

Normalize the duration.

     Property 3

Repetition of cycles does not modify the distance.

\Delta(X,Y) \quad \quad = \quad \quad\Delta(X',Y')
Δ(X,Y)=Δ(X′,Y′)\Delta(X,Y) \quad \quad = \quad \quad\Delta(X',Y')

Normalize the duration.

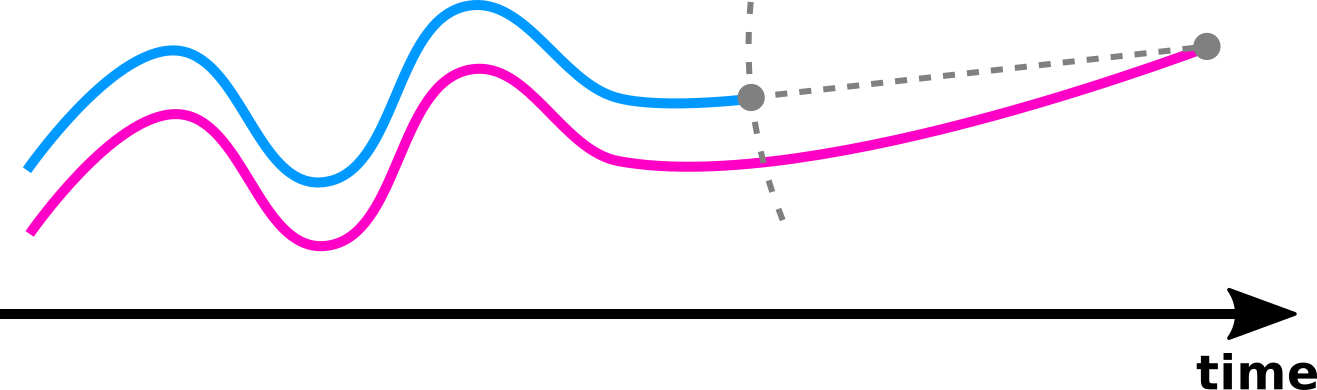
           distance

Definition:

                 is defined as the normalized area spanned between      and      until the shortest one ends.

\Delta
Δ\Delta
\Delta(X,Y)
Δ(X,Y)\Delta(X,Y)
X
XX
Y
YY

Distance comparison

     Comparison

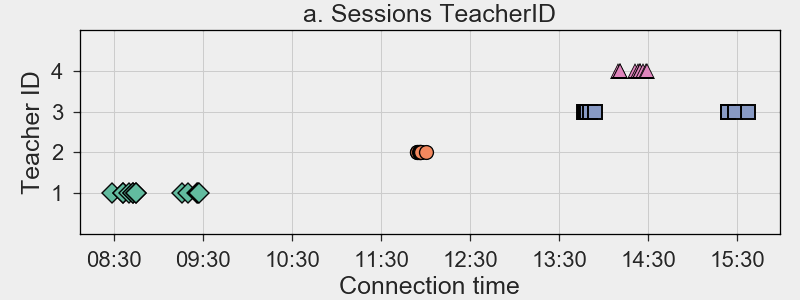
Setting

  • 1 day,
  • 41 session,
  • 37 users,
  • 4 teachers,
  • 6 classes/groups.

WW2

Antiquity

Reformation

Hypothesis

Pupils in the same class, should be grouped together.

Algorithm

k-means with up to 20 clusters.

Hausdorff DTW Delta
# Clusters 8 9 10
Homogeneity 0.39 0.97 0.97
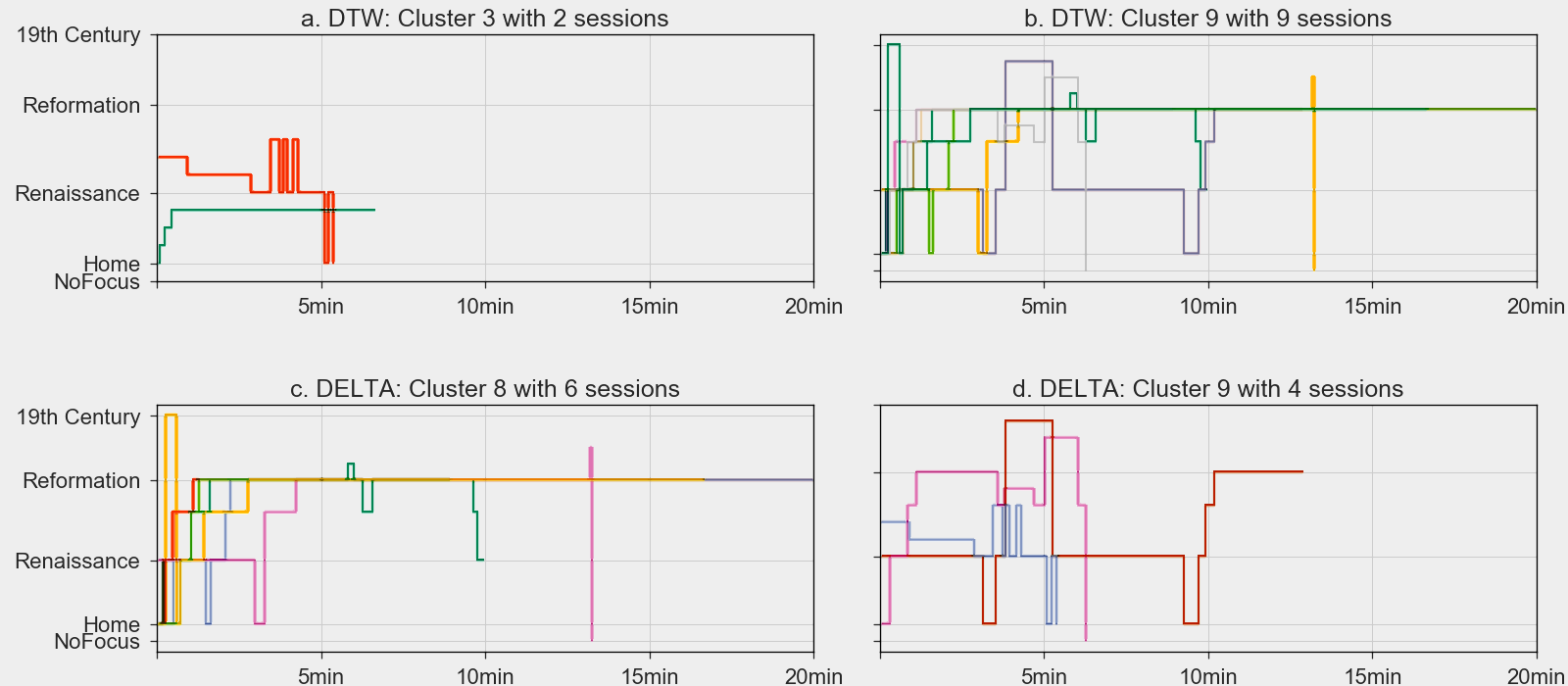
  • Both successfully detects topics.
  •       also detects similar/divergent behaviors.
\Delta
Δ\Delta

Correlations

Can Δ be used as a psychometrics indicator?

Can Δ be used as a teaching style indicator?

     Correlations

Definitions:

\psi_\Delta(u,\mathcal{C})
ψΔ(u,C)\psi_\Delta(u,\mathcal{C})

is the average distance between one pupil     and her classmates during one class session     .

u
uu
\mathcal{C}
C\mathcal{C}
\psi_\Delta(u,\mathcal{C}) = \frac{1}{\#\mathcal{C}}\sum_{c \in \mathcal{C}} \Delta(u,c)
ψΔ(u,C)=1#C∑c∈CΔ(u,c)\psi_\Delta(u,\mathcal{C}) = \frac{1}{\#\mathcal{C}}\sum_{c \in \mathcal{C}} \Delta(u,c)

     Correlations

Five psychometrics scores:

Competency Knowledge Motivation IT Access IT Skills
0.179 0.096 -0.17 0.023 0.092
PPM 0.145 0.133 0.039 -0.002 0.019
EPM 0.184 0.156 -0.065 -0.022 0.063
Competency Knowledge Motivation IT Access IT Skills
-0.224 -0.165 -0.096 -0.069 -0.357
PPM -0.232 0.049 0.111 0.188 -0.156
EPM -0.232 -0.141 -0.142 0.081 0.059
Competency Knowledge Motivation IT Access IT Skills

Activity Indicators

PPM: Pages per minutes

EPM: Events per minutes

         : Average distance between one pupil and her

           classmates

\psi_\Delta
ψΔ\psi_\Delta

Settings:

400 class sessions between Feb. and July 2017.

Two teachers in two different schools.

Teacher B

Teacher A

p-value < 5% marked in bold face

\psi_\Delta
ψΔ\psi_\Delta
\psi_\Delta
ψΔ\psi_\Delta

Correlations

Can Δ be used as a psychometrics indicator?

Yes

Can Δ be used as a teaching style indicator?

     Correlations

Definitions:

\psi_\Delta(u,\mathcal{C})
ψΔ(u,C)\psi_\Delta(u,\mathcal{C})

is the average distance between one pupil     and her classmates during one class session     .

u
uu
\mathcal{C}
C\mathcal{C}
\psi_\Delta(u,\mathcal{C}) = \frac{1}{\#\mathcal{C}}\sum_{c \in \mathcal{C}} \Delta(u,c)
ψΔ(u,C)=1#C∑c∈CΔ(u,c)\psi_\Delta(u,\mathcal{C}) = \frac{1}{\#\mathcal{C}}\sum_{c \in \mathcal{C}} \Delta(u,c)
\Psi_\Delta(\mathcal{C})
ΨΔ(C)\Psi_\Delta(\mathcal{C})

is the average of          during one class session    .

\psi_\Delta
ψΔ\psi_\Delta
\mathcal{C}
C\mathcal{C}
\Psi_\Delta(\mathcal{C}) = \frac{1}{\#\mathcal{C}}\sum_{u \in \mathcal{C}} \psi_\Delta(u,\mathcal{C})
ΨΔ(C)=1#C∑u∈CψΔ(u,C)\Psi_\Delta(\mathcal{C}) = \frac{1}{\#\mathcal{C}}\sum_{u \in \mathcal{C}} \psi_\Delta(u,\mathcal{C})

     Correlations

The greater the more freedom is given to the pupils.

     Correlations

     Correlations

Competency
0.179
PPM 0.145
EPM 0.184
Competency
-0.224
PPM -0.232
EPM -0.232

Teacher B

Teacher A

The difference is significant.

\psi
ψ\psi
\psi
ψ\psi
4.48
5.76
\Psi
Ψ\Psi
\Psi
Ψ\Psi

Pupils diverging from the teaching style perform worst.

All correlations are significant.

Correlations

Can Δ be used as a psychometrics indicator?

Yes

Can Δ be used as a teaching style indicator?

Yes

Yes

Summary

     Summary

  • Track users using spatio-temporal trajectories.
     
  • Built a distance between trajectories:
     
  • Usual clustering algorithms can used
     
  • Interpretable and meaningful clusterings
     
  • Pupils: a    -based indicator correlates with psychometrics scores
     
  • Teachers: a    -based indicator captures teaching style.
\Delta
Δ\Delta
\Delta
Δ\Delta
\Delta
Δ\Delta

Mining User Trajectories

in Electronic Textbooks

 

Ahcène Boubekki

Shailee Jain

Ulf Brefeld

 

Leuphana, Lüneburg

University of Texas at Austin

Leuphana, Lüneburg