Estadística
Dr. Alfredo de Jesús Gutiérrez Gómez
- Presentación
- Temas
- Politicas de clase
- Lineamientos de clase
- Descripción de las actividades
- Actividad de encuadre
- Recomendaciones para la entrega
Contenido
1. Piense en el nombre de un animal que inicie con la primera letra de su nombre.
2. Este no deberá repetirse.
3. Al presentarse deberá completar la siguiente frase: Mi nombre es: _______ y he venido sobre un/a: _______ a la escuela desde _____
4. Dar respuesta a las preguntas:
4.1 ¿Porqué estudio está carrera?
4.2 ¿Qué me ha gustado de la carrera hasta ahora?
Presentación
- Unidad I: Introducción
- Unidad 2: El uso de la distribución y frecuencia en las ciencias sociales
- Unidad 3: Las medidas de tendencia y sus usos
- Unidad 4: Los elementos de la probabilidad.
- Unidad 5: La construcción de un instrumento de medición y el software para procesar el dato estadístico
- Unidad 6: Procesamiento de la información
Temas
- Antecedentes
- Definición
- ¿Qué es la Estadística Descriptiva?
- Definición y uso
- ¿Qué es la Estadística Inferencial?
Unidad I: Introducción
- Los conceptos básicos
- Las variables y su operacionalidad.
- Los tipos de variable
- La distribución de Frecuencia
- Lectura e interpretación de Gráficas
Unidad II: Uso de distribución y frecuencia, en las ciencias sociales
- Media
- Mediana
- Moda
Unidad III: Las medidas de tendencia y su uso
- Los conceptos básicos
- Los tipos
- Sucesos dependientes
- Sucesos independientes
- Sucesos excluyentes y no excluyentes
Unidad IV: Los elementos de la Probabilidad
- Encuesta, cuestionario (otros)
- El uso del Excel
- El uso del SPSS
Unidad V: Construcción de instrumento de medición y Software para procesar el dato estadístico
- La dualidad de la información
- Sistematización de la información
- La interpretación del dato
Unidad VI: Procesamiento de información
- Teléfono móvil en modo silencio.
- Las llamadas urgentes /prio se contestan fuera del salón.
- Turnos de una sola persona para ir al WC.
- Dos faltas a la semana sin justificante perderían derecho a las cuestiones de aprendizaje.
- Levantar la mano para participar.
- Respetar la participación de cada alumno.
- No hay retardos
Políticas de clase
- Mantenerse informado acerca de las lecturas, actividades y tareas del curso asistiendo por lo menos dos veces por semana, durante la duración del curso.
- Cumplir dentro del aula virtual con todas las tareas, foros y actividades detalladas por el programa académico y el profesor, en el tiempo y forma establecidos.
- El incumplimiento de las tareas en tiempo y forma llevarán a una no aprobación del curso
Lineamiento de clase
- Realizar el seguimiento personal desde el Aula Virtual.
- Estar pendiente de los resultados de las evaluación/es parcial/es y final/es.
- Notificar al tutor por escrito, con copia a la coordinación académica, si, por alguna razón excepcional, se encontrara en una circunstancia especial que le impidiera continuar con el curso y recibir así indicaciones de cómo proceder a partir de ese momento.
Lineamiento de clase
- Cuestionario de aprendizaje
- Caso de estudio
Descripción de las actividades
Unidad I
Introducción
- Cuestionario de aprendizaje
- Caso de estudio
Descripción de las actividades
Unidad II
Uso de la distribución y frecuencia en las ciencias sociales
- Cuestionario de aprendizaje
- Caso de estudio
Descripción de las actividades
Unidad III
Las medidas de tendencia y su uso
- Cuestionario de aprendizaje
- Caso de estudio
Descripción de las actividades
Unidad IV
Los elementos de la Probabilidad
- Cuestionario de aprendizaje
- Caso de estudio
Descripción de las actividades
Unidad V
La construcción de un instrumento de medición y el uso del Software para procesar el dato estadístico
- Cuestionario de aprendizaje
- Caso de estudio
Descripción de las actividades
Unidad VI
Procesamiento de información
Instrucciones
- En una hoja escribe la respuesta a las siguientes preguntas
- ¿Qué esperas que se enseñe en este curso?
- ¿A qué te comprometes en este curso?
- ¿Qué deseas aprender en este curso?
Actividad de encuadre
Instrucciones
Una vez contestadas las preguntas anteriores escribir en el foro respectivo la respuesta a cada pregunta.
Actividad de encuadre




Recomendaciónpara la entrega de trabajos / actividades
Recomendaciones
- Portada
- Presentación
- Introducción
- Conclusión
Trabajo
- Mayores a tres líneas
- Menores a ocho líneas
- Coherencia entre párrafos
Párrafos
- Acentuación.
- Evitar redundancia.
- Pleonasmos.
- Mínimo tres errores.
Ortografía - Gramática
- Al menos tres citas dentro del trabajo.
- En formato APA 7ma edición.
Referencia bibliográfica
Recomendaciones
- Fuente Arial.
- Tamaño de título: 14 puntos.
- Tamaño de texto: 12 puntos.
- Interlineado 1.5
- Alineación justificada del texto.
- Los títulos alineados a la izquierda.
- En el encabezado del documento colocar el logotipo del instituto alineado a la derecha. Nombre de la carrera a la izquierda.
Formato del trabajo
Recomendaciones
- Hacerlos en día.
- Exportarlos a jpg / png
Diagramas
- Colocarlos en github.
- En el documento a entregar, colocar el enlace al código.
Códigos fuentes
- Colocarle al pie de la tabla un nombre a la tabla, bajo el siguiente formato: <nombre_tabla numero consecutivo>. <nombre_tabla> <fuente:> <donde_fue_tomada> .
- Colocar un párrafo descriptivo
Tablas
Recomendaciones
- Al menos tres párrafos.
Introducción - conclusión
- Al menos tres fuentes de diversos autores.
- Con sangría francesa al inicio de cuatro espacios.
- Fuente Times New Roman.
- 12 puntos.
- Sin enlaces activos.
Lista de referencias bibliográficas
Recomendaciones
- Colocarle al pie de la imagen / diagrama / gráfica un nombre, bajo el siguiente formato: <nombre_objeto numero consecutivo>. <nombre_objeto> <fuente:> <donde_fue_tomada> .
- Colocar un párrafo donde se describa la imagen / diagrama / gráfica
Imágenes / diagramas / gráficas
¿Dudas?
Comentarios

Unidad I
Introducción
Unidad I: Introducción
Unidad I: Introducción
Estadística
Disciplina matemática que se encarga de recolectar, organizar, analizar e interpretar datos con el fin de describir fenómenos, tomar decisiones informadas y resolver problemas en diversos campos del conocimiento.
Su principal objetivo es entender patrones y variaciones en los datos para responder preguntas y tomar conclusiones basadas en la evidencia.
Unidad I: Introducción
Estadística
Es fundamental porque se aplica en múltiples áreas como la ciencia, economía, ingeniería, medicina, administración, educación y ciencias sociales, entre otras.
A través del análisis estadístico, es posible transformar grandes volúmenes de datos en información útil y comprensible.
Unidad I: Introducción
Estadística
Clasificación
Estadística Descriptiva:
Se enfoca en resumir y representar los datos a través de gráficos, tablas y medidas numéricas como la media, la mediana, la moda y la desviación estándar. Su objetivo es describir los datos de manera clara y concisa.
Ejemplo: Calcular el promedio de calificaciones de un grupo de estudiantes.
Unidad I: Introducción
Estadística
Clasificación
Estadística Inferencial
Utiliza una muestra de datos para hacer inferencias o predicciones sobre una población más amplia. Se apoya en técnicas como la estimación, las pruebas de hipótesis y el análisis de regresión.
Ejemplo: Predecir los resultados de una elección a partir de encuestas realizadas a una muestra representativa de la población.
Unidad I: Introducción
Estadística
Importancia
Facilita la toma de decisiones: Ayuda a tomar decisiones basadas en datos y no en suposiciones.
Permite el análisis de incertidumbre: Proporciona métodos para cuantificar y manejar la incertidumbre.
Ayuda a identificar tendencias: Detecta patrones y tendencias en los datos a lo largo del tiempo.
Unidad I: Introducción
Estadística
Conceptos Claves
Población y muestra: La población es el conjunto completo de elementos a estudiar, mientras que la muestra es un subconjunto representativo de esa población.
Variables: Características que se pueden medir, como el peso, edad o temperatura.
- Cualitativas: No numéricas (colores, género, etc.).
- Cuantitativas: Numéricas (altura, ingresos, etc.).
Parámetros y estadísticos: Los parámetros describen características de la población, y los estadísticos se calculan a partir de la muestra.
Unidad I: Introducción
Estadística
Aplicaciones
- Medicina: Evaluación de la efectividad de nuevos tratamientos.
- Economía y negocios: Análisis de mercado, control de calidad y proyecciones financieras.
- Educación: Evaluación del rendimiento académico.
- Ciencias sociales: Análisis de tendencias en población y comportamiento humano.
Unidad I: Introducción
Actividad de
Aprendizaje
Estadística
Unidad I: Antecedentes
- Su uso inicial estaba vinculado a la administración de recursos, censos poblacionales y toma de decisiones gubernamentales.
- A lo largo del tiempo, ha evolucionado hasta convertirse en una ciencia formal utilizada en múltiples campos.
Estadística
Unidad I: Antecedentes
Civilizaciones antiguas
Origenes >
- Por ejemplo, los egipcios realizaron censos para organizar la construcción de pirámides y calcular impuestos.
- En Babilonia, los registros incluían información sobre cosechas y comercio.
En civilizaciones como Egipto, Babilonia, China e India, se recopilaron datos relacionados con población, agricultura y recursos económicos
Estadística
Unidad I: Antecedentes
Imperio Romano
Origenes >
Los romanos implementaron censos detallados para fines fiscales y militares, registrando datos sobre población, propiedad y riqueza.
La palabra estadística deriva del término “status”, que significa estado en latín, evidenciando su vínculo con la administración gubernamental.
Estadística
Unidad I: Antecedentes
Edad Media y Renacimiento
Origenes >
Durante la Edad Media, la recopilación de datos disminuyó debido a conflictos y cambios políticos.
Durante el Renacimiento, la estadística comenzó a resurgir gracias a los avances en el comercio, la navegación y la organización de los estados.
Siglo XV y XVI: En Europa, surgieron censos con fines tributarios y militares.
John Graunt (1620-1674): Es considerado uno de los precursores de la estadística moderna al analizar registros de mortalidad en Londres para identificar patrones sobre enfermedades y causas de muerte.
Estadística
Unidad I: Antecedentes
Nacimiento de la estadística moderna (Siglos XVII-XVIII)
Origenes >
Siglos XVII y XVIII, la estadística se formalizó como un método cuantitativo para la recolección y análisis de datos:
Blaise Pascal y Pierre de Fermat: Desarrollaron la teoría de la probabilidad, que fue clave para los cálculos estadísticos posteriores.
Gottfried Achenwall (1749): Introdujo el término “estadística” para describir el estudio sistemático de los datos del estado.
Thomas Bayes: Propuso el Teorema de Bayes, fundamental en la probabilidad y la inferencia estadística.
Estadística
Unidad I: Antecedentes
Revolución Industrial (Siglo XIX)
Origenes >
La Revolución Industrial trajo consigo un aumento en la cantidad de datos debido al crecimiento poblacional, económico y tecnológico.
Adolphe Quetelet: Aplicó métodos estadísticos a las ciencias sociales, introduciendo conceptos como el “hombre promedio”.
Florence Nightingale: Usó gráficos estadísticos para evidenciar problemas en los hospitales, lo que ayudó a mejorar la atención médica.
Se consolidaron conceptos como desviación estándar, distribuciones y correlación, fundamentales en la estadística descriptiva e inferencial.
Estadística
Unidad I: Antecedentes
Siglo XX y actualidad
Origenes >
Durante el siglo XX, la estadística se integró a campos como la ciencia, economía, ingeniería y tecnología. Con el desarrollo de las computadoras y la capacidad de manejar grandes volúmenes de datos, la estadística se transformó en una herramienta aún más poderosa.
Surgieron ramas como la estadística inferencial, la bioestadística y la estadística aplicada.
Actualmente, con el avance del Big Data, la inteligencia artificial y el análisis predictivo, la estadística es clave para la toma de decisiones en tiempo real.
Estadística
Unidad I: Antecedentes
Origenes >

Estadística
Unidad I: Definición
La estadística es una ciencia matemática que se encarga de recolectar, organizar, analizar e interpretar datos con el fin de describir fenómenos, tomar decisiones informadas y resolver problemas en distintos campos del conocimiento.
- Su objetivo principal es entender patrones y variaciones en los datos, facilitando conclusiones basadas en evidencia.
Estadística
Unidad I: Definición
Recolección de datos
> Aspectos Claves
Consiste en obtener información mediante censos, encuestas, experimentos u observaciones.
Ejemplo: Realizar una encuesta para conocer la opinión pública sobre un tema.
Estadística
Unidad I: Definición
Organización de datos
> Aspectos Claves
Los datos recolectados se organizan en tablas o gráficos que facilitan su comprensión y análisis.
- Ejemplo: Tablas de frecuencia o gráficos de barras.
Estadística
Unidad I: Definición
Análisis de datos
> Aspectos Claves
Se aplican métodos y técnicas estadísticas para examinar los datos y descubrir tendencias, patrones o relaciones.
- Ejemplo: Calcular medidas como la media, mediana o desviación estándar.
Estadística
Unidad I: Definición
Interpretación de resultados
> Aspectos Claves
A partir del análisis, se extraen conclusiones que permiten tomar decisiones o realizar predicciones.
- Ejemplo: Interpretar los resultados de una encuesta para lanzar un nuevo producto.
Estadística
Unidad I: Definición
Ramas de la estadística
> Aspectos Claves
Estadística descriptiva: Se enfoca en resumir y representar los datos (tablas, gráficos, medidas numéricas).
Estadística inferencial: Utiliza muestras para hacer predicciones o generalizaciones sobre una población más amplia.
Estadística
Unidad I: Definición
Conceptos fundamentales
> Aspectos Claves
Población: Conjunto total de individuos o elementos a estudiar.
Muestra: Subconjunto representativo de la población.
Variable: Característica medible (puede ser cualitativa o cuantitativa).
Parámetro: Medida que describe a la población.
Estadístico: Medida calculada a partir de la muestra.
Estadística
Unidad I: Definición
> Aspectos Claves

Unidad I: Estadística Descriptiva
¿Qué es la estadística descriptiva?
Rama de la estadística que se encarga de resumir, organizar y representar datos de manera clara y concisa.
Su objetivo principal es describir las características de un conjunto de datos, facilitar su comprensión mediante medidas numéricas, tablas y representaciones gráficas.
No realiza inferencias ni predicciones sobre una población más amplia; solo describe y analiza los datos recolectados.
Unidad I: Estadística Descriptiva
Usos de la estadística descriptiva
- Resumir grandes volúmenes de información en formas más manejables y entendibles.
- Detectar tendencias y patrones en un conjunto de datos
- Describir datos cuantitativos (números) y cualitativos (categorías)
- Facilitar la toma de decisiones basadas en datos claros y concretos
- Preparar datos para análisis más complejos o estadística inferencial.
Unidad I: Estadística Descriptiva
Aplicaciones de la estadística descriptiva
Educación
Evaluar el rendimiento académico de un grupo de estudiantes mediante promedios, distribuciones y gráficos.
Negocios
Analizar ventas, ingresos y gastos para identificar tendencias y patrones.
Economía
Evaluar el rendimiento financiero de una empresa a través de indicadores numéricos.
Unidad I: Estadística Descriptiva
Aplicaciones de la estadística descriptiva
Medicina
Resumir datos de estudios médicos, como la presión arterial promedio de un grupo de pacientes.
C. sociales
Analizar encuestas sobre opiniones o características demográficas de una población.
Deportes
Calcular estadísticas como promedios de rendimiento de jugadores o equipos.
Ingeniería y control de calidad
Monitorear el desempeño de productos y detectar desviaciones en los procesos de producción.
Unidad I: Estadística Descriptiva
Herramientas y conceptos de la estadística descriptiva
Medidas de tendencia central
Media
Promedio de los valores.
Mediana
Valor central en un conjunto de datos ordenados.
Moda
Valor que más se repite en un conjunto de datos.
Unidad I: Estadística Descriptiva
Herramientas y conceptos de la estadística descriptiva
Medidas de dispersión o variabilidad
Rango
Diferencia entre el valor máximo y mínimo.
Varianza
Promedio de las desviaciones al cuadrado respecto a la media.
Desviación estándar
Mide cuánto se alejan los datos del promedio.
Unidad I: Estadística Descriptiva
Herramientas y conceptos de la estadística descriptiva
Tablas y gráficos
Tablas de frecuencia
Resumen de datos organizados por categorías o rangos.
Gráficos de barras
Representación visual de datos cualitativos o cuantitativos.
Histogramas
Gráficos para representar la distribución de datos cuantitativos
Gráficos circulares
Muestran proporciones de un todo.
Unidad I: Estadística Descriptiva
Ejemplo de la estadística descriptiva
Un profesor recopila las calificaciones de un examen de matemáticas para 10 estudiantes: Datos: 7, 8, 9, 6, 7, 8, 7, 9, 6, 8.
Media
La media de las calificaciones es 7.5.
Mediana
Se ordena los datos (6, 6, 7, 7, 7, 8, 8, 8, 9, 9).
La mediana es 7.5 (valor central entre el 5º y 6º dato).
Moda
El valor 7 y el 8 se repiten más veces; son las modas.
Unidad I: Estadística Descriptiva
Ejemplo de la estadística descriptiva
Un profesor recopila las calificaciones de un examen de matemáticas para 10 estudiantes: Datos: 7, 8, 9, 6, 7, 8, 7, 9, 6, 8.
Media
La media de las calificaciones es 7.5.
Mediana
Se ordena los datos (6, 6, 7, 7, 7, 8, 8, 8, 9, 9).
La mediana es 7.5 (valor central entre el 5º y 6º dato).
Moda
El valor 7 y el 8 se repiten más veces; son las modas.
Unidad I: Estadística Descriptiva
Ejemplo de la estadística descriptiva
Un profesor recopila las calificaciones de un examen de matemáticas para 10 estudiantes: Datos: 7, 8, 9, 6, 7, 8, 7, 9, 6, 8.
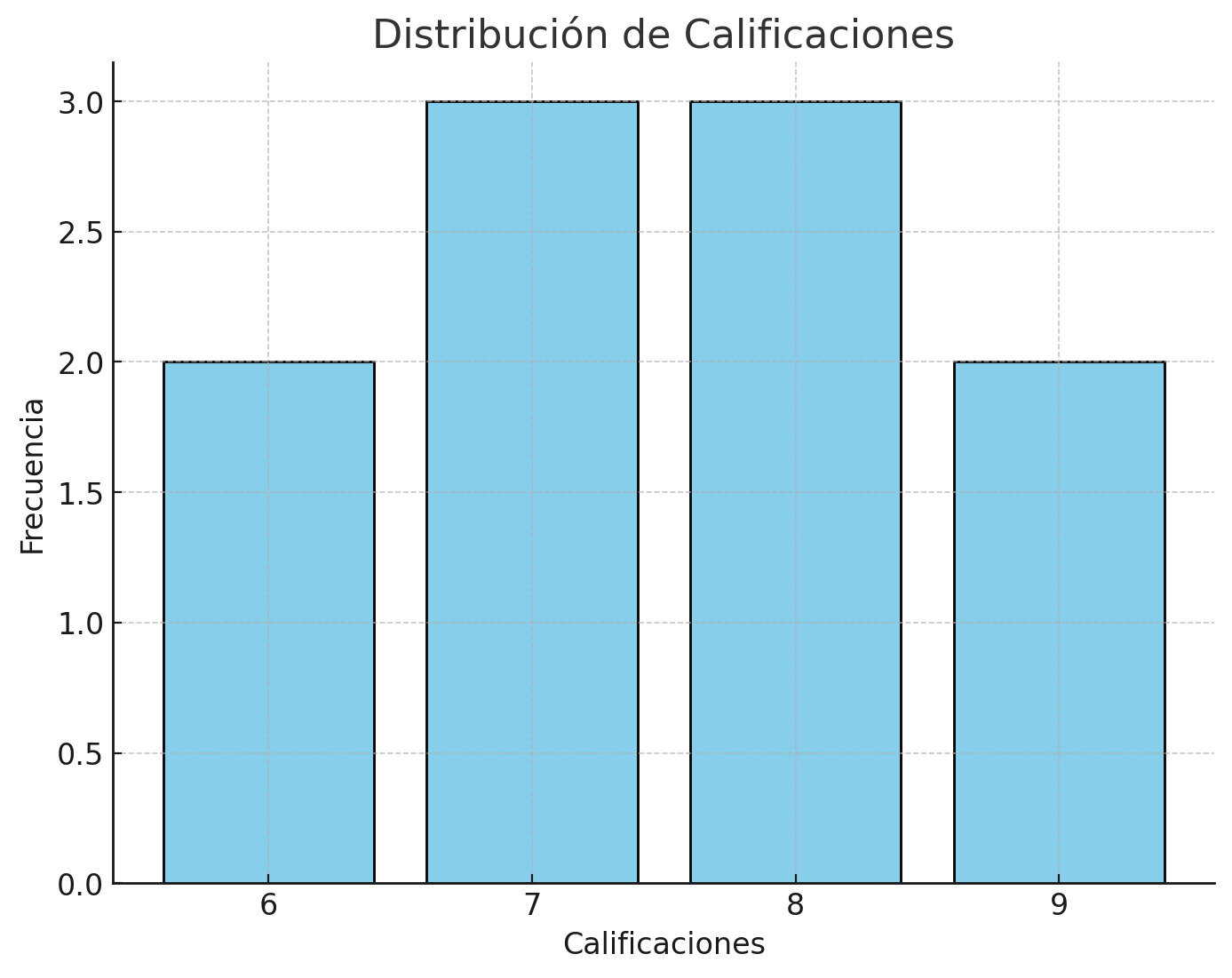
Unidad I: Estadística Descriptiva
Actividad de Aprendizaje

Unidad I: Estadística Inferencial
¿Qué es?
Se encarga de hacer predicciones, estimaciones o generalizaciones sobre una población a partir del análisis de una muestra de datos.
Utiliza herramientas matemáticas y probabilísticas para extraer conclusiones que van más allá de los datos recolectados directamente.
A diferencia de la estadística descriptiva, que solo organiza y resume datos, la estadística inferencial permite inferir información desconocida de una población basándose en datos parciales.
Unidad I: Estadística Inferencial
Definición
Se define como el conjunto de técnicas y métodos utilizados para analizar una muestra de datos con el objetivo de hacer inferencias o predicciones sobre el comportamiento de una población completa.
Estas inferencias se apoyan en modelos probabilísticos y permiten cuantificar el nivel de incertidumbre asociado.
Unidad I: Estadística Inferencial
Usos
- Hacer predicciones: Permite prever resultados futuros con base en datos actuales.
- Tomar decisiones: Facilita decisiones informadas al estimar parámetros desconocidos de una población.
- Comparar grupos: Analiza si existen diferencias significativas entre distintos conjuntos de datos.
- Probar hipótesis: Verifica afirmaciones o suposiciones mediante pruebas estadísticas.
- Generalizar resultados: Extiende las conclusiones obtenidas de una muestra al total de la población.
Unidad I: Estadística Inferencial
Aplicaciones
Medicina
- Evaluar la efectividad de un tratamiento mediante muestras representativas de pacientes.
- Ejemplo: Determinar si un nuevo medicamento reduce la presión arterial en una población.
Ciencias sociales
- Analizar encuestas para predecir resultados electorales o tendencias sociales.
- Ejemplo: Estimar la intención de voto en una elección con base en una encuesta a una muestra representativa.
Unidad I: Estadística Inferencial
Aplicaciones
Negocios y economía
- Predecir la demanda de un producto, analizar tendencias de ventas o evaluar mercados.
- Ejemplo: Estimar el crecimiento de ventas en el próximo trimestre a partir de datos históricos.
Industria y control de calidad
- Evaluar si un proceso de producción cumple con estándares de calidad.
- Ejemplo: Analizar muestras de productos para predecir si toda la producción tiene defectos.
Unidad I: Estadística Inferencial
Aplicaciones
Educación
- Medir el rendimiento académico de los estudiantes a nivel nacional mediante pruebas muestrales.
Ciencia e investigación
- Realizar estudios experimentales para validar hipótesis científicas
Unidad I: Estadística Inferencial
Métodos Principales
Estimación de parámetros
Permite calcular valores aproximados de parámetros desconocidos de una población (como la media o proporción) usando datos muestrales.
Ejemplo: Estimar el ingreso promedio de una población basándose en una muestra de hogares.
Unidad I: Estadística Inferencial
Métodos Principales
Pruebas de hipótesis
Consisten en comprobar afirmaciones sobre parámetros de la población mediante análisis probabilísticos.
Ejemplo: Probar si la media de calificaciones de una escuela es mayor a la de otra escuela.
Unidad I: Estadística Inferencial
Métodos Principales
Intervalos de confianza
Rango de valores que se construye a partir de datos muestrales y que contiene con cierto nivel de confianza al parámetro poblacional.
Ejemplo: "La proporción de personas que votará por un candidato está entre el 45% y 50% con un 95% de confianza".
Unidad I: Estadística Inferencial
Métodos Principales
Análisis de regresión
Permite analizar la relación entre variables y hacer predicciones.
Ejemplo: Predecir las ventas de un negocio según su inversión en publicidad.
Unidad I: Estadística Inferencial
Métodos Principales
Distribuciones de probabilidad
Modelos matemáticos que describen cómo se distribuyen los datos dentro de una población.
Unidad I: Estadística Inferencial
Ejemplo
Un investigador desea saber si los estudiantes de una universidad tienen, en promedio, un coeficiente intelectual (CI) mayor a 100. Como no puede medir a toda la población universitaria, selecciona una muestra de 50 estudiantes.
- Datos: La muestra arroja un CI promedio de 102 con una desviación estándar de 15.
- Aplicación: Se utiliza una prueba de hipótesis para determinar si el CI promedio de la universidad es significativamente mayor a 100.
- Resultado: Si el valor-p de la prueba es pequeño (por ejemplo, menor a 0.05), se concluye que el CI promedio de los estudiantes es mayor a 100 con un nivel de confianza del 95%.
Unidad I: Estadística Inferencial
Actividad de aprendizaje





Unidad II
El uso de la distribución y frecuencia en las ciencias sociales
Unidad II: Distribución y frecuencia en C.S.
Unidad II: Distribución y frecuencia en C.S.
Distribución: En estadística, se refiere a la forma en que se organizan los valores de una variable dentro de un conjunto de datos. Puede presentarse en forma de tablas, gráficos o representaciones matemáticas.
Unidad II: Distribución y frecuencia en C.S.
Frecuencia: Es el número de veces que un valor específico aparece en un conjunto de datos. Se divide en:
Número total de veces que ocurre un valor.
Frecuencia absoluta
Proporción de una frecuencia respecto al total de datos.
Frecuencia relativa
Suma progresiva de las frecuencias absolutas.
Frecuencia acumulada
Unidad II: Distribución y frecuencia en C.S.
Importancia
En las ciencias sociales, el análisis de la distribución y frecuencia es fundamental para estudiar tendencias, comportamientos y fenómenos sociales.
A través de estas herramientas estadísticas, se puede entender mejor la realidad social y tomar decisiones informadas.
Unidad II: Distribución y frecuencia en C.S.
Aspectos claves
Organización de datos
Permite ordenar la información recopilada de estudios sociales, como encuestas o censos.
Visualización de patrones
Facilita la identificación de patrones o tendencias mediante gráficos ( histogramas, diagramas de barras).
Comparación de grupos
Ayuda a comparar datos entre distintos grupos sociales (género, edad, nivel socioeconómico, etc.).
Toma de decisiones
Proporciona evidencia objetiva para la formulación de políticas públicas y programas sociales.
Unidad II: Distribución y frecuencia en C.S.
Usos
Estudios Demográficos
e analizan frecuencias para conocer la composición de una población ( edad, género o ubicación).
Sociología
Permite estudiar fenómenos como el nivel de educación, empleo, o ingreso de distintos sectores de la sociedad. (Distribución de variables sociales)
Psicología Social
Se analiza la frecuencia de conductas o actitudes en una muestra representativa
Unidad II: Distribución y frecuencia en C.S.
Herramientas
Tablas de frecuencia
Organizan los datos y muestran la cantidad de veces que ocurre un valor.
Histogramas
Permite estudiar el rendimiento académico, asistencia escolar o distribución de recursos educativos.
Diagramas de barras
Visualizan datos categóricos y permiten comparar frecuencias entre grupos.
Polígonos de frecuencia
Conectan puntos que representan las frecuencias de los valores en un gráfico lineal.
Unidad II: Distribución y frecuencia en C.S.
Actividad de aparendizaje

Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
En estadística y ciencias sociales, una variable es una característica o atributo que puede adoptar diferentes valores. Estos valores pueden ser numéricos o cualitativos y son medidos, observados o analizados en un estudio.
Ejemplo: Edad, nivel de ingreso, género, nivel educativo, horas_trabajadas.
Las variables son la base para recolectar datos en investigaciones sociales, permitiendo organizar y analizar la información mediante métodos estadísticos como la distribución y la frecuencia.
Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
Clasificación de las Variables
Variables Cualitativas
Estas variables describen características no numéricas o cualidades. No se pueden medir en escalas numéricas, pero sí clasificar o categorizar.
- Género: Masculino, Femenino, Otro.
- Estado civil: Soltero, Casado, Divorciado.
- Opinión: Positiva, Neutral, Negativa.
Nominales
Ordinales
No existe un orden lógico (Ej.: colores, nombres).
Existe un orden o jerarquía (Ej.: bajo, medio, alto).
Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
Clasificación de las Variables
Variables Cuantitativas
Estas variables adoptan valores numéricos y permiten realizar operaciones matemáticas como sumar o promediar.
- Edad: 18, 25, 35 años.
- Ingreso mensual: $500, $1,200, $3,000.
- Número de hijos: 0, 1, 2, 3.
Nominales
Ordinales
Toman valores enteros (Ej.: número de personas en una familia).
Pueden tomar valores en un intervalo infinito, incluidos decimales (Ej.: peso, altura, temperatura).
Unidad II: Distribución y frecuencia en C.S.
Actividad de Aprendizaje
- El nivel educativo de un grupo de personas se clasifica como: primaria, secundaria, o superior.
- El peso (en kilogramos) de una muestra de atletas.
- La cantidad de hijos que tienen las familias en una comunidad.
- El estado civil de una población (soltero, casado, divorciado, viudo).
- El ingreso mensual (en dólares) de trabajadores de una empresa.
- La temperatura registrada diariamente en una ciudad (en grados Celsius).
- Los colores favoritos de un grupo de estudiantes.
- El grado de satisfacción de los usuarios con un servicio, evaluado como: bajo, medio, alto.
- El número de libros leídos por estudiantes en un año.
Unidad II: Distribución y frecuencia en C.S.
Actividad de Aprendizaje
Para cada enunciado, determina lo siguiente:
- Tipo de variable: Cualitativa o Cuantitativa.
- Subtipo: Nominal, Ordinal, Discreta o Continua.
Ejemplo de respuesta:
- Enunciado 1: Nivel educativo → Variable cualitativa ordinal.
- Enunciado 2: Peso → Variable cuantitativa continua.
Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
La operacionalización de las variables consiste en definir cómo se van a medir y representar las variables en un estudio estadístico.
Es un paso esencial para vincular conceptos abstractos con datos observables y medibles.
Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
Pasos para operacionalizar una variable
- Definir la variable: Establecer qué se va a medir.
- Categorizar o cuantificar: Convertir la variable en indicadores concretos y medibles.
- Seleccionar unidades de medida: Decidir si se medirán en valores numéricos (años, pesos) o categorías (nivel educativo: primaria, secundaria).
Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
Pasos para operacionalizar una variable
-
Establecer la escala:
- Nominal: Solo clasifica.
- Ordinal: Ordena por jerarquía.
- Intervalo: Permite diferencias entre valores (Ej.: temperatura).
- Razón: Tiene un cero absoluto y permite comparaciones (Ej.: ingresos).
Unidad II: Distribución y frecuencia en C.S.
Variables y su operacionalidad
Ejemplo para operacionalizar una variable
- Variable abstracta: Nivel socioeconómico.
-
Indicadores concretos:
- Ingreso mensual (numérico).
- Nivel educativo alcanzado (categoría).
- Acceso a servicios básicos (sí o no).
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
- Definir la variable: Explica qué se quiere medir.
- Categorizar o cuantificar: Propón indicadores concretos para medirla.
- Seleccionar unidades de medida: Determina si será numérica o categórica.
- Establecer la escala: Decide si es nominal, ordinal, intervalo o razón.
A continuación, se presenta un conjunto de conceptos abstractos comunes en estudios sociales. Tu tarea es operacionalizar cada uno siguiendo los pasos indicados:
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
- Bienestar emocional: Queremos medir el estado emocional de un grupo de personas.
- Nivel educativo: Analizar la relación entre nivel educativo y oportunidades laborales.
- Hábito de lectura: Evaluar la frecuencia con la que las personas leen libros.
- Acceso a servicios de salud: Identificar la calidad del acceso a la salud en diferentes comunidades.
- Participación ciudadana: Cuantificar el grado de participación en procesos electorales.
- Satisfacción laboral: Medir el nivel de satisfacción de empleados en una empresa.
Conceptos Abstractos para Operacionalizar:
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
- Definición de la variable.
- Indicadores concretos.
- Unidades de medida.
- Escala de medición.
Lo que se espera:
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
Lo que se espera:
Ejemplo de respuesta:
-
Concepto Abstracto: Bienestar emocional.
- Definición: Medir el estado emocional positivo o negativo de las personas.
- Indicadores concretos: Frecuencia de emociones positivas, nivel de estrés, calidad del sueño.
- Unidades de medida: Escala del 1 al 10, número de horas de sueño.
- Escala: Ordinal para la escala de emociones; razón para horas de sueño.
Unidad II: Distribución y frecuencia en C.S.
Tipos de variables
Una variable es cualquier característica, atributo o propiedad que puede tomar diferentes valores o categorías en un grupo de estudio.
Estos valores pueden ser numéricos o cualitativos, y cambian según los sujetos o elementos analizados.
Unidad II: Distribución y frecuencia en C.S.
Tipos de variables
Variable Cualitativa
Nominal
Ordinal
No tienen un orden lógico
Tienen un orden o jerarquía, pero las diferencias entre categorías no son numéricamente iguales.
Variable Cualitativa
Nominal
Ordinal
Género (masculino, femenino, otro).
Nivel socioeconómico (bajo, medio, alto).
Describen características o atributos que no se miden numéricamente. En lugar de números, sus valores son categorías o etiquetas.
Unidad II: Distribución y frecuencia en C.S.
Tipos de variables
Variable Cuantitativa
Continuas
Discretas
Toman valores enteros (no hay valores intermedios entre ellos).
Pueden tomar cualquier valor dentro de un intervalo, incluidos los decimales.
Variable Cuantitativa
Continuas
Discretas
Número de hijos en una familia.
Altura en centímetros (168.5 cm).
Miden numéricamente y permiten operaciones matemáticas como sumar, restar o calcular promedios.
Unidad II: Distribución y frecuencia en C.S.
Actividad de Aprendizaje
A continuación, se presenta una lista de situaciones extraídas de contextos de las ciencias sociales. Identifica el tipo de variable (cualitativa o cuantitativa) y, si corresponde, el subtipo (nominal, ordinal, discreta o continua).
Unidad II: Distribución y frecuencia en C.S.
Actividad de Aprendizaje
- Género de los participantes en un estudio sobre empleo (masculino, femenino, otro).
- Edad de los encuestados medida en años.
- Nivel de satisfacción con un servicio público, clasificado como: insatisfecho, neutral, satisfecho.
- Número de hijos en familias de una comunidad rural.
- Ingreso mensual de los hogares, registrado en dólares.
- Religión practicada por los habitantes de una ciudad (católica, protestante, judía, ninguna).
- Tiempo de desplazamiento al trabajo, medido en minutos.
- Estado civil de los encuestados (soltero, casado, divorciado, viudo).
Unidad II: Distribución y frecuencia en C.S.
Actividad de Aprendizaje
- Frecuencia de ejercicio físico semanal, categorizada como: nunca, ocasional, regular, diaria.
- Tamaño de la familia, definido como el número total de integrantes.
- Altura de los estudiantes en una escuela secundaria, medida en metros.
- Clase social percibida, definida como baja, media o alta
Unidad II: Distribución y frecuencia en C.S.
Actividad de Aprendizaje
Lo que se espera
- Tipo de variable: Cualitativa o Cuantitativa.
- Subtipo: Nominal, Ordinal, Discreta o Continua.
Enunciado 1:
- Variable: Género.
- Tipo: Cualitativa.
- Subtipo: Nominal.
Enunciado 2:
- Variable: Edad.
- Tipo: Cuantitativa.
- Subtipo: Continua.
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
la distribución de frecuencia es una herramienta esencial de la estadística descriptiva utilizada para organizar y resumir datos.
Permite representar de manera clara cómo se distribuyen las observaciones o mediciones de una variable dentro de una población o muestra.
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
Una distribución de frecuencia es una tabla o gráfico que muestra el número de veces (frecuencia) que ocurren diferentes valores o rangos de valores en un conjunto de datos.
Es particularmente útil para identificar patrones, tendencias y anomalías en los datos sociales.
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
Frecuencia Absoluta (f)
El número de veces que un valor específico ocurre
Frecuencia Relativa (fr)
La proporción o porcentaje de cada frecuencia absoluta respecto al total.
Frecuencia Acumulada (F)
La suma progresiva de las frecuencias absolutas.
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
Variable Analizada
Puede ser cualitativa o cuantitativa, dependiendo del fenómeno social estudiado.
Clases o Categorías
Los valores o rangos que agrupan las observaciones.
Frecuencia
La cantidad de observaciones dentro de cada clase o categoría.
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
Recolección de Datos
Recopilar información de la población o muestra.
Organización
Identificar las categorías o intervalos de la variable a estudiar.
Conteo de Frecuencias
Determinar cuántas observaciones caen en cada categoría o intervalo.
1
2
3
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
Cálculo de Frecuencias Relativas y Acumuladas
Si es necesario, calcular porcentajes y sumas progresivas.
Visualización
Presentar los resultados en gráficos como histogramas, polígonos de frecuencia o diagramas de barras.
4
5
Unidad II: Distribución y frecuencia en C.S.
La distribución de Frecuencia
| Intervalo de Ingresos ($) | Frecuencia Absoluta (f) | Frecuencia Relativa (%) | Frecuencia Acumulada (F) |
|---|---|---|---|
| Menos de $1,000 | 20 | 20% | 20 |
| $1,000 - $2,000 | 30 | 30% | 50 |
| $2,001 - $3,000 | 25 | 25% | 75 |
| Más de $3,000 | 25 | 25% | 100 |
Tabla 1. Estudio de la distribución de Ingresos Mensuales en una Comunidad
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
Un sociólogo realizó una encuesta a 50 familias en una comunidad para analizar su ingreso mensual (en dólares). Los datos recopilados son los siguientes
1200, 1500, 1800, 2000, 2200, 2400, 2500, 2700, 1500, 1800,
2000, 1200, 1500, 2200, 2400, 1200, 2700, 2000, 2500, 2200,
1500, 1800, 2000, 2400, 2500, 2700, 1800, 2000, 2200, 2400,
1200, 1500, 2500, 2700, 2000, 1500, 1800, 2200, 2400, 1500,
2500, 2700, 2000, 2200, 2400, 1200, 1500, 1800, 2500, 2700.
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
Instrucciones
- Clasificación en Intervalos: Organiza los ingresos en intervalos de amplitud 500 (por ejemplo: 1200-1699, 1700-2199, etc.).
- Frecuencia Absoluta: Cuenta cuántos valores caen en cada intervalo.
- Frecuencia Relativa: Calcula la proporción de cada intervalo respecto al total.
- Frecuencia Acumulada: Suma progresivamente las frecuencias absolutas de cada intervalo.
- Representación Gráfica: Construye un histograma basado en la tabla creada.
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
| Intervalo de Ingresos ($) | Frecuencia Absoluta (f) | Frecuencia Relativa (%) | Frecuencia Acumulada (F) |
|---|---|---|---|
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
-
¿Cuál es el intervalo con mayor frecuencia?
-
¿Qué porcentaje de familias tiene ingresos menores a $2200?
El histograma se construirá con los intervalos en el eje X y la frecuencia absoluta en el eje Y.
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Es una habilidad esencial en las ciencias sociales, ya que permite analizar y comunicar información obtenida a través de la distribución y frecuencia de datos.
Estas herramientas gráficas son fundamentales para representar patrones, tendencias y relaciones entre variables, facilitando la toma de decisiones y el diseño de políticas basadas en evidencia.
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Definición: La lectura de gráficas implica identificar los elementos clave que componen una representación gráfica (ejes, datos, categorías, intervalos). La interpretación consiste en extraer conclusiones significativas sobre el fenómeno social estudiado a partir de la información presentada.
Objetivo: Comprender datos de forma visual para detectar tendencias, relaciones, variaciones y distribuciones en un contexto específico.
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Gráfico de Barras
Representa datos categóricos con barras cuya longitud es proporcional a la frecuencia.
Histograma
Muestra la distribución de frecuencias de una variable cuantitativa agrupada en intervalos.
Gráfico Circular (Pastel)
Representa proporciones o porcentajes de categorías respecto al total.
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Polígono de Frecuencia
Representa datos cuantitativos conectando puntos que indican frecuencias para cada intervalo.
Gráfica de Líneas
Muestra tendencias a lo largo del tiempo.
Diagrama de Dispersión
Representa la relación entre dos variables cuantitativas.
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Ejes
Variable en el eje X (independiente) y eje Y (dependiente)
Unidades
Escalas e intervalos usados en los ejes.
Leyendas y Títulos
Información clave sobre qué representa la gráfica.
Identificar los Elementos Básicos
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Identificar
puntos altos y bajos, tendencias generales, agrupaciones y variaciones.
Examinar
simetría, dispersión y valores extremos.
Analizar los Patrones Visuales
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
¿Qué indican las frecuencias altas o bajas?
¿Existen tendencias o relaciones entre las variables?
Extraer Información Clave
¿Qué conclusiones se pueden inferir?
Unidad II: Distribución y frecuencia en C.S.
Lectura e interpretación de Gráficas
Relacionar la gráfica con el fenómeno social estudiado
Vincular los resultados con posibles causas o implicaciones prácticas.
Contextualizar
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
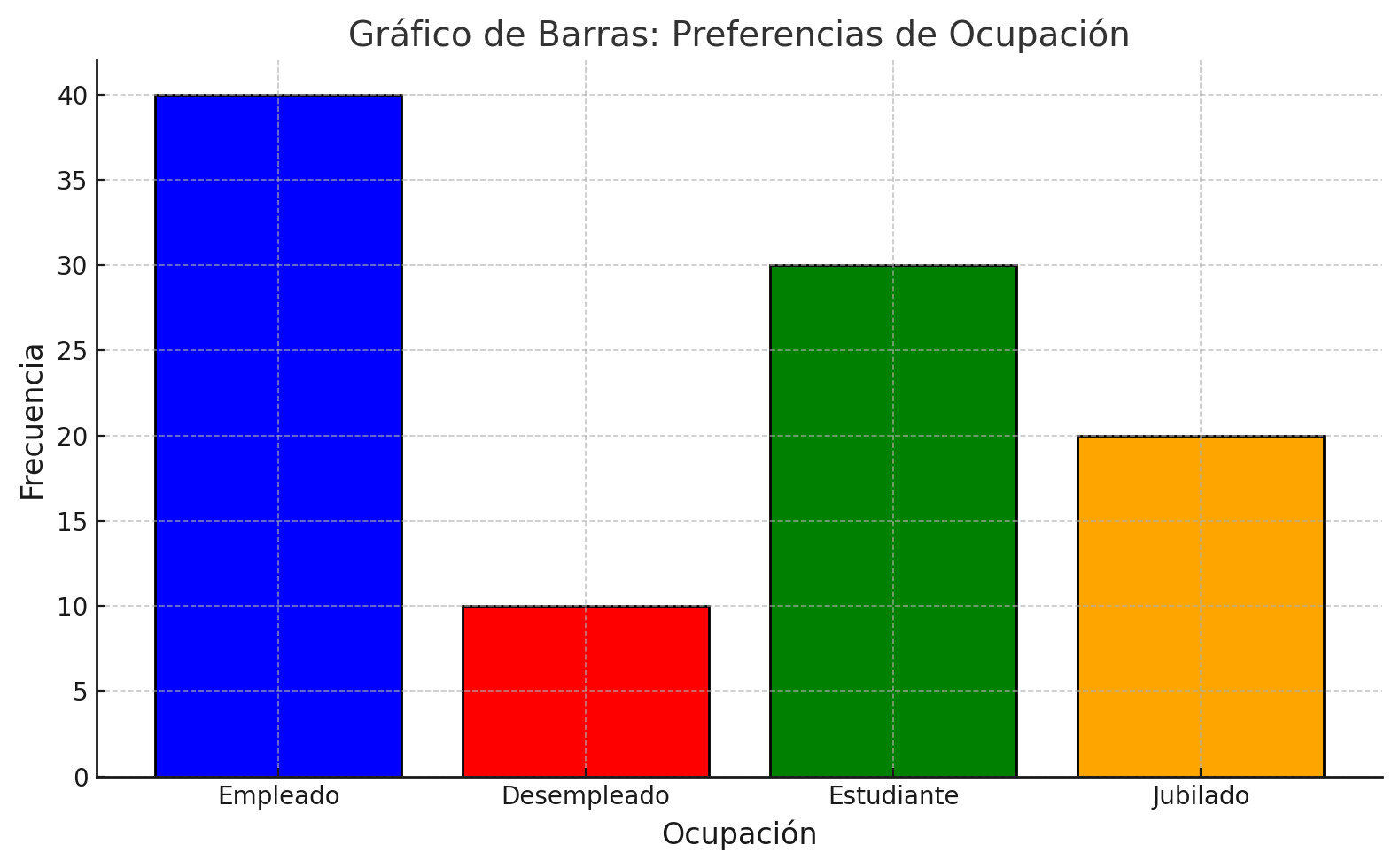
Unidad II: Distribución y frecuencia en C.S.
Actividad de aprendizaje
| Ocupación | Frecuencia |
|---|---|
Interpretación
- ?
- ?
- ?
Tabla 1. ? Fuente: ?

Unidad III
Las medidas de tendencia y su uso
Unidad III: Medidas de tendencias y usos
Las medidas de tendencia son herramientas estadísticas que permiten describir un conjunto de datos al identificar un valor central o representativo.
Unidad III: Medidas de tendecia y uso
Estas medidas resumen las características principales de los datos en un único valor, facilitando su interpretación y comparación.
Unidad III: Medidas de tendecia y uso
Resumir Datos
Ofrecen un valor representativo que facilita la comparación entre conjuntos de datos.
Identificar Patrones
Ayudan a detectar tendencias generales en un conjunto de datos, como el promedio de calificaciones en una clase.
Tomar Decisiones
Ayudan a detectar tendencias generales en un conjunto de datos, como el promedio de calificaciones en una clase.
Unidad III: Medidas de tendecia y uso
Describir Poblaciones
Permiten caracterizar grupos poblacionales, por ejemplo, determinando la edad promedio en una región.
Identificar Patrones
La relación entre estas medidas (media, mediana y moda) puede revelar la forma de la distribución de los datos, como si es simétrica o presenta sesgos.
Unidad III: Medidas de tendecia y uso (Actividad de Aprendizaje)

Unidad III: Medidas de tendecia y uso (media)
Comúnmente conocida como promedio, es una de las medidas de tendencia, más utilizadas en estadística.
Proporciona un valor representativo de un conjunto de datos, calculado al sumar todos los valores y dividir entre la cantidad total de datos.
Es una herramienta clave en el análisis estadístico, ya que permite interpretar y resumir grandes volúmenes de información de manera concisa.
Unidad III: Medidas de tendecia y uso (media)
La media es el valor que se obtiene al dividir la suma total de los datos por el número de observaciones.
Representa el equilibrio del conjunto de datos, es decir, si cada dato aportara un peso en una balanza, la media sería el punto donde se equilibra.
Unidad III: Medidas de tendecia y uso (media)
Fórmula de la Media
Para un conjunto de datos x1,x2,...,xnx_1, x_2, ..., x_nx1,x2,...,xn, la media se calcula como:
∑xi: Es la suma de todos los valores.
n: Es el número total de observaciones.
Unidad III: Medidas de tendecia y uso (media)
Tipos de Medias
Media Simple:
Se aplica cuando todos los datos tienen el mismo peso.
Unidad III: Medidas de tendecia y uso (media)
Tipos de Medias
Media Ponderada:
Se utiliza cuando los datos tienen pesos o frecuencias diferentes. La fórmula es:
wi son los pesos asociados a cada valor xix_ixi.
Unidad III: Medidas de tendecia y uso (media)
Tipos de Medias
Media Geométrica:
Utilizada para tasas de crecimiento o índices, calculada como:
Media Geomeˊtrica=x1⋅x2⋅...⋅xnn\text{Media Geométrica} = \sqrt[n]{x_1 \cdot x_2 \cdot ... \cdot x_n}
x1,x2,…,xn son los valores de la muestra.
∏i=1nxi es el producto de todos los valores.
Unidad III: Medidas de tendecia y uso (media)
Tipos de Medias
Media Armónica:
Empleada en datos relacionados con velocidades o ratios, calculada como:
x1,x2,…,xn son los valores de la muestra.
n es el número total de elementos.
Ventajas
Representa un conjunto de datos con un solo valor.
1
Fácil de calcular e interpretar.
2
Utilizable en datos cuantitativos continuos y discretos.
3
Unidad III: Medidas de tendecia y uso (media)
Desventajas
a valores extremos, un solo dato atípico puede alterar significativamente la media.
1
Sensibilidad
No siempre, en distribuciones sesgadas, la media puede no reflejar adecuadamente el centro de los datos.
2
Representativa
de detalle, al usar solo un valor, se pierde información sobre la dispersión de los datos.
3
Pérdida
Unidad III: Medidas de tendecia y uso (media)
Unidad III: Medidas de tendecia y uso (media)
Actividad de aprendizaje
Instrucciones: A continuación, se presenta un conjunto de datos sobre las calificaciones obtenidas por un grupo de estudiantes en un examen. Tu tarea es calcular la media aritmética de las calificaciones para determinar el promedio del grupo.
Datos: Las calificaciones obtenidas por 10 estudiantes son las siguientes:
85, 90, 78, 88, 92, 76, 84, 95, 89, 77.
Unidad III: Medidas de tendecia y uso (media)
Actividad de aprendizaje
Pasos para resolver:
- Sumar todas las calificaciones: Calcula la sumatoria de todos los valores.
- Contar el número de estudiantes: Determina la cantidad total de datos (nnn).
- Aplicar la fórmula de la media aritmética
Unidad III: Medidas de tendecia y uso (media)
Actividad de aprendizaje
- ¿Cuál es la media de las calificaciones del grupo?
- Si se añade una nueva calificación de 91, ¿cómo cambia el promedio?
Unidad III: Medidas de tendecia y uso (mediana)
Es una de las principales medidas de tendencia central en estadística.
Representa el valor que se encuentra en el centro de un conjunto de datos ordenados, dividiendo al grupo en dos partes iguales: el 50% de los valores están por debajo de la mediana y el otro 50% están por encima.
Unidad III: Medidas de tendecia y uso (mediana)
Es el valor central de un conjunto de datos cuando estos están ordenados de menor a mayor.
Si el número de datos es impar, la mediana será el valor que ocupa la posición central.
Si es par, la mediana se calcula como el promedio de los dos valores centrales.
Unidad III: Medidas de tendecia y uso (mediana)
Conjunto de datos impar (nnn es impar):
Donde x(k)x_{(k)}x(k) indica el valor en la posición kkk del conjunto ordenado.
Unidad III: Medidas de tendecia y uso (mediana)
Conjunto de datos par (nnn es par):
Es el promedio de los dos valores centrales.
Unidad III: Medidas de tendecia y uso (mediana)
usos
Robustez frente a valores atípicos
La mediana es menos sensible a valores extremos que la media, por lo que es útil en distribuciones sesgadas o con outliers.
Comparación entre grupos
Ayuda a identificar diferencias entre subconjuntos de datos al considerar únicamente el valor central.
Análisis de datos ordinales
La mediana es particularmente útil cuando los datos están en una escala ordinal (por ejemplo, niveles de satisfacción: muy bajo, bajo, medio).
Ventajas
Es fácil de calcular y entender
1
Representa el centro de los datos sin ser afectada por valores extremos.
2
Es adecuada para datos ordinales y distribuciones no simétricas.
3
Unidad III: Medidas de tendecia y uso (mediana)
Desventajas
No utiliza toda la información de los datos (solo se enfoca en el valor central).
1
Puede ser menos representativa en conjuntos de datos pequeños.
2
Unidad III: Medidas de tendecia y uso (mediana)
Unidad III: Medidas de tendecia y uso (mediana)
Ejemplo
Conjunto de Datos:
Calificaciones de 9 estudiantes en un examen:
72, 85, 88, 90, 91, 93, 95, 98, 100.
Ordenar los datos:
Ya están ordenados: 72,85,88,90,91,93,95,98,10072, 85, 88, 90, 91, 93, 95, 98, 10072,85,88,90,91,93,95,98,100.
Calcular la mediana
El número de datos es impar (n=9n = 9n=9), por lo que la mediana es el valor en la posición (9+1)/2 = 5 9+12=5\frac{9+1}{2} = 5
Mediana = 91
Unidad III: Medidas de tendecia y uso (mediana)
Ejemplo
Conjunto de Datos:
Calificaciones de 9 estudiantes en un examen: 72, 85, 88, 90, 91, 93, 95, 98, 100, 105.
Ordenar los datos:
Ya están ordenados: 72,85,88,90,91,93,95,98,10072, 85, 88, 90, 91, 93, 95, 98, 10072,85,88,90,91,93,95,98,100,105.
Calcular la mediana
El número de datos es par (n=10n = 10n=10), por lo que la mediana es el promedio de los valores en las posiciones 5 y 69+12=5\frac{9+1}{2} = 5
mediana = (91 + 93) / 2 = 92
Unidad III: Medidas de tendecia y uso (mediana)
Actividad de aprendizaje
Instrucciones: A continuación, se presenta un conjunto de datos que representan los ingresos mensuales (en dólares) de 15 familias en una comunidad. Ordena los datos, identifica la mediana y analiza su significado.
Unidad III: Medidas de tendecia y uso (mediana)
Actividad de aprendizaje
Datos de ingresos (sin ordenar):
2,400, 3,200, 2,800, 4,500, 3,600, 3,000, 2,700, 3,100, 4,000, 3,800, 2,600, 3,400, 4,200, 3,900, 4,100.
Unidad III: Medidas de tendecia y uso (mediana)
Actividad de aprendizaje
- Ordenar los datos de menor a mayor
- Identificar el número total de datos (nnn)
- Determinar la posición y calcular la mediana.
- Analizar el resultado
Unidad III: Medidas de tendecia y uso (moda)
La moda es una medida de tendencia central que representa el valor o los valores que ocurren con mayor frecuencia en un conjunto de datos.
Es especialmente útil cuando se desea identificar los valores más comunes en un conjunto de datos categóricos, ordinales o cuantitativos.
Unidad III: Medidas de tendecia y uso (moda)
El conjunto de datos tiene una única moda.
1
Unimodal
El conjunto de datos tiene dos valores con la misma frecuencia máxima
2
Bimodal
Hay tres o más valores con la misma frecuencia máxima.
3
Multimodal
Unidad III: Medidas de tendecia y uso (moda)
No hay moda, ya que todos los valores ocurren con la misma frecuencia.
4
Amodal
Unidad III: Medidas de tendecia y uso (moda)
Datos Categóricos
La moda es particularmente relevante para analizar datos cualitativos, como el color favorito, la marca preferida o la categoría de productos más vendida.
Datos Cuantitativos
En datos numéricos, la moda puede destacar valores recurrentes que son importantes para la toma de decisiones, como el tamaño de ropa más solicitado en una tienda.
Unidad III: Medidas de tendecia y uso (moda)
Aplicaciones
Identificar comportamientos comunes en estudios de mercado.
Analizar patrones en ciencias sociales, como la clase social más frecuente en una muestra poblacional.
Detectar valores recurrentes en registros médicos o educativos.
Unidad III: Medidas de tendecia y uso (moda)
Cálculo de la Moda en Datos Agrupados
- LLL: Límite inferior de la clase modal.
- fmf_mfm: Frecuencia de la clase modal.
- faf_{a}fa: Frecuencia de la clase anterior a la modal.
- fbf_{b}fb: Frecuencia de la clase posterior a la modal.
- hhh: Amplitud del intervalo.
Unidad III: Medidas de tendecia y uso (moda)
Ejemplo
Datos sin agrupar:
Calificaciones de 10 estudiantes: 85,90,75,90,80,85,90,95,80,9085, 90, 75, 90, 80, 85, 90, 95, 80, 9085,90,75,90,80,85,90,95,80,90.
Frecuencias:
- 909090: 4 veces.
- 858585: 2 veces.
- 808080: 2 veces.
- 75,9575, 9575,95: 1 vez cada uno.
Moda:
El valor con mayor frecuencia es 909090. Por lo tanto, la moda es 90.
Unidad III: Medidas de tendecia y uso (moda)
Ejemplo
| Intervalo de clase | Frecuencia (F) |
|---|---|
| 50−59 | 2 |
| 60−69 | 5 |
| 70−79 | 8 |
| 80−89 | 10 (clase modal) |
| 90−99 | 6 |
Unidad III: Medidas de tendecia y uso (moda)
Actividad de aprendizaje
Instrucciones:
Una tienda registró las tallas de zapatos más vendidas durante una semana. Los datos son los siguientes:
| Talla | Frecuencia |
|---|---|
| 35 | 3 |
| 36 | 5 |
| 37 | 8 |
| 38 | 10 |
| 39 | 7 |
| 40 | 4 |
- Identifica la moda a partir de los datos proporcionados.
- Interpreta el resultado en el contexto del problema.
- Si la frecuencia de la talla 39 aumenta a 10, ¿cómo cambiaría la moda?




Unidad IV
Los elementos de la Probabilidad
Unidad IV: Los elementos de la Probabilidad
Los conceptos básicos
Los tipos
Sucesos dependientes
Sucesos independientes
Sucesos excluyentes y no excluyentes
