Costly Belief Elicitation
| Brandon Williams |
Alistair Wilson |
| ASSA Beliefs Session January 2025 |


An experimental testbed for understanding effort and incentive in belief elicitation
Intro/ Basic Idea
- Experimental economists commonly give incentives when we elicit beliefs. Why?
- Hope that by providing incentives we collect better, more-accurate beliefs:
- Understanding what is asked requires effort
- Overcome personal motives to distort
- Doing burdensome calculations
- Therefore, if belief elicitation is an effortful exercise, how do we best increase the precision of the expressed belief?
Want to understand what incentives produce honest, deliberative beliefs
Motivation
0
100
20
80
Want to understand what incentives produce honest, deliberative beliefs
Motivation
0
100
20
80
Project Roadmap
- Create a task that mirrors forming a probabilistic belief that requires effort
- Use experiments on Prolific to understand the relationship between cost, effort, and output
- Vary the task primitives and measure how long it takes to complete (effort), willingness to accept (cost) and accuracy (output)
- Understand how hard this task is to guess (zero effort output)
- Then use the task with different incentives
- To do: Measure the psychological costs for forming objective Bayesian posteriors
Literature
Some examples of recent papers in belief elicitation:
-
Testing incentive compatibility:
- Danz, Vesterlund, and Wilson, 2022
- Healy and Kagel, 2023
-
"Close enough" payments:
- Enke, Graeber, Oprea, and Young, 2024
- Ba, Bohren, and Imas, 2024
- Settele, 2022
-
QSR or BSR:
- Hoffman and Burks, 2020
- Radzevick and Moore, 2010
- Harrison et al., 2022
-
Others (exact or quartile):
- Huffman, Raymond, and Shvets, 2022
- Bullock, Gerber, Hill, and Huber, 2015
- Prior, Sood, and Khanna, 2015
- Peterson and Iyengar, 2020
Treatments
So far we have the following treatments:
- A calibration treatment where we measure how long it takes to complete the problem (Effort); and how accurate you are (Output), then elicit your willingness to accept payment for the task (Cost)
- An initial guess treatment where we measure your first instinct (low-effort output)
- Incentives treatments where we change the reward structure (horserace across incentives)
Basic Task
- Create a task that mirrors forming a probabilistic belief that requires effort
- What is the proportion of blue tokens in this urn?

Ans: 56.25%
- Create a task that mirrors forming a probabilistic belief that requires effort
- Use experiments on Prolific to understand the relationship between cost, effort, and precision
- Vary the cost for precision and calibrate on how long it takes to complete and willingness to accept (calibration treatment)
- Understand how hard this problem is to guess (initial guess treatment)
- Vary the reward structure:
- BSR with no information
- BRR with qualitative information
- BSR with quantitative information
- A "close enough" incentive
Experimental task
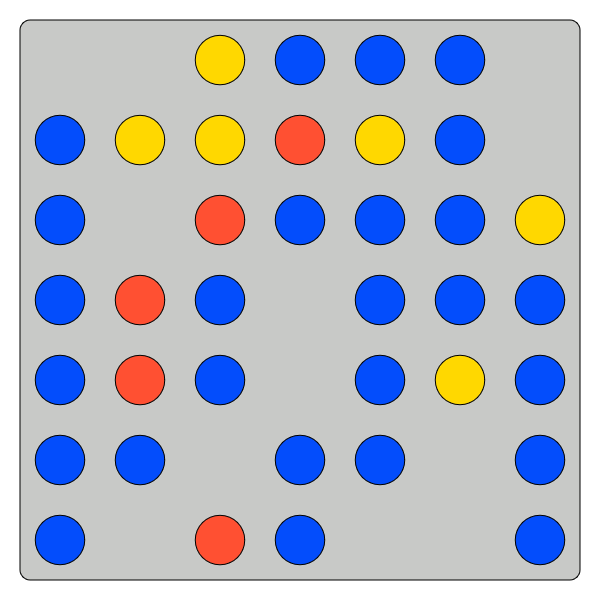
How to get you to exert effort when formulating your belief?
We start by paying $0.50 if you exactly count:
- Number of blue tokens
- Number of total tokens
Measure accuracy and time taken
Vary the difficulty over 5 tasks
Calibration: Training
Task Variance
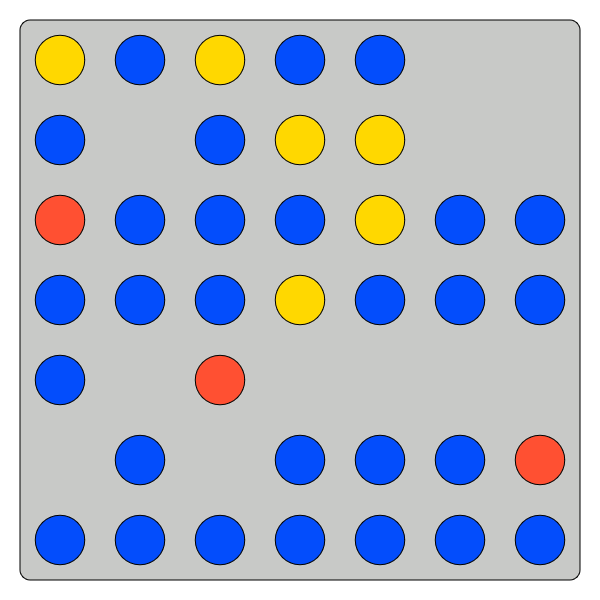



Small no gaps
Small gaps
Larger no gaps
Larger gaps
Task Variance

Each problem characterized by a tuple \(\left(N,\theta^\star,\delta_\text{Gaps}\right) \):
- \(N\): total number of tokens in urn
- \(\theta^\star\) the true proportion of blue tokens
- \(\delta_{\text{Gaps}}\): indicator for gaps
\(\left(N,\theta^\star,\delta_\text{Gaps}\right) = (139 , \tfrac{81}{139},1) \)
Willingness to Pay: Oprea (2020)
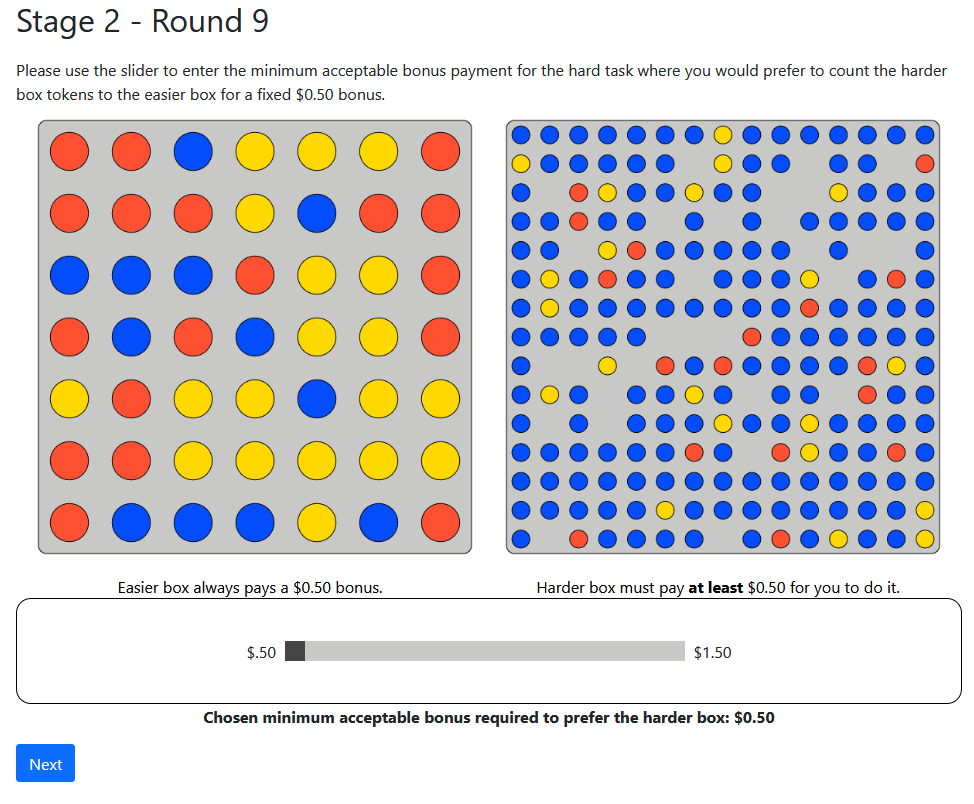
Ten rounds: An easy task, or a Hard one plus amount \(\$X\)
LHS:
Constant
Difficulty
RHS:
Varying
Difficulty
Always
Pays $.50
If Correct
$X
If Correct
Choose
$X threshold
Calibration Results (\(N=250\))
From models over \(\left(N,\log(N),\delta_\text{Gaps}\right) \)
Effort (time spent)
Cost (WTA)
Output (within 1%)
\(\text{OLS }\log(\text{Effort})\)
\(\text{Tobit}(\text{WTA})\)
\(\text{Logit}(\text{Within 1\%})\)
Initial Guesses
Need to get a sense for how hard this problem is to guess.
- Give them 15 or 45 seconds to form and enter a guess on the proportion
- Higher powered rewards:
- $2.50 if within 1%
- $1.00 if within 5%
- $0.50 if within 10%
- Ask them about 10 proportions (pay three decisions)
Initial Guess Results (\(N=200\))
After 15 second
After 45 second
Task Conclusions
- So we have an experimental task that:
- We can scale the difficulty
- Where we understand the broad costs and efforts required to succeed
- Where we understand the output level at low-effort
Incentives
Use four incentives to ask about beliefs in ten different urns:
-
BSR-Desc: $1.50 prizewith only qualitative information on the details
- Text description of payoff structure (Vespa & Wilson, 2018)
-
BSR-Inf: as above but with quantitative information
- Full information on the quantitative incentives (Danz et al., 2022)
- BSR-NoInf: only know there is a $1.50 prize, no other information on the incentives
- A "close enough" incentive
- $1.50 if within 1%; $0.50 if within 5%
- Current use in several papers (e.g. Ba et al., 2024)
- Pay three of the rounds
- \(N=100\) each incentive treatment
- No time limit
Model
- Agents know that there are \(N\) tokens in the urn, but are unsure about the blue proportion
- Initial prior on the number of blue tokens is \[\text{BetaBinomial}(1,1,N)\]
- Can choose to sample \(0 \leq n \leq N \) tokens without replacement from the urn (Hyper geometric signal)
- Counting \(k\) blue balls and \(n-k\) non-blue leads to posterior \[\text{BetaBinomial}(1+k,1+n-k,N-n)\]
- With this model we can calculate the expected return from counting \(n\) balls from \(N\) under a mechanism that incentivizes a report \(q\) with payment \(\phi(q)\)
Incentives to Exert Effort
Results
Output by difficulty
Using our calibration treatments to construct instruments for difficulty:
Effort by difficulty
Using our calibration treatments to construct instruments for difficulty:
Output: Accuracy
-15%
+16%
+56%
+43%
Effort compared to Calibration

Aside: Cognitive Uncertainty
Common self-reported measure, which here we validate against effort and output in BSR-NoInf treatment...
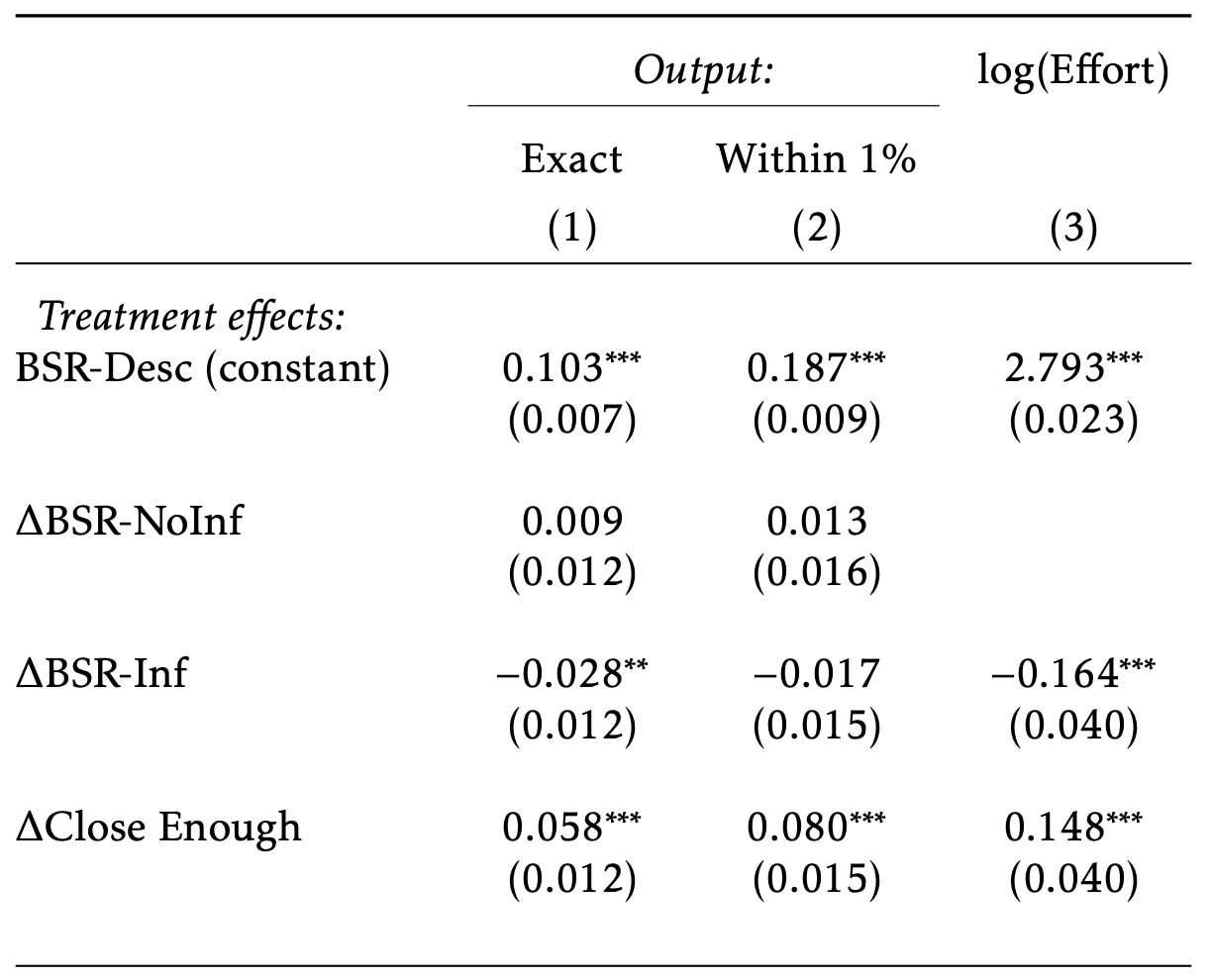
Incentive effects
- "Close enough" outperforms BSR on both accuracy and time spent
- The better incentive effects stemming from a richer outcome space
- Also cheaper for the experimenter, payments to participants reduced by ~50% over BSR
- With a fixed budget, how much more effort could be induced?
- (But the gains here are dwarfed by the gains when we explicitly tell them what to do)
Incentive effects
Conclusions (so far...)
- Have a well-behaved task, which scales in cost/effort/output
- Close enough incentive works best well for inducing effort
- Varying the incentives:
- For BSR, no substantive differences
- Close enough produces substantial increase in effort/output; mirrors the theoretical predictions
- Still, offering incentives and letting them choose effort is swamped by authority of telling them what to do
To do:
- Examine and measure the effective costs for Bayesian updating elicitations in experiments
Bayesian Updating
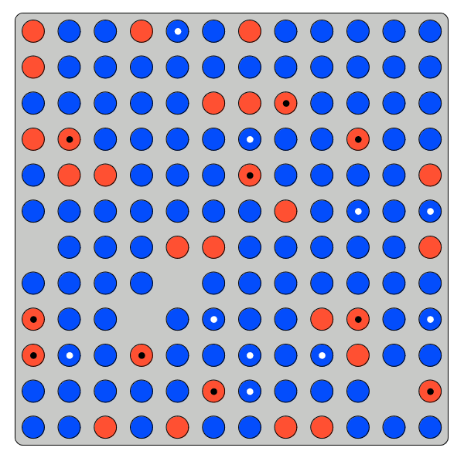
Participants told:
- Number of tokens
- Proportion blue
- Proportion Dots | Blue
- Proportion Dots | Red
Are then asked for the proportion of blue balls given a dot:
- Calculation identical to standard Bayesian updating experiments
- But can also just count...
After gaining experience will ask WTP against standard counting task