No one in the brief history of computing has ever written a piece of perfect software. It's unlikely that you'll be the first
Andy Hunt
Programming Safely With types
Ian Thomas | @anatomic
Does JavaScript Have Types?
(And can they be safe?)
JavaScript's Types
- Undefined
- Null
- Boolean
- String
- Number
- Object
- Symbol
What is safety?
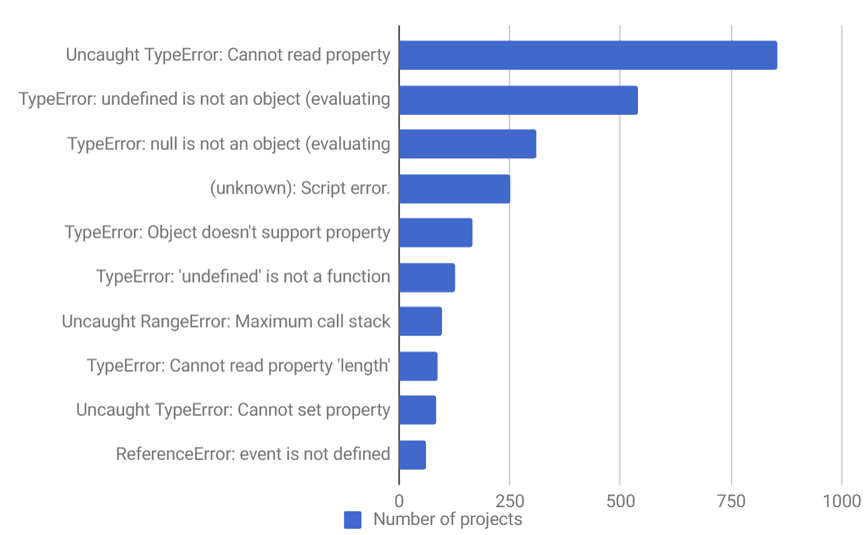
What are the most frequently reported errors in JavaScript applications?
In computer science, type safety is the extent to which a programming language discourages or prevents type errors.
Wikipedia
The behaviours classified as type errors [..] are usually those that result from attempts to perform operations on values that are not of the appropriate data type
Wikipedia
Static vs Dynamic; Strong vs weak
Spot the difference
const a = null;
a.prop; // #1
const b = undefined;
b.prop; // #2What happens at 1 and 2?
- 💥 TypeError: Cannot read property 'prop' of null 💥
- Silently fails, returns undefined
Which is Interesting because...
> typeof null
'object'🙈
Getting the first item from an array
What should we return...
- When the input is an array of > 0 items?
- When the input is an empty array?
- When the input is not an array?
the happy path is obvious, but what about the failure branch(es)?
Null, undefined or false?
accessing data nested in objects
const a = { a: { b: { c: [1, 2, 3] } } };
const b = { a: { b: { c: undefined } } };
const sumC = data => {
// what goes in here?
};const a = { a: { b: { c: [1, 2, 3] } } };
const b = { a: { b: { c: undefined } } };
const add = (a, b) => a + b;
const sumC = data => data.a.b.c.reduce(add, 0);
sumC(a); // 6
sumC(b); // ?A naive approach
TypeError: Cannot read property 'reduce' of null
How can we improve this code?
const a = { a: { b: { c: [1, 2, 3] } } };
const b = { a: { b: { c: undefined } } };
const add = (a, b) => a + b;
const sumC = data => {
if (data.a.b.c && Array.isArray(data.a.b.c)) {
return data.a.b.c.reduce(add, 0);
}
// What do we return here?
}Add a guard clause
How do we represent the failure branch in this function?
// Option 1
return false;// Option 2
return null;// Option 3
throw new Error("An array is required to sum");// Option 4
throw new CannotSumError("C should be an array");😬
If we are regularly accessing nested properties, how can we formalise this approach and make it reusable?
There has to be a better way!?
pure functions
Consistent return types
immutable data structures
introducing
ADTS
The data types provided in Crocks allow you to remove large swaths of imperative boilerplate, allowing you to think of your code in terms of what it does and not how it does it.
Crocks
Sum types to the rescue
First, a quick intro to haskell-like type signatures
data Bool = True | False
User defined types
type EventId = Int
Type aliases / Synonyms
add :: Int -> Int -> Int
Function signatures
Introducing Maybe
data Maybe a = Just a | Nothing
Maybe is well suited for capturing disjunction when the cause of the "error" case does not need to be communicated. For example, providing default values on specific conditions.
const a = { a: { b: { c: [1, 2, 3] } } };
const b = { a: { b: { c: undefined } } };
const add = (a, b) => a + b;
const sumC = data => {
if (data.a.b.c && Array.isArray(data.a.b.c)) {
return Just(data.a.b.c.reduce(add, 0));
}
return Nothing();
}A solution using ADTs
const prop = require("crocks/Maybe/prop");
const propPath = require("crocks/Maybe/propPath");
const data = { a: { b: { c: [1, 1, 2, 3, 5] } } };
const a = prop("a", data); // Just { b: { c: [1, 1, 2, 3, 5] } }
const b = prop("b", data); // Nothing
const c = propPath(["a", "b", "c"], data); // Just [1, 1, 2, 3, 5]
const d = propPath(["a", "b", "d"], data); // Nothingsafely getting properties from objects
This is great, but how do we work with the value inside a Maybe?
Maybe is a Functor
A value which has a functor must provide a map method. The map method takes one argument
map :: Functor f => f a ~> (a -> b) -> f bJust.prototype.map = function(fn) { return Just(fn(this.value)) };
What happens When You Get a nothing?
Nothing.prototype.map = function(fn) { return this; };const a = { a: { b: { c: [1, 2, 3] } } };
const b = { a: { b: { c: undefined } } };
const sumC = data =>
propPath(["a", "b", "c"], data)
.map(vals => vals.reduce(add, 0));
sumC(a); // Just 6
sumC(b); // NothingWe can re-write our solution using the new helper functions
Currying, Composition and Point-free style
propPath :: Foldable f => f (String | Integer) -> a -> Maybe bCurrying, Composition and point-free style
Arrows indicate currying
Value is only returned when all other arguments are provided
"f" has to be an ADT which implements the foldable typeclass (i.e. an array or List)
propPath :: Foldable f => f (String | Integer) -> a -> Maybe b
map :: (a -> b) -> m a -> m b
reduce :: (b -> a -> b) -> b -> m a -> b
compose :: ((y -> z), ..., (a -> b)) -> a -> z
pipe :: ((a -> b), ..., (y -> z)) -> a -> z
Currying, Composition and point-free style
// getC :: a -> Maybe b
const getC = propPath(["a", "b", "c"]);
// sum :: Foldable f => f Number -> Number
const sum = reduce(add, 0);
// sumC :: a -> Maybe Number
const sumC = pipe(getC, map(sum));Currying, Composition and point-free style
const sum = reduce(add, 0);Taking a closer look at our reduction
"empty" value (aka identity)
Combines two values together (aka concat)
We could use a monoid
any ADT that provides both an empty and a concat function can be used as a Monoid
Each Monoid provides a means to represent a binary operation and is usually locked down to a specific type. These are great when you need to combine a list of values down to one value.
// Instead of this
const add = (a, b) => a + b;
const sum1 = reduce(add, 0);
// We can use the built in behaviours of the Sum Monoid
const sum2 = mreduce(Sum);Using a Monoid
💡Note that sum1 and sum2 are equivalent - both take an array of numbers and return a number
// sumC :: a -> Maybe Number
const sumC = pipe(
propPath(["a", "b", "c"]),
map(mreduce(Sum));Our final implementation
Our program has been completely built from generic, reusable library code
mreduce vs mconcat vs mreduceMap vs mconcatMap
mconcat :: Monoid m, Foldable f => m -> f a -> m a
mconcatMap :: Monoid m, Foldable f => m -> (b -> a) -> f b -> m a
mreduce :: Monoid m, Foldable f => m -> f a -> a
mreduceMap :: Monoid m, Foldable f => m -> (b -> a) -> f b -> amreduce vs mconcat vs mreduceMap vs mconcatMap
Getting the first item from an array
Jumping back...
// head :: Foldable f => f a -> Maybe a
const head = xs => (Array.isArray(xs) && xs.length > 0 ? Just(xs[0]) : Nothing();)Getting the first item from an array
// head :: Foldable f => f a -> Maybe a
function head(xs) {
if (Array.isArray(xs) && xs.length > 0) {
return Just(xs[0]);
}
return Nothing();
}
What if we need to represent more than
Nothing?
Maybe
is just the start of this adventure...
data Either e a = Left e | Right a
data Result e a = Err e | Ok a
data Async e a = Rejected e | Resolved a
data RemoteData e a = NotAsked | Loading | Error e | Success a
type Pair a b = (a, b)
This all sounds great, but why the crazy names!?
The specifications in this list do not derive from goals such as trying to write rules for lists and maps. Instead, they start by noticing rules that apply in common to disparate structures.
Aside, Why Fantasy Land?
Yeah this is really not happening. It totally ignores reality in favor of typed-language fantasy land, making a more awkward and less useful API just to satisfy some peoples' aesthetic preferences that aren't even applicable to JavaScript.