Structure and dynamics of electron-phonon coupled systems using neural quantum states
Ankit Mahajan
Reichman Group, Columbia University

AM, Robinson, Lee, Reichman arXiv:2405.08701
Introduction




Many-body quantum effects:
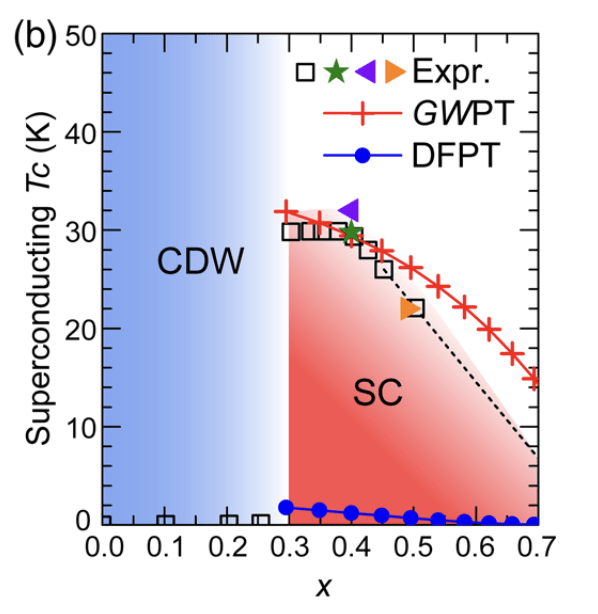
Riley, et al. Nature Communications 9(1), 2305 (2018)
Li, et al. PRL 122, 186402 (2019)
Electron-lattice interaction using linear approximation
Lattice energy within harmonic approximation


Outline
- Models, wave functions, and methods
- Ground state properties
- Excited states and dynamical properties
Model Hamiltonians
Using a Bloch basis
General linear coupling
Local lattice Hamiltonians (in the site basis)
- Holstein: density coupling

electron coupling to intramolecular vibrations in molecular crystals
Model Hamiltonians
- SSH / Peierls: phonon modulated hopping
- Bond model: phonons on bonds
Fillings:
- Dilute limit: polaron and bipolaron effects, relevant in lightly doped or photoexcited carriers in semiconducting systems
- Dense limit: interplay of e-e and eph interactions
Outline
- Model Hamiltonians
- NQS and variational Monte Carlo (VMC)
- Results
- Calculation of dynamical correlation functions
- Results
- Ground state properties
- Excited states and dynamical properties
Neural quantum states

Occupation numbers as inputs to a fully-connected feedforward network
Symmetry projection (site basis): drastically improves performance
For dense systems, we use a GHF reference:
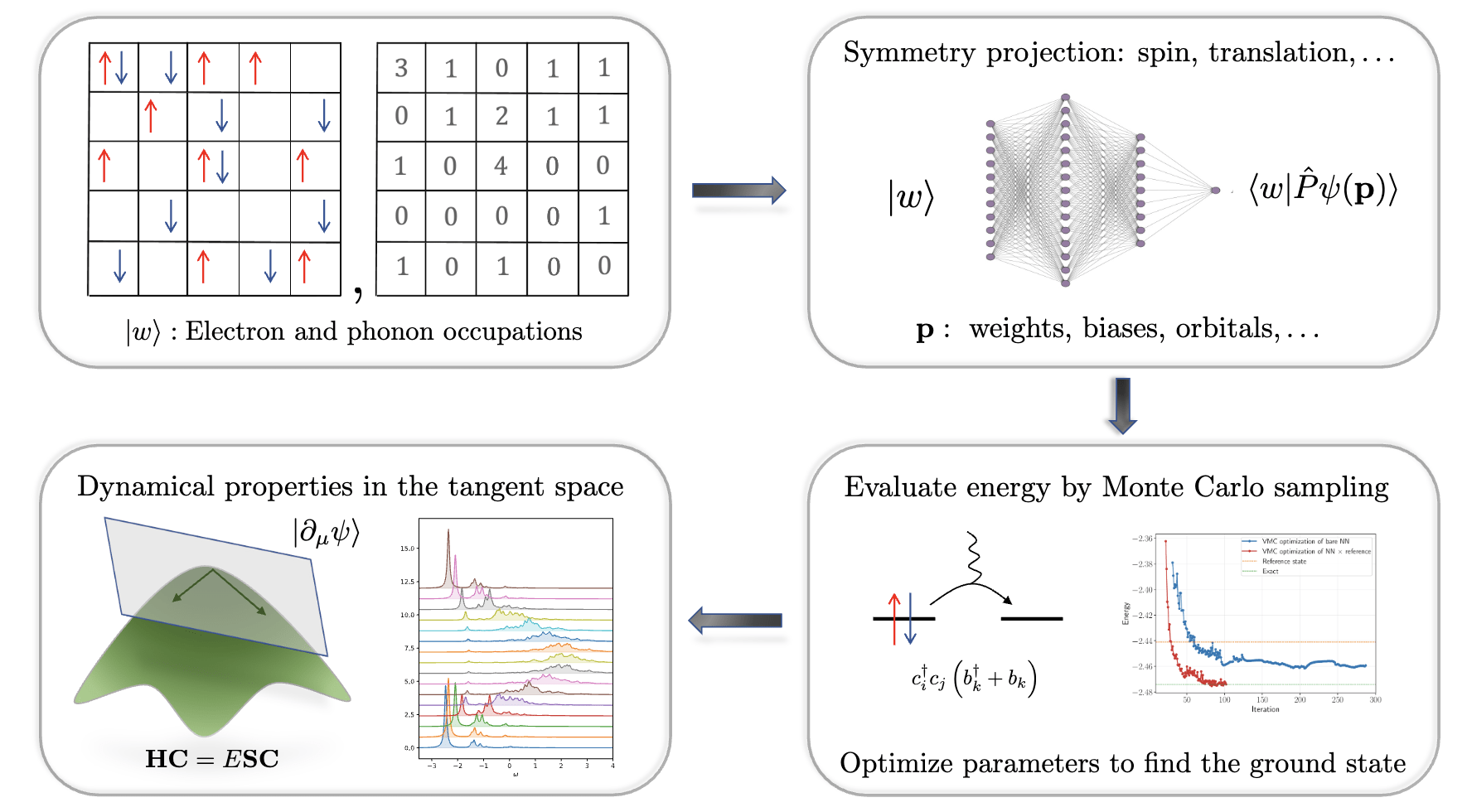
Neural quantum states
For dense systems, we use a GHF reference:
Symmetry projection: drastically improves performance

With translational symmetry, polaron NQS with one hidden neuron is equivalent to the Toyozawa wave function
e-e and e-ph Jastrows can also be efficiently represented using NQS
Variational Monte Carlo:
For polarons and bipolarons, cost of energy calculation with translational symmetry ~ cost in the momentum basis
Rejection free sampling, AMSGrad optimization
Outline
- Model Hamiltonians
- NQS and variational Monte Carlo (VMC)
- Results
- Calculation of dynamical correlation functions
- Results
- Ground state properties
- Excited states and dynamical properties

30 site chain, \(\omega_0=0.5\)
Holstein
Bond
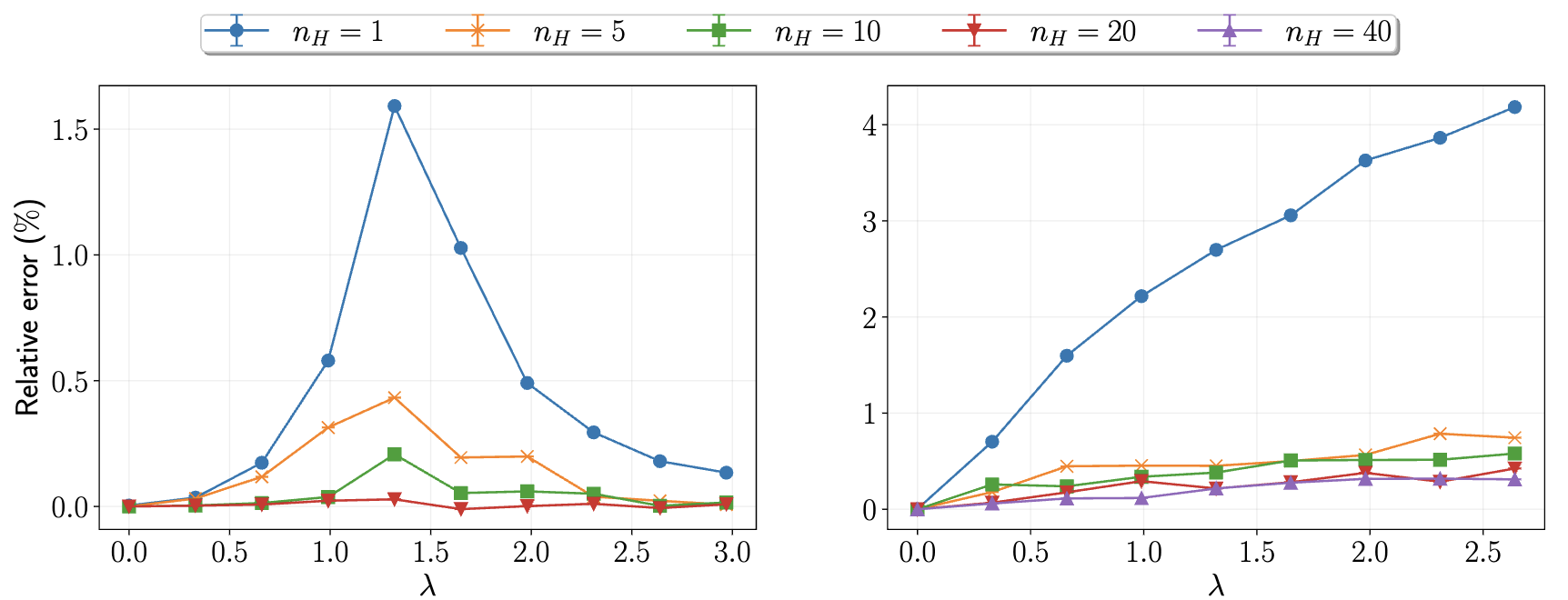
10x10 square lattice
Convergence of polaron binding energy with the number of hidden neurons
DQMC: Zhang, et al. Physical Review B (2021)

Electron-phonon correlation function
10x10 square lattice, \(\omega_0=1, \lambda=0.5\)


Dispersive phonons and avoided crossings
42 sites Holstein* polaron with \(\omega_q=1+0.8\cos(q)\), \(\lambda=0.5\)
Model from: Bonča and Trugman Physical Review B (2021)
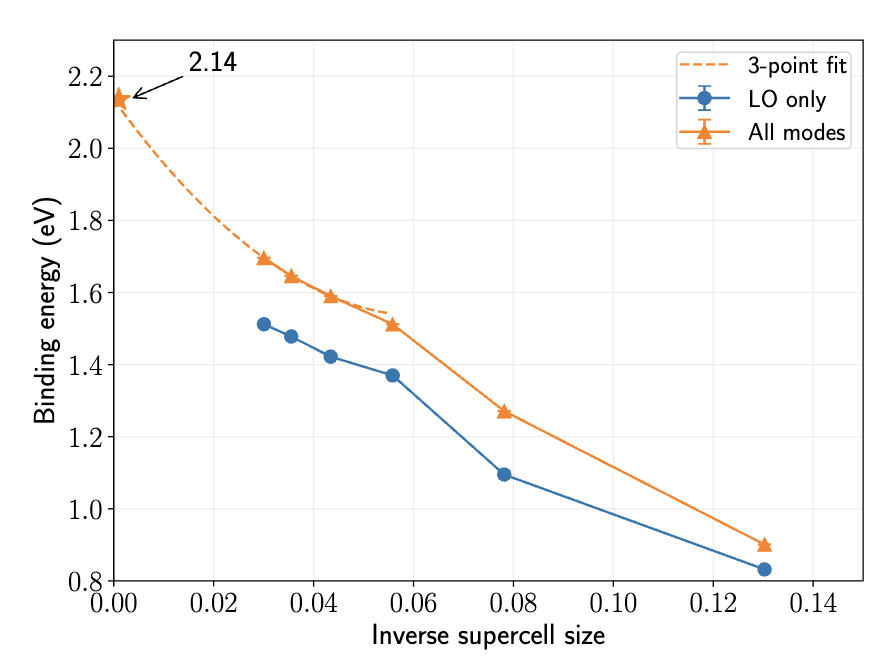
Lithium fluoride hole polaron
Ab initio model with 3 e and 6 \(\nu\) bands
Other estimates: 1.98 eV (DFPT), 2.2 eV (GFPT), 1.96 eV (CSPT2)
13x13x13


Bipolarons: 12x12 lattice, light and strongly bound
Bond
SSH
Half-filled, 20 site chain, \(\omega_0=1, U=4\)
AF \(\rightarrow\) CDW
AFQMC: Lee, et al. Physical Review B (2021)
Outline
- Model Hamiltonians
- NQS and variational Monte Carlo (VMC)
- Results
- Calculation of dynamical correlation functions
- Results
- Ground state properties
- Excited states and dynamical properties
LR-VMC: excited states and dynamic properties


Calculation of \(\langle w|H|\psi_{\nu}\rangle\) for all \(\nu\) can be performed at the same cost as energy by using reverse mode AD!
Tangent space of the NQS ansatz provides a natural subspace for describing low-lying excitations
Using ground state probability for sampling is very inefficient.

Reweighting technique

Sample from a distribution that has significant support on excited states
Holstein polaron: \(\omega_0=1\), \(\lambda=1\), 6 sites, 5 maximum phonons
Outline
- Model Hamiltonians
- NQS and variational Monte Carlo (VMC)
- Results
- Calculation of dynamical correlation functions
- Results
- Ground state properties
- Excited states and dynamical properties
Convergence of the one particle spectral function
Bond polaron: 8 sites, \(\omega_0=1\), \(\lambda=1\), \(\eta=0.05\)



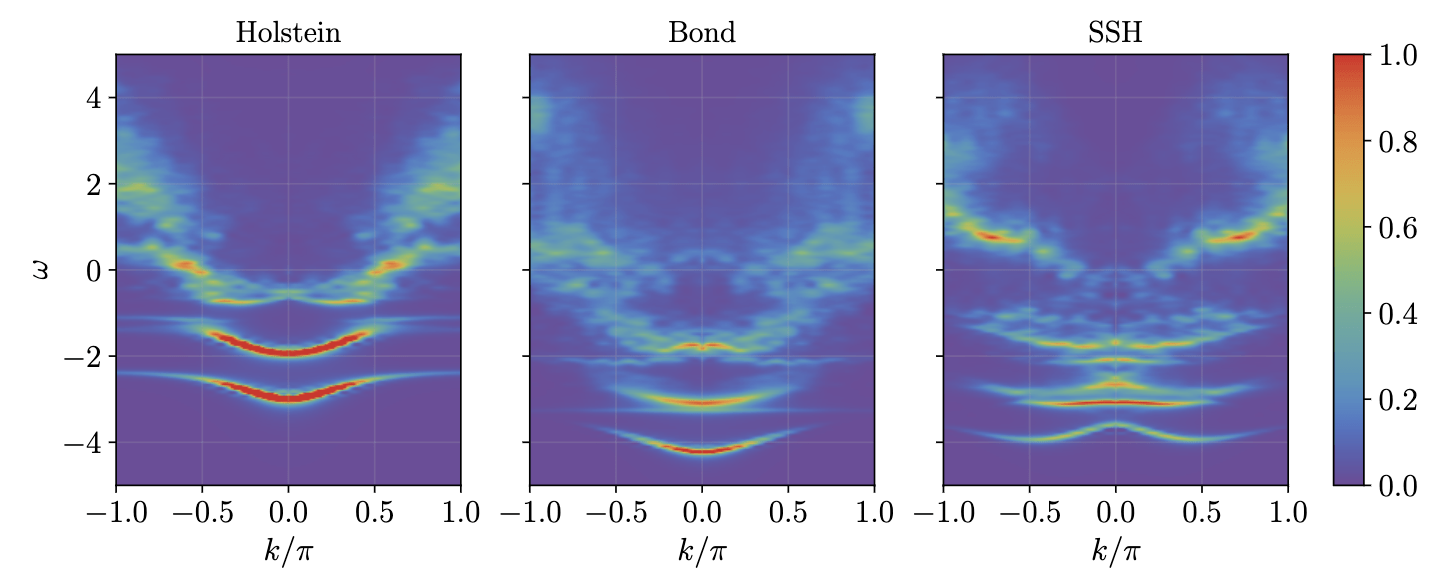
LR-VMC polaron spectral functions on a 30 site chain, \(\omega_0=1\), \(\lambda=1\)
Hubbard-Holstein model
Dynamical spin and charge structure factors for a half-filled 30 site chain, \(\omega_0=5, \lambda=0.25\), and \(U=4\)

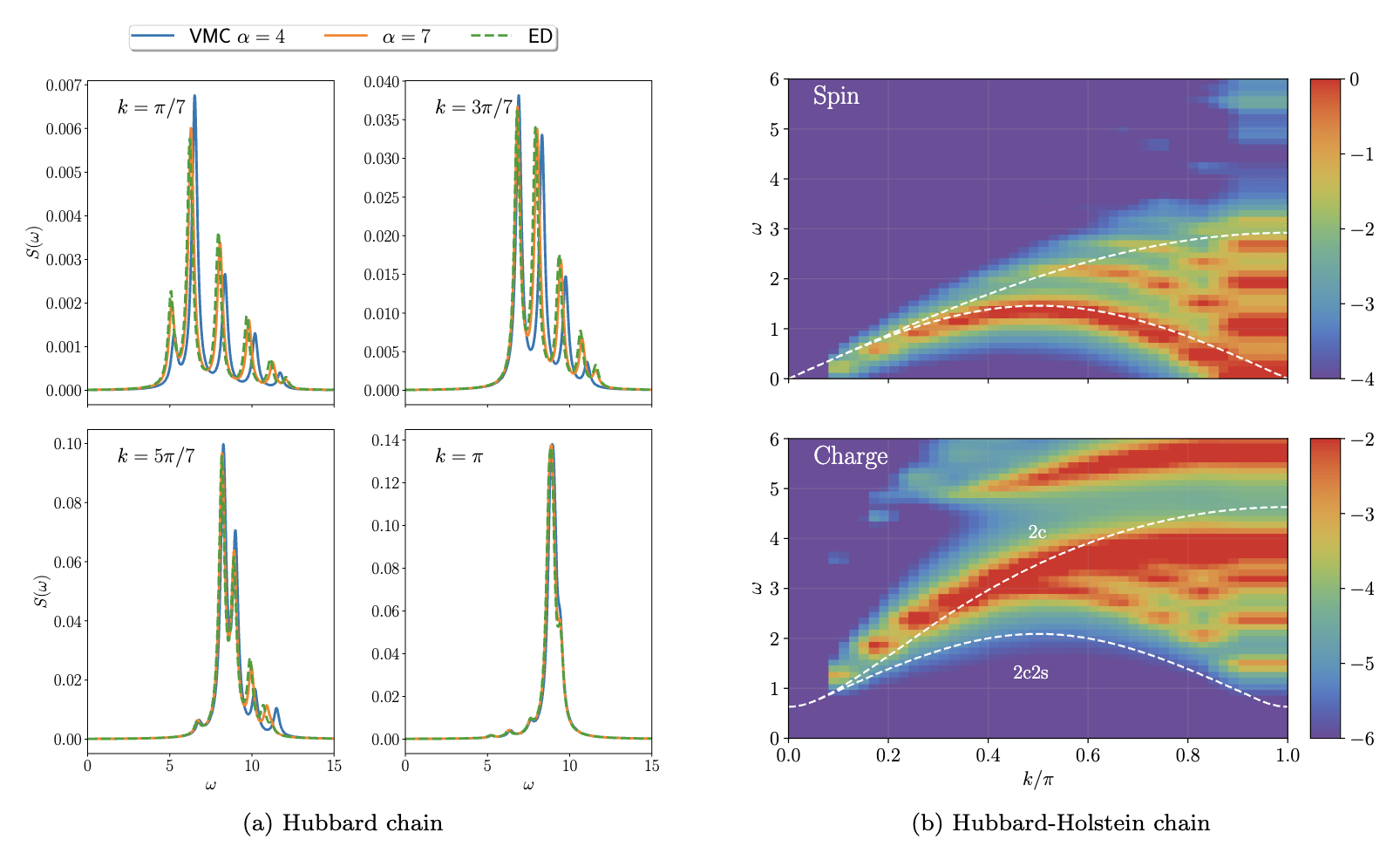
Summary
- NQS can be used to describe a range of eph interactions accurately and efficiently
- This method can be used to perform ab initio calculations with non-trivial systems
- It allows the calculation of dynamical properties as a natural extension of the ground state method
- Future work will focus on finite temperature properties and better description of electron correlation within NQS