Correlations and symmetry in mean-field wavefunctions

Molecular orbital theory

Valence bond theory

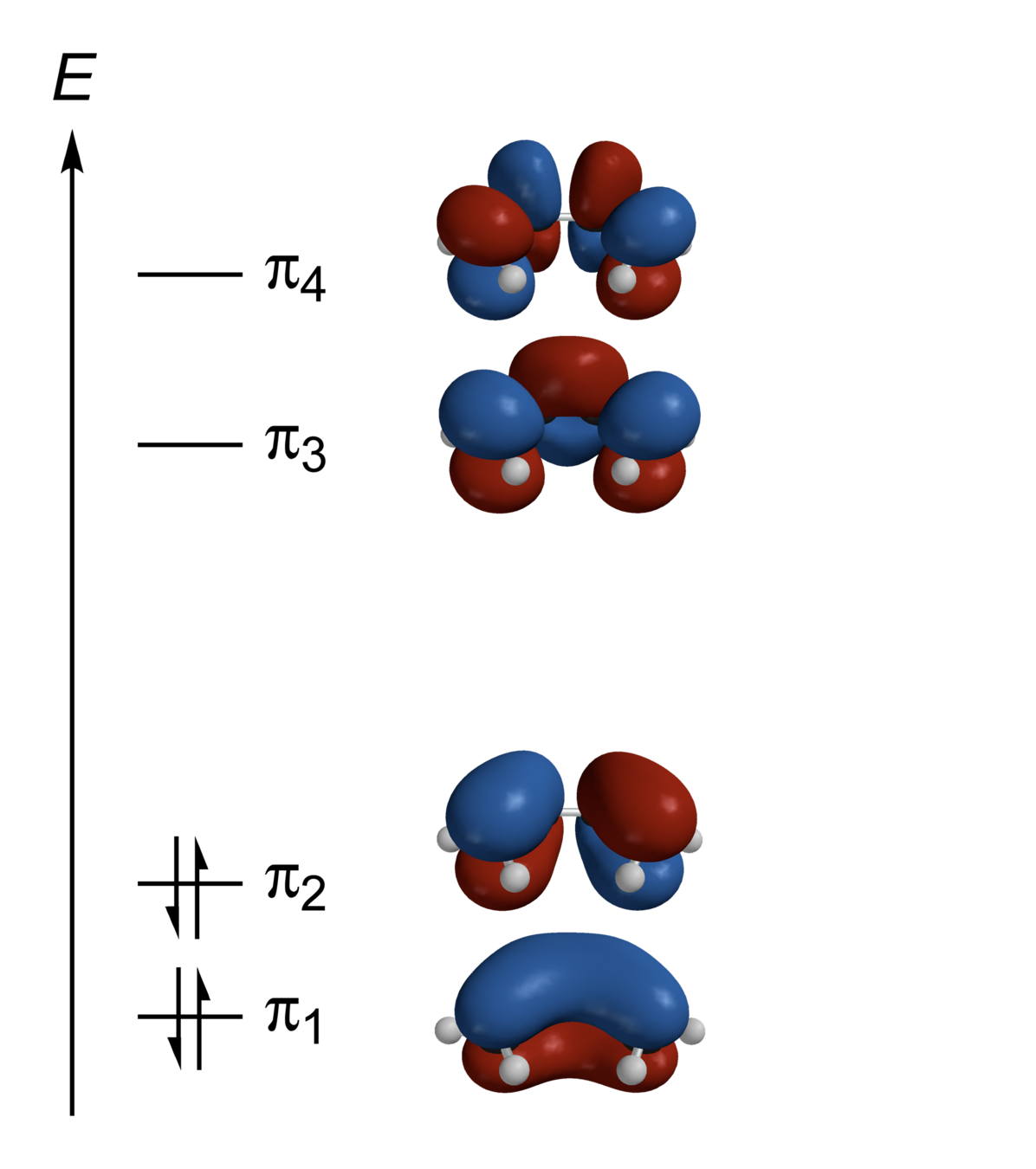
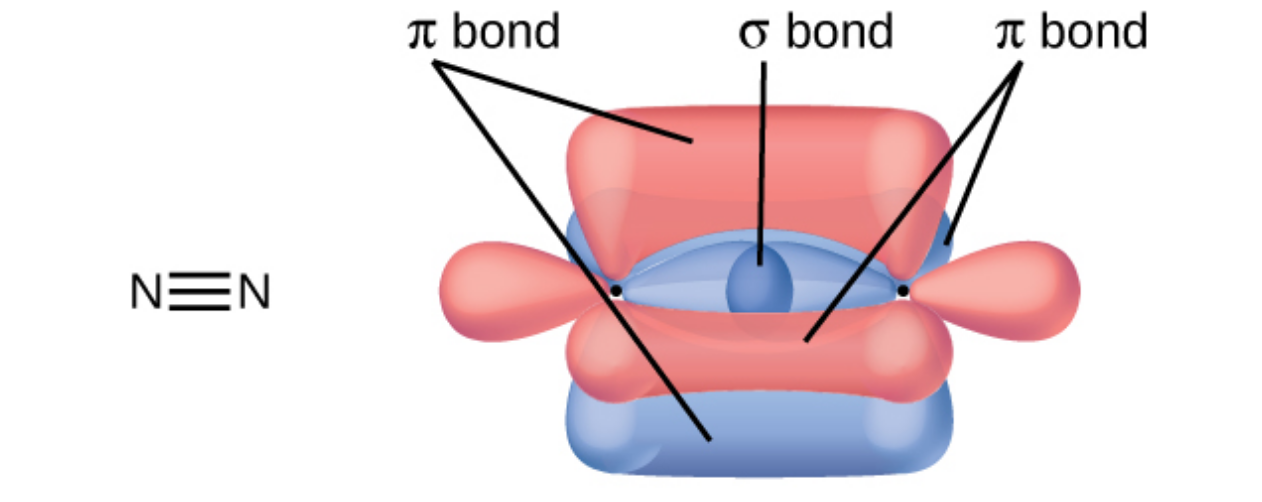
Variational principle

E = \dfrac{\langle \psi|H|\psi\rangle }{\langle \psi|\psi\rangle}

Strategy:

Ground state minimizes

  • Come up with a clever wavefunction parametrization
  • Minimize its energy by varying parameters (we use Monte Carlo methods to do this)

Variational Monte Carlo

\ \dfrac{\langle \psi(\mathbf{p})|H|\psi(\mathbf{p})\rangle }{\langle \psi(\mathbf{p})|\psi(\mathbf{p})\rangle} = \sum_{\mathbf{n}} \rho_{\mathbf{n}} E_L[\mathbf{n}]
  • Calculate energy: continuous time sampling
E_L[\mathbf{n}] = \sum_{\mathbf{m}} H_{\mathbf{n},\mathbf{m}} \frac{ \langle \mathbf{m}|\Psi(\mathbf{p})\rangle}{\langle \mathbf{n}|\Psi(\mathbf{p})\rangle}

overlap ratios

  • Calculate energy gradient: by sampling
|\mathbf{n}\rangle =

 local orbitals allow screening of distant excitations

\frac{\partial E(\mathbf{p})}{\partial\mathbf{p}}
  • Change parameters: smart gradient descent

walker

\epsilon
  • \( O(N^3) \) scaling, parallelizable

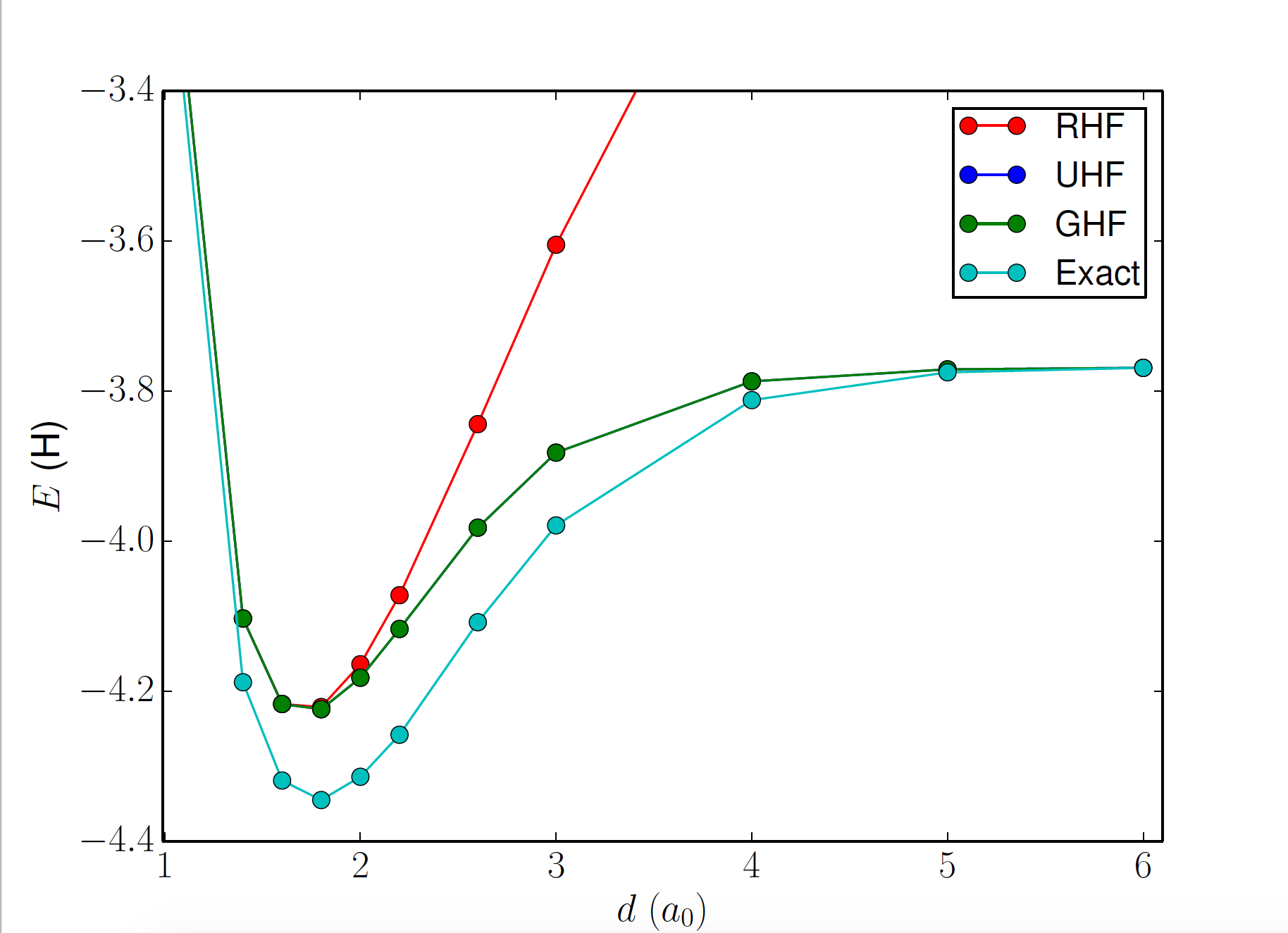
Restricted Hartree Fock (RHF)

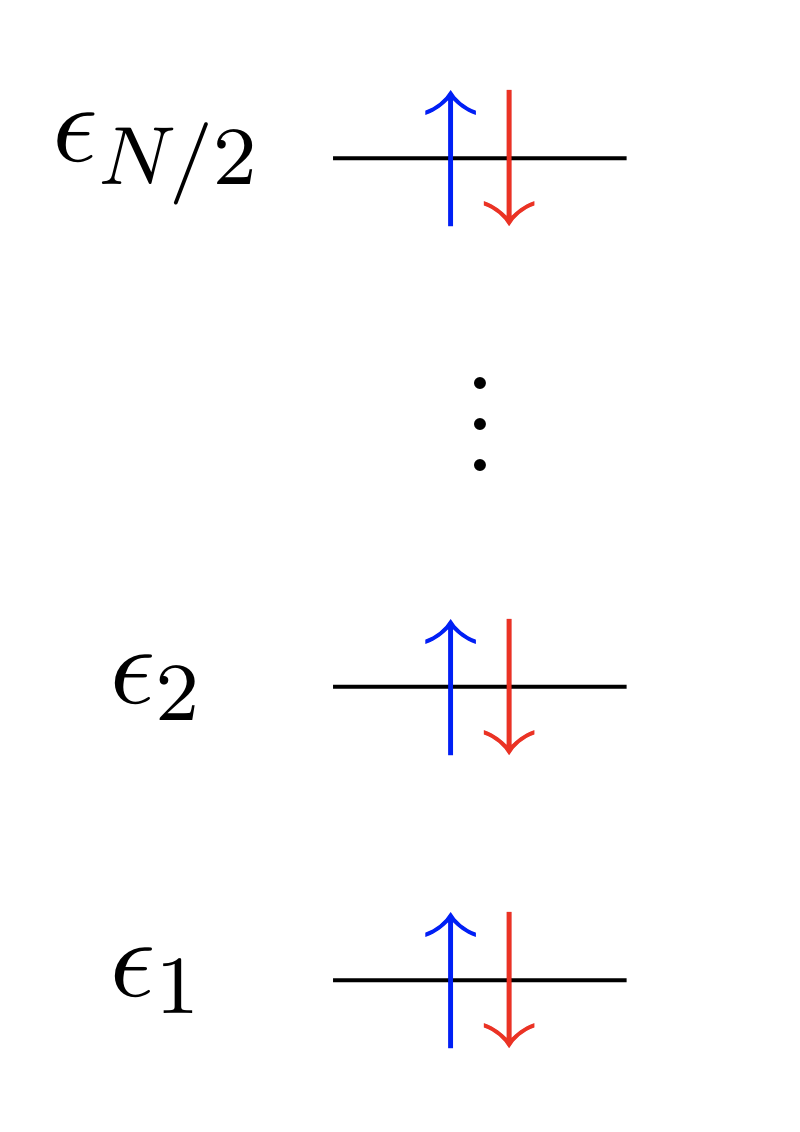
Doubly occupied orbitals:

|\psi\rangle = c_{1\uparrow}^{\dagger}c_{1\downarrow}^{\dagger}c_{2\uparrow}^{\dagger}c_{2\downarrow}^{\dagger}\dots c_{\frac{N}{2}\uparrow}^{\dagger}c_{\frac{N}{2}\downarrow}^{\dagger}|0\rangle
c_{i\sigma}^{\dagger}=\sum_{l}\theta^{l}_{i}a^{\dagger}_{l\sigma}
local

atomic

molecular

\langle\mathbf{n}|\psi\rangle = \text{det}(\qquad)\text{det}(\qquad)

\(\theta\) slices

\psi=\mathcal{A}[\phi_1(r_{1\uparrow})\phi_1(r_{1\downarrow})\dots \phi_{N/2}(r_{N/2\uparrow})\phi_{N/2}(r_{N/2\downarrow})]

Shortcomings of restricted orbitals

  • Doesn't correlate \(\uparrow\) and \(\downarrow\) electrons 
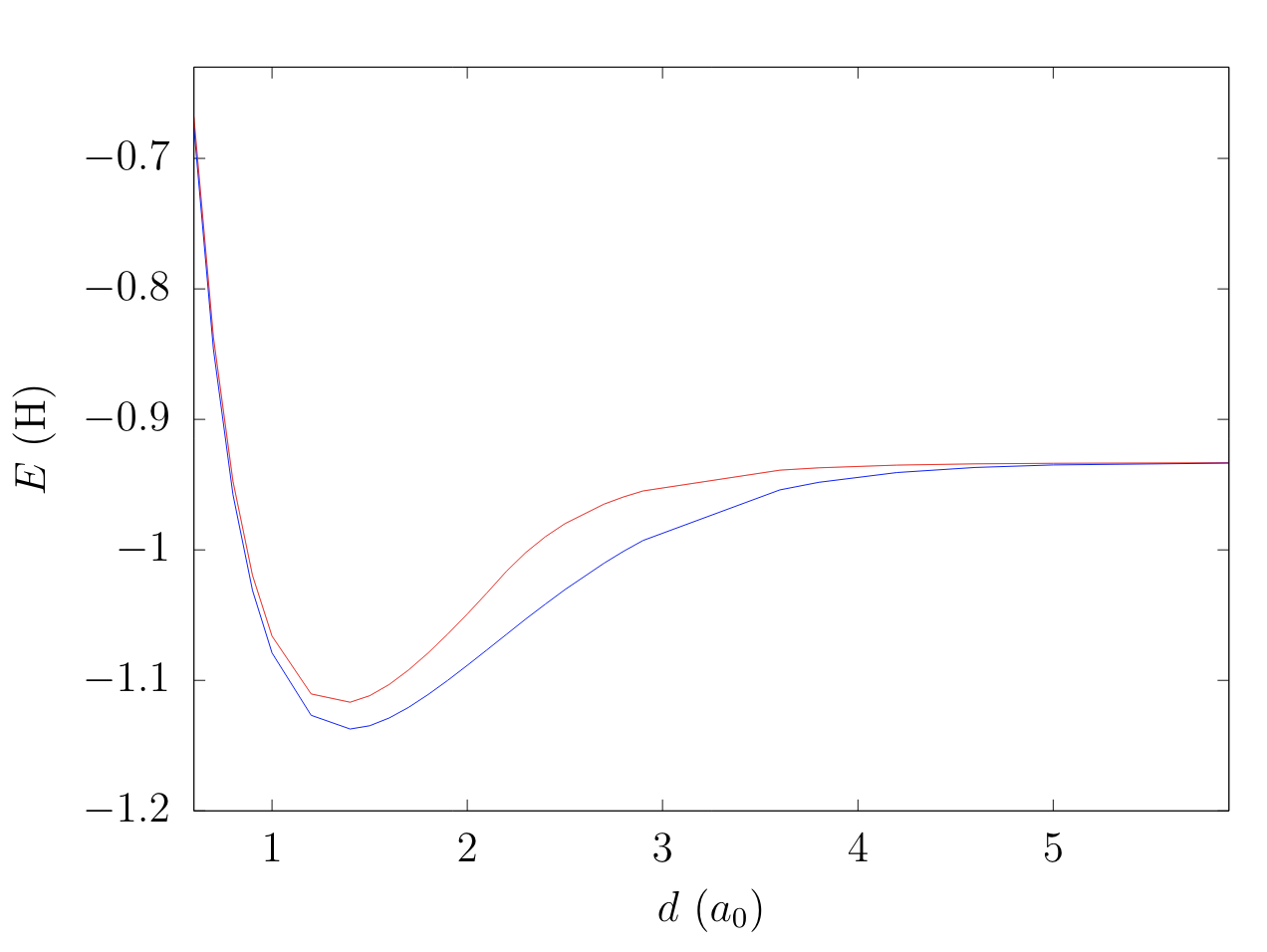
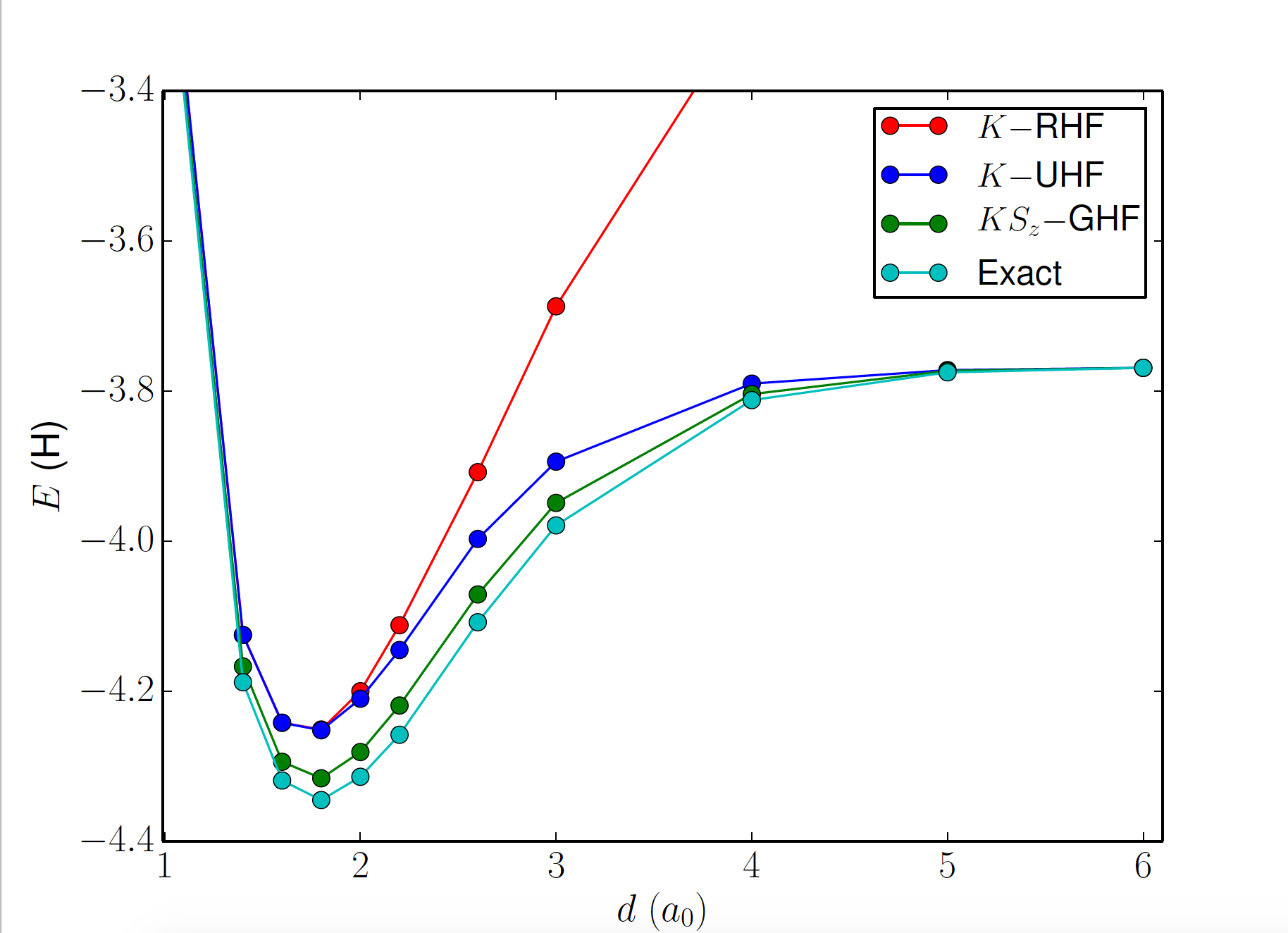
\langle\rho_{i\uparrow}\rho_{j\downarrow}\rangle = \langle\rho_{i\uparrow}\rangle\langle\rho_{j\downarrow}\rangle,
\langle\rho_{i\uparrow}\rangle=\langle\rho_{i\downarrow}\rangle
  • Doesn't break bonds correctly: \(\text{H}_2\) dissociation

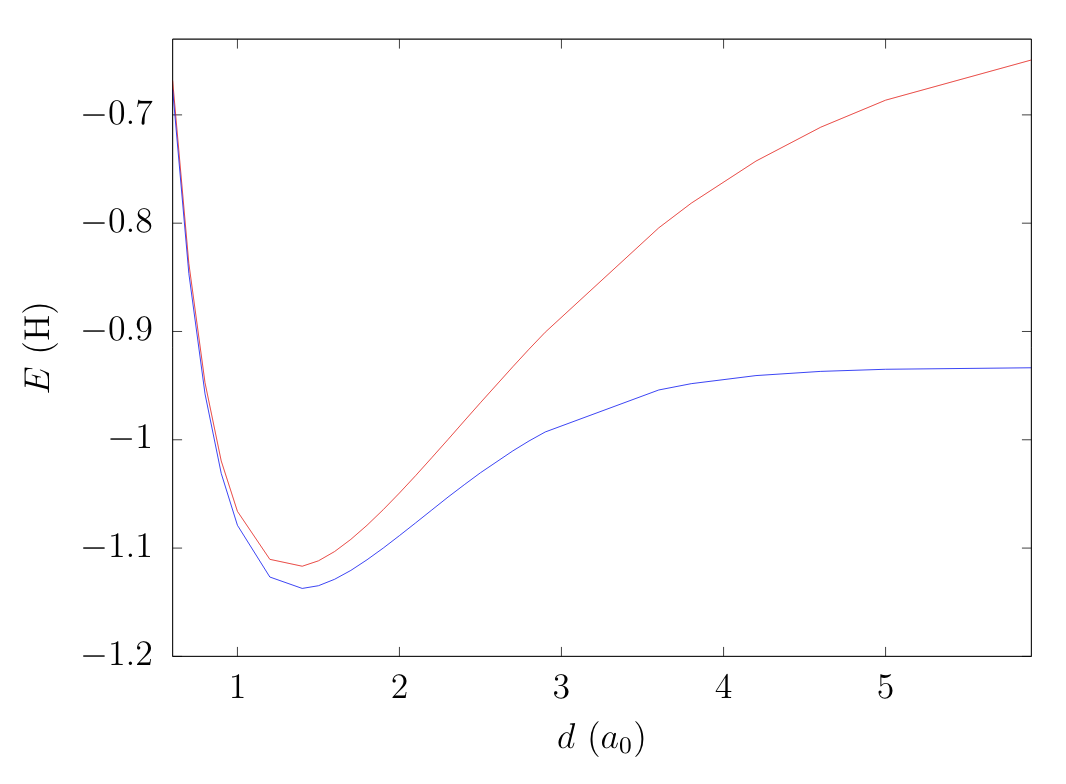
Restricted

Exact

c_{1\uparrow}^{\dagger}c_{1\downarrow}^{\dagger}|0\rangle = (a_{1\uparrow}^{\dagger}a_{2\downarrow}^{\dagger}+a_{1\downarrow}^{\dagger}a_{1\uparrow}^{\dagger}+a_{1\uparrow}^{\dagger}a_{1\downarrow}^{\dagger}+a_{2\uparrow}^{\dagger}a_{2\downarrow}^{\dagger})|0\rangle
c_{1}^{\dagger}\qquad =\quad a_{1}^{\dagger}+a_{2}^{\dagger}

as \(d\rightarrow\infty\)

Unrestricted Hartree Fock (UHF)

Singly occupied orbitals:

|\psi\rangle = c_{1\uparrow}^{\dagger}c_{1\downarrow}^{\dagger}c_{2\uparrow}^{\dagger}c_{2\downarrow}^{\dagger}\dots c_{\frac{N}{2}\uparrow}^{\dagger}c_{\frac{N}{2}\downarrow}^{\dagger}|0\rangle
c_{i\sigma}^{\dagger}=\sum_{l}\theta^{l}_{i\sigma}a^{\dagger}_{l\sigma}
\langle\mathbf{n}|\psi\rangle = \text{det}(\qquad)\text{det}(\qquad)
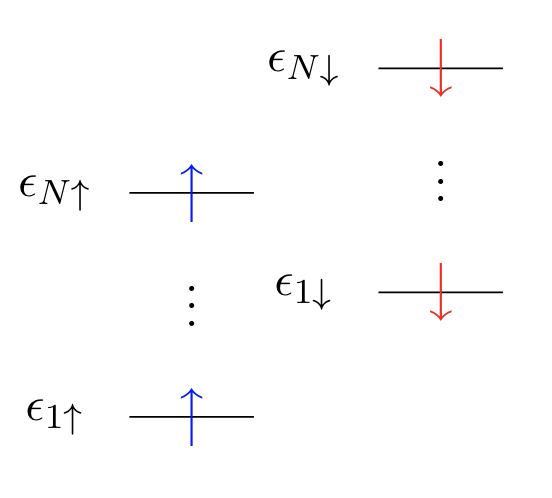
  • Correlates \(\uparrow\) and \(\downarrow\) electrons
  • Breaks bonds correctly (in many cases)

Unrestricted

Exact

c_{1\uparrow}^{\dagger}=a_{1\uparrow}^{\dagger},\ c_{1\downarrow}^{\dagger}=a_{2\downarrow}^{\dagger}

as \(d\rightarrow\infty\)

Broken symmetry 

  • Hamiltonian has spin symmetry: invariant under spin rotations
[H, \mathbf{S}] = 0

The exact ground state is a spin eigenstate.

  • The restricted wavefunction is a spin eigenstate, the unrestricted wavefunction is not. It breaks \( S^2 \) symmetry.
  • The unrestricted wavefunction is an \( S_z \) eigenstate. We can break this symmetry as well.
  • For an approximate variational wavefunction, symmetry is a constraint that can only raise its energy. In general, we can break all symmetries to remove constraints.

Generalized Hartree Fock (GHF)

|\psi\rangle = c_{1}^{\dagger}c_{2}^{\dagger}\dots c_{N}^{\dagger}|0\rangle
c_{i}^{\dagger}=\sum_{l,\sigma}\theta^{l\sigma}_{i}a^{\dagger}_{l\sigma}=\sum_{l}\left(\theta^{l\uparrow}_{i}a^{\dagger}_{l\uparrow}+\theta^{l\downarrow}_{i}a^{\dagger}_{l\downarrow}\right)
\langle\mathbf{n}|\psi\rangle = \text{det}(\qquad)

Orbitals are not \( S_z \) eigenstates, spin and space entangled

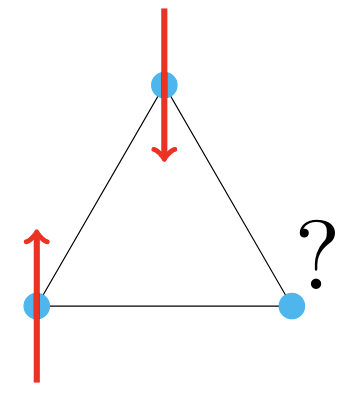
Frustrated systems:

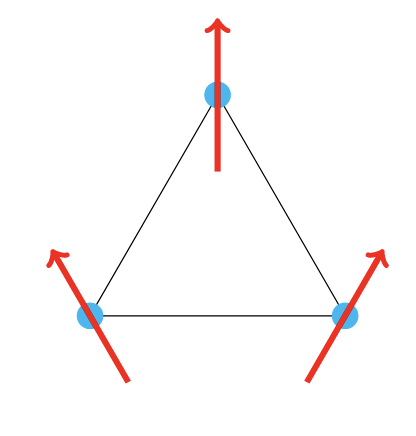
Restore broken symmetries

  • We can restore the broken symmetry by projecting onto the desired symmetry sector, thus improving the wavefunction
  • In Monte Carlo sampling, we can project certain symmetries trivially by choosing the walkers appropriately. For example, if the walkers are \(S_z\) eigenstates:
\langle\mathbf{n}|P_{S_z}|\psi\rangle = \langle\mathbf{n}|\psi\rangle
  • Breaking symmetries may lower energy, but resulting wavefunction doesn't have good quantum numbers.
  • We can break and restore complex conjugation symmetry by using complex orbitals and taking the real part of the overlap.
\langle\mathbf{n}|P_{K}|\psi\rangle = \text{Re}(\langle\mathbf{n}|\psi\rangle)

H\( _8 \) linear chain (8e, 8o)

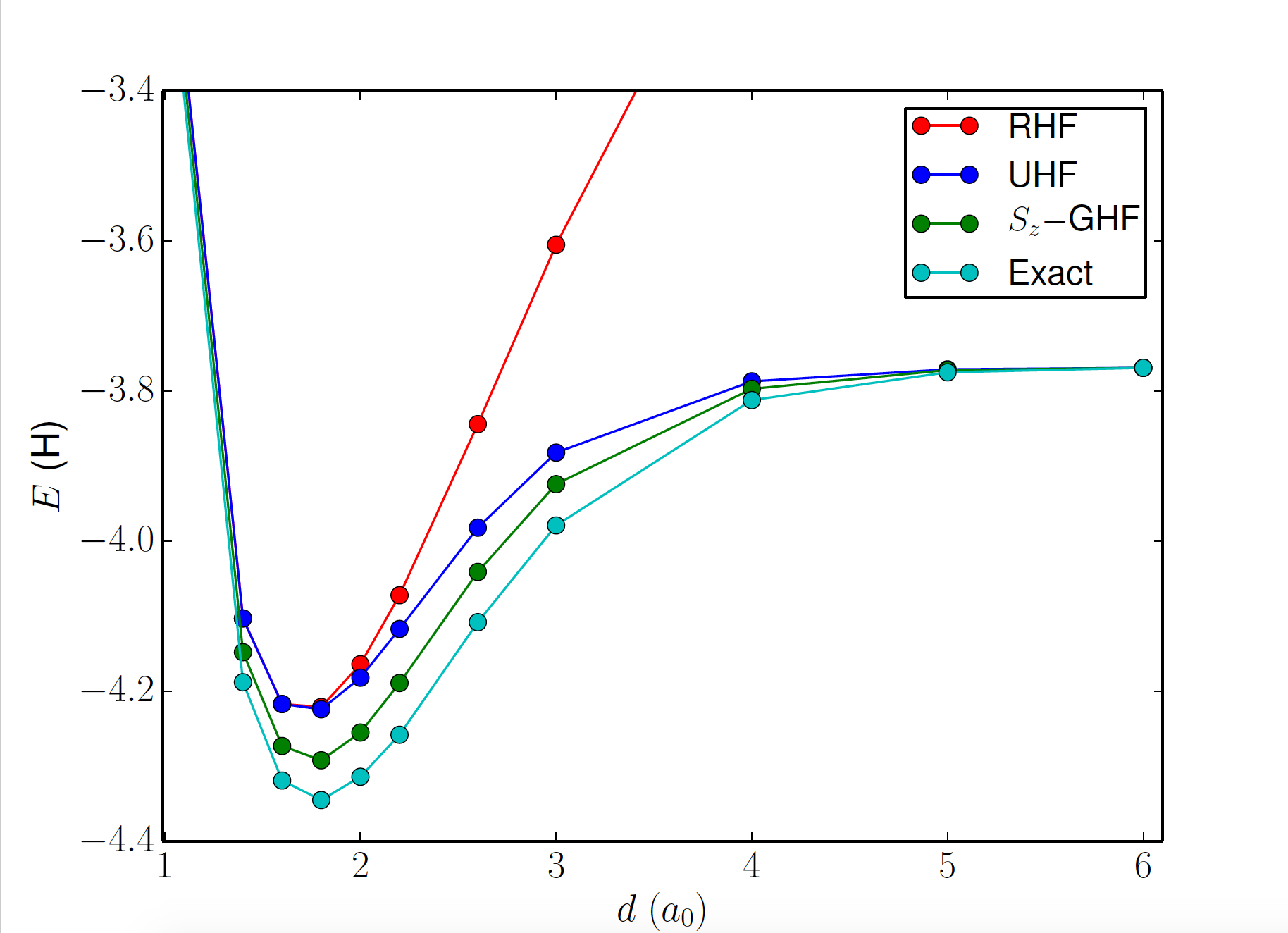
restoring \( S_z \) symmetry

restoring \( S_z \) and \( K \) symmetries

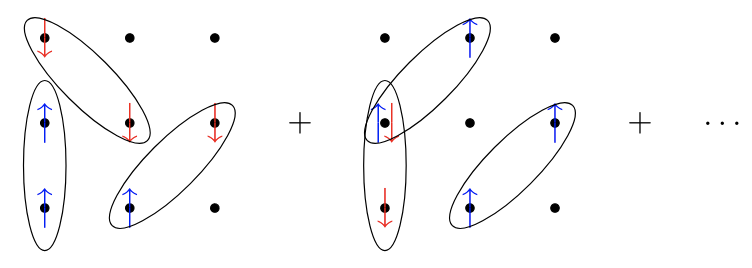
Antisymmetrized geminal power (AGP)

We can break the number symmetry as well!

|\psi\rangle = P_N\exp\left(\sum_{p,q}F_{p\uparrow,q\downarrow}a_{p\uparrow}^{\dagger}a_{q\downarrow}^{\dagger}\right)|0\rangle=\left(\sum_{p,q}F_{p\uparrow,q\downarrow}a_{p\uparrow}^{\dagger}a_{q\downarrow}^{\dagger}\right)^{N/2}|0\rangle

\( F_{p\uparrow,q\downarrow} \rightarrow\) amplitude for the bond between \( p \) and \( q \)

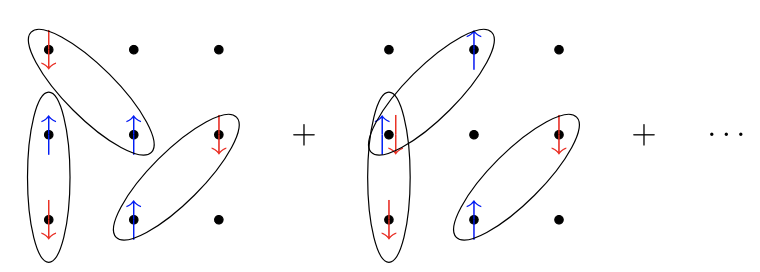
\langle\mathbf{n}|\psi\rangle = \text{det}(\qquad)

BCS wavefunction in real space

Spin eigenstate if \( F_{p\uparrow,q\downarrow} \) symmetric, breaks \( S^2 \) symmetry otherwise  

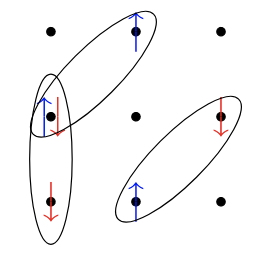
Pfaffians

Includes same spin pairing: breaks all symmetries

|\psi\rangle =\left(\sum_{p\sigma,q\gamma}F_{p\sigma,q\gamma}a_{p\sigma}^{\dagger}a_{q\gamma}^{\dagger}\right)^{N/2}|0\rangle
\langle\mathbf{n}|\psi\rangle = \text{pfaffian}(\qquad) = \pm\left[\text{det}(\qquad)\right]^{1/2}

antisymmetric matrix

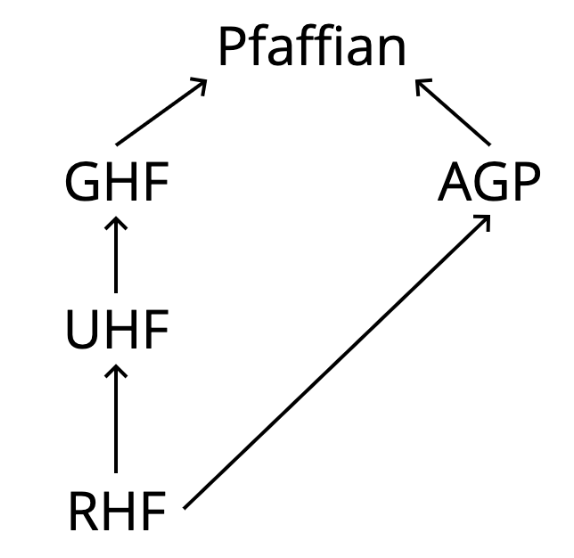
The most general mean field wavefunction: includes all others as special cases

Jastrow factor

\hat{\mathcal{J}}|\psi\rangle = \exp\left(\sum_{p\sigma,q\gamma} v_{p\sigma,q\gamma}\hat{n}_{p\sigma}\hat{n}_{q\gamma}\right)|\psi\rangle

counts site occupations and suppresses spurious ionic configurations (double occupations)

also correlates long range excitations: important for describing insulators

Wavefunction hierarchy

|\psi\rangle=\hat{\mathcal{J}}\hat{P}|\phi\rangle

jastrow

projector

reference

General form:

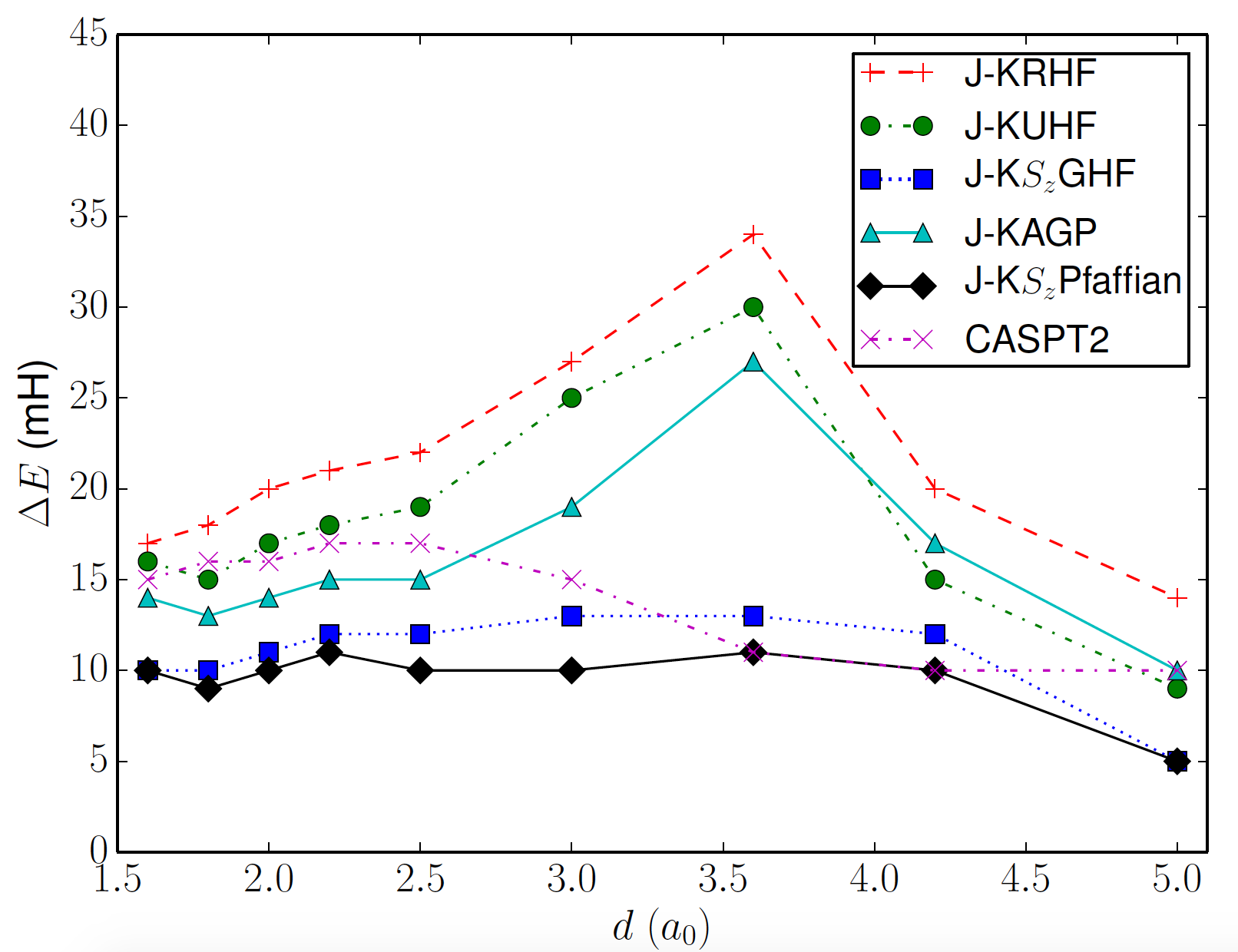
N\( _2 \) (14e, 18o)

d (Bohr) Exact Jastrow-KSPfafian Green's function MC
1.6 -0.5344 -0.5337 -0.5342
1.8 -0.5408 -0.5400 -0.5406
2.5 -0.5187 -0.5180 -0.5185

H\( _{50} \) linear chain (50e, 50o)

U Accurate result Jastrow-
KSGHF		 Green's function MC
2 -1.1962 -1.1920 -1.1939
4 -0.8620 -0.8566 -0.8598
8 -0.5237 -0.5183 -0.5221

2D Hubbard: 98 sites

Thank you!