Structure and dynamics of electron-phonon coupled systems using neural quantum states

Ankit Mahajan

Reichman Group, Columbia University

 AM, Robinson, Lee, Reichman arXiv:2405.08701

Introduction

V_{e-\text{lattice}}= \sum_n V(r_e-R_n-\delta R_n)\approx \sum_n V(r_e-R_n)-\delta R_n.\nabla V(r_e-R_n)
H_{\text{lattice}} \approx -\sum_n \frac{\nabla_n^2}{2} + \sum_{n,m}\frac{1}{2}\delta R_n. D_{mn}.\delta R_m

Quantum many-body effects:

Riley, et al. Nature Communications  9(1), 2305 (2018)

Li, et al. PRL 122, 186402 (2019)

Electron-lattice interaction using linear approximation

Lattice energy within harmonic approximation

Outline

  • Models, wave functions, and methods
  • Ground state properties
  • Excited states and dynamical properties

Model Hamiltonians

Using a Bloch basis

H_{\text{eph}} = g_{kq}c_{k+q}^{\dagger}c_{k}\left(b^{\dagger}_{-q} + b_{q} \right)
H_e = \epsilon_{k}c_{k}^{\dagger}c_{k}\qquad H_{\text{ph}} = \omega_{q}b_{q}^{\dagger}b_{q}

Local lattice Hamiltonians (in the site basis)

  • Holstein: density coupling
g c^{\dagger}_ic_i(b_i^{\dagger}+b_i)
  • SSH : phonon modulated hopping
g (c_i^{\dagger}c_j + \text{h.c.})(x_i-x_j)
  • Bond model: phonons on bonds
g(c_i^{\dagger}c_j + \text{h.c.})x_{\langle ij\rangle}
  • Dilute limit: polaron and bipolaron effects 
H_{\text{Hubbard}} = Un_{i\uparrow}n_{i\downarrow}
  • Dense limit: interplay of e-e and eph interactions

Fillings

Neural quantum states and VMC

|\psi_{\text{NQS}}\rangle = \sum_{w} \frac{\exp{(f(w, \mathbf{p}))}}{\sqrt{\prod_iw_{\nu}^i!}} |w\rangle
f(w, \mathbf{p}) = NN_r(w, \mathbf{p}) + iNN_{\phi}(w, \mathbf{p})
  • Symmetry projection: drastically improves performance
\psi^S(w)=\frac{1}{N}\sum_g c_g \psi(g.w)
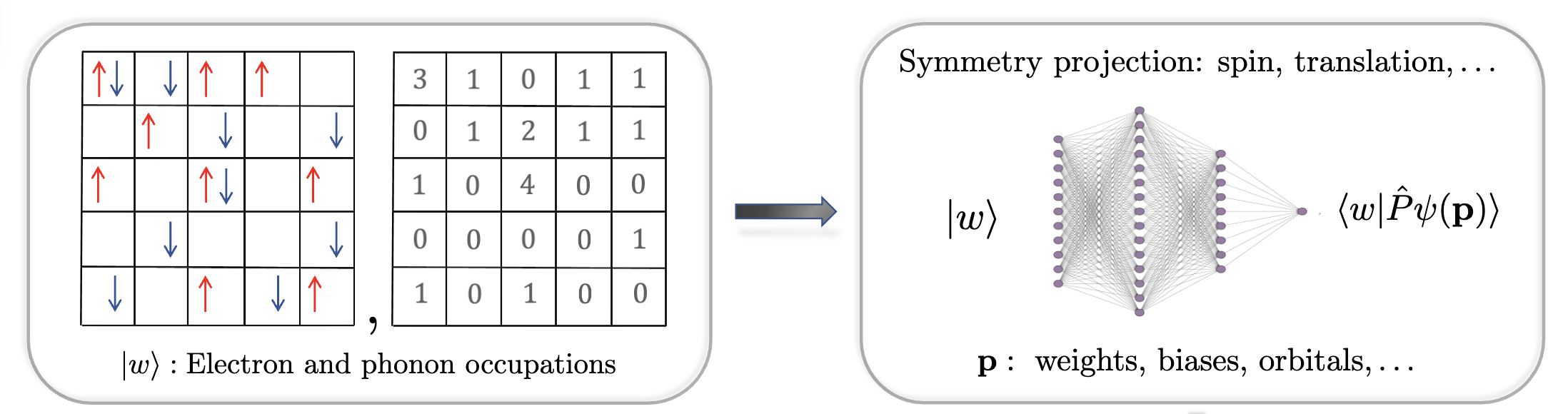
  • TP-NQS with one hidden neuron is equivalent to the Toyozawa state
|\psi_{\text{Toyozawa}}^k\rangle=P_k\left(\sum_i \phi_i c_i^{\dagger}\right) \exp \left(-\sum_{\nu}\xi_{\nu}b_{\nu}^{\dagger} - \xi_{\nu}^*b_{\nu}\right)\ket{0}
\frac{\langle \psi|O|\psi\rangle}{\langle \psi|\psi\rangle} = \sum_{w} \frac{|\langle\psi|w\rangle|^2}{\langle\psi|\psi\rangle}\frac{\langle w|O|\psi\rangle}{\langle w|\psi\rangle}
\frac{\langle w|O|\psi\rangle}{\langle w|\psi\rangle} = \sum_{w'}\langle w|O|w'\rangle\frac{\langle w'|\psi\rangle}{\langle w|\psi\rangle}

For polarons and bipolarons, cost of energy calculation with translational symmetry ~ cost in the momentum basis 

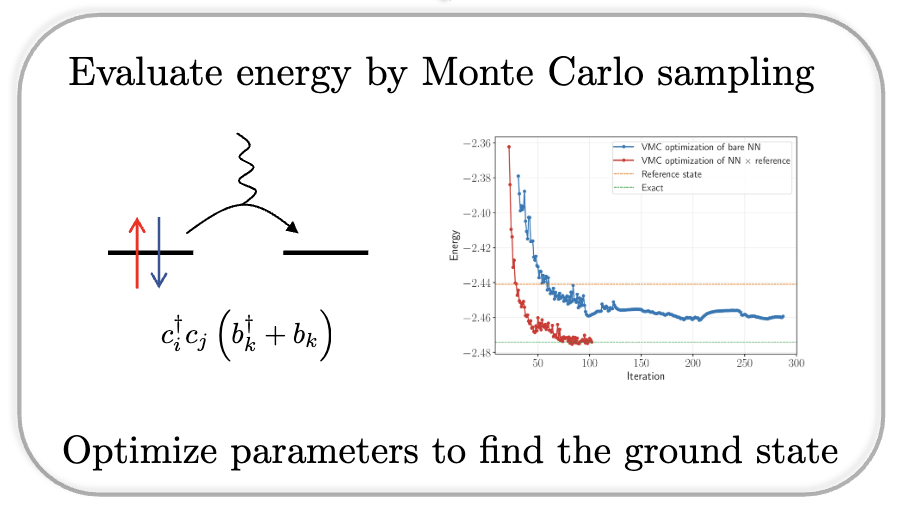
Rejection free sampling, AMSGrad optimization

  • For dense systems, we use a GHF reference:
\langle w|\psi\rangle = \langle w|\psi_{\text{NQS}}\rangle \langle w_e|\psi_{\text{GHF}}\rangle
  • e-e and e-ph Jastrows can also be efficiently represented using NQS

Variational Monte Carlo:

Outline

  • Models, wave functions, and methods
  • Ground state properties
  • Excited states and dynamical properties

30 site chain, \(\omega_0=0.5\)

Holstein

Bond

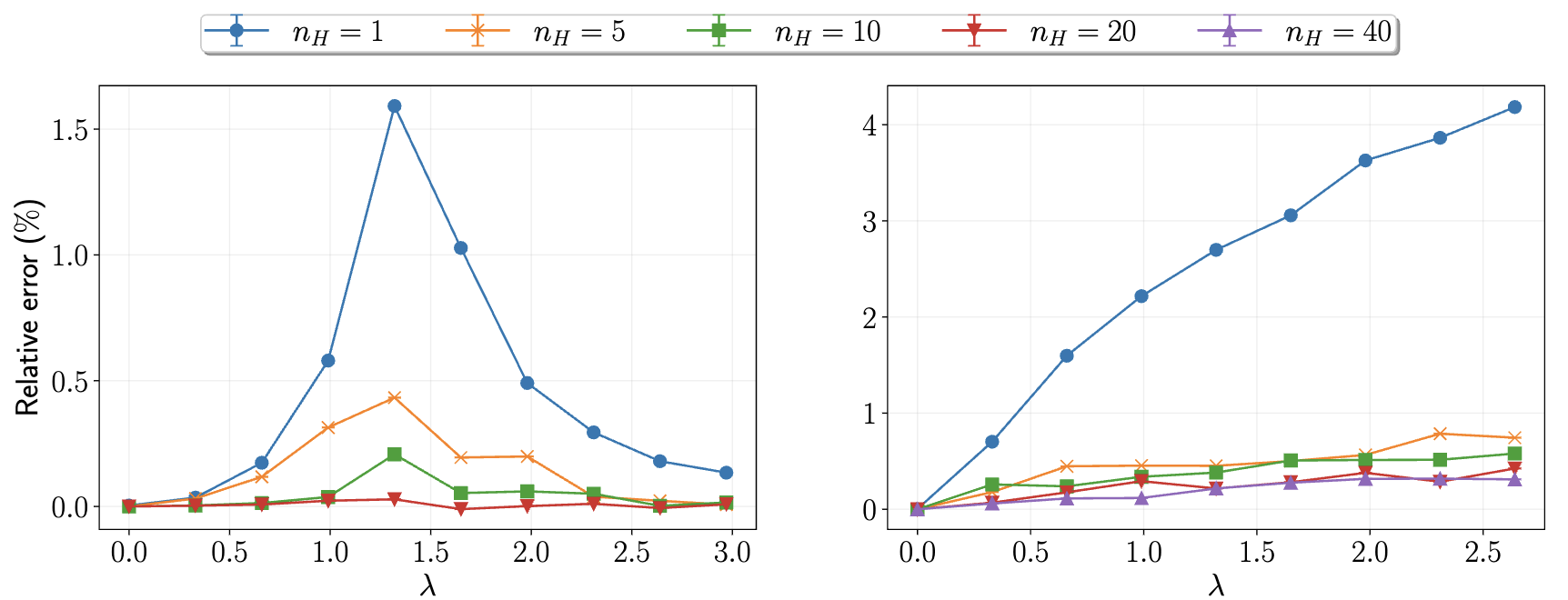
Convergence with the number of hidden neurons:

DQMC: Zhang, et al. Physical Review B (2021)

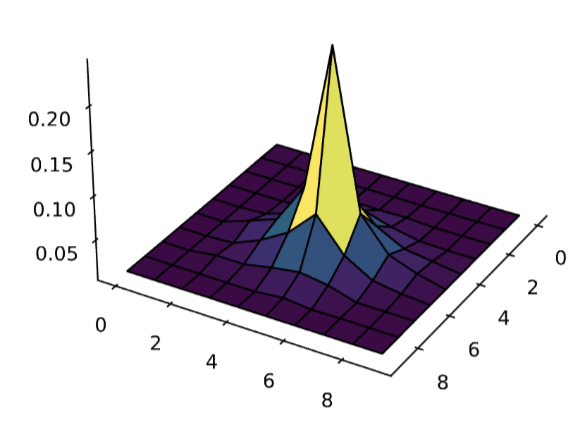
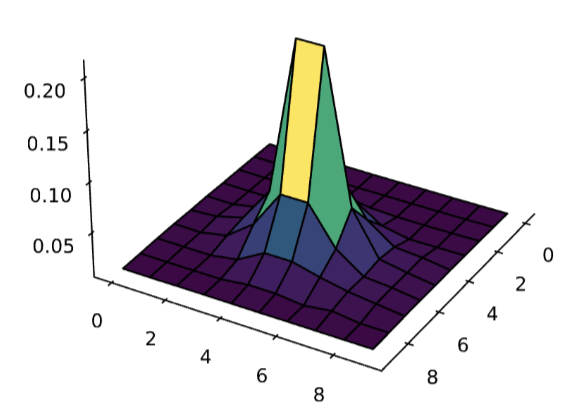
Polaron binding energy

Self-trapping: 10x10 square lattice

Lithium fluoride hole polaron

Ab initio model with 3 e and 6 \(\nu\) bands

Other estimates: 1.98 eV (DFPT), 2.2 eV (GFPT), 1.96 eV (CSPT2)

13x13x13

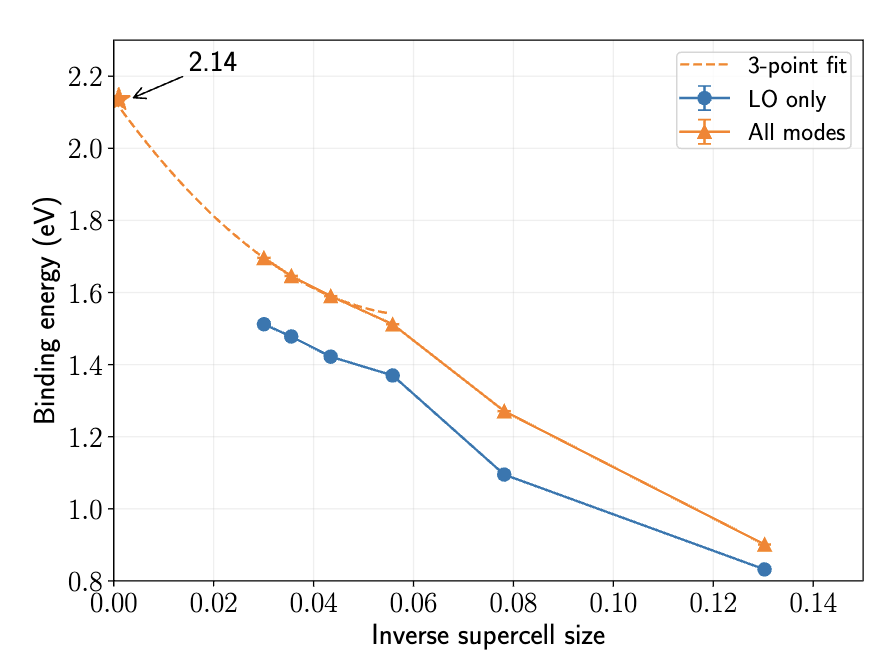
Sio, et al. PRL (2019), Lafuente-Bartolome, et al. PRL (2022), Lee, et al. Phys. Rev. Mat. (2021)

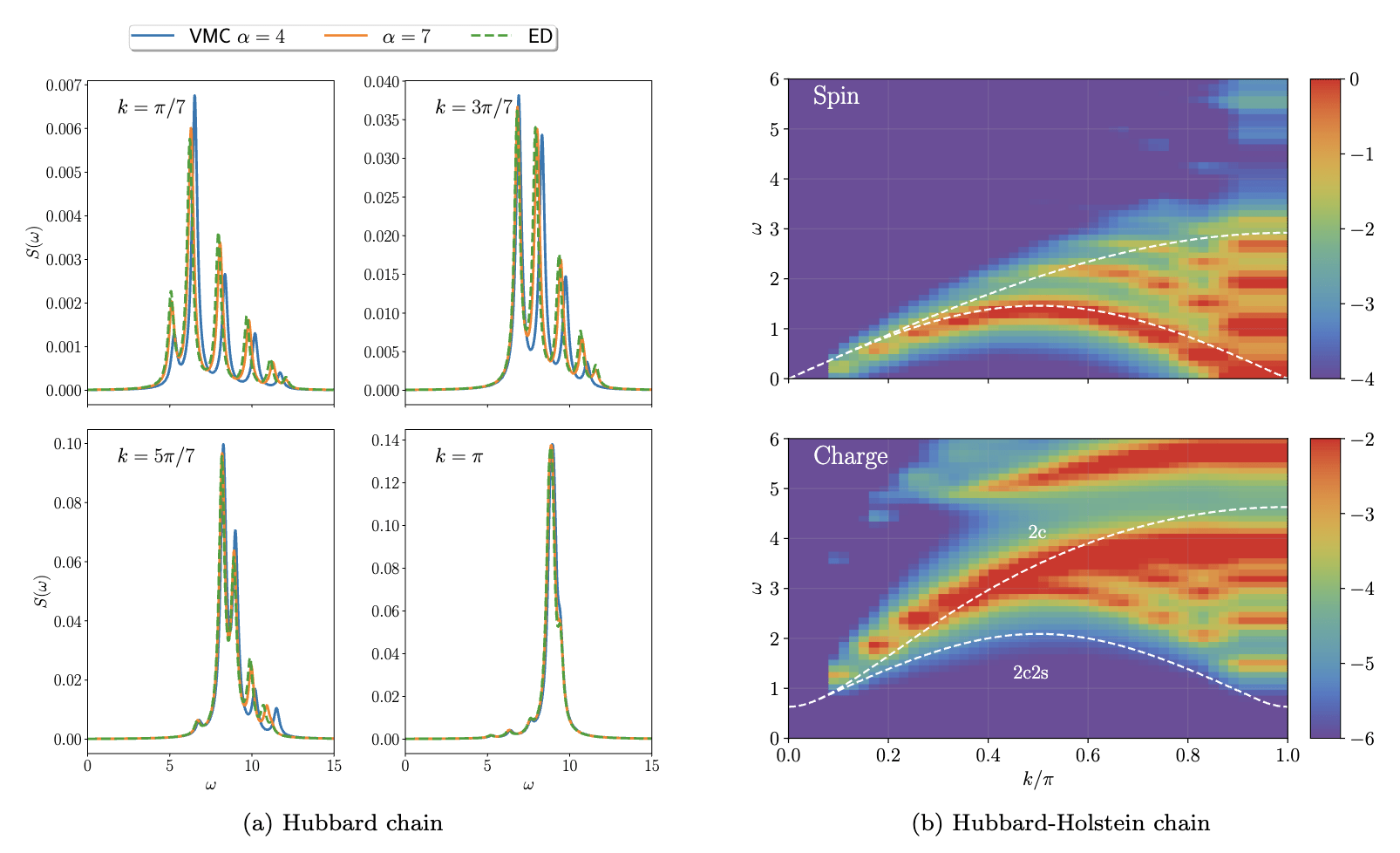
Half-filled, 20 site chain, \(\omega_0=1, U=4\) 

SDW \(\rightarrow\) CDW

AFQMC: Lee, et al. Physical Review B (2021)

Hubbard-Holstein model

Outline

  • Models, wave functions, and methods
  • Ground state properties
  • Excited states and dynamical properties

LR-VMC: excited states and dynamic properties

\ket{\psi_{\mu}} = \frac{\partial \ket{\psi_0}}{\partial p_{\nu}}
\mathbf{H}\mathbf{C} = E\mathbf{S}\mathbf{C},

Calculation of \(\langle w|H|\psi_{\nu}\rangle\) for all \(\nu\) can be performed at the same cost as energy by using reverse mode AD!

Tangent space of the NQS ansatz provides a natural subspace for describing low-lying excitations

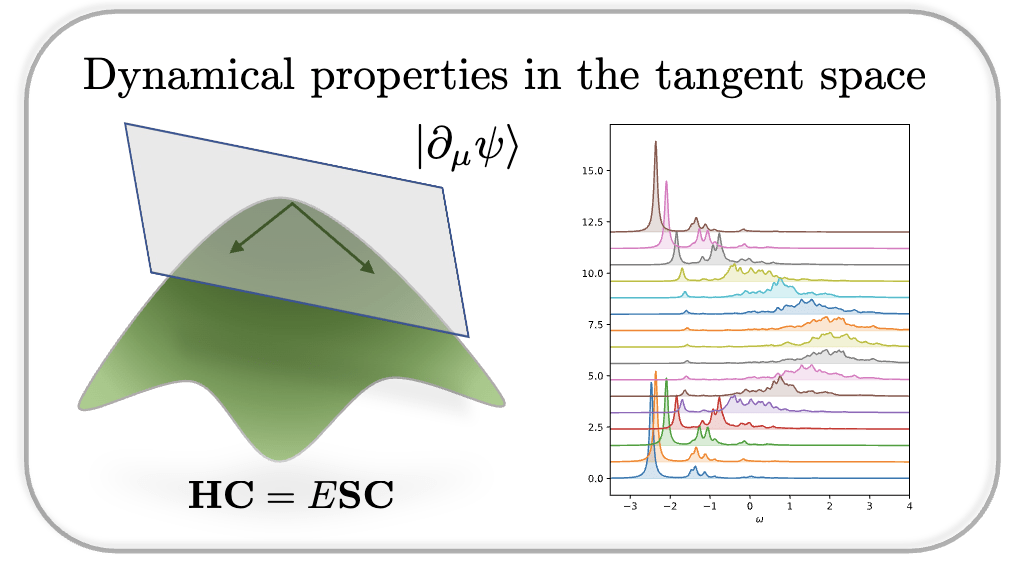
Convergence of the one particle spectral function

Bond polaron: 8 sites, \(\omega_0=1\), \(\lambda=1\), \(\eta=0.05\)

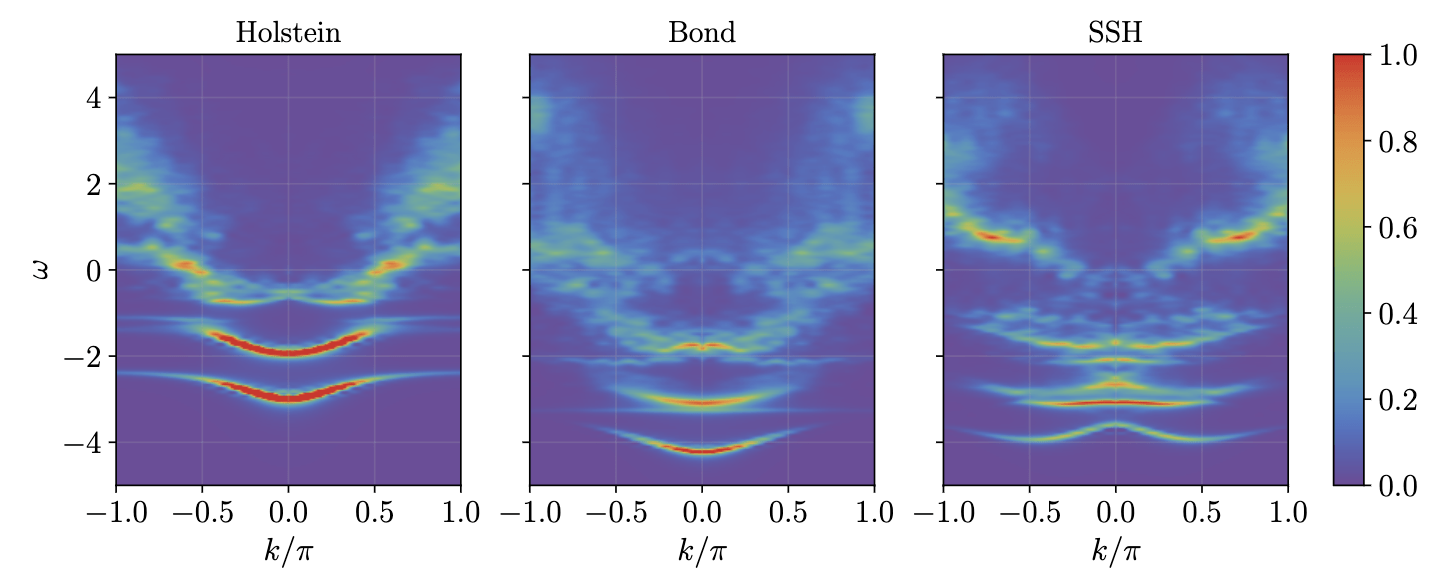
LR-VMC polaron spectral functions on a 30 site chain, \(\omega_0=1\), \(\lambda=1\) 

Hubbard-Holstein model 

Dynamical spin and charge structure factors for a half-filled 30 site chain, \(\omega_0=5, \lambda=0.25\), and \(U=4\)

Summary

  • NQS can be used to describe a range of eph interactions accurately and efficiently
  • This method can be used to perform ab initio calculations with non-trivial systems
  • It allows the calculation of dynamical properties as a natural extension of the ground state method
  • Future work will focus on finite temperature properties and better description of electron correlation within NQS

Thank you!