Properties and excited states in AFQMC
Ankit Mahajan
Reichman group, Columbia University
Stochastic electronic structure methods workshop
Two parts
Selected CI trials and excited states in AFQMC
Response formalism for properties in AFQMC
with Sandeep Sharma
with David Reichman, Shiwei Zhang, Sandeep Sharma, Joonho Lee
Ab initio AFQMC

sign problem \(\rightarrow\) phaseless constraint \(\rightarrow\) trial dependent bias

Shee et al. JCTC '19
Lee et al. JCTC '19

Hao et al. PRB '20
\(x_{\gamma}\): auxiliary field
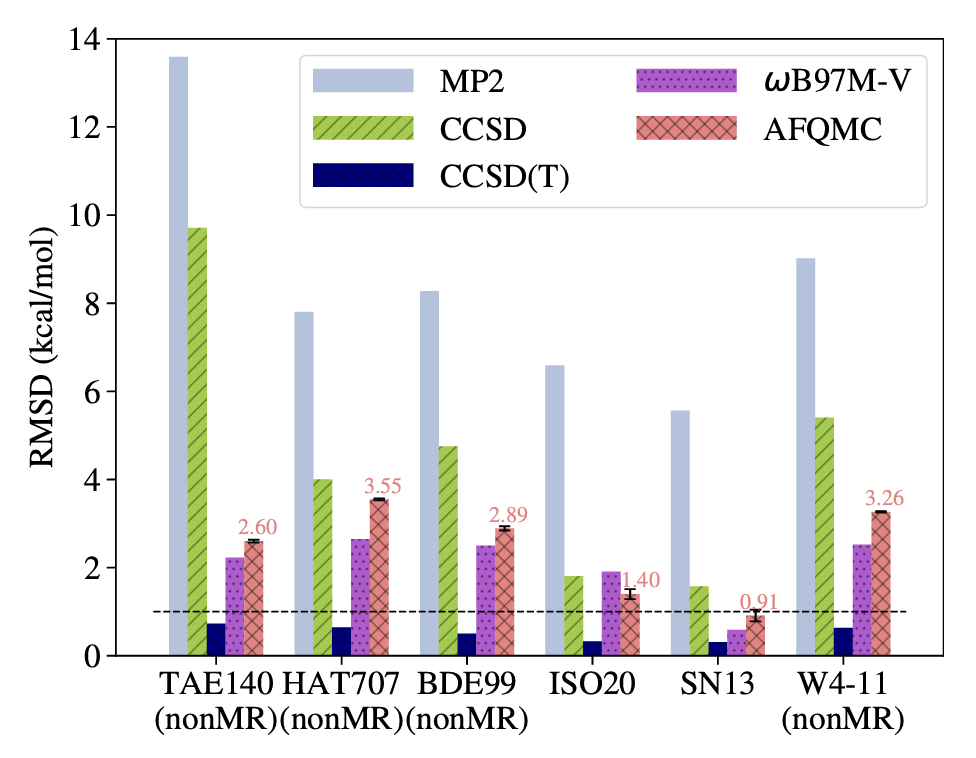
Lee, et al. Journal of Chemical Theory and Computation 18.12 (2022)
For single reference molecules, AFQMC/HF is usually more accurate than CCSD
Properties in AFQMC
- Mixed estimator:
- Backpropagation:
- Response formulation:
1. Analytical derivatives
2. Finite difference with correlated sampling: multiple calculations for different observables
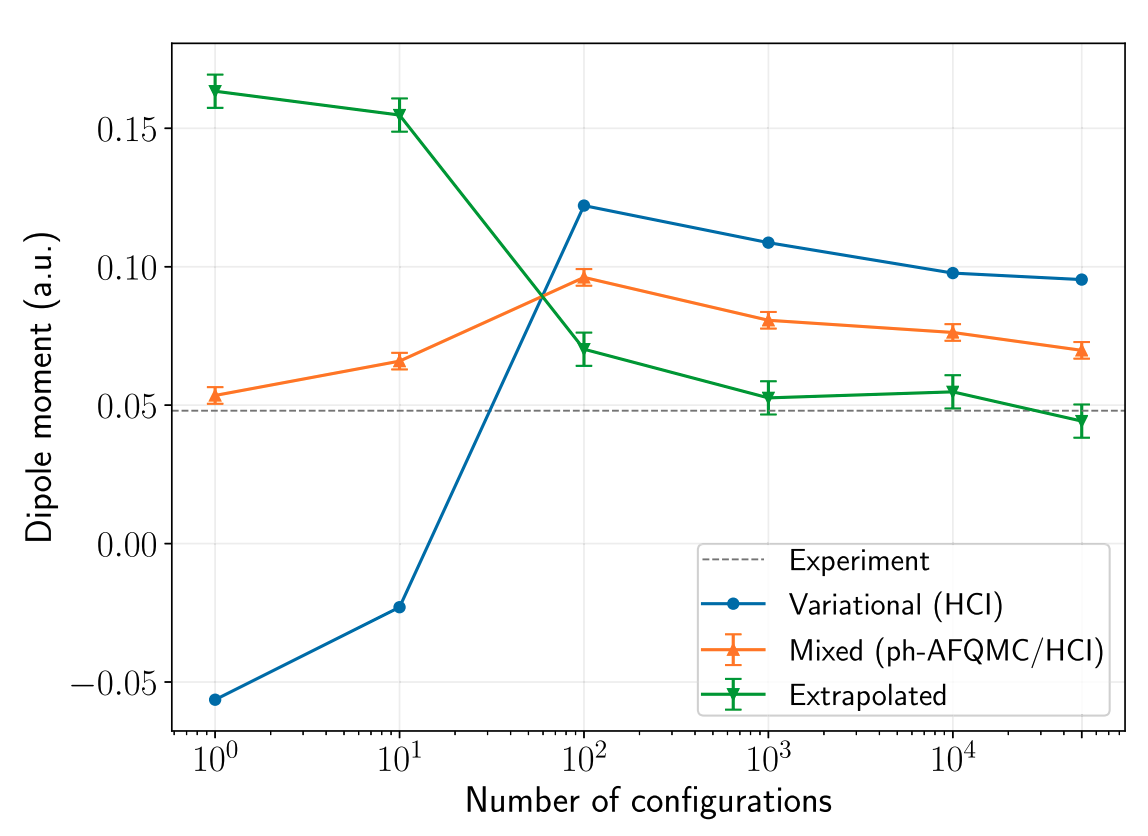
AM, Lee, Sharma JCP '22
CO (aQZ)

Adjoint algorithmic differentitation
Inputs: integrals, random numbers,...
Output: AFQMC energy
Adjoint mode: cost scaling same as that of energy \(\rightarrow\) 1-RDM at the cost of energy!
Sorella, Capriotti JCP '10; Song, Martinez, Neaton JCP '20; Zhang, Chan '22; ...
calculate gradients in the reverse sweep
| # H | Finite difference | AD AFQMC w/o SR | AD AFQMC w/ SR |
| 10 | -31.4545(8) | -31.45513(9) | -31.45675(6) |
| 20 | -81.786(1) | -81.7873(2) | -81.7891(1) |
| 30 | -139.6266(3) | -139.6285(2) |
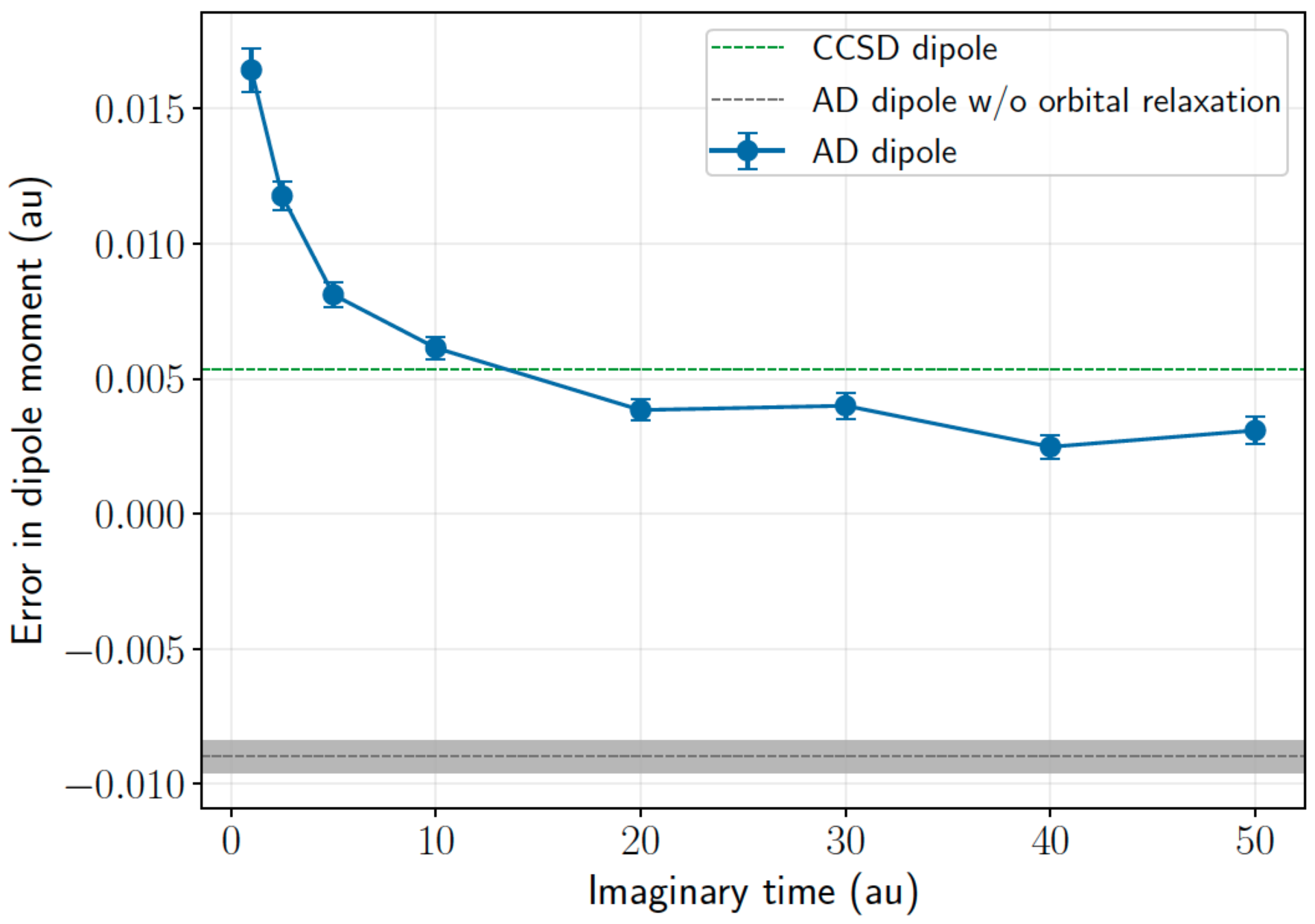
Systematic error in ammonia dipole moment (dz basis)
changes in the trial due to perturbation
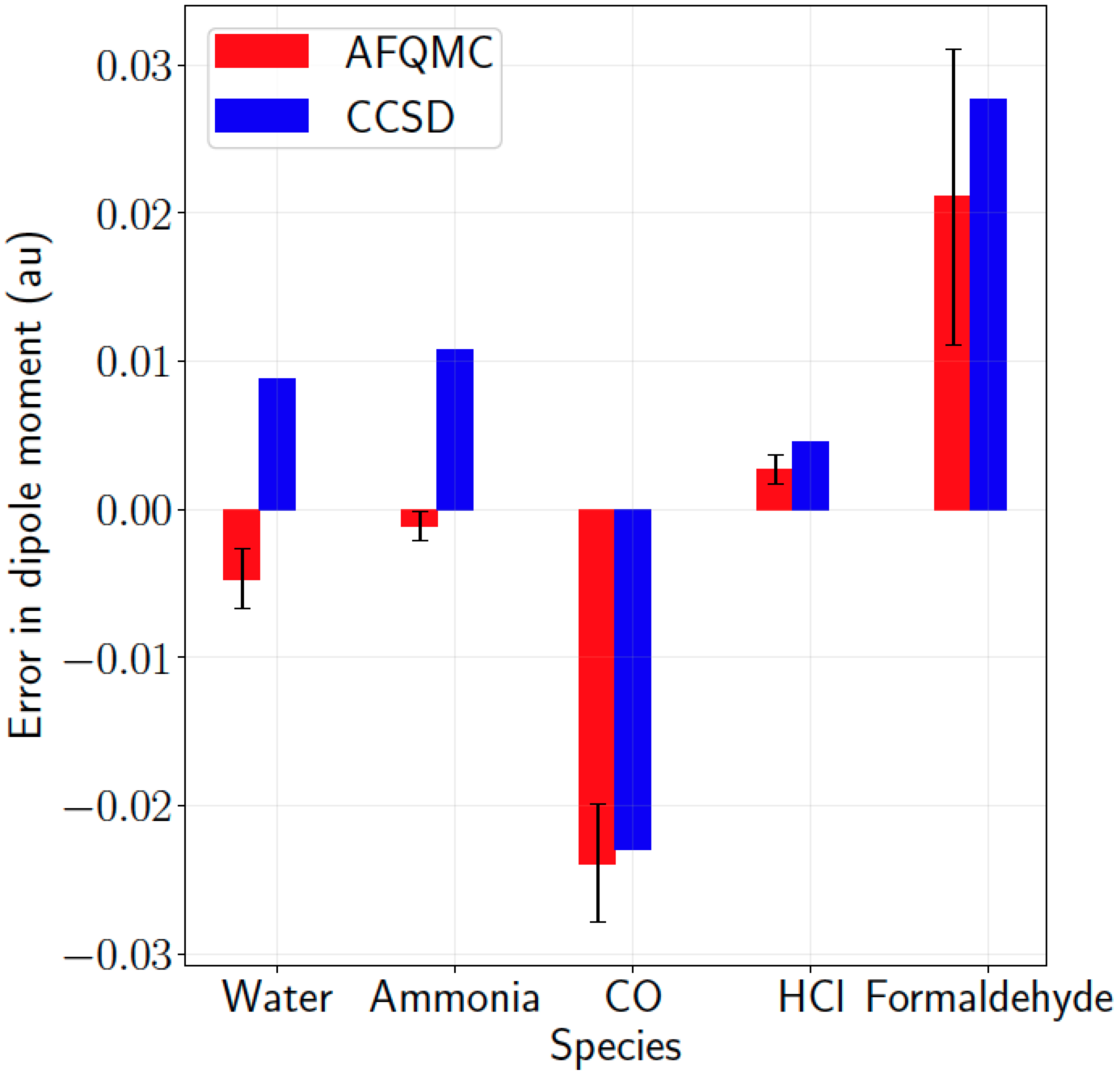
Dipole moments in the continuum limit
Self-consistent AFQMC
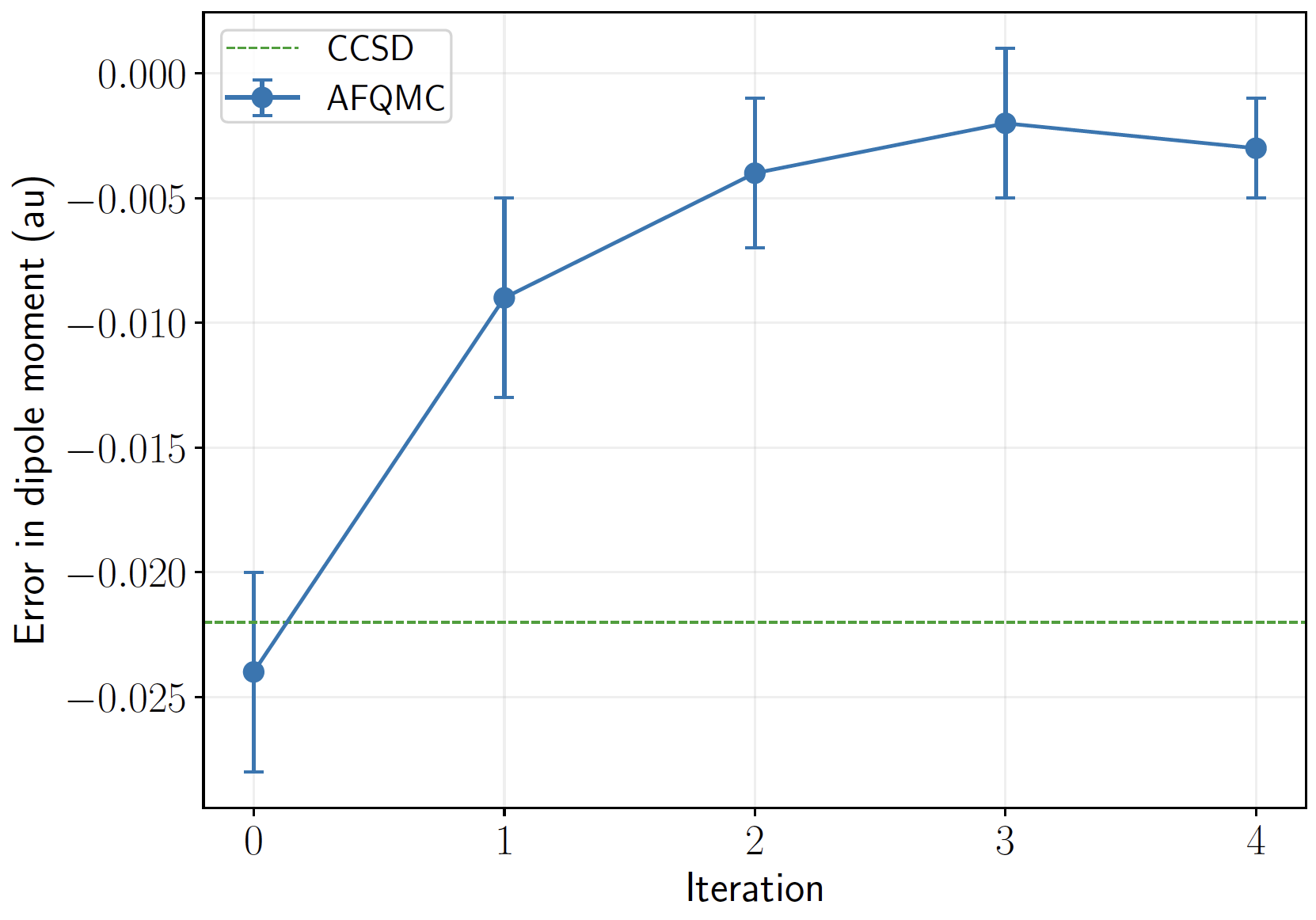
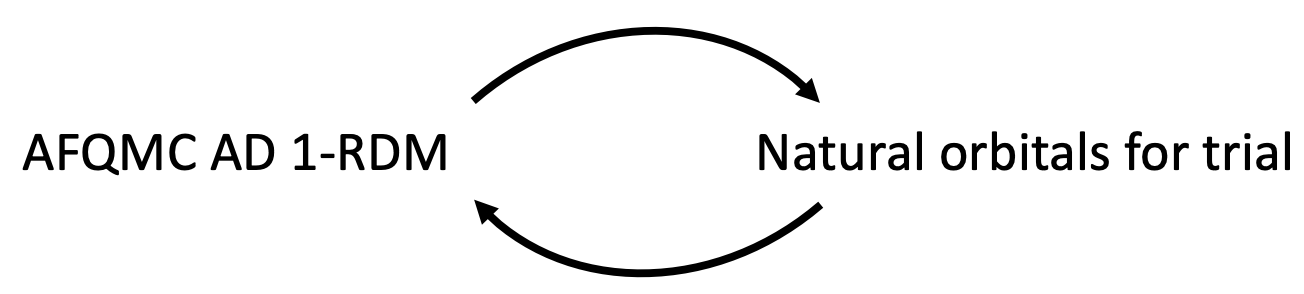
CO (aTZ)
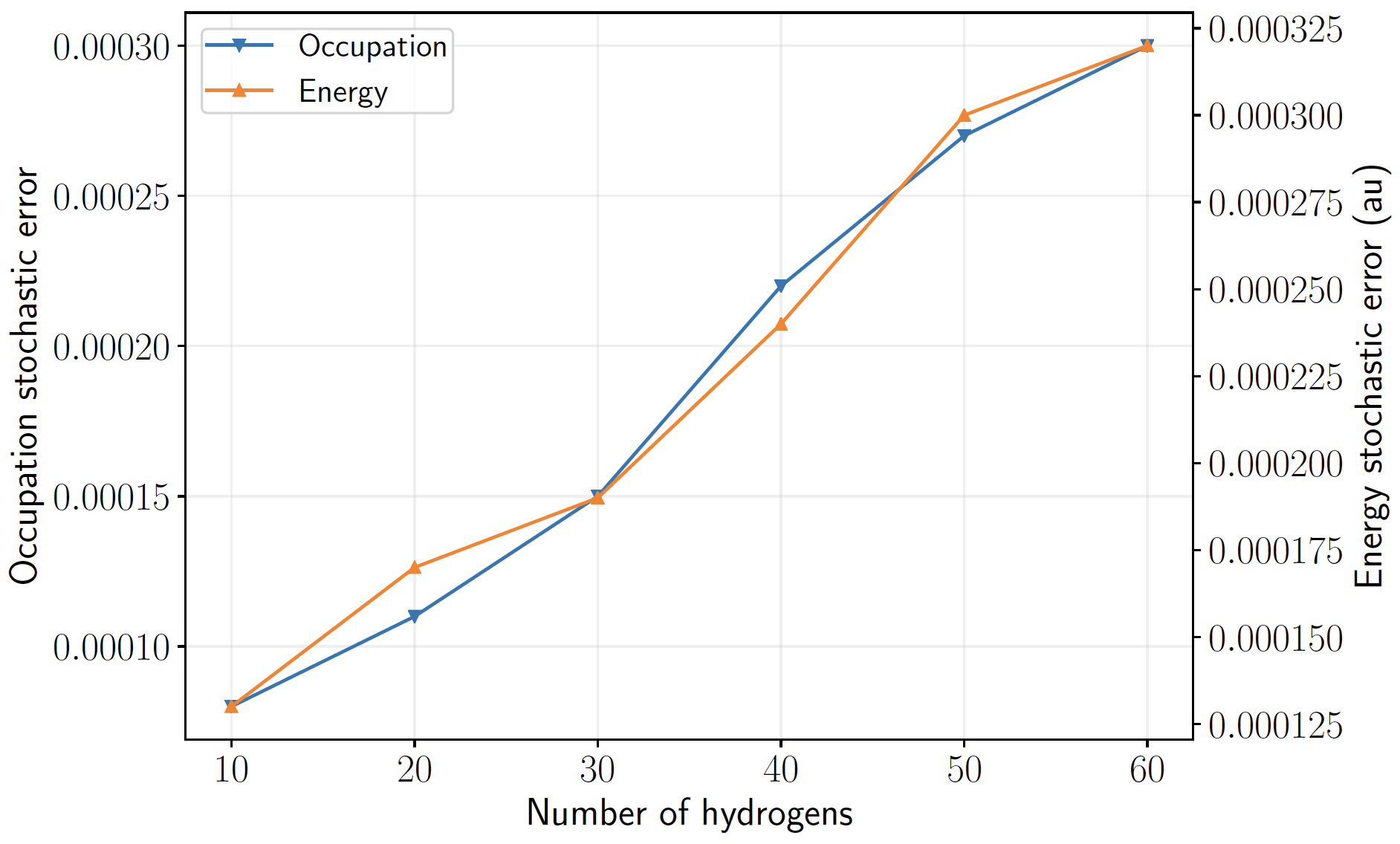
Stochastic error scaling with system size
Hydrogen chains in minimal basis, \(d =1.6\) au
comparison of scaling of stochastic error in energy vs site occupation
Systematic error scaling with system size
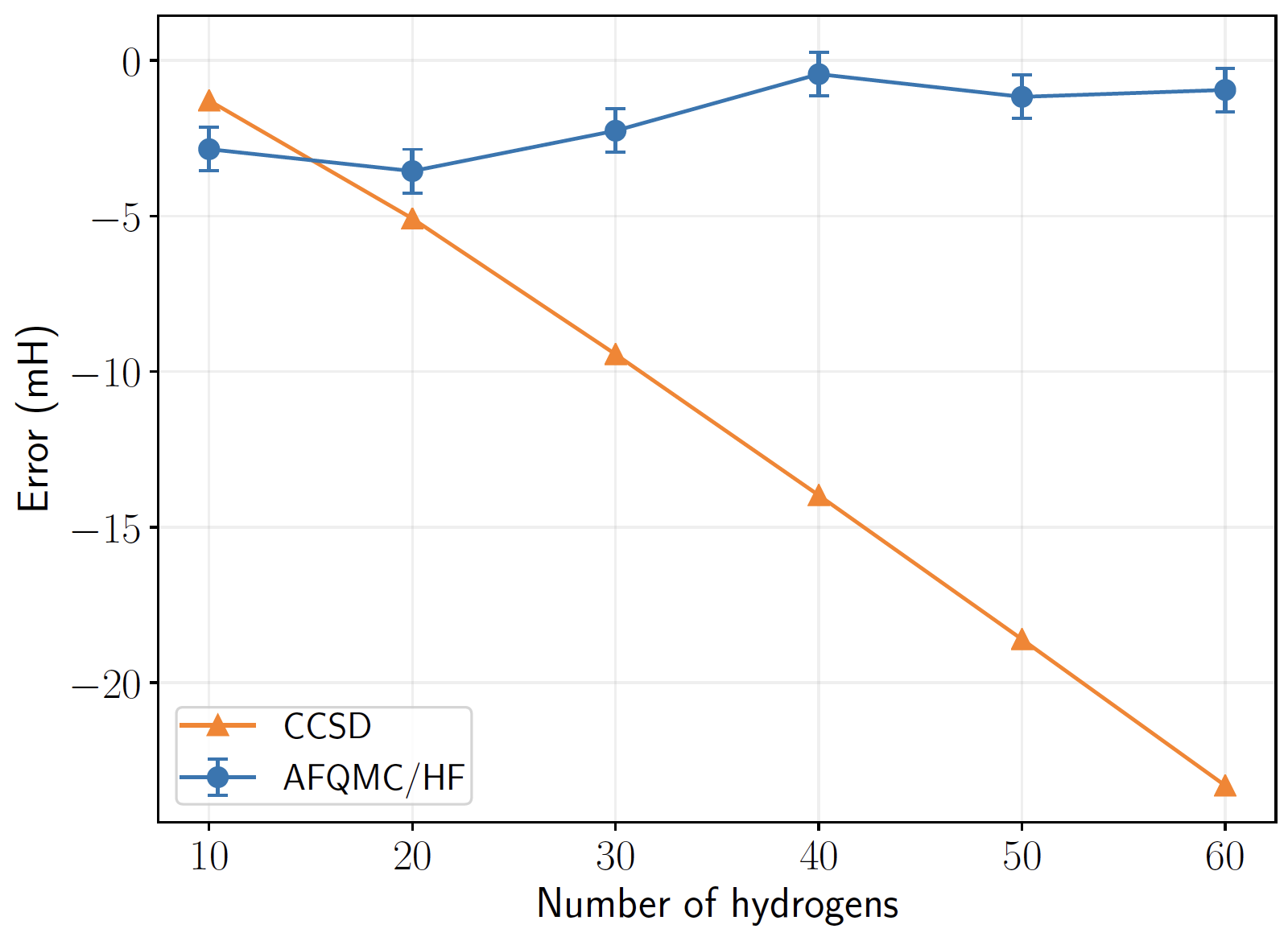
1e energy of hydrogen chains
Two parts
Selected CI trials and excited states in AFQMC
with David Reichman, Shiwei Zhang, Sandeep Sharma, Joonho Lee
Response formalism for properties in AFQMC
with Sandeep Sharma
- Include the most important configurations using particle-hole excitations
Selected CI trials
- In real space QMC: reduced cost scaling due to the algorithm of Filippi, Assaraf, Moroni (JCP '16)
- In AFQMC: cost of single determinant trial local energy is \(O(N^4)\). Can we avoid \(O(N_dN^4)\)?

\(O(NN_d+N^4)\)
- Yes, we can!
AM, Sharma JCTC '21
AM, Lee, Sharma JCP '22
\(\text{H}_{50}\) (50e, 50o)

AM, Lee, Sharma JCP '22
\(^1A_g \rightarrow ^1B_u\)
Butadiene (22e, 142o)

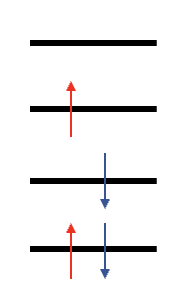
Open-shell singlet excited states
Modified AFQMC
AFQMC propagation
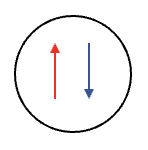
collapses to closed-shell
open-shell walker

Projection to prevent collapse:
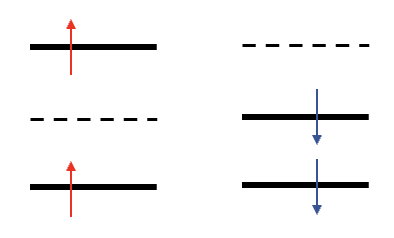
orthogonalize periodically to inserted orbitals
Ma, Zhang, Krakauer '13
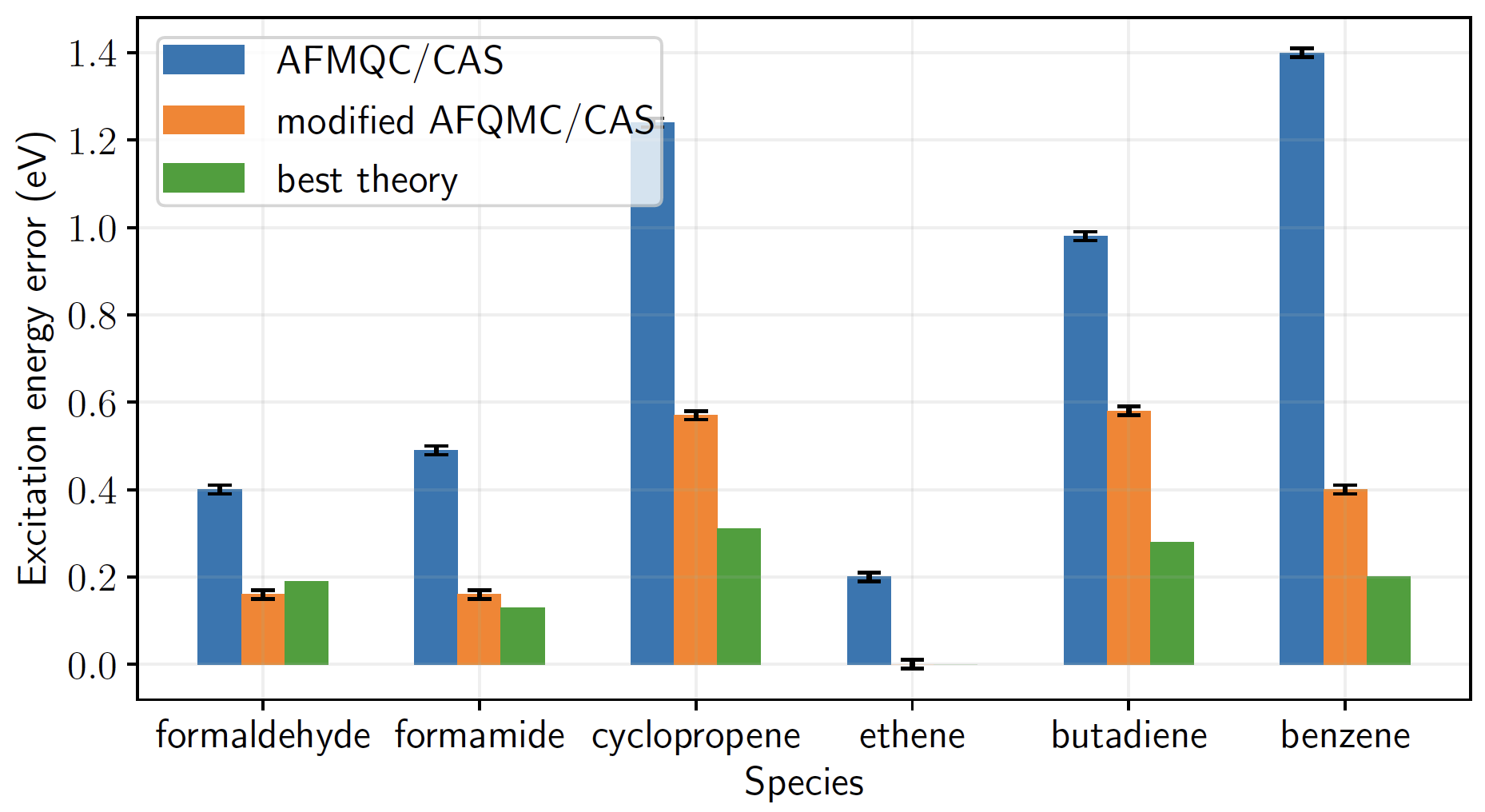
Minimal CAS trials
Open-shell singlet excited states