Systematically Improvable Auxiliary Field Quantum Monte Carlo
Ankit Mahajan
Reichman Group
Columbia University
Battery center meeting
Two parts
Selected CI trial states in AFQMC:
what are they good for and how to use them
with Sandeep Sharma, Joonho Lee, Jo Kurian
Response formalism for properties in AFQMC:
ground state properties using algorithmic differentiation
with Sandeep Sharma
Ab initio AFQMC
sign problem → phaseless constraint → trial dependent bias
single determinant trial most commonly used
Shee et al. JCTC '19
Lee, Malone, Morales JCTC '19
Malone, Benali et al. PRB 2020
Diamond correlation energy
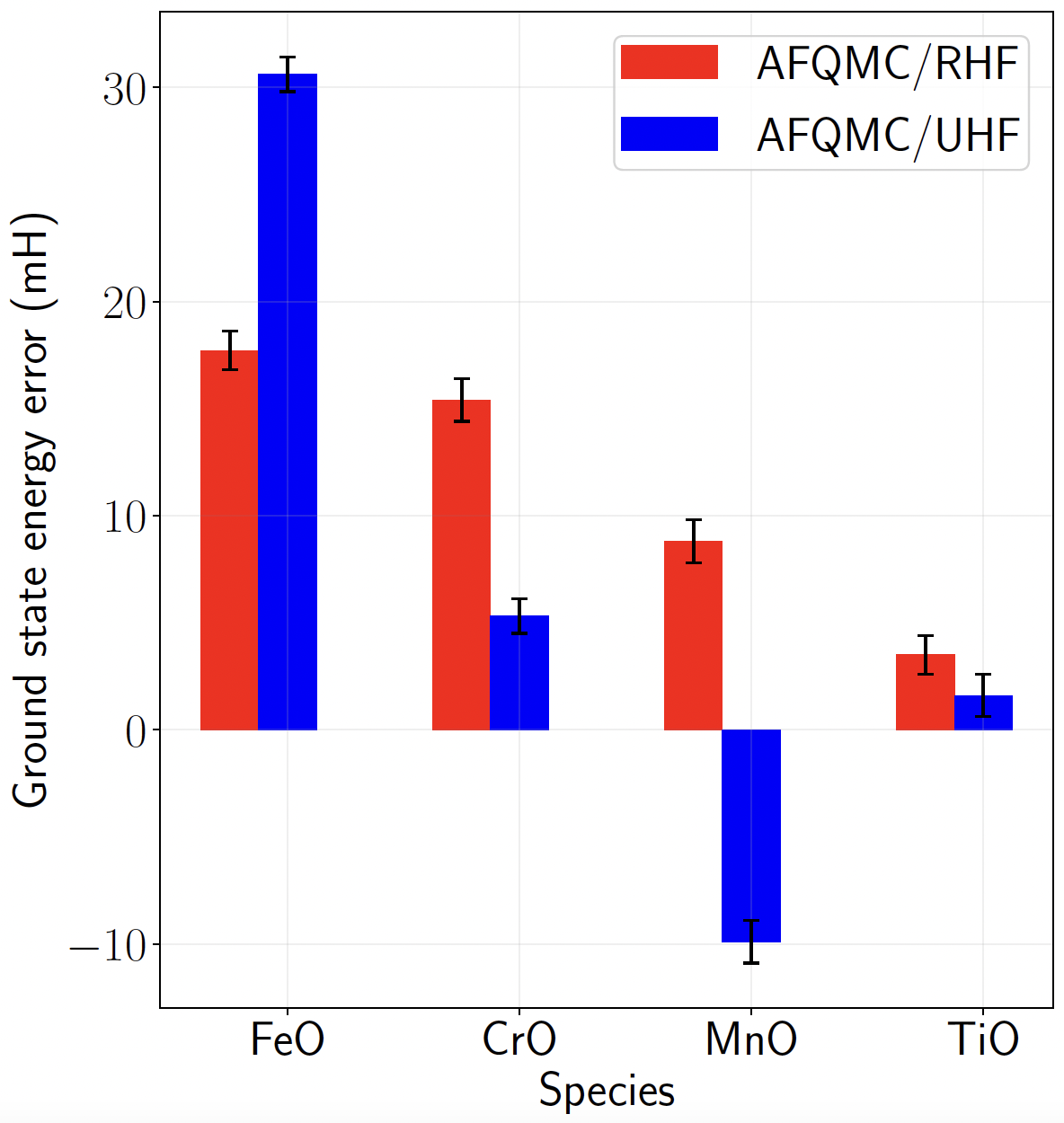
Single determinant AFQMC is (surprisingly) accurate in many cases
It does struggle sometimes
Williams et al. PRX '20
AM, Lee, Sharma JCP '22
Transition metal oxide molecules (~20e, 76o)
Possible remedies
- Improve single determinant trial state self-consistently
Qin, Shi, Zhang PRB '16
- Correlated trial states: Jastrow, CCSD, MPS, ...
Hubbard-Stratonovich
Chang, Rubenstein, Morales PRB '16
AM, Sharma JCTC '21
Multideterminant states: selected configuration interaction
- Put the most important configurations in the state using particle-hole excitations and optimize
Selected configuration interaction
Heat bath CI can handle fairly large spaces, e.g. (28e, 198o) calculation for Cr2 reported in Li et al. PRR '20
- In real space QMC: reduced cost scaling due to the algorithm of Filippi, Assaraf, Moroni (JCP '16)
- In AFQMC: cost of single determinant trial local energy is O(N4). Can we avoid O(NdN4)?
Selected CI local energy algorithm
Generalized Wick's theorem: consider ∣ψT⟩=cptqua^t†a^pa^u†a^q∣ψ0⟩
AM, Sharma JCTC '21
AM, Lee, Sharma JCP '22
O(Nd+N5)
O(NNd+N4)
or
Benzene (30e, 102o)
H50 (50e, 50o)
AM, Lee, Sharma JCP '22
Choosing orbital spaces
Butadiene
States like open-shell singlet excited states cannot be expressed as single determinants
Choosing orbital spaces
1Ag→ 1Bu
(22e, 142o)
Going to the basis set limit: aTZ (22e, 318o)
AFQMC: 6.25(2) eV, Corrected experiment: 6.1 eV
[Cu2O2]2+ isomerization
ΔE=E(bis)−E(peroxo)
| Method | |
| DFT (UBLYP) | 36.0 |
| DFT (UB3LYP) | 52.9 |
| DFT (UMPW1K) | 74.0 |
| CCSD(T) | 30.6 |
| CR-CCSD(TQ) | 33.8 |
| DMRG-CT | 27.1 |
| ph-AFQMC (NOCI) | 32.1 |
| fp-AFQMC | 24.1(6) |
kcal/mol
AM, Sharma JCTC '21
Malone, AM, Spencer, Lee '22
Two parts
Selected CI trial states in AFQMC:
what are they good for and how to use them
with Sandeep Sharma, Joonho Lee, Jo Kurian
Response properties in AFQMC:
ground state properties using algorithmic differentiation
with Sandeep Sharma
Properties in AFQMC
- Mixed estimator:
- Backpropagation:
- Response formulation:
1. Analytical derivatives
2. Finite difference with correlated sampling: multiple calculations for different observables
Adjoint algorithmic differentitation
Inputs: integrals, random numbers,...
Output: AFQMC energy
Adjoint or reverse mode: cost scaling same as that of energy → RDM's at the cost of energy!
Sorella, Capriotti JCP '10; Song, Martinez, Neaton JCP '20; Zhang, Chan '22; ...
calculate gradients in the reverse sweep
Implementation details
- The JAX library implements derivatives of many linear algebra operations
- Memory bottleneck: checkpointing to trade memory for computational time
- Derivatives of trial states: for mean field trials, issues due to degenerate orbitals
for i=j
and ϵi=ϵj
Molecular dipole moments (TZ basis)
https://github.com/sanshar/Dice
https://github.com/linusjoonho/ipie
https://github.com/QMCPACK/qmcpack
Future directions
- Applications to multiple-center transition metal compounds
- Condensed phase ab initio calculations
- Forces, phonon couplings from adjoint AD
- Use in embedding theories like DMET