Variantes del
Max-Mean
Dispersión
para el problema de
4 - 6 Feb MAEB 2015
An Thanh Pham | Rubén Carrasco | Francisco Gortázar | Micael Gallego | Abraham Duarte
Introducción
Métodos previos
VNS
Experimentación
Conclusiones
Tabla de Contenidos
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Diversidad Max-Mean (MMDP)
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Diversidad Max-Mean (MMDP)
Variantes del VNS para el problema de Dispersión Max-Mean
- La definición de distancia puede ser específica del problema
- La distancia entre dos elementos puede tomar valores negativos
- El tamaño de las soluciones es variable
- En este trabajo proponemos diferentes variantes del VNS para la búsqueda de soluciones aproximadas a este problema de optimización
Introducción
Ejemplo MMDP
Variantes del VNS para el problema de Dispersión Max-Mean
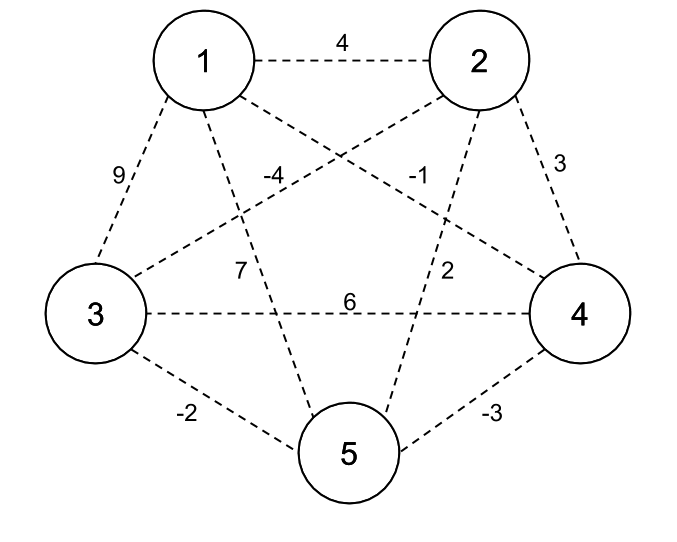
Introducción
Ejemplo MMDP
Variantes del VNS para el problema de Dispersión Max-Mean
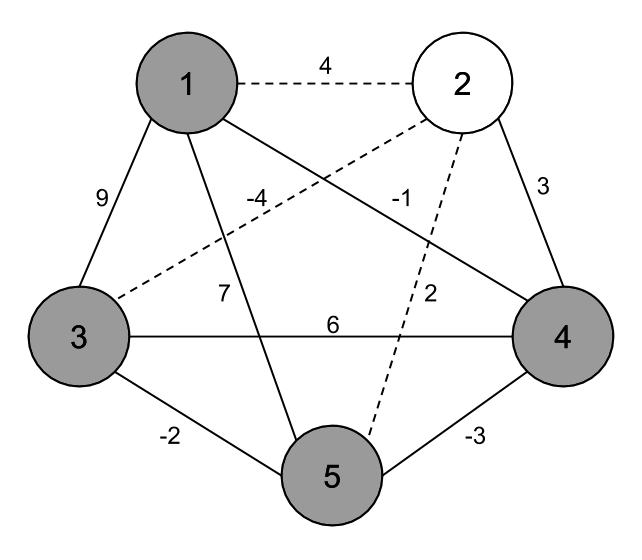
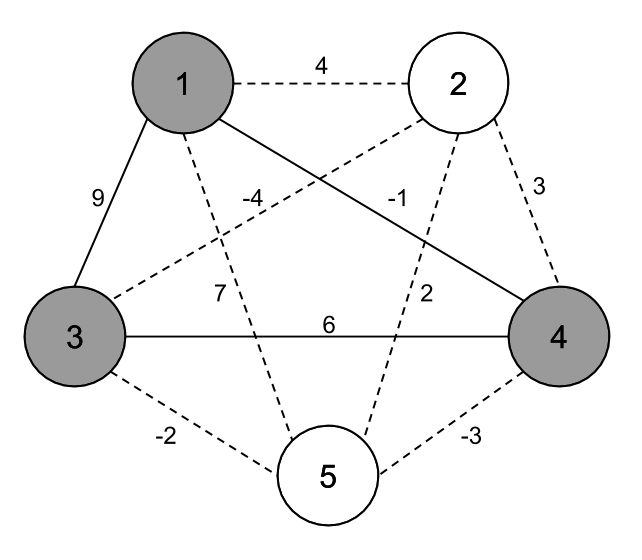
Introducción
Ejemplo MMDP
Variantes del VNS para el problema de Dispersión Max-Mean


Introducción
Métodos previos
VNS
Experimentación
Conclusiones
Tabla de Contenidos
Variantes del VNS para el problema de Dispersión Max-Mean
Métodos Previos
[Martí 13]
Variantes del VNS para el problema de Dispersión Max-Mean
Propone un GRASP especializado con Path Relinking para el problema del EDP
[Prokopyev 09]
Se presenta el problema del Equitable Dispersion Problem (EDP) y propone un método GRASP
Introducción
Métodos previos
VNS
Experimentación
Conclusiones
Tabla de Contenidos
Variantes del VNS para el problema de Dispersión Max-Mean
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Constructivos
Operadores de Vecindad
Búsqueda Local
Perturbación
Variantes
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
- Variantes y aplicaciones descritas por [Hansen 10]
- Tratan de escapar de los óptimos locales a través de cambios sistemáticos de los operadores de vecindad
- Propuesta por primera vez por [Mladenovic 97]
- Habitualmente compuesto por dos fases, búsqueda local, y perturbación de la solución
Introducción
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Constructivos
Operadores de Vecindad
Búsqueda Local
Perturbación
Variantes
VNS
Constructivo
Variantes del VNS para el problema de Dispersión Max-Mean
- Comienza con todos los elementos seleccionados
- Cada paso se elimina un elemento
- El algoritmo para cuando no hay ningún elemento que al eliminarlo, mejore el valor de la función objetivo
- El elemento eliminado es aquel que menos aporta a la función objetivo
VNS
Constructivo
Variantes del VNS para el problema de Dispersión Max-Mean
- Comienza sin ningún elemento seleccionado
- Cada paso se selecciona un elemento
- El algoritmo para cuando no hay ningún elemento que al seleccionarlo, mejore el valor de la función objetivo
- El elemento seleccionado es aquel que más aportaría a la función objetivo
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Constructivos
Operadores de Vecindad
Búsqueda Local
Perturbación
Variantes
VNS
Operadores de vecindad
Variantes del VNS para el problema de Dispersión Max-Mean
Intercambios
Insercciones
Borrados
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Constructivos
Operadores de Vecindad
Búsqueda Local
Perturbación
Variantes
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
- Probar todos los movimientos posibles empezando por los más prometedores
- La estrategia de selección es First-Improvement
- La búsqueda para cuando no hay movimiento que la mejore
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
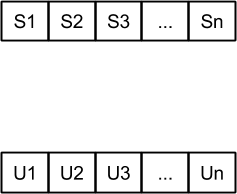
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
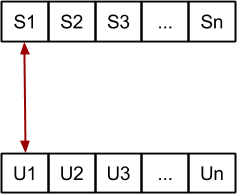
Probamos todos los intercambios entre S1 y Un
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
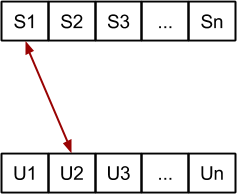
Probamos todos los intercambios entre S1 y Un
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
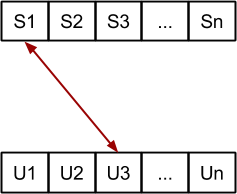
Probamos todos los intercambios entre S1 y Un
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
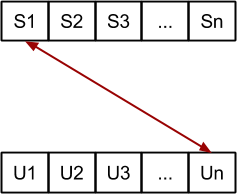
Probamos todos los intercambios entre S1 y Un
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
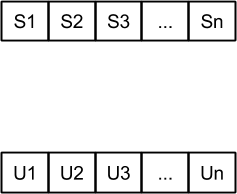
X
Probamos el borrado
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
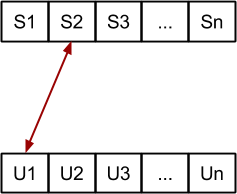
Probamos los intercambios con el siguiente elemento
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
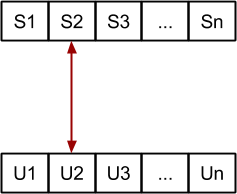
Probamos los intercambios con el siguiente elemento
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
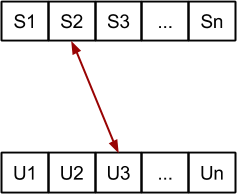
Probamos los intercambios con el siguiente elemento
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
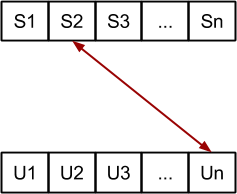
Probamos los intercambios con el siguiente elemento
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
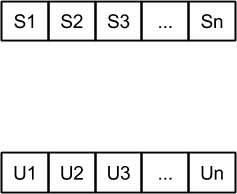
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
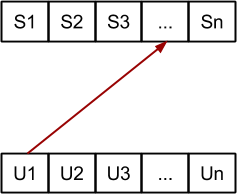
Probamos las insercciones
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
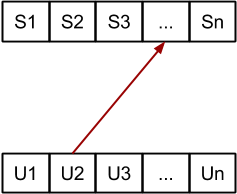
Probamos las insercciones
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
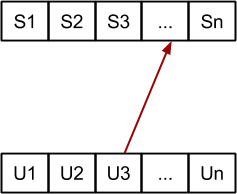
Probamos las insercciones
VNS
Búsqueda local
Variantes del VNS para el problema de Dispersión Max-Mean
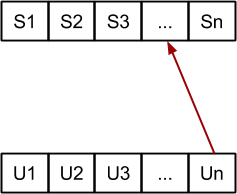
Probamos las insercciones
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Constructivos
Operadores de Vecindad
Búsqueda Local
Perturbación
Variantes
VNS
Mecanismo de perturbación
Variantes del VNS para el problema de Dispersión Max-Mean
- Perturbación en base al parámetro
- Una perturbación de tamaño consiste en intercambiar elementos seleccionados de forma aleatoria
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Constructivos
Operadores de Vecindad
Búsqueda Local
Perturbación
Variantes
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Variantes
Basic VNS (BVNS)
Variable Neighbourhood Descent (VND)
General VNS (GVNS)
VNS
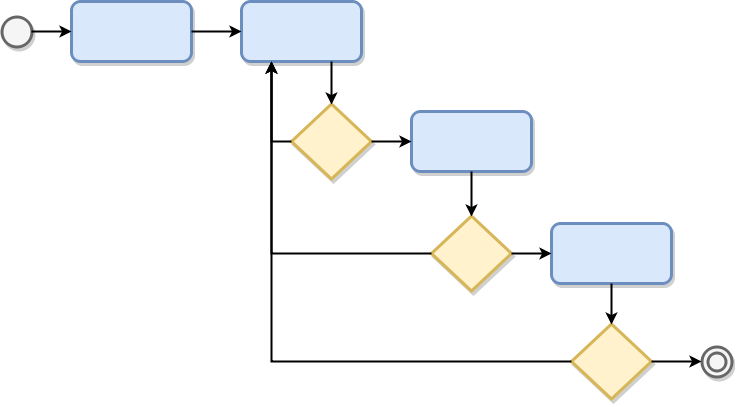
Variante BVNS
Variantes del VNS para el problema de Dispersión Max-Mean
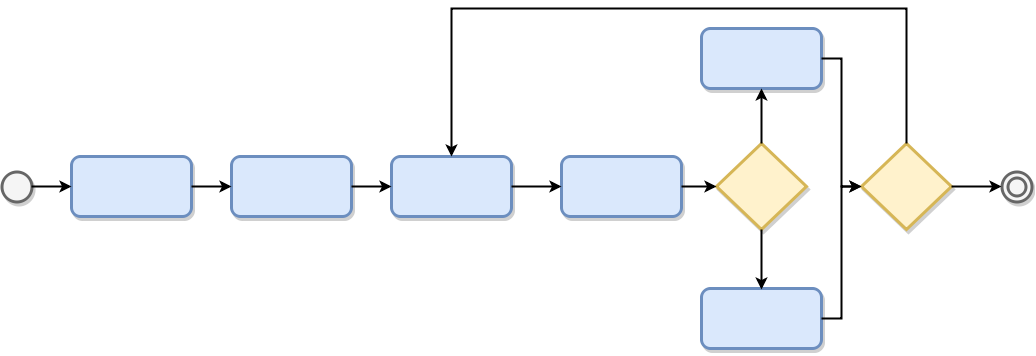
Constructivo
Perturbación
¿mejora?
Sí
No
Sí
No
VNS
Variantes del VNS para el problema de Dispersión Max-Mean
Constructivo
¿mejora?
Sí
No
Sí
No
Variante VND
¿mejora?
¿mejora?
No
Sí
VNS
Variante GVNS
Variantes del VNS para el problema de Dispersión Max-Mean
- Se sustituye por
- El mismo esquema algorítmico que BVNS
Introducción
Métodos previos
VNS
Experimentación
Conclusiones
Tabla de Contenidos
Variantes del VNS para el problema de Dispersión Max-Mean
Experimentación
Tipo I: Matrices simétricas de números reales entre [-10, 10] generados aleatoriamente con distribución uniforme
Instancias
Variantes del VNS para el problema de Dispersión Max-Mean
Tipo II: Matrices simétricas de números reales entre [-10, -5] U [5, 10] generados aleatoriamente con distribución uniforme
La generación de instancias viene dada por el estado del arte
Experimentación
Experimentos preliminares con 12 instancias
6 instancias de cada tipo
3 instancias de 150 y 3 de 500 por tipo
Experimento final con 40 instancias
20 instancias de cada tipo
10 instancias de 150 y 10 instancias de 500 por tipo
Fases
Variantes del VNS para el problema de Dispersión Max-Mean
Experimentación
Entorno
Variantes del VNS para el problema de Dispersión Max-Mean
- Intel i7 QuadCore 6GB RAM
- Algoritmos implementados con Java7
Experimentación
Selección del constructivo
| Método | DEV | #BEST | CPU TIME |
|---|---|---|---|
| [Martí 13] | 0.00% | 12 | 382.88 |
| 13.12% | 0 | 0.03 | |
| 4.82% | 0 | 0.01 |
Variantes del VNS para el problema de Dispersión Max-Mean
DEV = Desviación media respecto al mejor método del experimento
#BEST = Número instancias donde el método obtiene la mejor solución
CPU TIME = Tiempo de ejecución empleado por el método en segundos
Experimentación
Ajuste paramétrico del BVNS
| Método | DEV | #BEST | CPU TIME |
|---|---|---|---|
| [Martí 13] | 0.95% | 2 | 382.88 |
| BVNS | 2.00% | 0 | 2.31 |
| BVNS | 1.55% | 1 | 6.09 |
| BVNS | 1.26% | 2 | 15.73 |
| BVNS | 0.04% | 10 | 139.19 |
Variantes del VNS para el problema de Dispersión Max-Mean
Experimentación
Ajuste paramétrico del VND
| Método | DEV | #BEST | CPU TIME |
|---|---|---|---|
| [Martí 13] | 0.17% | 9 | 382.88 |
| VND | 1.68% | 1 | 2.93 |
| VND | 1.90% | 1 | 0.26 |
| VND | 1.30% | 1 | 0.84 |
| VND | 1.18% | 1 | 0.83 |
| VND | 1.40% | 1 | 0.25 |
| VND | 1.19% | 1 | 0.62 |
| VND | 1.97% | 0 | 0.04 |
Variantes del VNS para el problema de Dispersión Max-Mean
Experimentación
Ajuste paramétrico del GVNS
| Método | DEV | #BEST | CPU TIME |
|---|---|---|---|
| [Martí 13] | 0.78% | 2 | 382.88 |
| GVNS | 1.57% | 2 | 4.06 |
| GVNS | 1.10% | 2 | 2.13 |
| GVNS | 0.38% | 6 | 48.56 |
| GVNS | 0.03% | 10 | 80.40 |
Variantes del VNS para el problema de Dispersión Max-Mean
Experimentación
Comparativa Final
| Método | DEV | #BEST | CPU TIME |
|---|---|---|---|
| [Martí 13] | 0.89% | 6 | 382.88 |
| BVNS | 0.05% | 31 | 44.36 |
| GVNS | 1.56% | 3 | 225.22 |
| VND | 2.99% | 1 | 2.04 |
Variantes del VNS para el problema de Dispersión Max-Mean
Introducción
Métodos previos
VNS
Experimentación
Conclusiones
Tabla de Contenidos
Variantes del VNS para el problema de Dispersión Max-Mean
Conclusiones
- Se ha diseñado un método que mejora al estado del arte para las instancias propuestas.
Variantes del VNS para el problema de Dispersión Max-Mean
- Implementación y comparativa de diferentes variantes del VNS
- Se ha diseñado diferentes tipos de constructivos y vecindades
- En BVNS y GVNS, a mayor valor de , mejores resultados pero con mayor tiempo de ejecución
- El GNVS no es capaz de mejorar al BVNS aunque sea más elaborado
Variantes del
Max-Mean
Dispersión
para el problema de
4 - 6 Feb MAEB 2015
An Thanh Pham | Rubén Carrasco | Francisco Gortázar | Micael Gallego | Abraham Duarte