Diffeomorphic image registration taking topological differences into account
Metamorphosis on brain MRI containing Glioblastoma
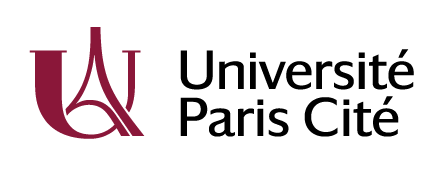



Anton François
Supervised by
Joan Glaunès & Pietro Gori




Introduction
Metamorphosis
Constrained Metamorphosis
Segmentation with TDA
Introduction

Anton François - 23/05/2023

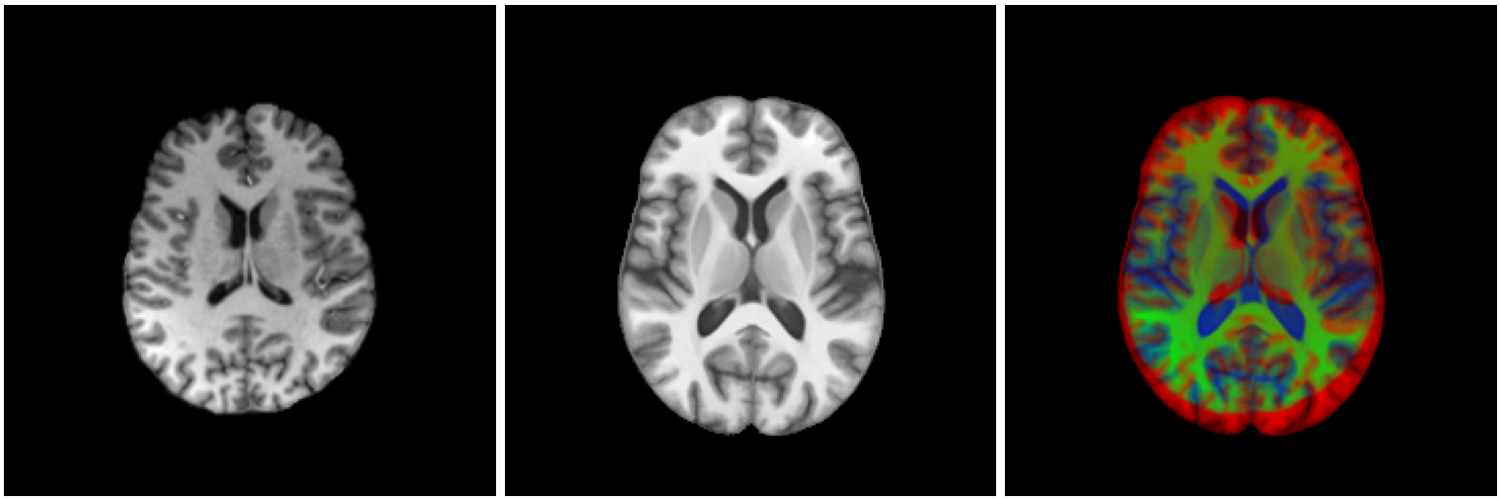










Image registration of medical images is an important step in many medical applications:
- pre/post-surgical operation
- multi-modality image fusion
- longitudinal studies
- statistical analysis (atlas construction)
Before
linear registration:
After
Image registration
Anton François - 23/05/2023












Diffeomorphic image registration:
Finding a smooth one-to-one (non-linear) deformation to be biologically plausible (no holes, shearing, tearing...)
But works only with healthy images...
Image registration











Anton François - 23/05/2023

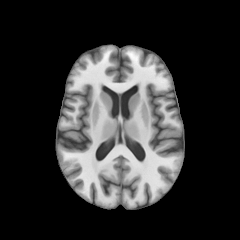
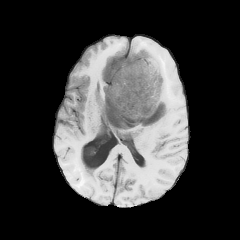
Registration with topological changes
Healthy brain
Brain with a glioblastoma

Anton François - 23/05/2023
Glioma registration problem

- Necrosis : topological difference
- Mass effect : morphological difference
- Oedema : appearance difference
- Brain natural differences
MNI template
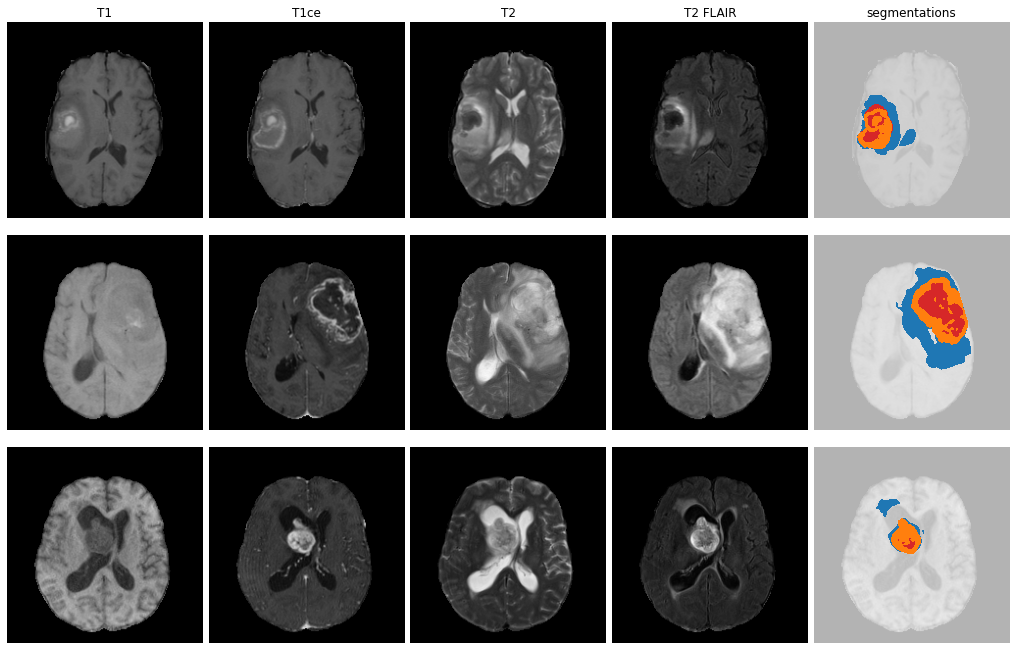



ET - GD enhancing tumour
ED - Peritumoural edematous/invaded tisue
NRC - Necrotic Tumour Core











Anton François - 23/05/2023
State of the art










For glioma registration:
- Cost-Function Masking (CFM) [Brett et al., 2001]
- Inpainting method [Sdika and Pelletier, 2009]
- Geometric Metamorphosis [Niethammer et al., 2012]
- GLISTR: biophysical models to perform registration. [Gooya et al., 2011; Ali et al., 2012]
- Deep-Learning: [Bône et al., 2020; Han et al., 2020b; Shu and et al, 2018; Wang et al., 2023]
LDDMM [Avants et al., 2008; Beg et al., 2005; Zhang and Fletcher, 2018] &
Metamorphosis [Holm et al., 2009; Trouvé and Younes, 2005]
We will base our registration on the methods:

Anton François - 23/05/2023


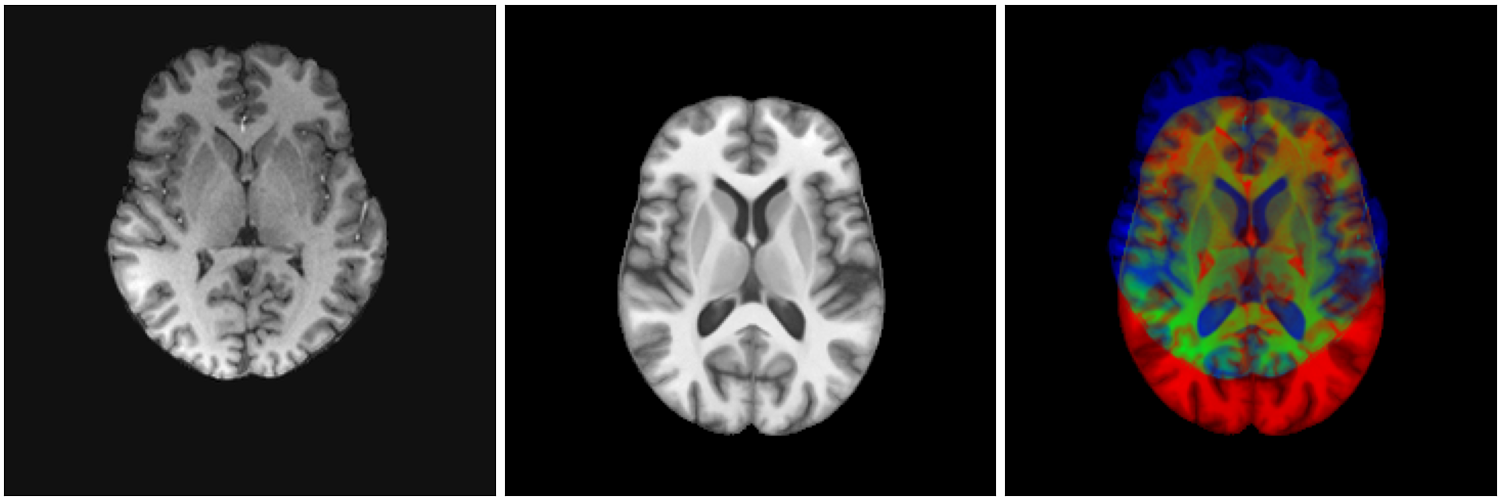
Source
Target
Automatic non-linear
matching
With modern methods










LDDMM

Anton François - 23/05/2023


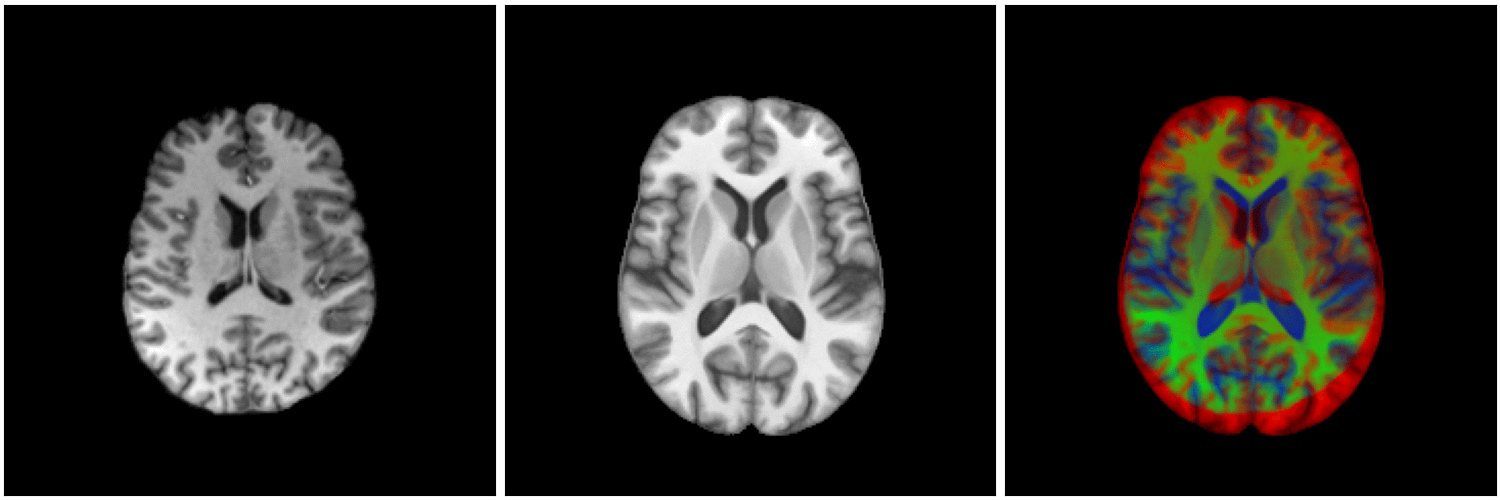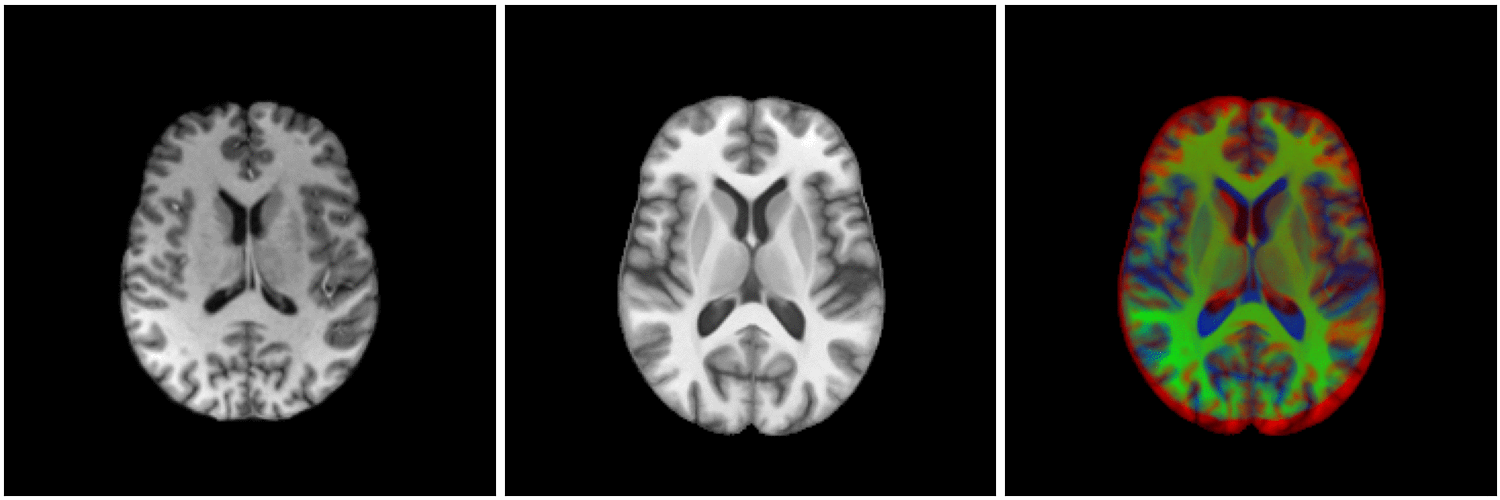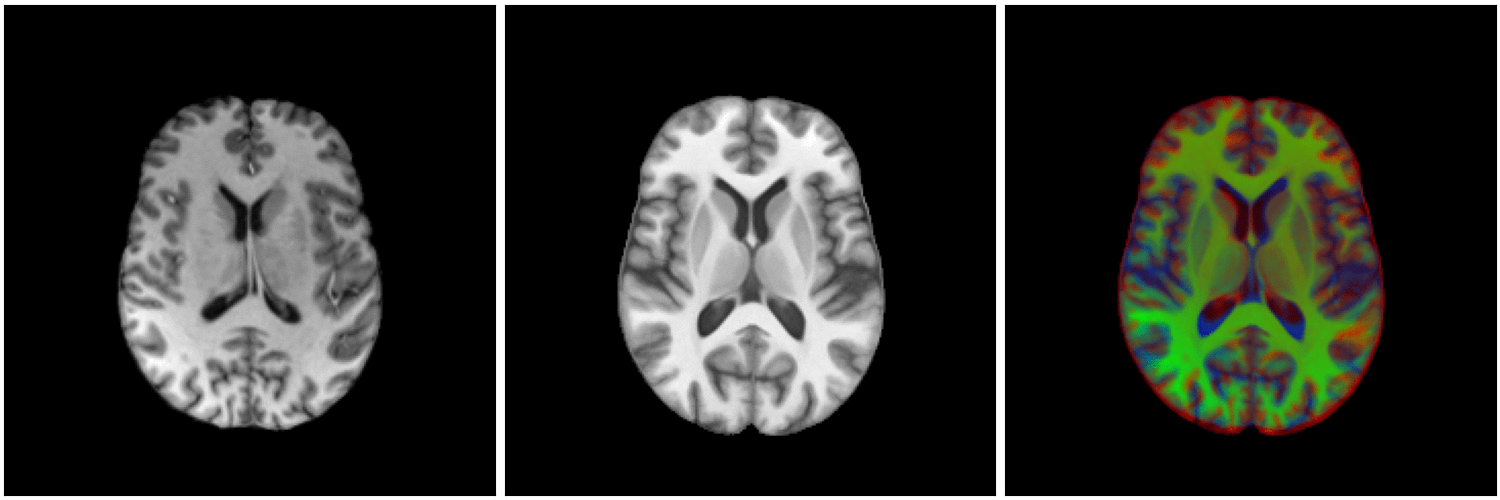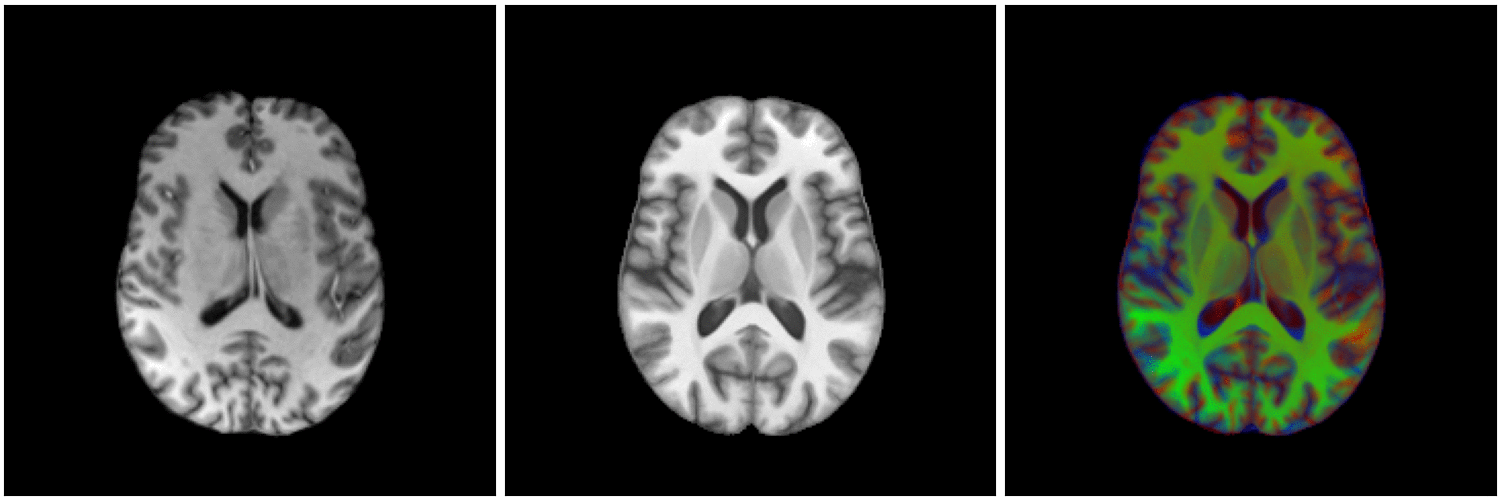
Source
Target
Automatic non-linear
matching
LDDMM: Large Diffeomorphic Deformation Metric Mapping
With modern methods











Anton François - 23/05/2023
Let \(V\) be the Reproducing Kernel Hilbert Space (RKHS) of vector fields whose kernel is \(K\). We denote \(L: V \rightarrow V^*\) the Riesz operator such that \(\|v\|^2_V = ( Lv,v)\) .
Let \(K\) be the Gaussian reproducing kernel with \[K(x,y) = \exp\left( -\frac{|x -y|^2}{2\sigma^2}\right) \cdot \mathrm{Id}_{\mathbb{R}^d}\]
V is an admissible RKHS of vector fields.
Deformation as a flow of vector field
\[\partial_t \varphi_t = v_t \circ \varphi_t\]










\(v_t \in V, \forall t\in [0,1]\)

Anton François - 23/05/2023


\(G\) is a group of diffeomorphisms
The deformation defined from the ordinary differential equation:
\[\partial_t \varphi_t = v_t \circ \varphi_t; \quad \varphi_0 = \mathrm{Id}\]
with \(v_t \in V,\forall t\in [0,1]\), is a diffeomorphism. We note \(\varphi^v \in G\) such a diffeomorphism.
\(G\) := Space of Deformations
Deformation as a flow of vector field











Anton François - 23/05/2023



\[\partial_t \varphi_t = v_t \circ \varphi_t; \quad \varphi_0 = \mathrm{Id}\]
Image transport (advection): \[\partial_t I_t = v_t \cdot \nabla I_t \]
Deformed image
\(I_t = I_0 \circ (\varphi^v)^{-1}\)
The deformation acts on images.










Geodesic := Shortest path for the exact matching:
\[\mathrm{inf}_v \int_0^1 \|v_t\|_V^2 dt\]

Anton François - 23/05/2023
LDDMM can reach only images with same topology
Metamorphosis deforms images and adds intensity.
Making the registration of images B and C possible.
\[\partial_t I_t = v_t \cdot \nabla I_t\]
\[+ \mu z_t\]
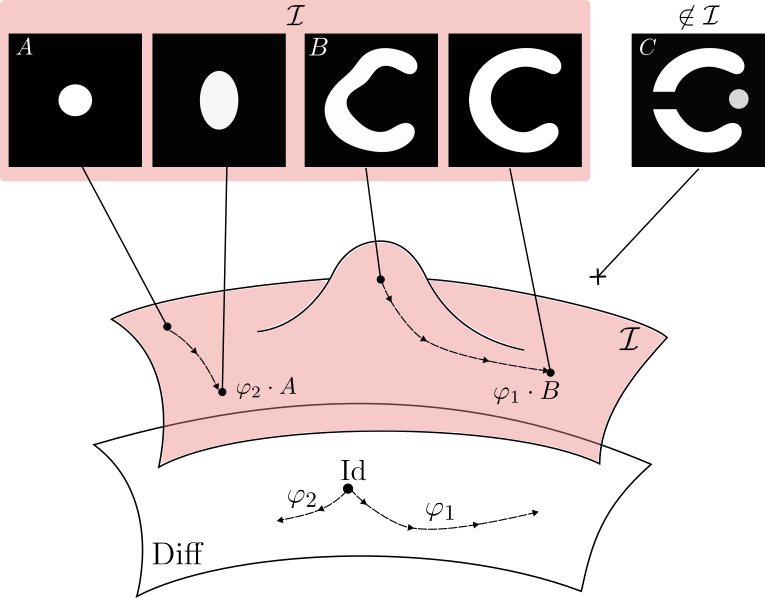
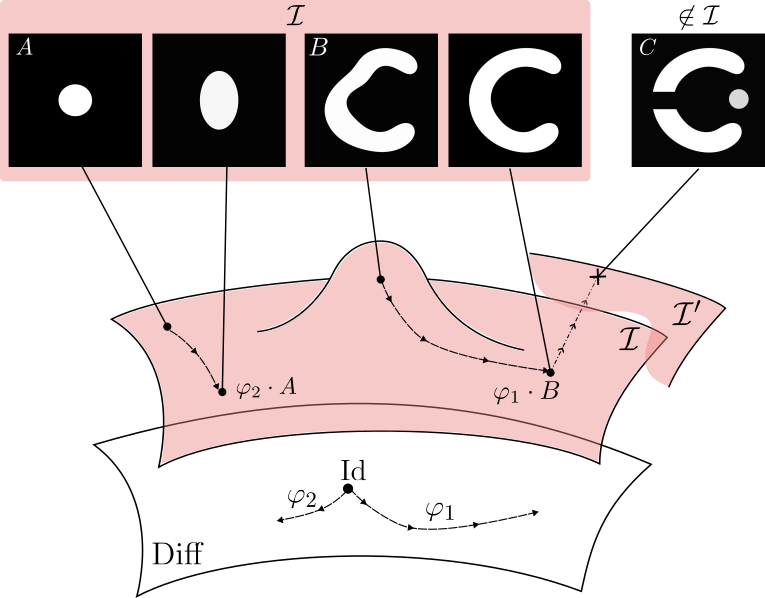
Topology and appearances variations










Metamorphosis
Implementation


Anton François - 23/05/2023









Metamorphosis
A Metamorphosis on \(\mathcal I\) is a pair of curves \((\varphi_t, \psi_t)\), respectively on \(G\) and \(\mathcal I\), with \(\varphi_0 = \mathrm{Id}\).
\(G\) := Space of Deformations
\(\mathcal I\) := Space of images
\(\psi_t\) is the intensity changes evolution part: \(I_t = \psi_t \circ (\varphi_t)^{-1}\)













Anton François - 23/05/2023









Metamorphosis
$$\left\{\begin{array}{rl}v_t &= -\frac{\rho}{\mu} K_\sigma \star (z_t \nabla I_t)\\ \dot z_t &= -\quad \nabla \cdot (z_t v_t) \\ \dot I_t &= -\langle v_t , \nabla I_t\rangle + \mu z_t\end{array}\right.$$
Advection equation with sourceContinuity equation

By computing the Euler-Lagrange equation of the exact matching cost :
and doing the variation with respect to \(I\) and \(v\) we obtain this set of geodesic equations:
[Trouvé & Younes, 2005]
$$ E_\mathrm M (I,v) = \frac12\int_0^1 \|v_t\|_V^2 + \rho \|z_t\|_{L_2}^2 dt \quad s.t.\ I_0 = S, I_1 = T$$












Anton François - 23/05/2023









Metamorphosis Optimisation
via Geodesic shooting
$$\left\{\begin{array}{rl}v_t &= -\frac{\rho}{\mu} K_\sigma \star (z_t \nabla I_t)\\ \partial_t z_t &= -\quad \nabla \cdot (z_t v_t) \\ \partial_t I_t &= -\langle v_t , \nabla I_t\rangle + \mu z_t\end{array}\right.$$
We minimize the inexact matching cost :
$$ H_\mathrm M (I,v) = \frac1 2 \left\| I_1 - T \right\|_2^2 + \frac \lambda 2\int_0^1 \|v_t\|_V^2 + \rho \|z_t\|_{L_2}^2 dt $$
Geodesic Integration
\(z_0\)
\(I_1\)
Step 1:
Step 2:
We iterate over two steps:












Anton François - 23/05/2023









We minimize this cost :
$$ H_\mathrm M (I,v) = \frac1 2 \left\| I_1 - T \right\|_2^2 + \frac \lambda 2\int_0^1 \|v_t\|_V^2 + \rho \|z_t\|_{L_2}^2 dt $$
$$ \Leftrightarrow H_\mathrm M (z_0) = \frac1 2 \left\| I_1 - T \right\|_2^2 + \frac \lambda 2\left( \|z_0\nabla I_0\|_V^2 + \rho \|z_0\|_{L_2}^2\right) $$
\(\nabla H_M\) and adjoint equations computed
with auto differentiation.

\(v_0 = - \frac \rho \mu K\star (z_0 \nabla I_0) \)
\(\|v_0\|_V+ \rho \|z_0\|_{L^2} = \|v_t\|_V +\rho \|z_t\|_{L^2} ,\forall t\in [0,1]\)
Metamorphosis Optimisation
via Geodesic shooting












Anton François - 23/05/2023
Lagrangian Formulation
$$x'(t) = v(t,x)$$
Lagrangian scheme
Not suitable for images
Eulerian scheme
\(I_{t+\delta_t} = I_t - \delta_t(v_t \times\nabla I_t)\)
Eulerian Formulation
$$\partial_t I(t,x) = - v(t,x) \cdot \nabla I(t,x)$$











Integration of the geodesics equations

Anton François - 23/05/2023









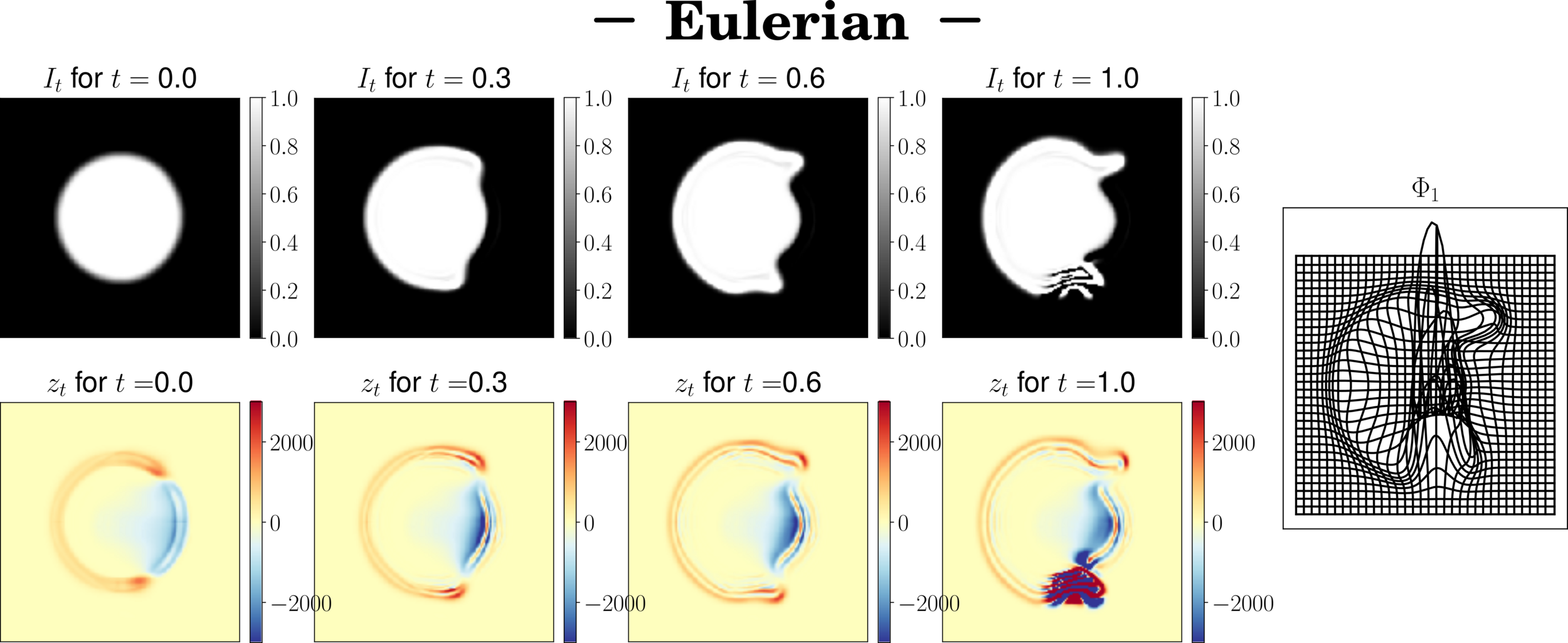
Schemes stability
Field aberations
We have to augment the number of time steps -> slow












Anton François - 23/05/2023
Semi-Lagrangian scheme principle
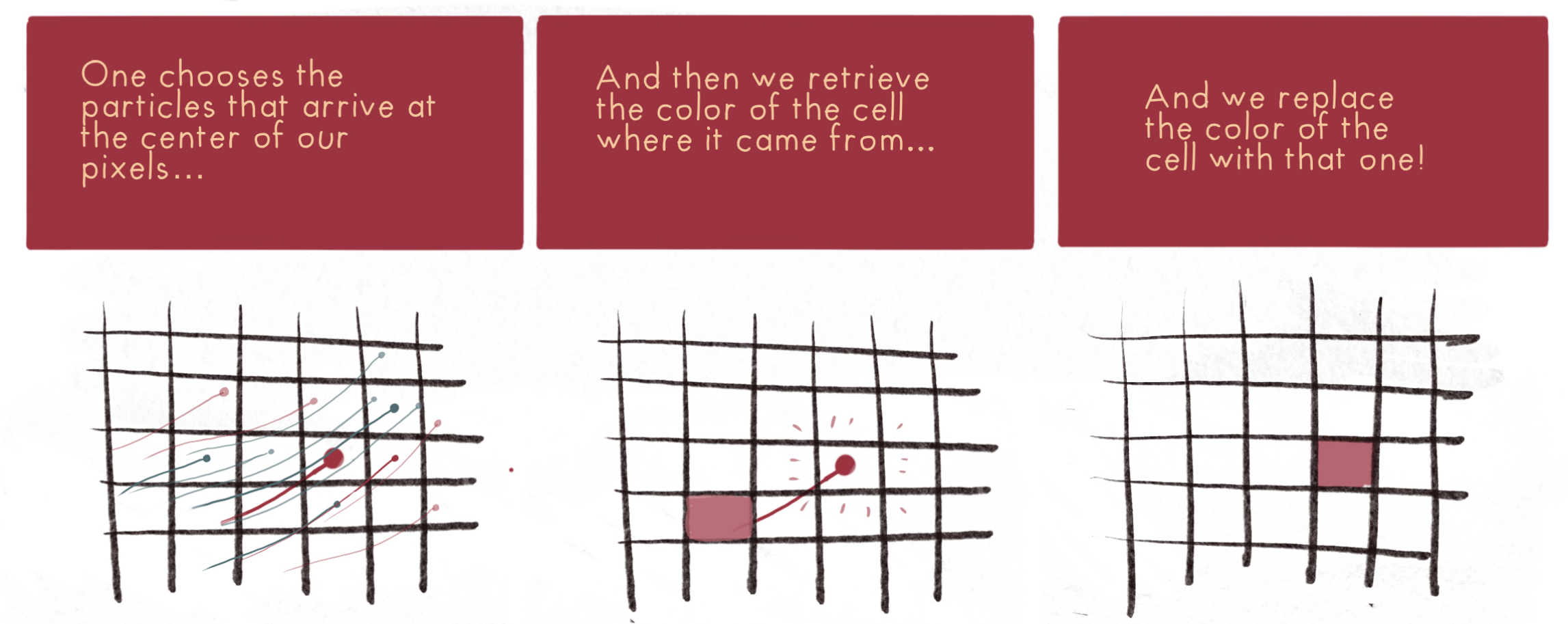
\(\partial_t I_t = v_t \cdot \nabla I_t + \mu z_t\)
Semi-Lagrangian scheme
\(I_{t+\delta_t} = \mathrm{Interp}(I_t,\varphi^{v_t}) + \delta_t \mu z_t\)












Anton François - 23/05/2023
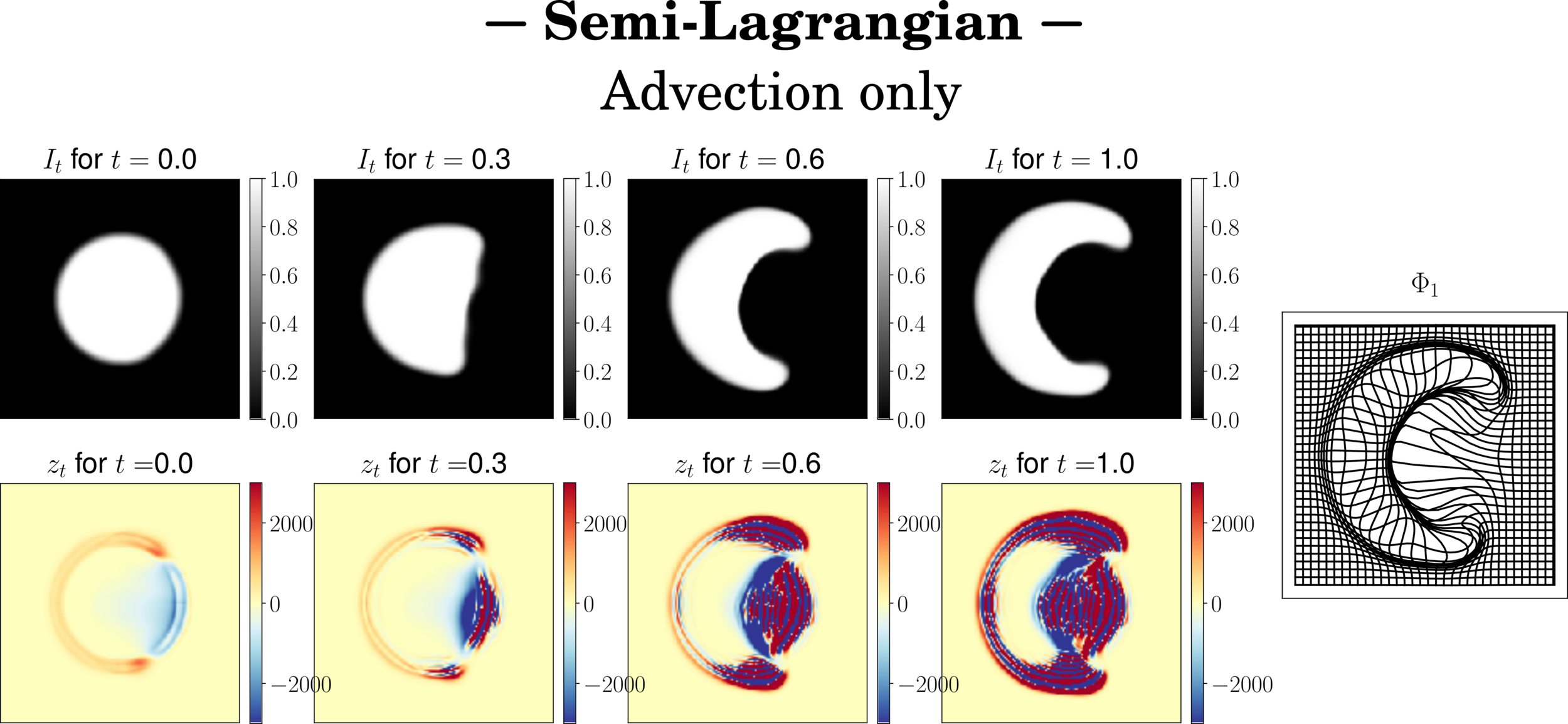
Schemes stability
Image integration more stable
residual instabilities












Anton François - 23/05/2023
Schemes stability
Stable image
Stable residual
Semi-Lagrangian scheme on residual
\(z_{t+\delta_t} = \mathrm{Interp}(z_t,\varphi^{v_t}) - \delta_t z_t \mathrm{div}(v_t)\)
\(\partial_t z_t = - \mathrm{div} (z_t v_t)\)
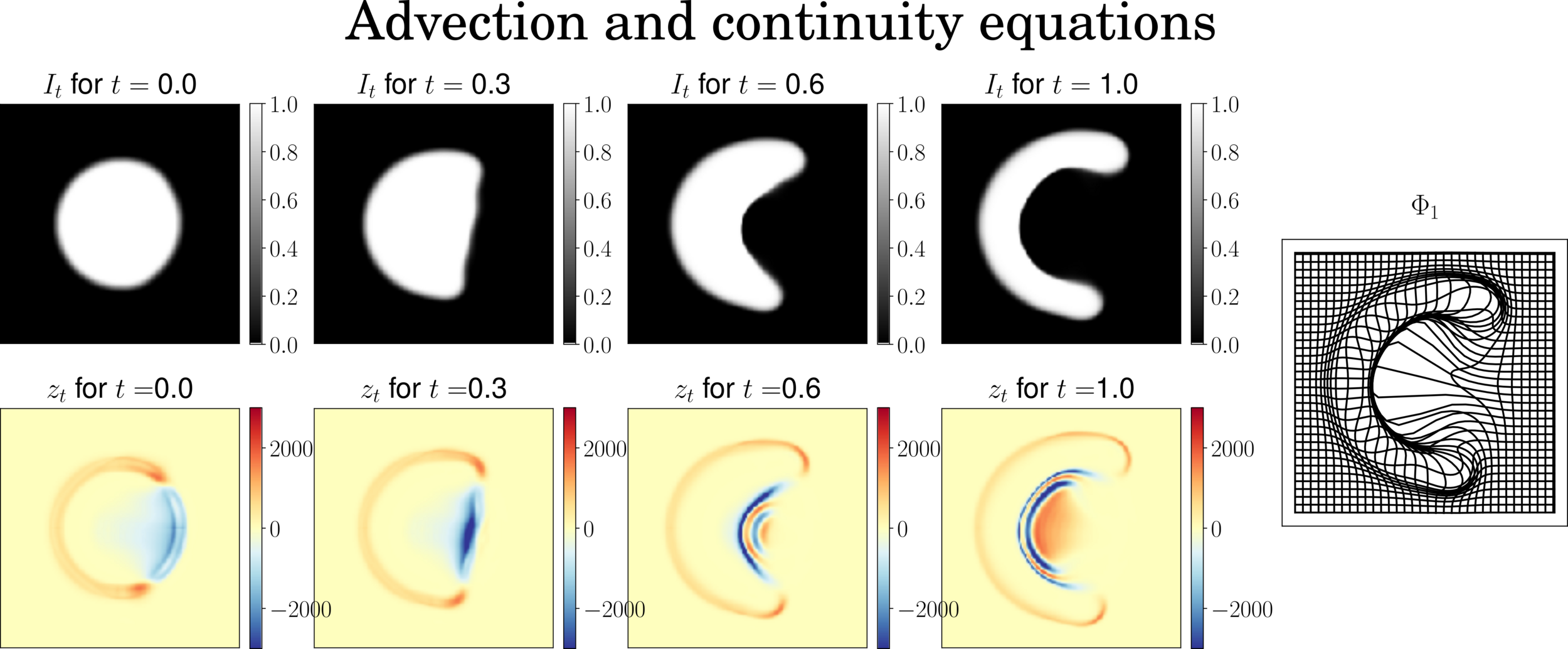
- Full semi-Lagrangian -












Anton François - 23/05/2023



github.com/antonfrancois/Demeter_metamorphosis
- The semi-Lagrangian scheme is more stable
- Open-Source Metamorphosis on the GPU, with autodiff.
- Made for prototyping












Anton François - 23/05/2023











Problem solved ?

\(\rho\) and \(\mu\) control ratio between intensity changes and deformation
small intensity changes
big intensity changes
Problem solved ?


small intensity changes
big intensity changes

NO !











Residual entanglement!
Constrained
Metamorphosis














Anton François - 23/05/2023
Weighted Metamorphosis
$$\left\{\begin{array}{rl}v_t &= -\frac{\rho}{\mu} K_\sigma \star (z_t \nabla I_t)\\ \dot z_t &= \quad - \nabla \cdot (z_t v_t) \\ \dot I_t &= - v_t \cdot \nabla I_t + \mu M_t z_t\end{array}\right.$$
Let \((M_t)_{t\in [0,1]}\) be a continuous temporal mask. By computing the Euler-Lagrange equation of the exact matching cost :
$$E_{\mathrm{WM}}(I,v) = \frac 12\int_0^1\|v_t\|_V^2 + \rho\langle z_t, M_t z_t \ \ \rangle_{L^2} dt \quad s.t.\ I_0 = S, I_1 = T $$
and doing the variation with respect to \(I\) and \(v\) we obtain this set of geodesic equations:
\(\langle z_t, M_t z_t \rangle_{L^2}\)
\(M_t\)













Anton François - 23/05/2023




Source
Target
LDDMM
Metamorphosis

WM
A static mask gets stuck













Anton François - 23/05/2023
Weighted Metamorphosis
with a growing mask.
1. We set \(M_1\) as the topological difference segmentation.
2. We initialise \(M_0\) as a small ball at its center.


3. We register \(M_0\) to \(M_1\) using LDDMM.

Simple and realistic prior modelling:













Anton François - 23/05/2023


Source
Target

WM

WM w. Growing mask

Weighted Metamorphosis
with a growing mask.













Anton François - 23/05/2023
With textured images,
no mass effect is produced
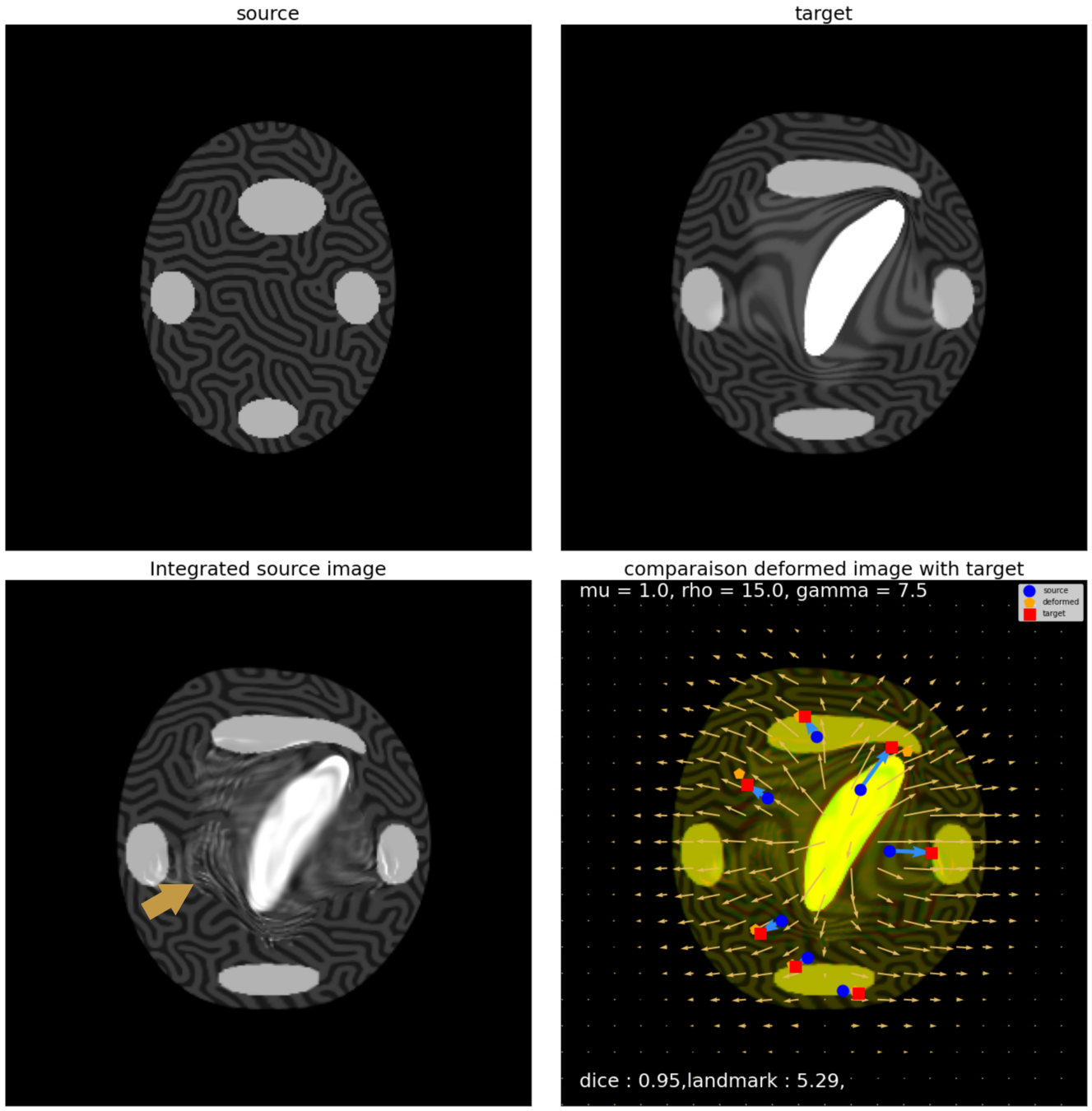
WM fails on more realistic images

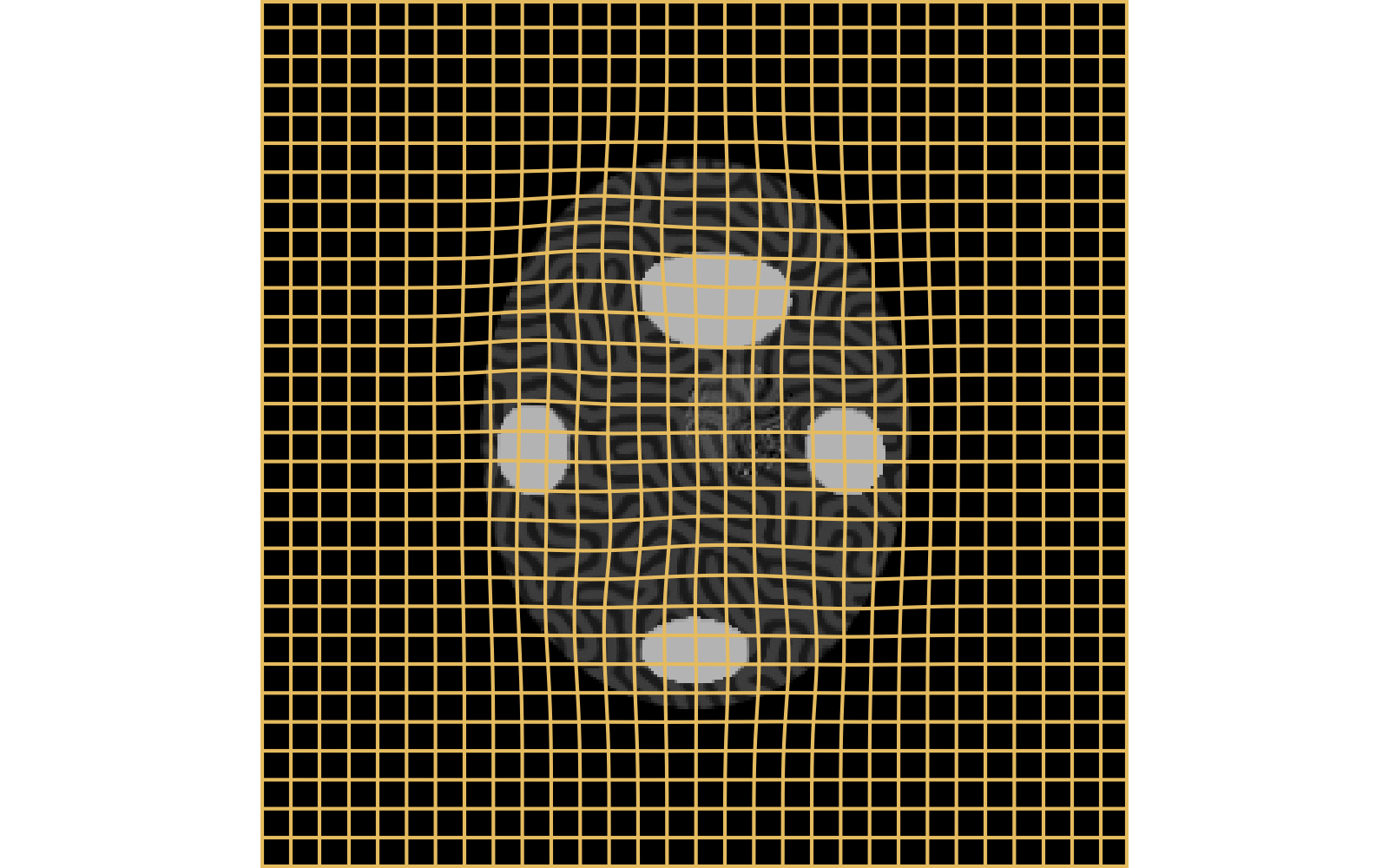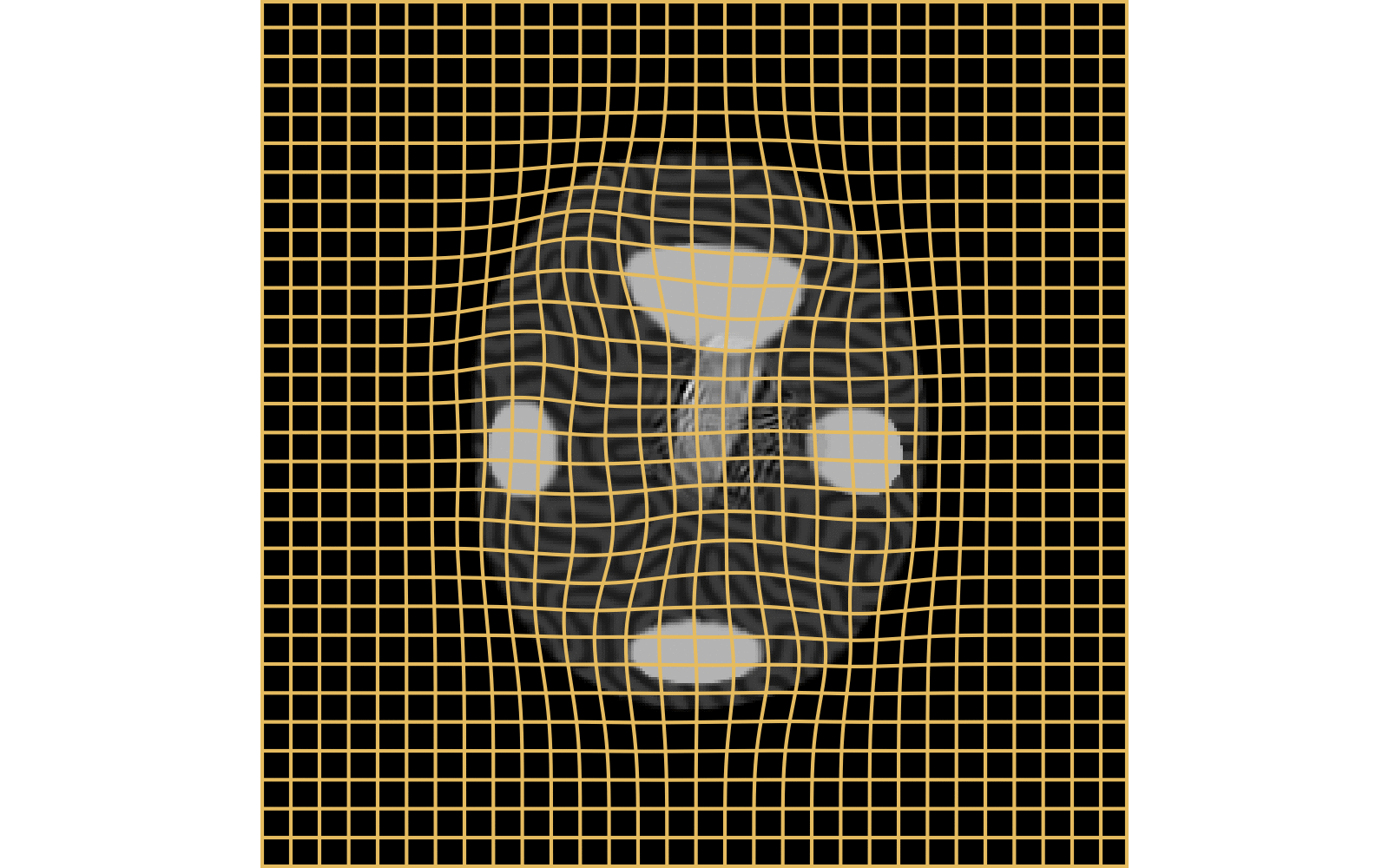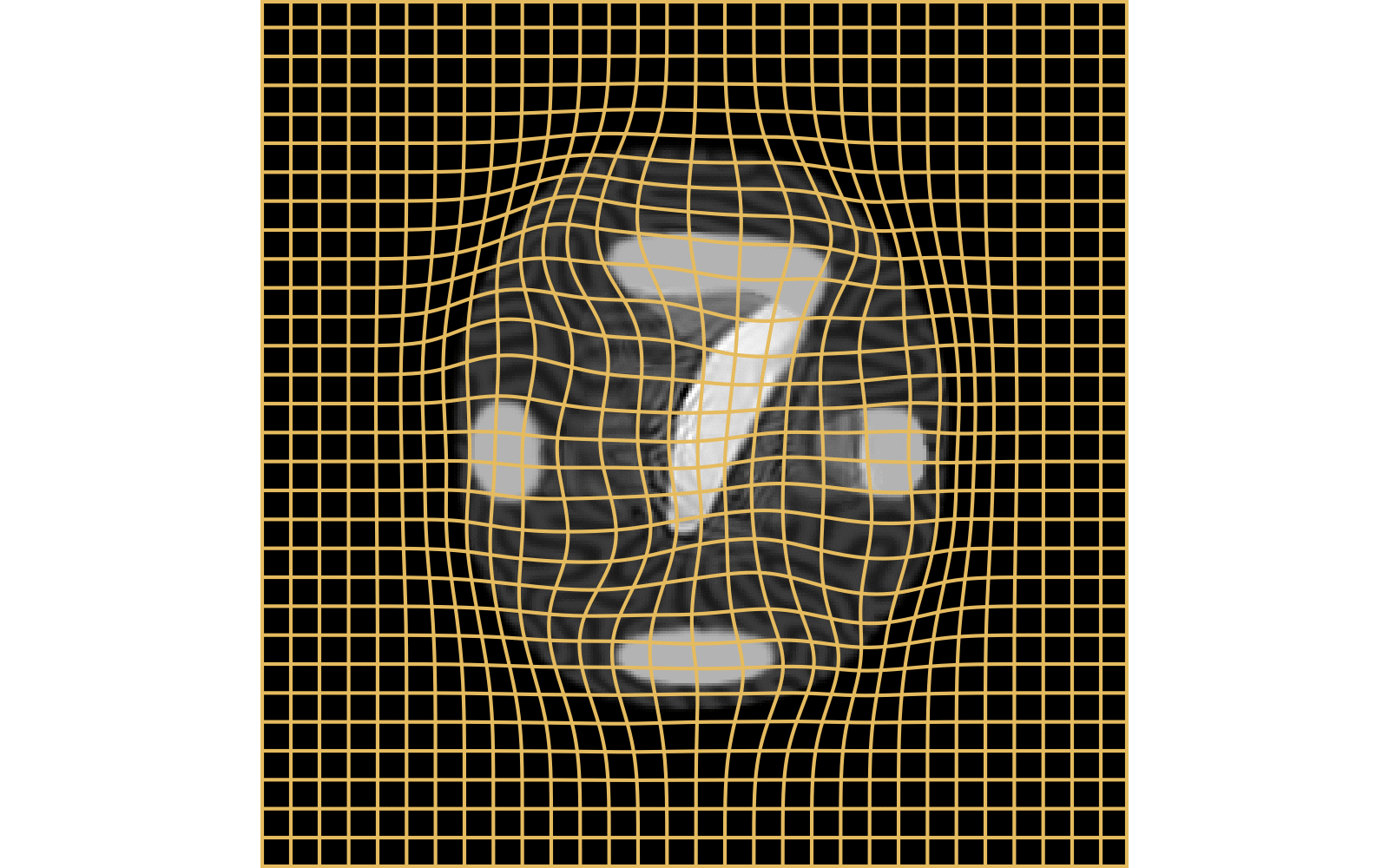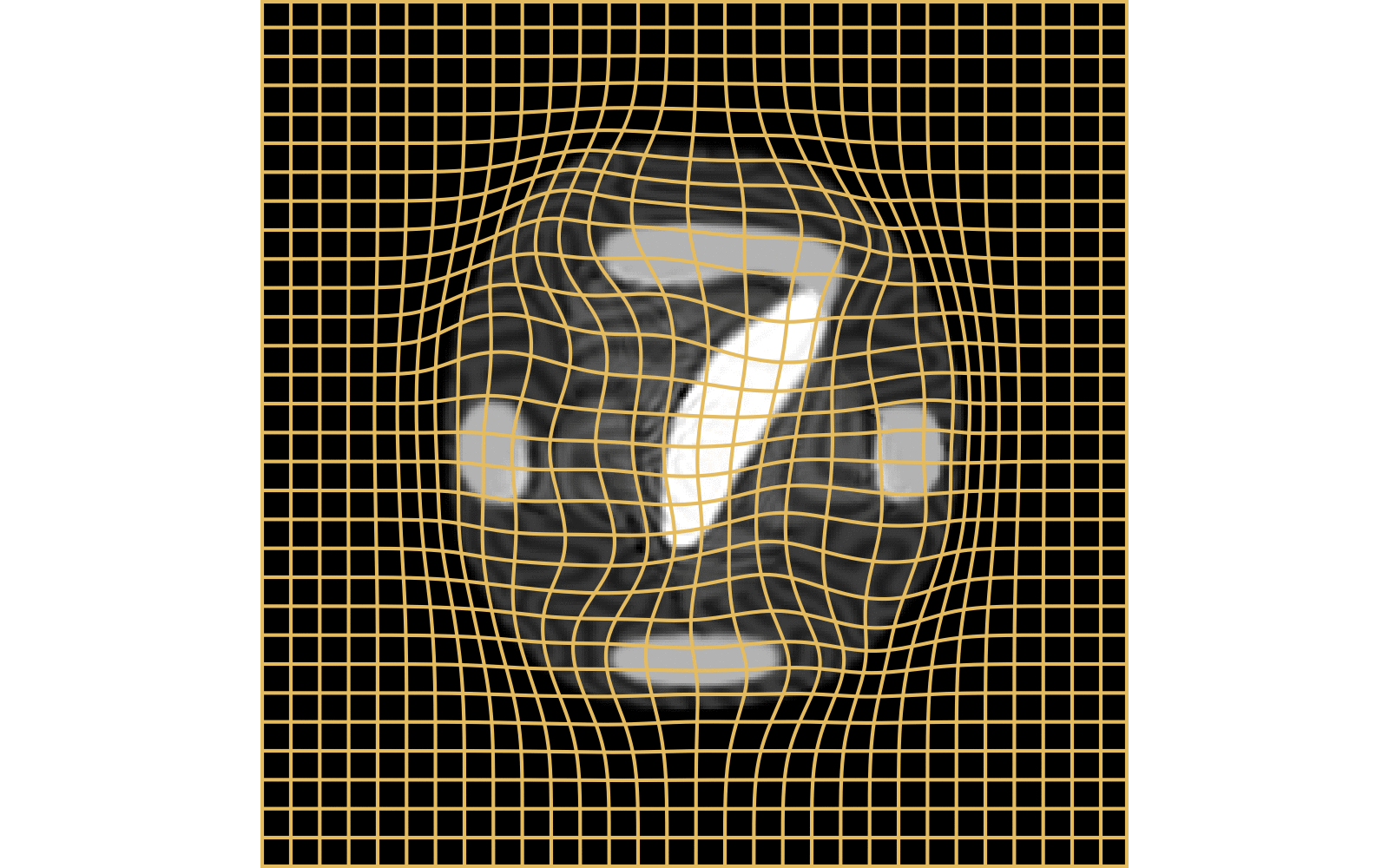













Anton François - 23/05/2023

\(M_t\) : Adding intensities
Oriented Metamorphosis
\(P_t\): Indicates where the vector field should be followed
\(w_t\): vector field to follow
We want to force the registration to follow the LDDMM field.













Anton François - 23/05/2023
Constrained Metamorphosis
Let \((M_t)_{t\in [0,1]}\) and \((P_t)_{t\in [0,1]}\) be two continuous temporal masks and \(w_t \in V\), an admissible vector field.
By computing the Euler-Lagrange equation of the exact matching cost:
$$ E_{\mathrm{CM}}(I,v) = \int_0^1 \|v_t\|_V^2 + \rho \langle z_t, M_t z_t \rangle_{L^2} +\gamma\| P_t(v_t - w_t) \|_V^2 dt $$
Oriented & Weighted
\(s.t., I_0 = S, I_1 = T\)
\[\| P_t(v_t - w_t) \|_V^2\]













Anton François - 23/05/2023
Constrained Metamorphosis
Let \((M_t)_{t\in [0,1]}\) and \((P_t)_{t\in [0,1]}\) be two continuous temporal masks and \(w_t \in V\), an admissible vector field.
By computing the Euler-Lagrange equation of the exact matching cost:
$$ E_{\mathrm{WM}}(I,v) = \int_0^1 \|v_t\|_V^2 + \rho \langle z_t, M_t z_t \rangle_{L^2} +\gamma\| P_t(v_t - w_t) \|_V^2 dt $$
Oriented & Weighted
\(s.t., I_0 = S, I_1 = T\)
\[\| P_t(v_t - w_t) \|_V^2\]
Oriented Norm:
We seak to estimate \(v_t\) similar to \(w_t\) where the mask \(P_t\) is positive.













Anton François - 23/05/2023
Constrained Metamorphosis
Let \((M_t)_{t\in [0,1]}\) and \((P_t)_{t\in [0,1]}\) be two continuous temporal masks and \(w_t \in V\), an admissible vector field.
By computing the Euler-Lagrange equation of the exact matching cost:
$$ E_{\mathrm{CM}}(I,v) = \int_0^1 \|v_t\|_V^2 + \rho \langle z_t, M_t z_t \rangle_{L^2} +\gamma\| P_t(v_t - w_t) \|_V^2 dt $$
and doing the variation with respect to \(I\) and \(v\) we obtain this set of geodesic equations:
Oriented & Weighted
\(s.t., I_0 = S, I_1 = T\)
Theorem:
$$\left\{\begin{array}{rl} v_t &= - \frac{\rho}{\mu (1 + \gamma P_t)} K \star (z_t\nabla I_t) + \frac{\gamma P_t }{1 + \gamma P_t} w_t\\ \dot z_t &= -\quad \nabla \cdot (z_t v_t) \\ \dot I_t &= - v_t , \cdot\nabla I_t + \mu M_t z_t\end{array}\right.$$
\(\frac{\rho}{\mu(1+\gamma P_t)}\)
\(\frac{\gamma P_t}{1+\gamma P_t}\)













Anton François - 23/05/2023

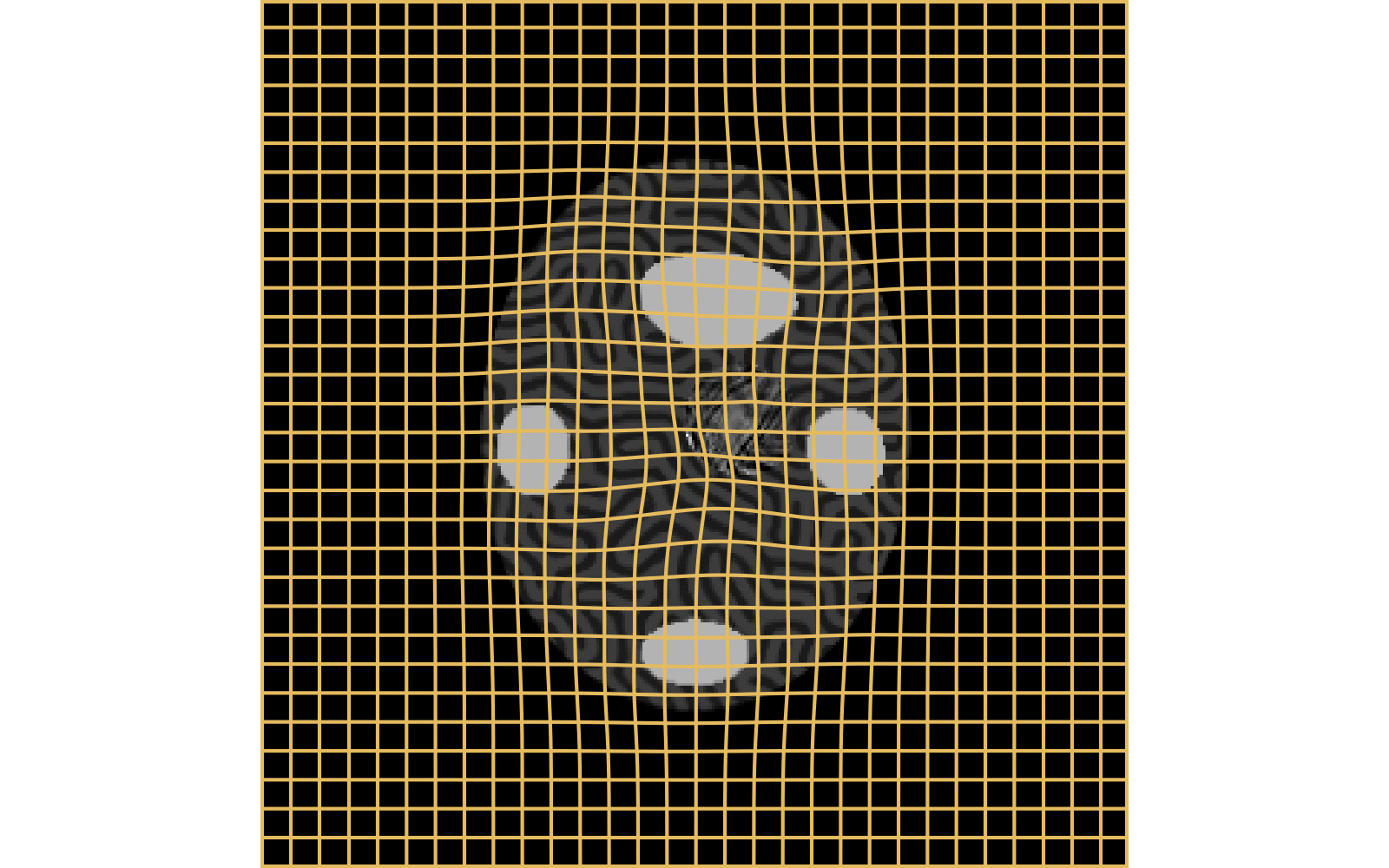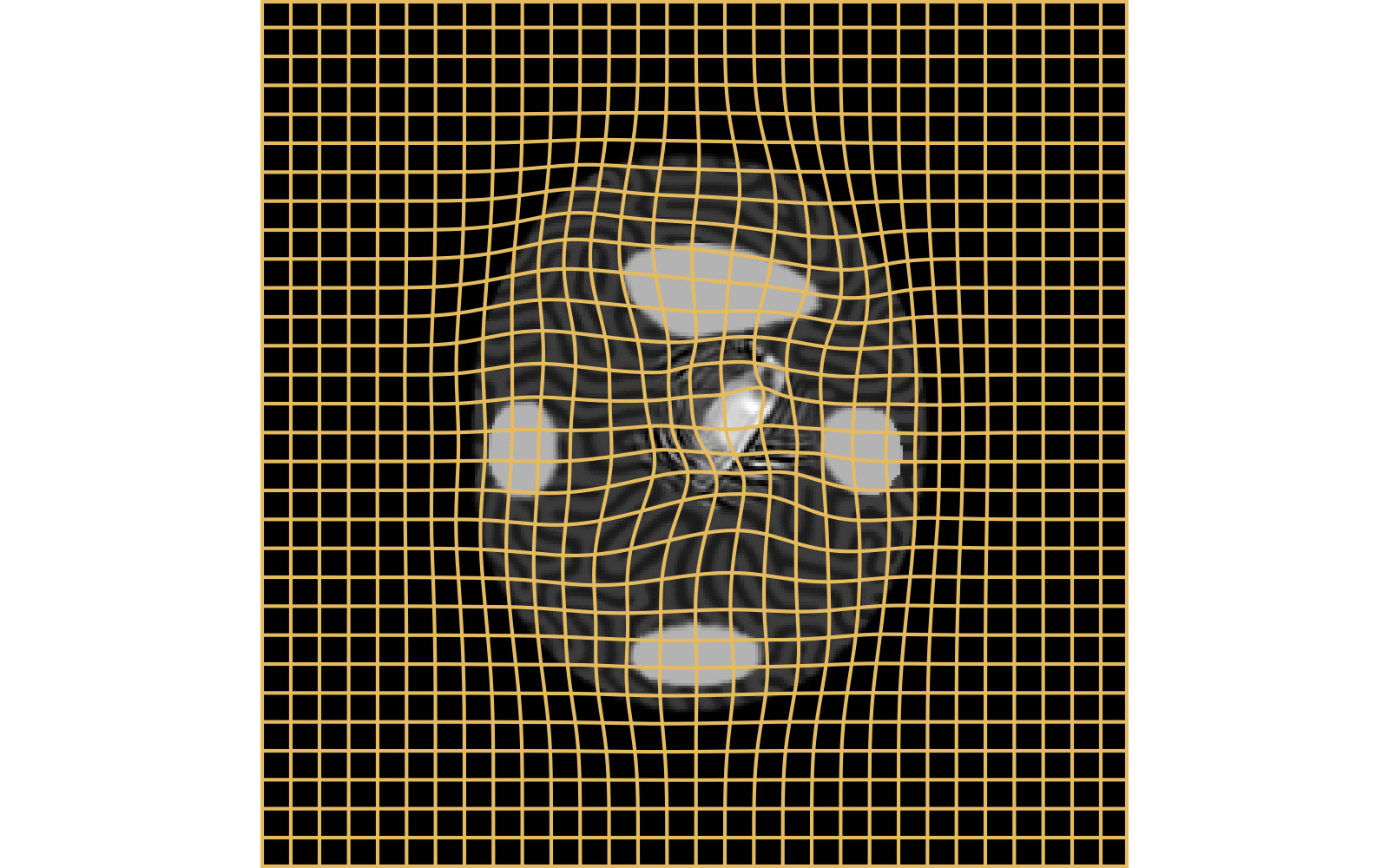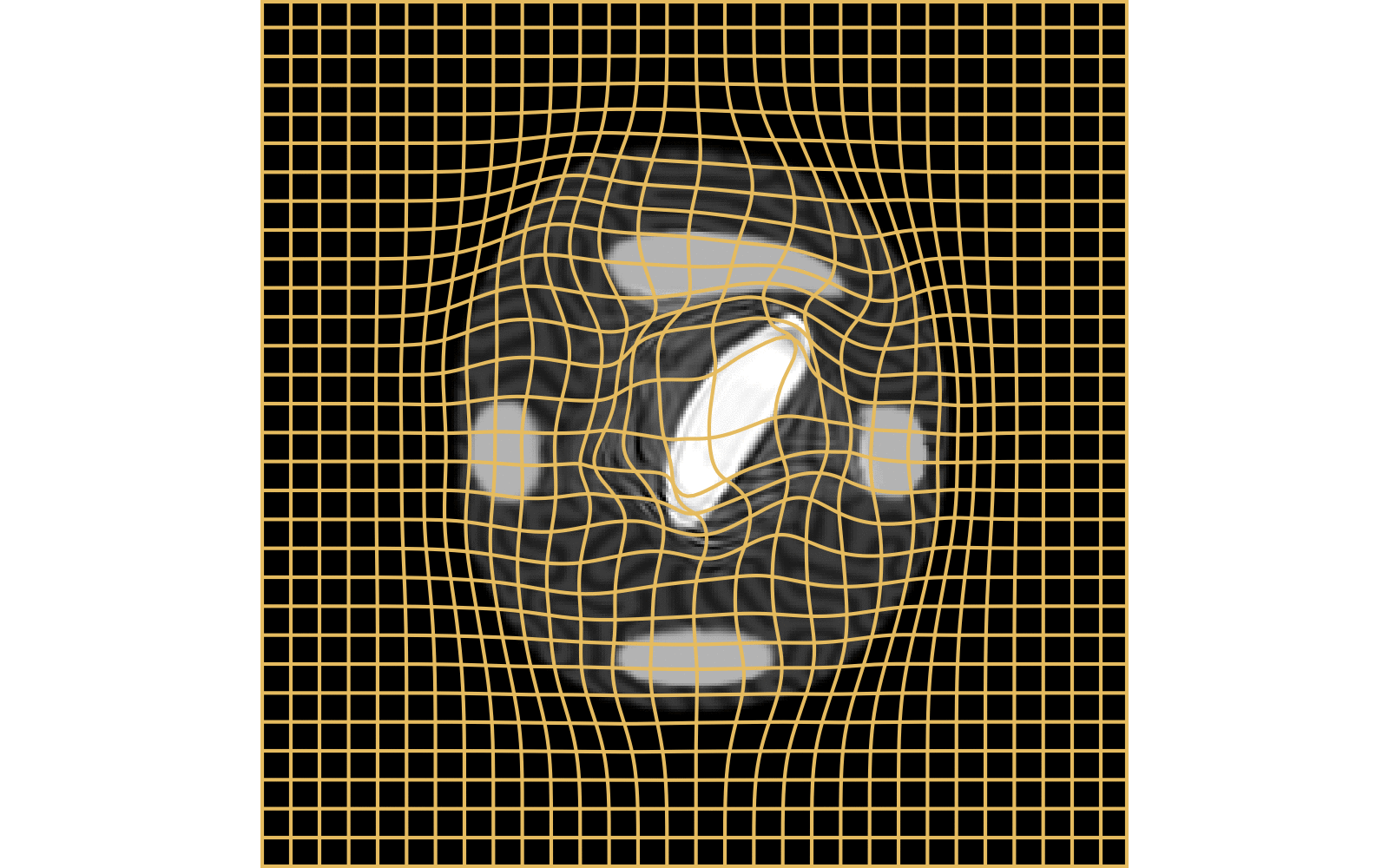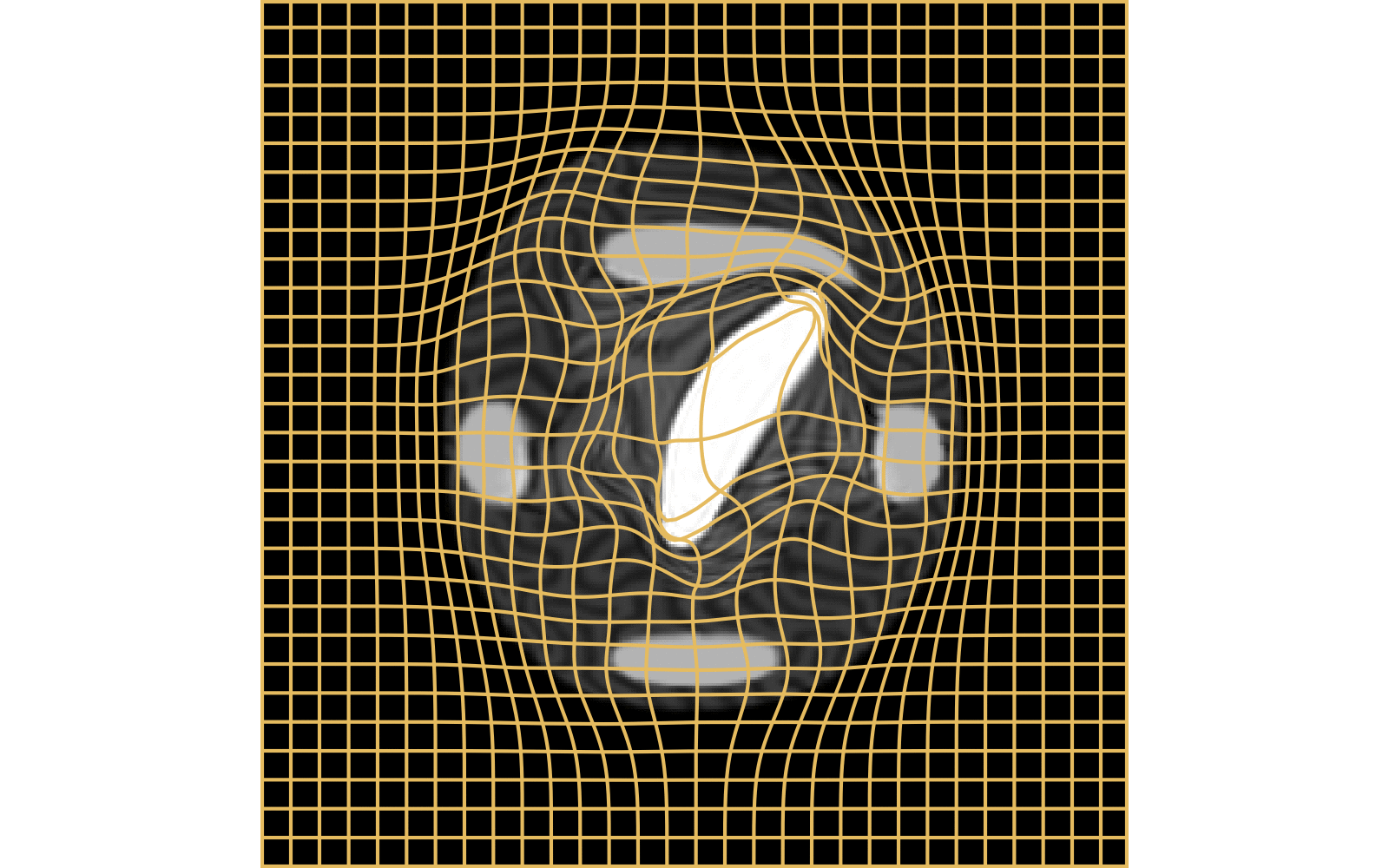

CM


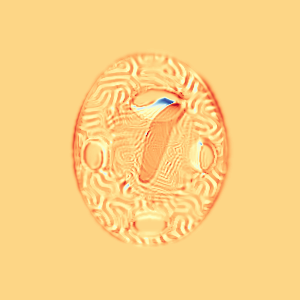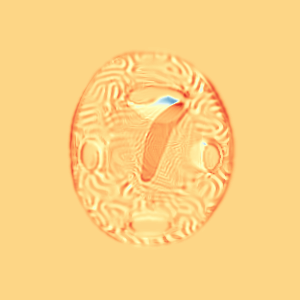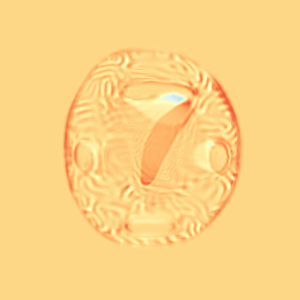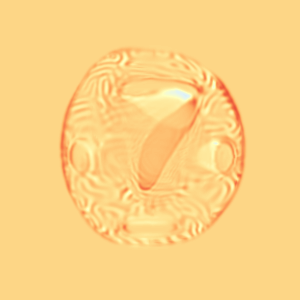
WM
\(I_t\)
\(I_t\) & \(\varphi^{v_t}\)
\(z_t\)
Constrained Metamorphosis
Results on ToyExamples













Anton François - 23/05/2023
On real data: BraTS 2021

- Big data-set
- 4 modalities
- Glioblastoma ground truth segmentation
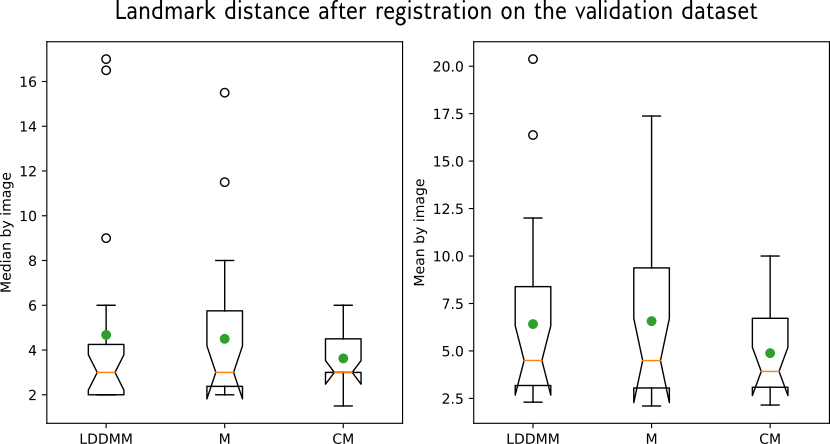
Registration validation using manually segmented ventricles (40 subjects).
Registered ventricles overlap measured with DICE score.
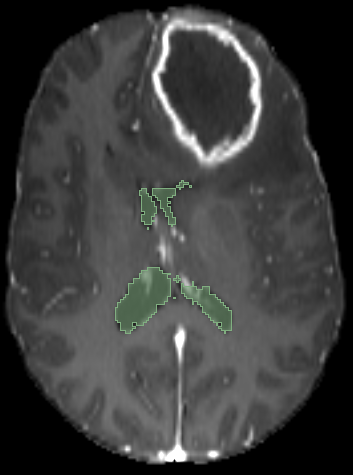
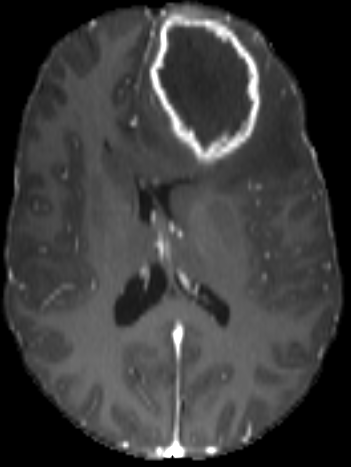
Constrained Metamorphosis
Weighted Metamorphosis
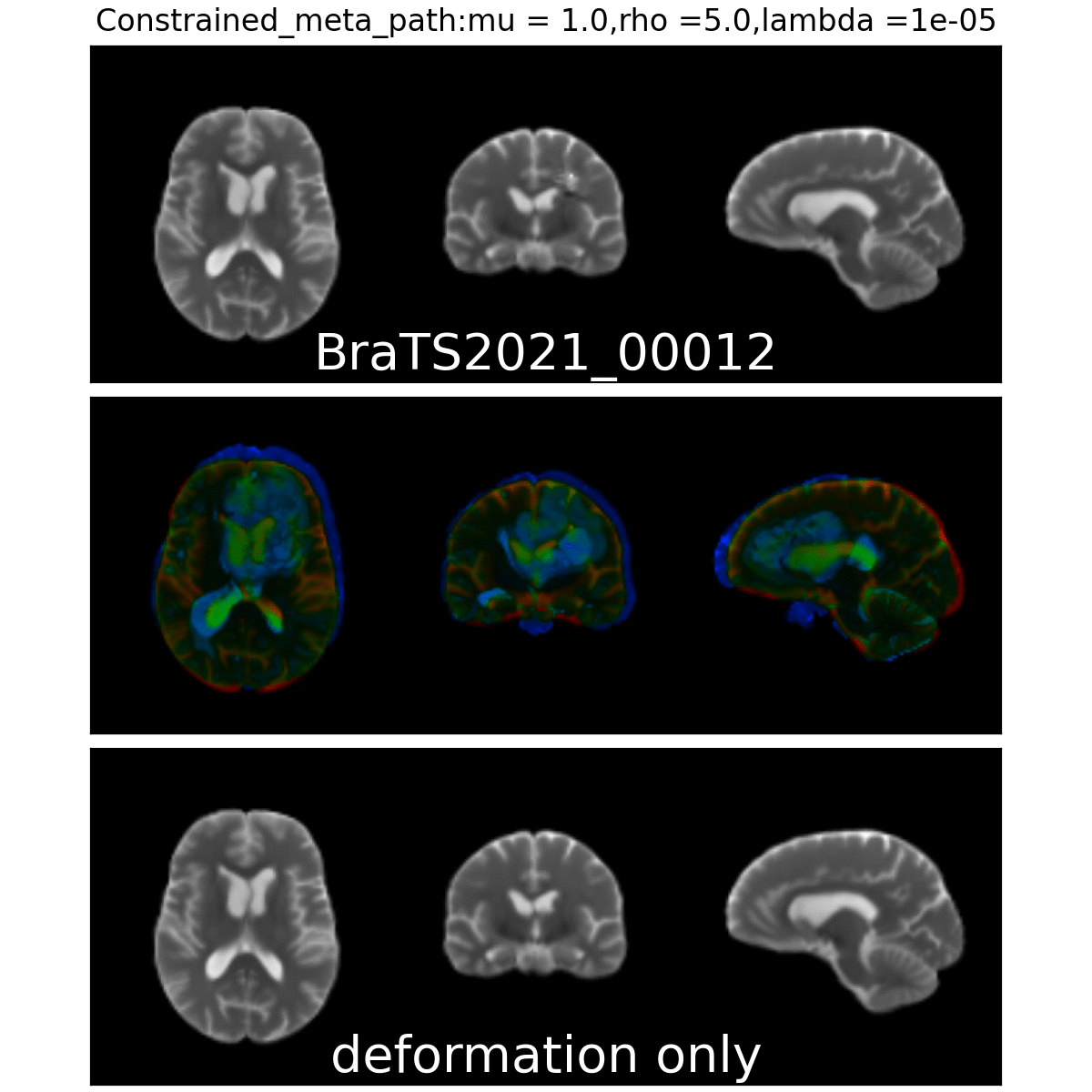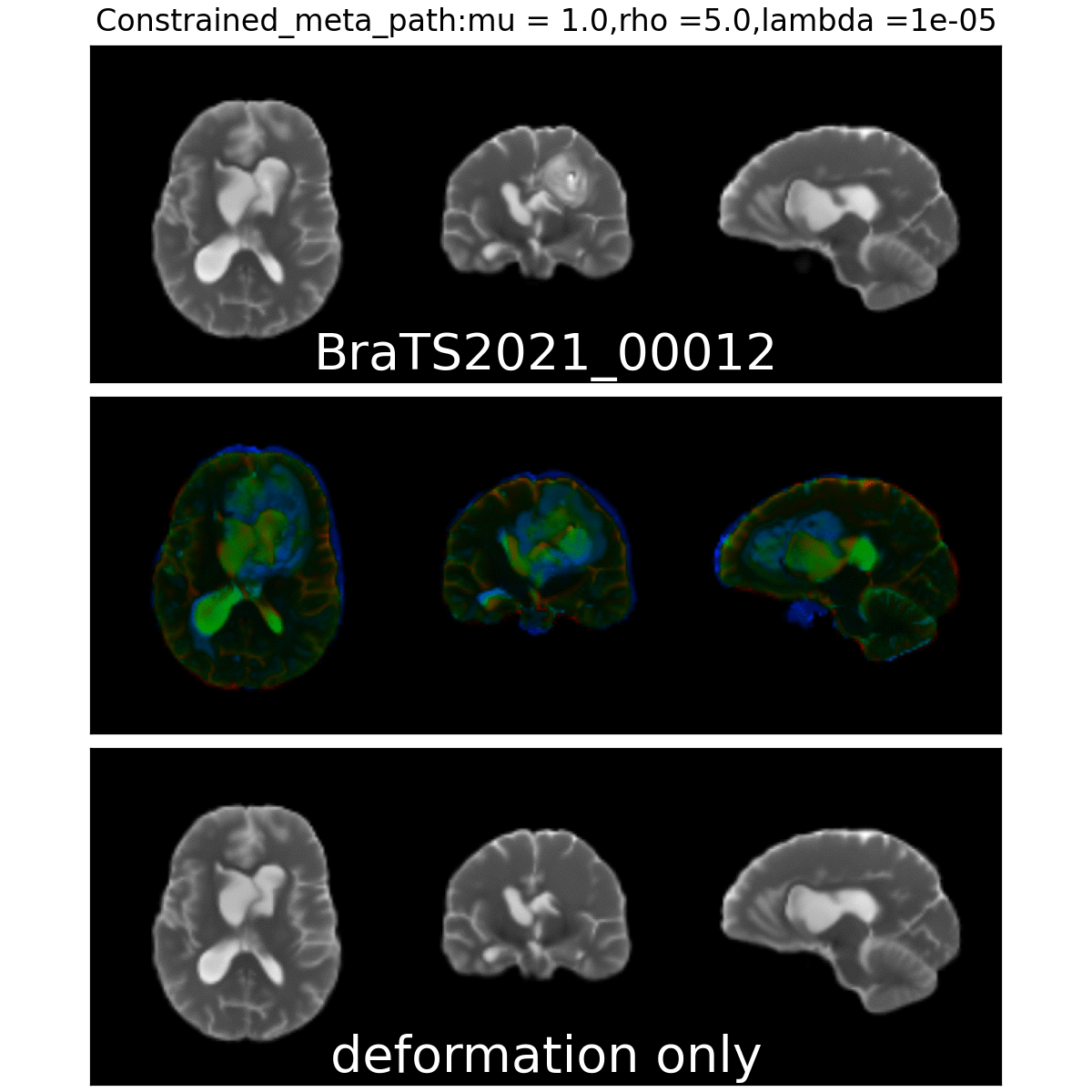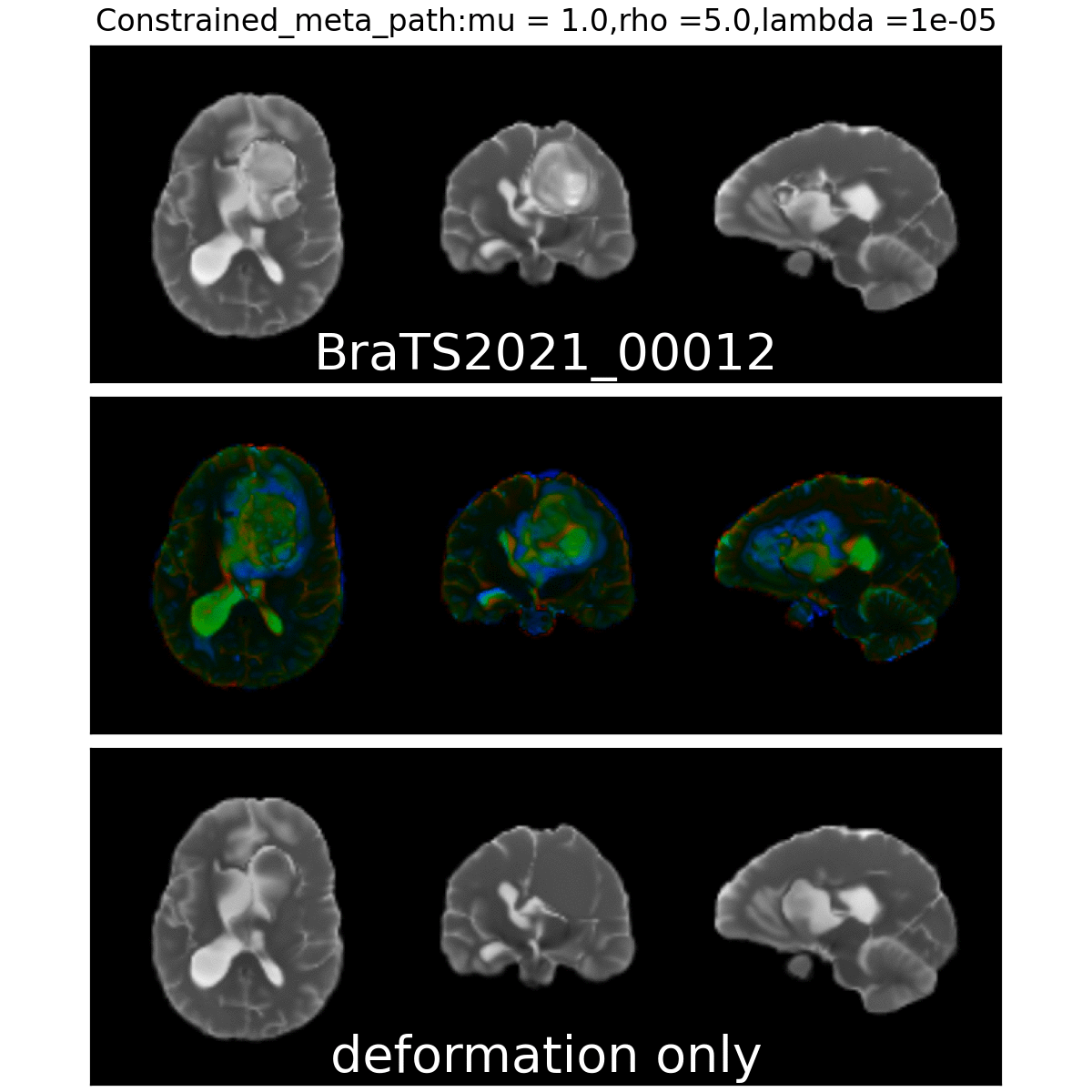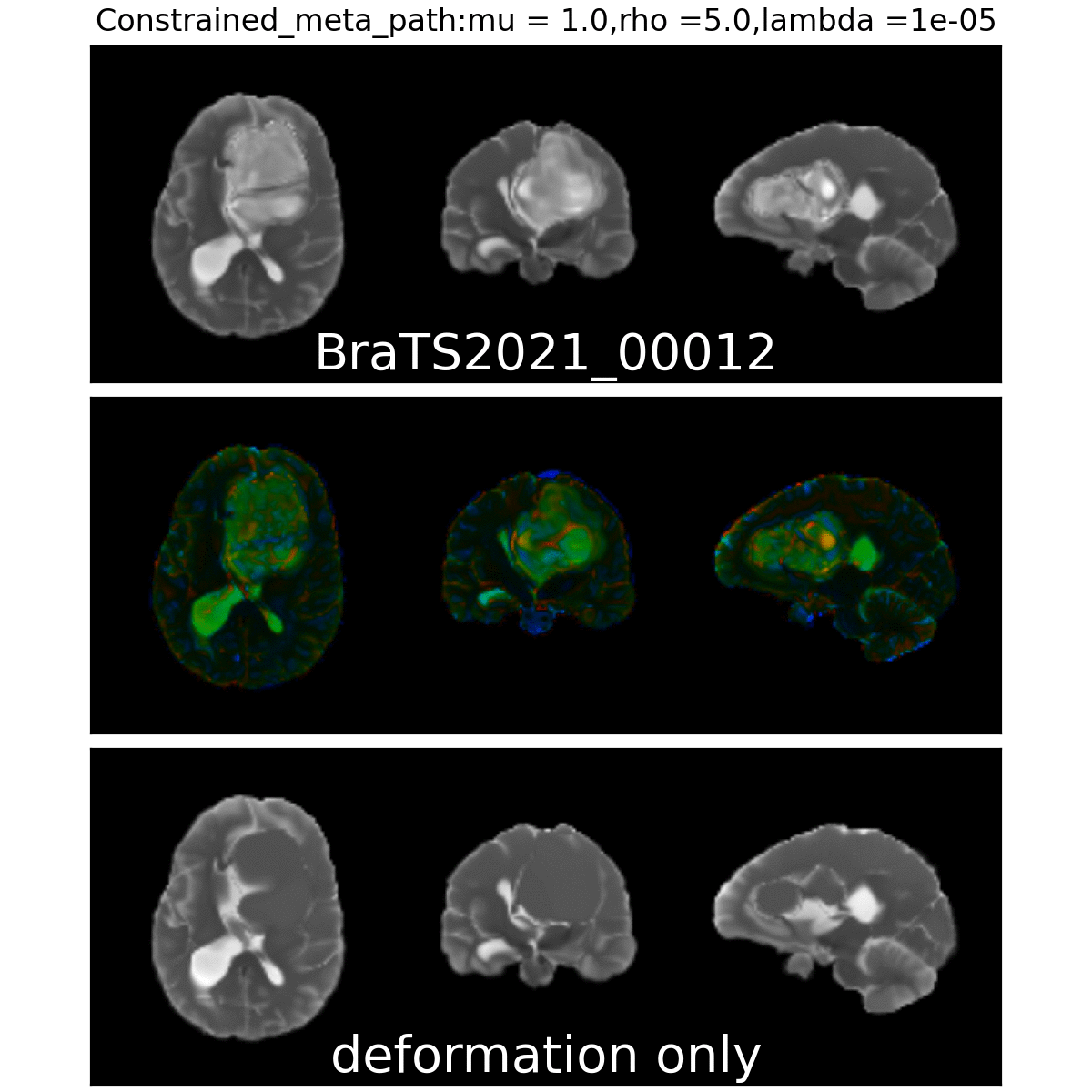
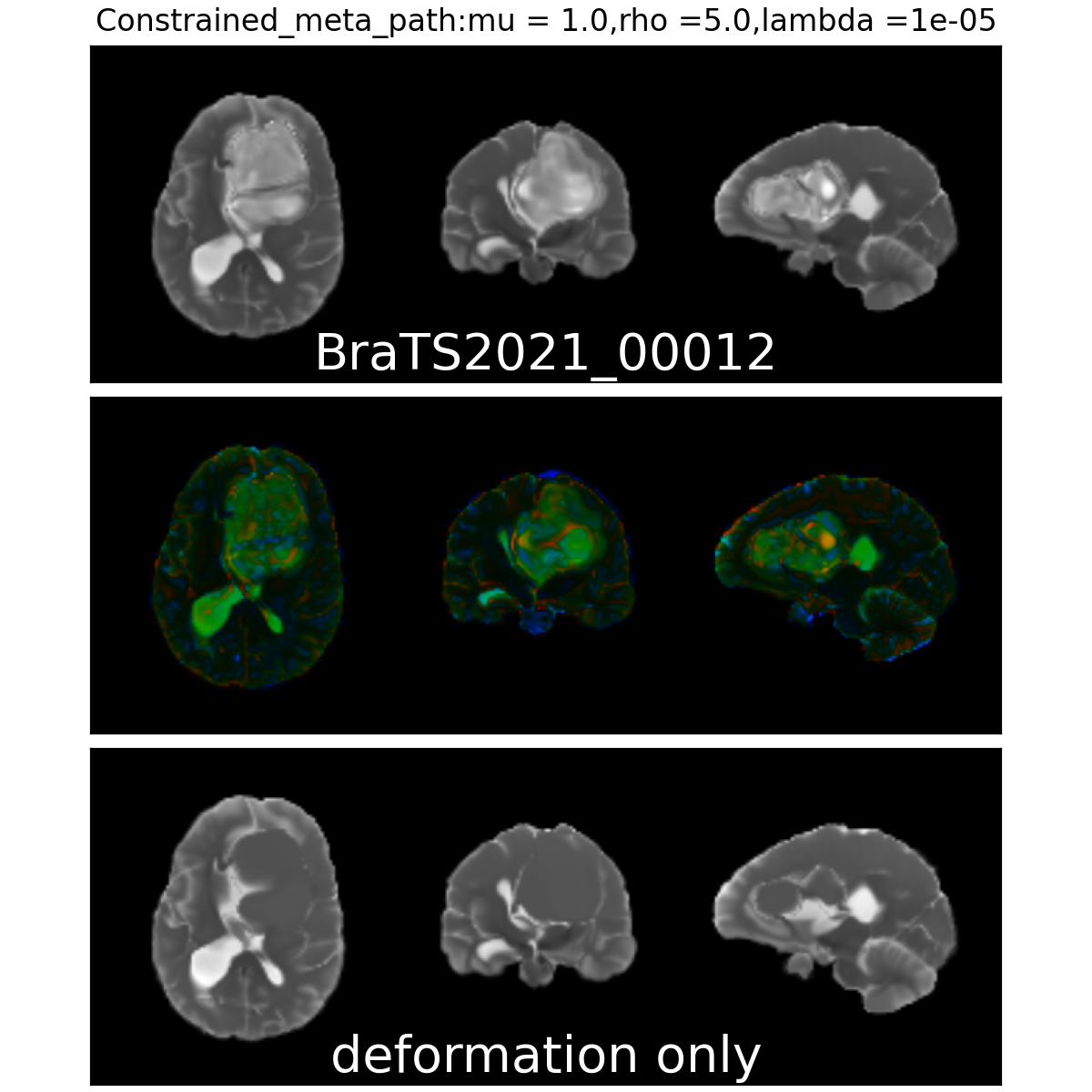
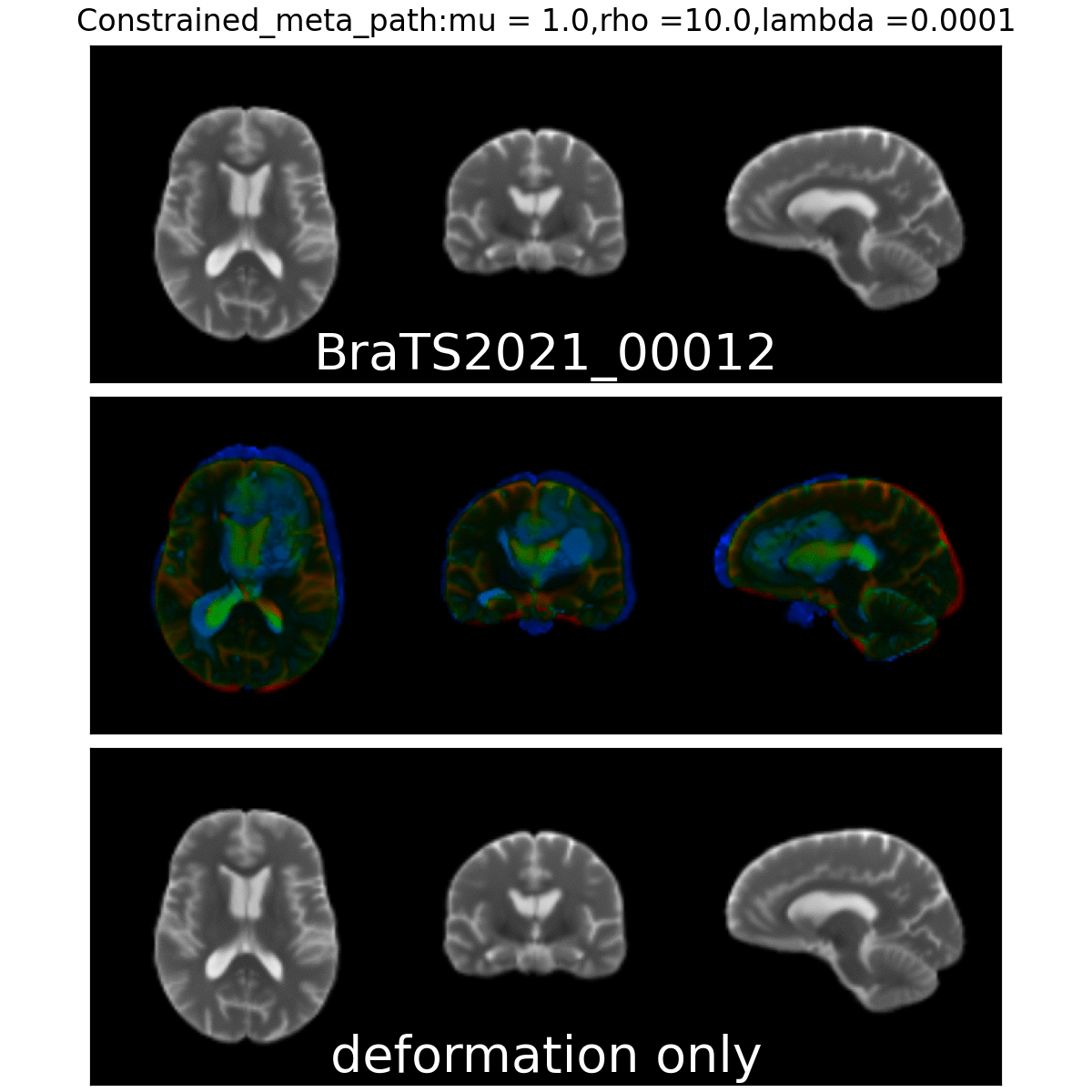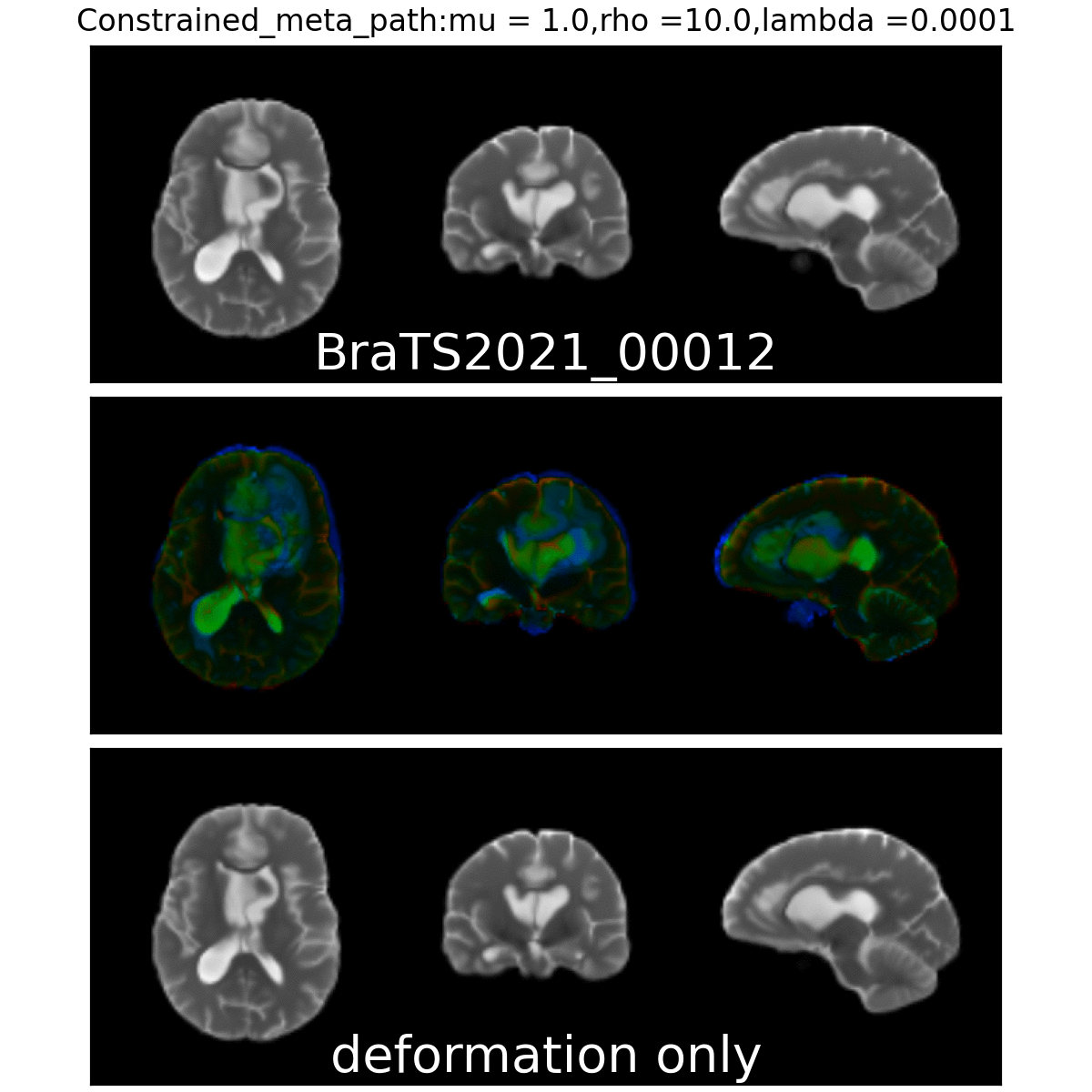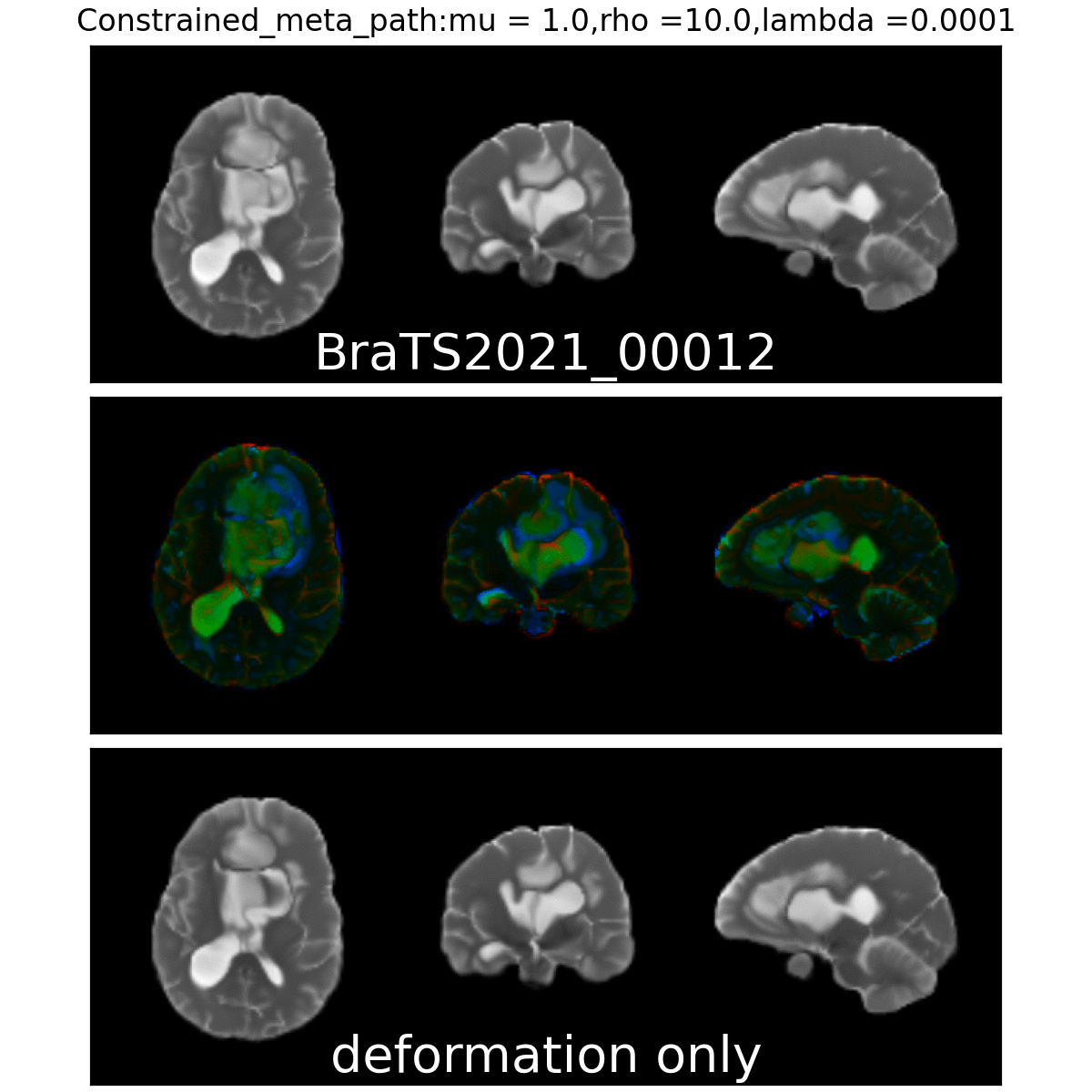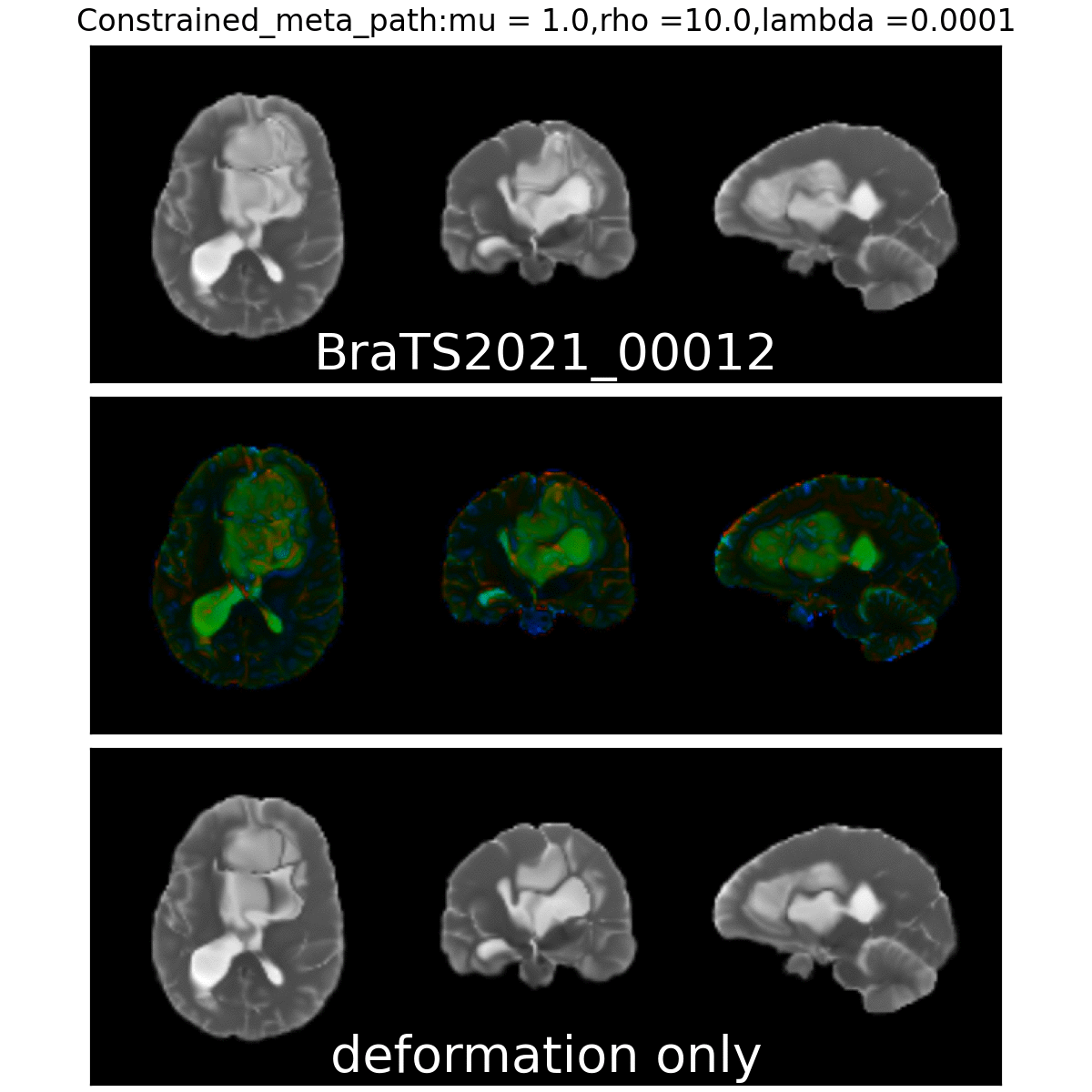













Anton François - 23/05/2023
Qualitative results
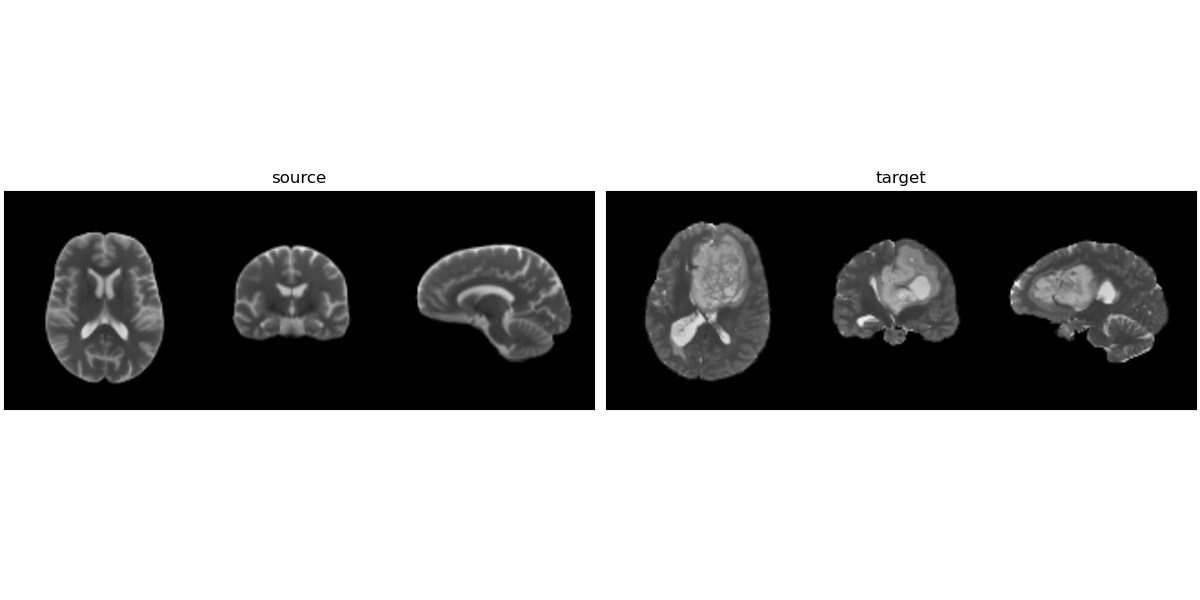













Anton François - 23/05/2023
Quantitative Results:
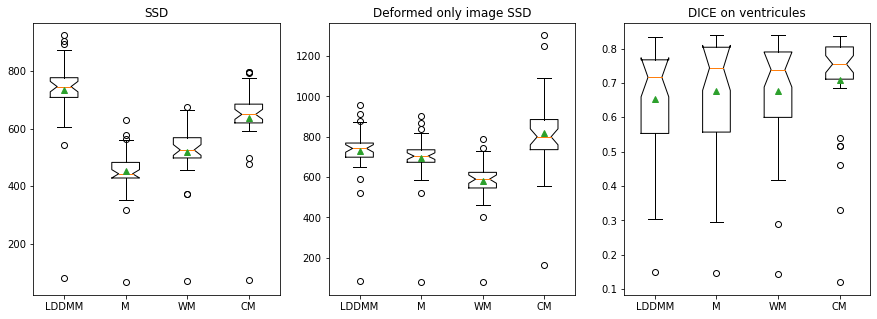
Lower the better
Higher the better













Anton François - 23/05/2023
BraTSReg pré- to post- operative registration
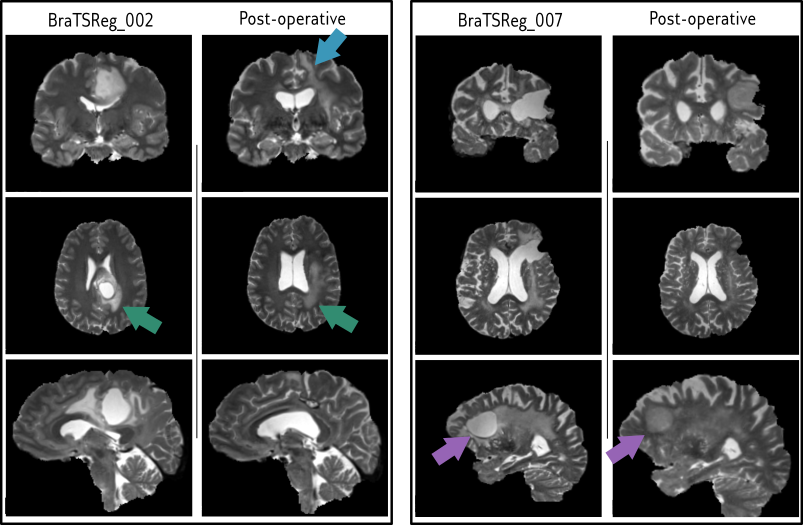
Lower the better
- Big datasets of the same patients before and after surgery
- Provides landmarks for registration validation













Anton François - 23/05/2023
Constrained Metamorphosis
conclusion & perspective
Framework to add priors into Metamorphosis

Slower because of the increasing complexity













Anton François - 23/05/2023
Constrained Metamorphosis
conclusion & perspective
Framework to add priors into Metamorphosis
We have shown that growth has to drive registration
Implement Deep-Learning Version.
Prior modelisation: We can incorporate more complex glioma model (e.g., GLISTR [Gooya et al.]) or a growth model [Kaltenmark, 2016].
Versatile: can be used for healthy/pathological or pathological/pathological applications or others.
Automatic prior selection
TDA Glioblastoma
Segmentation


Raphaël Tinarrage
TDA Glioblastoma Segmentation



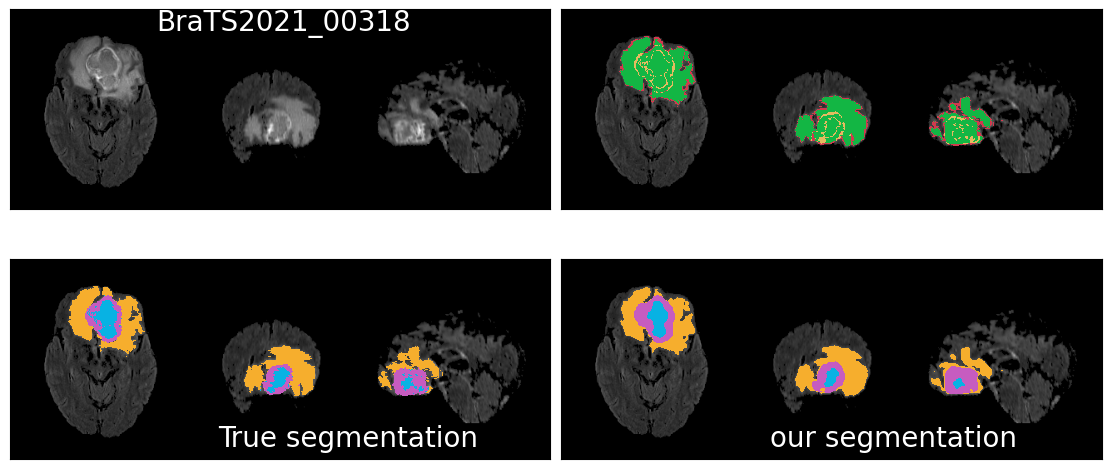




Conclusion & Perspective




Anton François - 23/05/2023
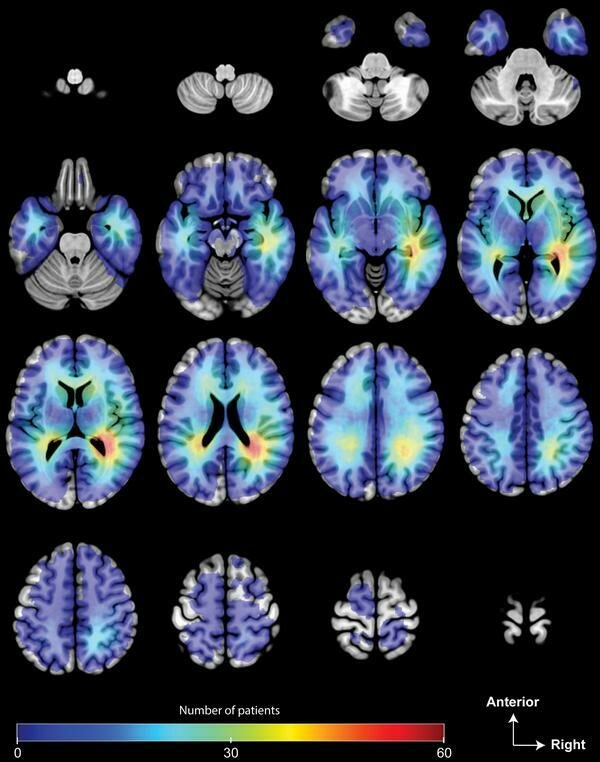
Statistical Atlas: [Roux, 2019] Glioma frequency of apparition by voxels.
Allows to show correlations between glioma location and symptoms




Anton François - 23/05/2023
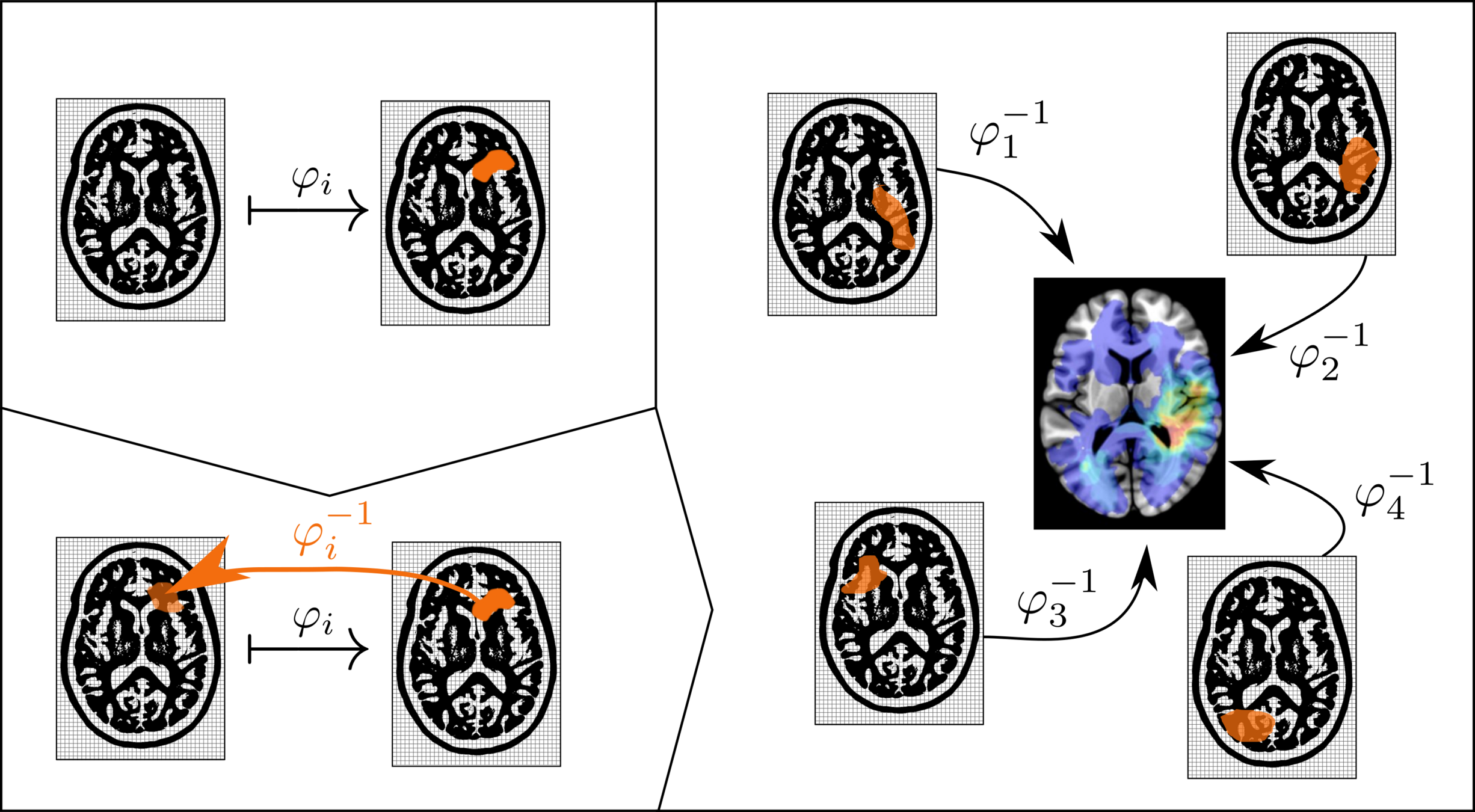
A Diffeomorphic Atlas represents shape variations, it is a Template along with registrations from the template to each data points (images)
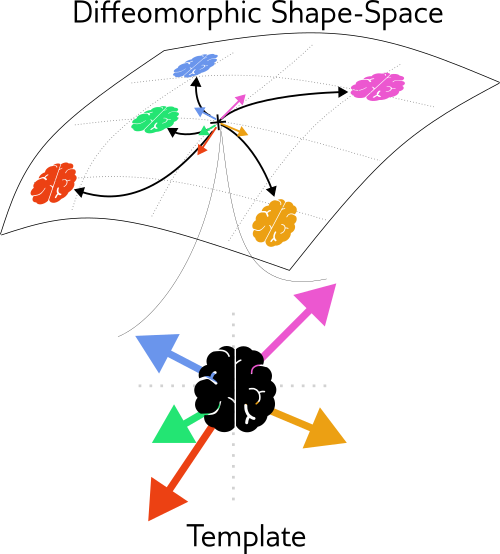
Given a sequence of images \(I^1,\dots,I^n\) and a notion of distance \(d\) corresponding to the length of a geodesic path in shape space. We compute the template \(T\) by minimising:
$$\mathcal M(T) = \frac{1}{2n} \sum_{k=1}^{n} d(T,I^k)^2$$








Speculations about atlases.
Can we build a Metamorphic atlas ?
How to estimate \(T\) for a glioma data base?
A combination of a Statistical Atlas and a diffeomorphic shape space.
Anton François - 23/05/2023
Can we build a CM atlas ?
Not as it is: Because it is prior dependent, one can not define a single metric for a whole data set
Technically speaking, yes but there are interpretability issues.




Overall outcomes & Perspectives
First open-source implementation of Metamorphosis, with novel integration scheme and GPU support.
Framework to register complex medical images with increased explainability using a simplitistic model.
Glioblastoma segmentation method using TDA
Published Articles:
- A. François, P. Gori, and J. Glaunès. Metamorphic image registration using a semi-lagrangian scheme. In SEE GSI, 2021
- A. François, M. Maillard, C. Oppenheim, J. Pallud, I. Bloch, P. Gori, and J. Glaunès. Weighted metamorphosis for registration of images with different topologies. In WBIR, pages 8–17, 2022
- M. Maillard, A. François, J. Glaunès, I. Bloch, and P. Gori. A deep residual learning
implementation of metamorphosis. In IEEE ISBI, 2022




Th
an
k
You !