Some AMM Theory
Basic Requirements
- Two assets:
- cash and an asset
- deposits in pool of \(c\) cash and \(a\) asset
- AMMs should be self-contained: pricing rule based on liquidity only on \(a,c\)
- implied price of the asset: \[p=\frac{c}{a}.\]
- marginal price: an infinitesimal unit should cost \[p^m=p\]
- trades involve changes of the asset in return for change in cash and transform \(a,c\)
- consider linear changes:
- a trade of \(q\in(-\infty,a),\) costs \(\Delta c(q)\)
- liquidity changes to \(a-q,c+\Delta c(q)\)
- \(\to\) marginal price after trade of \(q\) is \[p^m(q)=\frac{c+\Delta c(q)}{a-q}.\]
Some Pricing Rules from Traditional Markets: Uniform Price
- assume cost is price \(\times\) quantity: \[\Delta c(q)=q\cdot p(q)\]
- plus assume average price \(=\) marginal price
\[p(q)=\frac{c+q\cdot p(q)}{a-q}~~\Leftrightarrow~~p(q)=\frac{c}{a-2q}.\]
- formalized and analyzed by Canidio and Fritsch (2023) and implemented in COW-Swap
- Concern: a trader can split orders into infinitesimal quantities and earn a higher payoff.
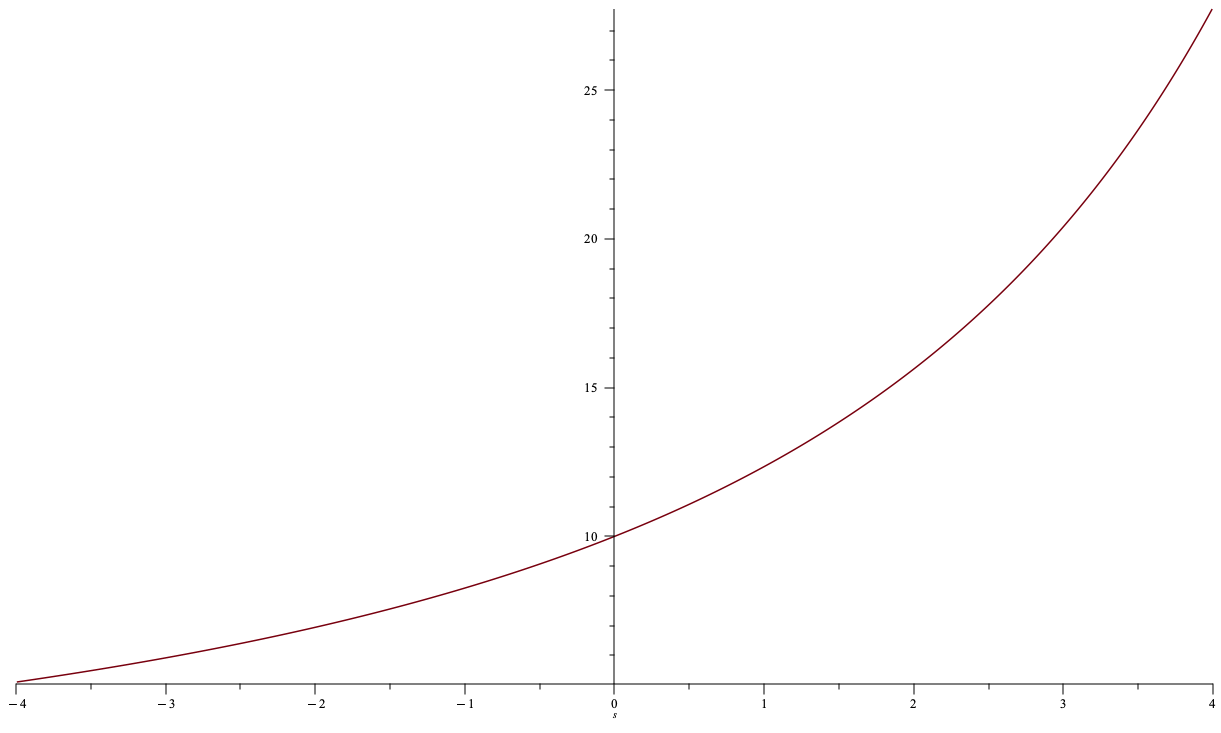
\(q=2\)
\(\Delta c(q)= q\times p^m(q)=2\times 15.5\)
Some Pricing Rules from Traditional Markets: Limit Order Book
- Liquidity providers submit sell orders \(s_1(p_1,q_1),\ldots,s(p_n,q_n)\)
- Matching engine sorts order increasing by price
-
someone who wants to buy quantity
\[q\in\left(\sum_{i=1}^{m-1} q_i,\sum_{i=1}^{m} q_i\right]~~~\text{pays}~~\Delta c(q)=\sum_{i=1}^mq_i\cdot p_i.\]
- For a simpler exposition, assume that the price-quantity curve can be expressed by a continuous marginal price function \(\rho(s)\) so that
\[\Delta c(q)=\int_0^q\rho(s) ds.\]
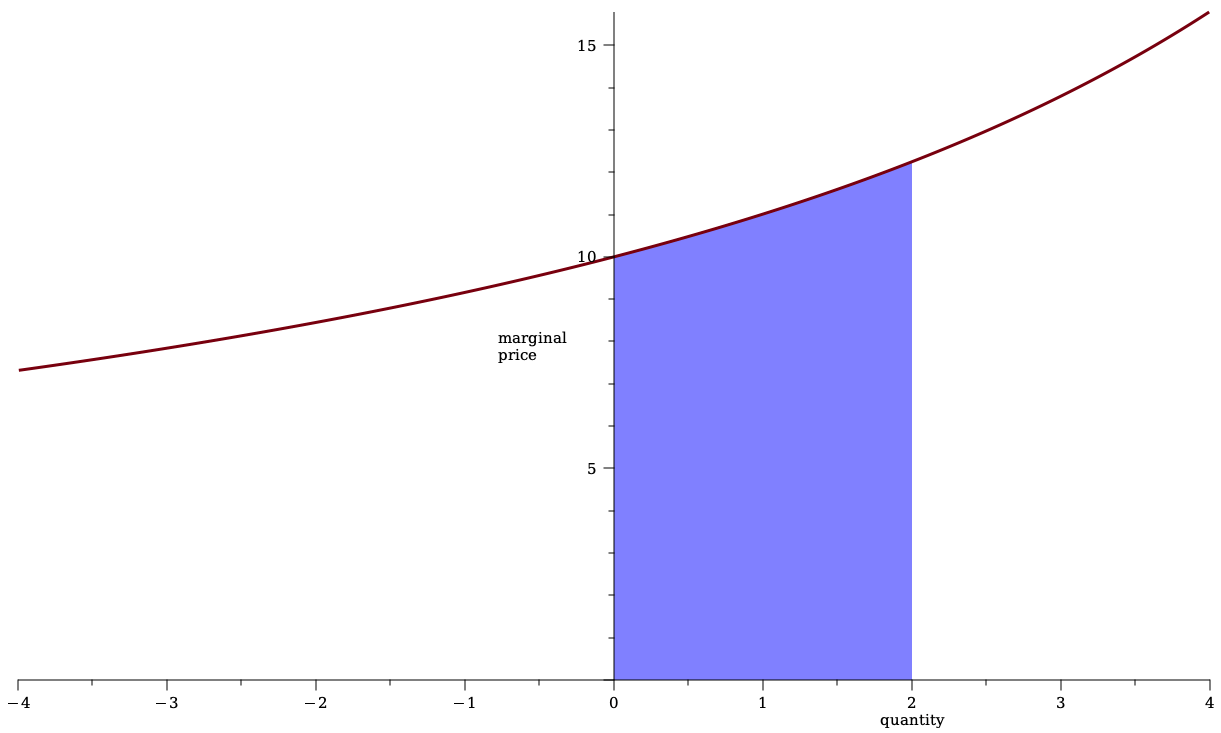
Some Pricing Rules from Traditional Markets: Limit Order Book
- For AMM: assume continuity \(\to\) price of "final" marginal unit coincides with price of "first" marginal unit of next trade \[\Delta c(q)=\int_0^q \rho(s) ds~\to~\Delta c'(q)=\rho(q)=p(q),~~ \Delta c(0)=0.\]
- Also "first" unit costs nothing \(\Delta c(q)=0\)
- This brings differential equation
- \[p(q)=\frac{c+\int_0^q \rho(s) ds}{a-q}~~\Leftrightarrow~~\Delta c'(q)=\frac{c+\Delta c(q)}{a-q},\]
with solution \[\Delta c(q)=q\cdot\frac{c}{a-q}.\] - Or, we can write \[\Delta c(q)=\int\limits_0^q p(s)ds=\int\limits_0^q\frac{ac}{(a-q)^2}ds=\frac{cq}{a-q}.\]
note: if you do uniform pricing and split your order into infinitesimal units, then you pay the limit order price
Most Common Pricing Rule in DeFi: Constant Product
- For AMM: assume "constant" liquidity
- Liquidity defined as product of deposits
-
\(\to\) liquidity before and after trade coincides
\[a\cdot c= (a-q) (c+\Delta c(q))\] -
This implies cost
\[\Delta c(q)=q \frac{c}{a-q},\] average price \[p(q)=\frac{c}{a-q}\]
and marginal price \[p^m(q)=\frac{c+\frac{cq}{a-q}}{a-q}=\frac{ac}{(a-q)^2}.\]
Insight: AMM pricing function is the same as a limit order book when we require
- that prices are continuous and
- that prices are determined by liquidity deposits only