Market Design with Blockchain Technology

Katya Malinova and Andreas Park

Why is Blockchain Important? What can it do?

 

  • World Wide Web:

    • frictionless electronic transfer of information

  • Blockchain:

    • ​frictionless electronic transfer of value

Illustration: Money Transfer

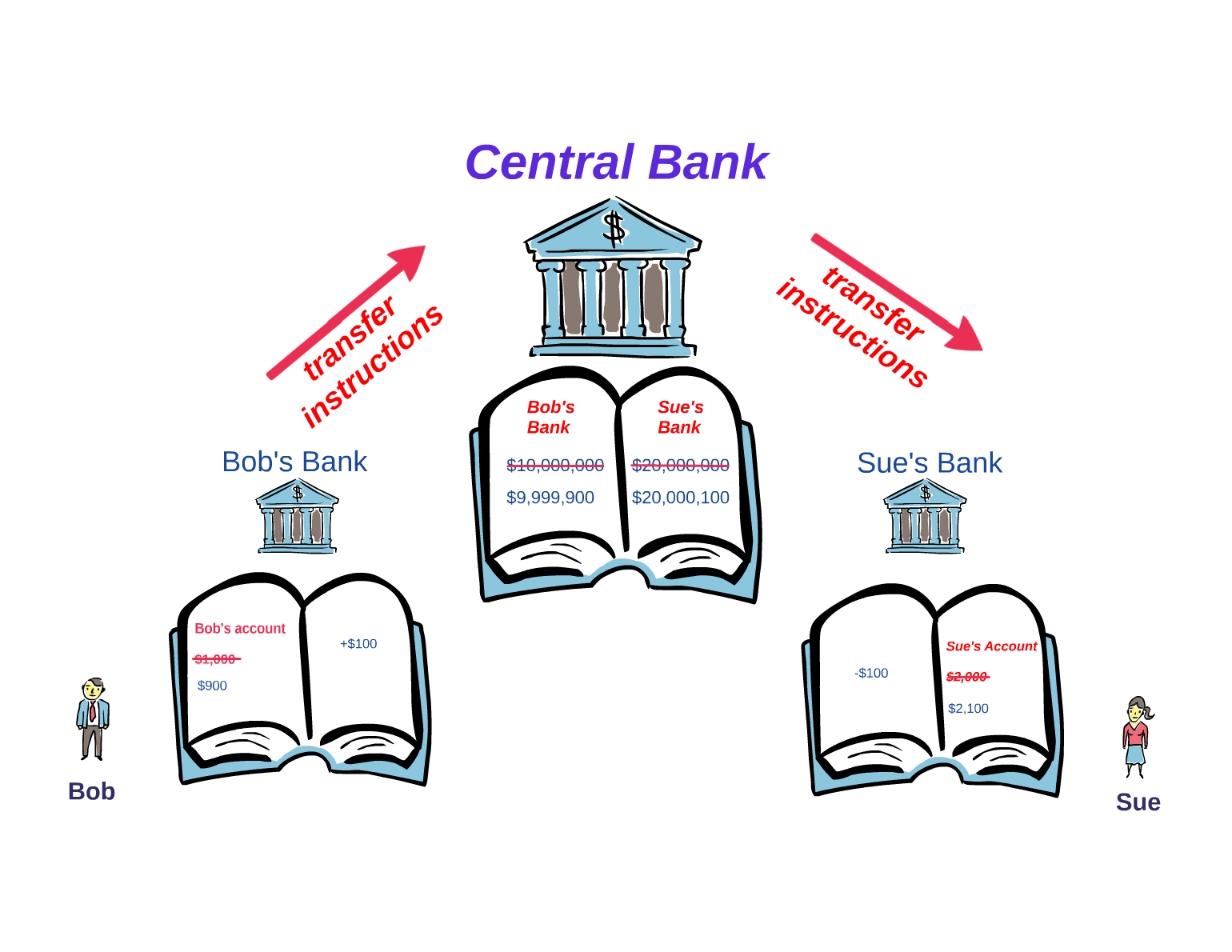
Illustration: Stock Trade

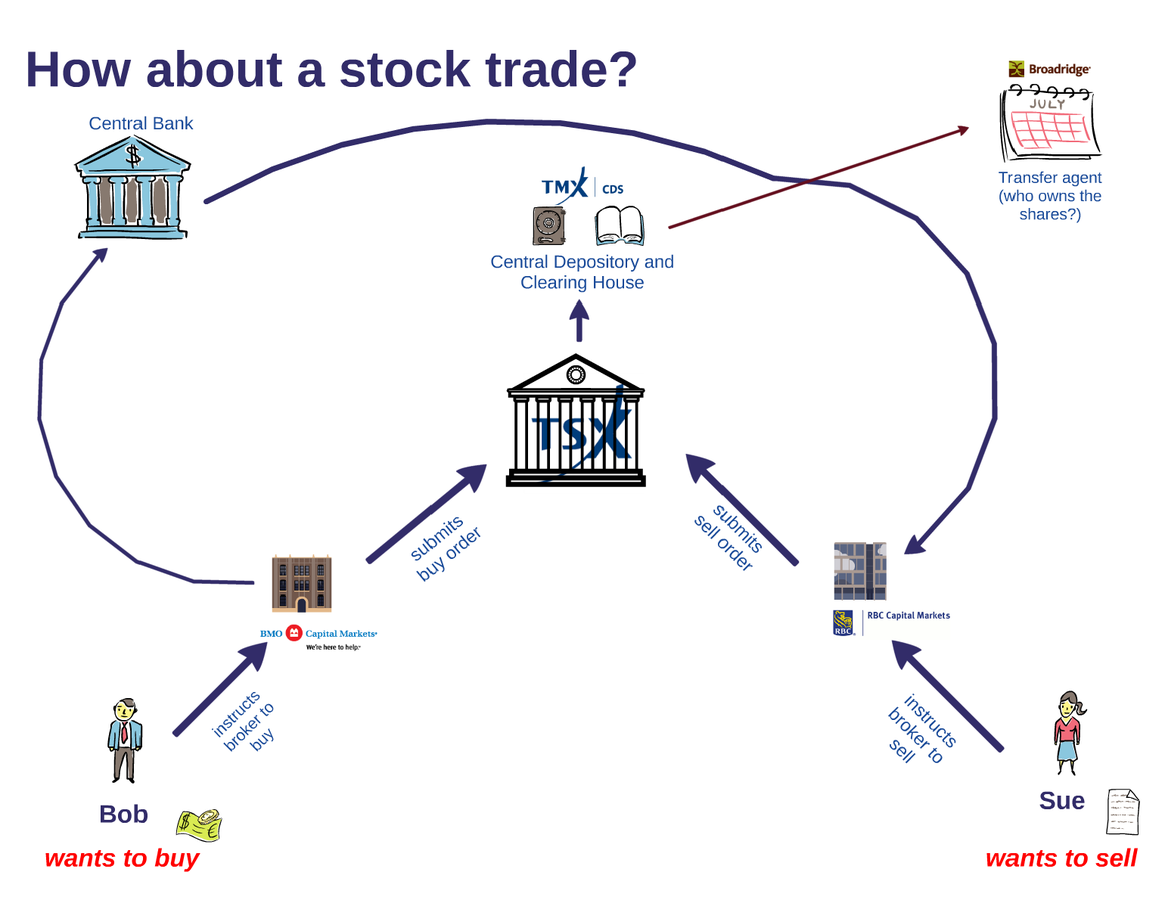
Illustration: Money Transfer

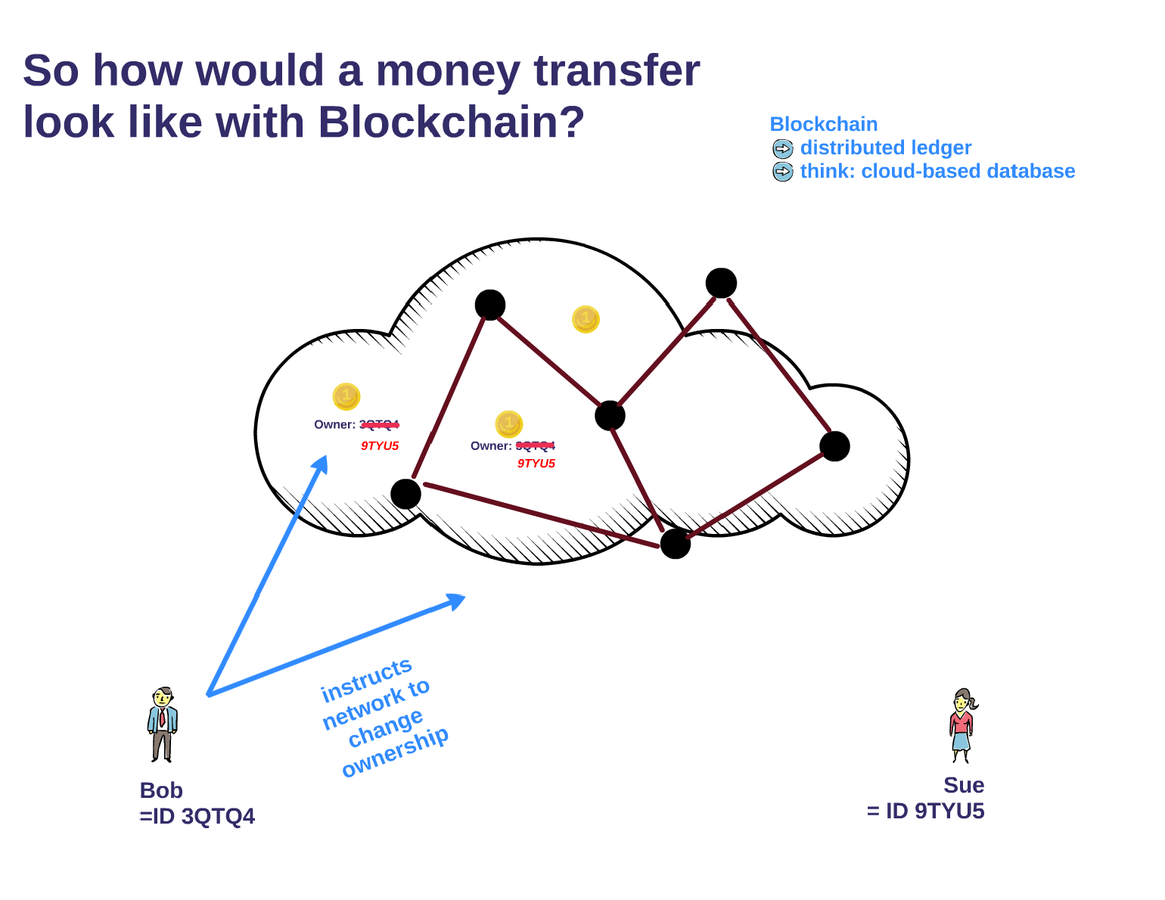
Illustration: Stock Trade

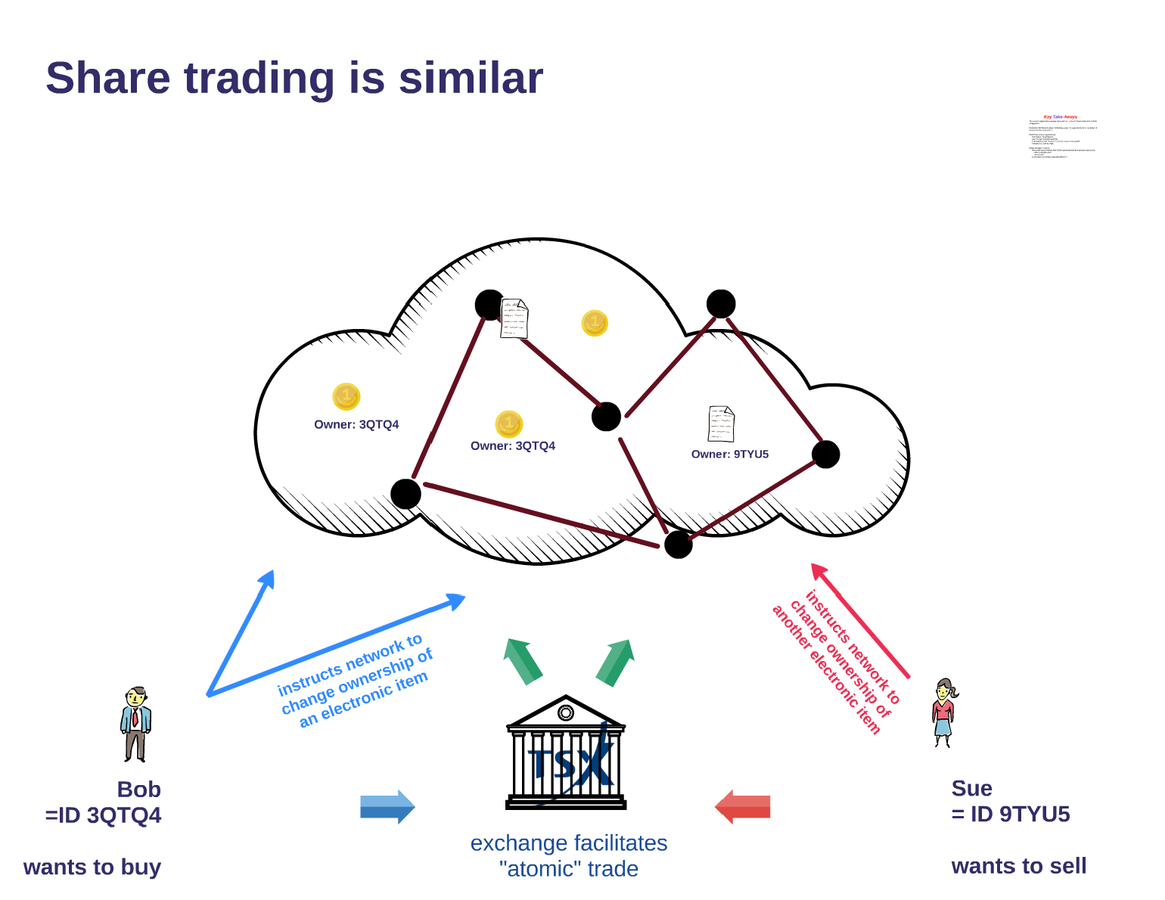
A version with an exchange

Illustration: Stock Trade

A version without an exchange but with smart contracts

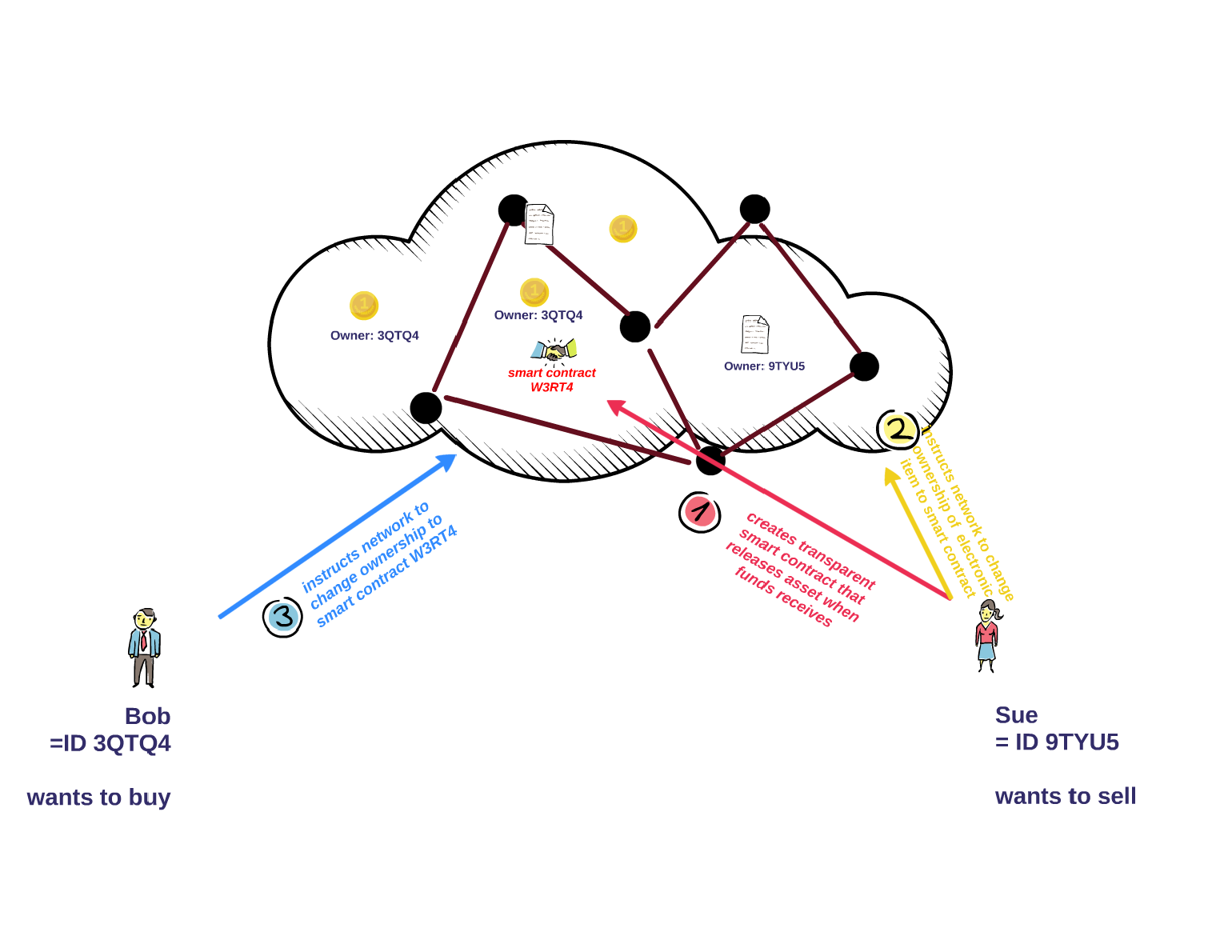
Take Aways: Intrinsic Features of Blockchain

  • Blockchain requires no "accounts", dealers/brokers, only the network is needed
  • Peer-to-peer is possible.
  • Blockchain ledger can be very transparent
    • => design choice.
  • Who is your peer ... ?

For this paper

Also interesting

  • Settlement is immediate
    • implications for intermediaries
    • => paper by Zoican & Khapko (2017)
  • How do you pay for validation?
    • Service by network organizers?
    • Incentives as in Ethereum or Bitcoin?

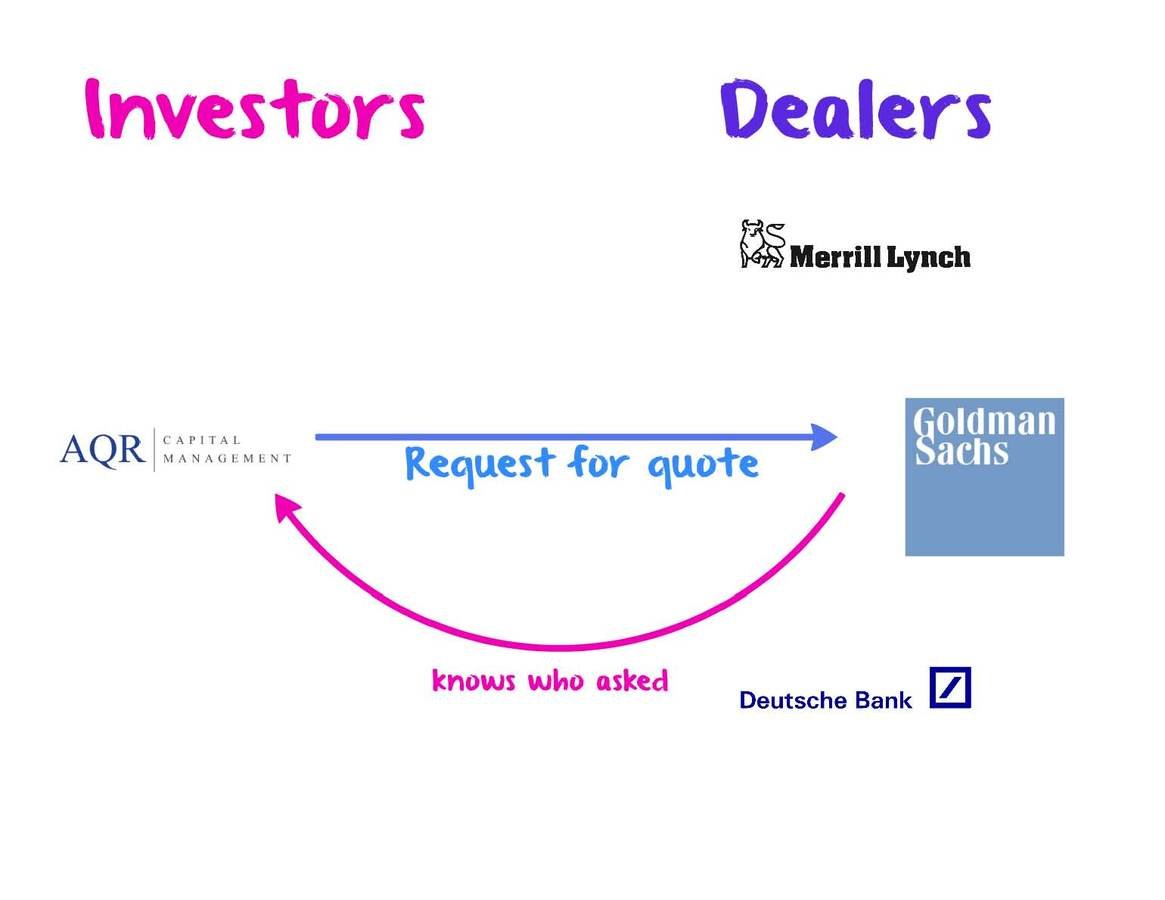
What do you know and what do you not know in OTC?

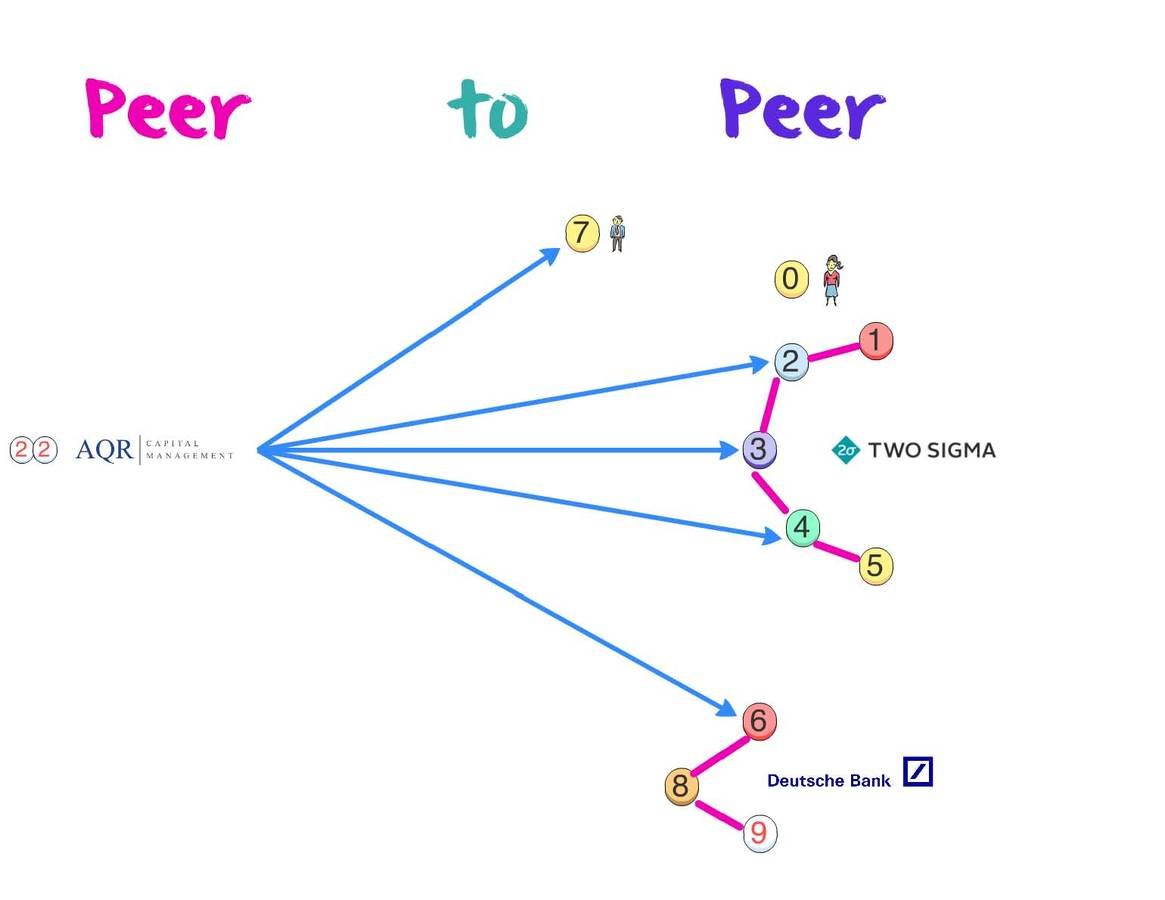
What do you know and what do you not know in Peer-to-Peer?

Key Research Question

How does the design of ledger transparency and identifier-usage with possible P2P interactions affect trading behavior and economic outcomes?

  • different ledger transparency regimes are possible
    • ledger is open to all
    • ledger is hidden
  • different identifier-usage regimes are possible
    • use single IDs per entity
    • use arbitrary number of IDs

Who benefits and loses under which regime?

Our Paper: Two Markets

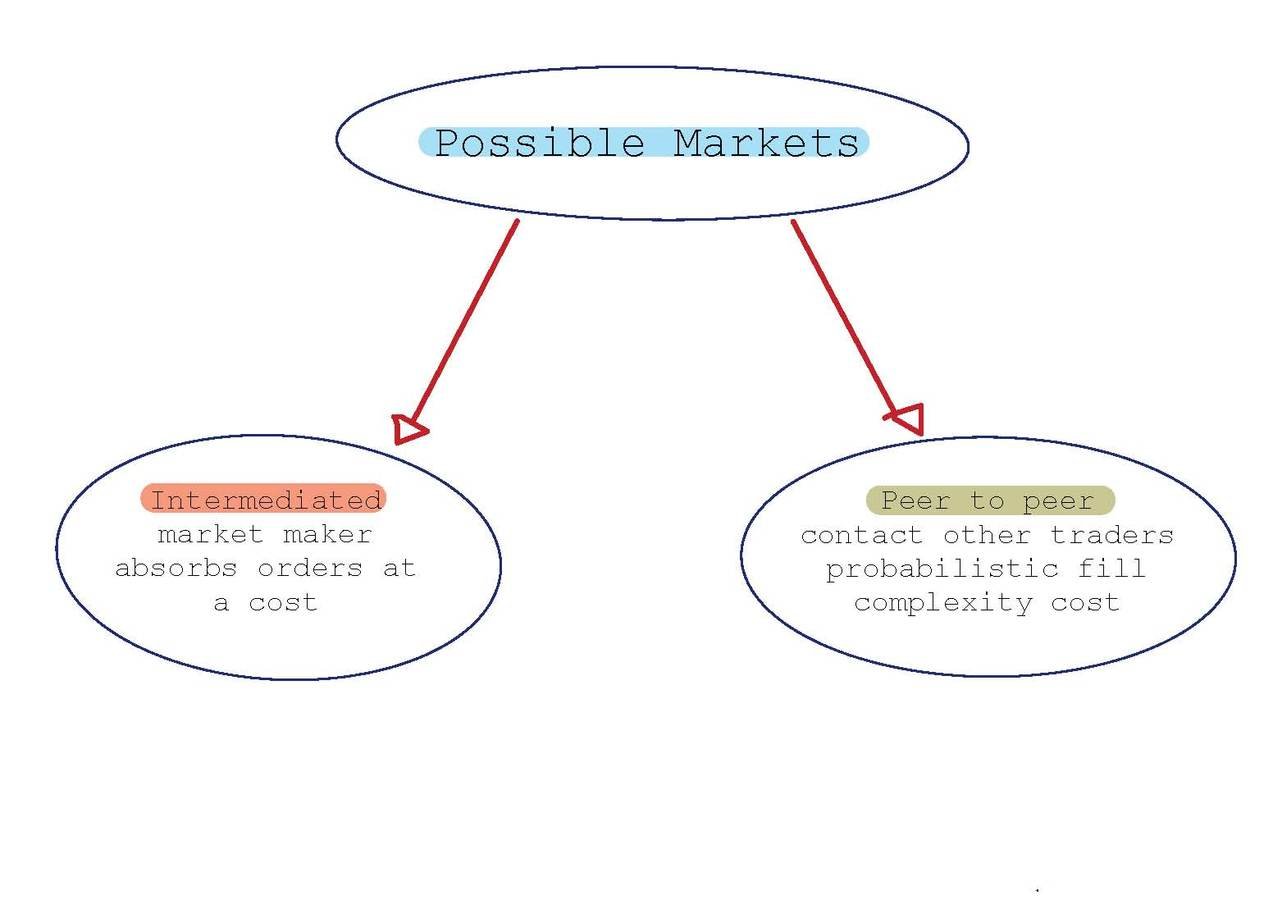
Three design choices:

  1. anonymous peer to peer, 1 ID per investor

  2. non-anonymous peer to peer, 1 ID per investor

  3. anonymous peer to peer, multiple IDs per investor

Model Ingredients

  • Risky asset, normally distributed 
  • Two large investors

    • Each period one is hit with size Q=1 liquidity shock.

    • Other can absorb the shock at zero cost.

  • ​Continuum of 1/  small investors
    • ​trade with probability                 at "public" price
    • each period, mass 1 wants to buy, mass 1 wants to sell
    • Data processing/complexity to contact mass q
    • Contact mass q:
      • pay        and trade quantity   
      • cost c is a loss to aggregate welfare
N(0,\sigma^2)
N(0,σ2)N(0,\sigma^2)
\rho\le1/2
ρ≤1/2\rho\le1/2
\rho q
ρq\rho q
\frac{c}{2} q^2
c2q2\frac{c}{2} q^2
\rho
ρ\rho

Model Ingredients (II)

 

  • Risk-averse intermediaries, maximize CARA utility
    • Assumption: start each period with 0 inventory
  • Linear mining/validation cost:
    • pay       to trade with     counterparties
\gamma q
γq\gamma q
q
qq

Disclaimer:

  • no asymmetric information here
  • => not applicable to all asset classes
  • But: equities are probably not the first choice for blockchain-based trading
    • instead: bonds, derivatives, swaps

Economic Mechanisms

  • Total desired amount trades by non-intermediaries
    • ​buy = 2
    • sell = 1
    • latent liquidity to offset the buy = 1
  • net-demand: mass 1
  • if small seller trade with large buyer, then
    • small buyers must trade with the intermediary
      • => welfare loss
    • large incurs search cost
      • => welfare loss
  • large buyer can trade with large seller without price impact
    • no price change
    • all other cases: price effect & welfare loss

Role of the Intermediated Market

  • Risk averse intermediaries offer demand schedule 
  • Maximize expected utility =>
    • CARA-Gausiaan setup 
    • => CAPM utility 
    • maximize certainty equivalent of future wealth

based on Biais (1993)

\max_{q_i}[I_i\times V-(V-p)q_i] -\frac{\kappa}{2}\sigma^2[-q_i+I_i]^2,
maxqi[Ii×V−(V−p)qi]−κ2σ2[−qi+Ii]2, \max_{q_i}[I_i\times V-(V-p)q_i] -\frac{\kappa}{2}\sigma^2[-q_i+I_i]^2,
  • Yields FOC
V-p-\kappa \sigma^2 \times I_i +\kappa \sigma^2q_i=0.
V−p−κσ2×Ii+κσ2qi=0.V-p-\kappa \sigma^2 \times I_i +\kappa \sigma^2q_i=0.
  • an then demand schedule
q_i(p) = -\frac{V-p}{\kappa\sigma^2} +I_i.
qi(p)=−V−pκσ2+Ii.q_i(p) = -\frac{V-p}{\kappa\sigma^2} +I_i.

Role of the Intermediated Market

  • applying market clearing we get the price

based on Biais (1993)

p^\mathsf{mm}(I,q)= V+ \frac{\kappa \sigma^2}{N}\ (-I+q)
pmm(I,q)=V+κσ2N (−I+q) p^\mathsf{mm}(I,q)= V+ \frac{\kappa \sigma^2}{N}\ (-I+q)
\ell:=\frac{2\kappa \sigma^2}{N}
ℓ:=2κσ2N\ell:=\frac{2\kappa \sigma^2}{N}

define as liquidity measure

  • to get payoff function for trading q with intermediaries that hold inventory I:
\pi^\mathsf{mm} (I,q)=q\times(V-p^\mathsf{mm}(I,q))=-\frac{\ell}{2}\ q(q-I)
πmm(I,q)=q×(V−pmm(I,q))=−ℓ2 q(q−I)\pi^\mathsf{mm} (I,q)=q\times(V-p^\mathsf{mm}(I,q))=-\frac{\ell}{2}\ q(q-I)

Role of the Intermediated Market

  • Some insights:
    • Inventory I "shifts" public price by​
    • Model feature:​
      • net-trades with intermediary = inefficient transfer of risk
      • => welfare reducing.
\ell/2\times(-I)
ℓ/2×(−I)\ell/2\times(-I)

 Peer to Peer Setting I:
Non-transparent & concentrated ownership

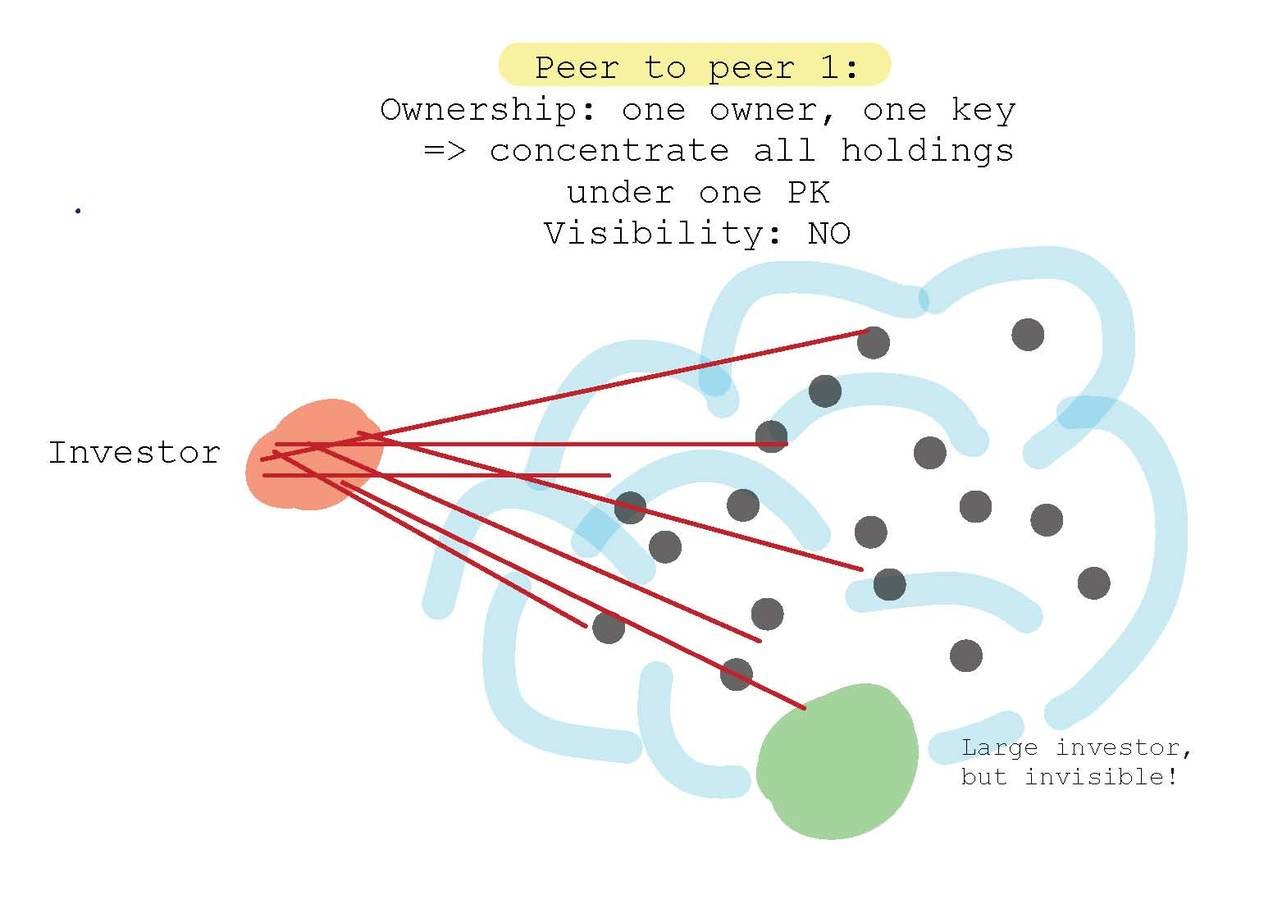
Note: Nothing in this setup requires Blockchain Tech — ITG’s POSIT Alert, Algomi, or "all-to-all" platforms already facilitate anonymous peer-to-peer.

Relative to all trading with intermediaries

  • Contact mass x of investors such that 

data cost

current market price paid to small

costly trading with intermediary

validation cost

\max_x -\frac{c}{2}x^2-\rho \gamma x-x\rho\frac{\ell}{2}\times (-I) - (1-\rho x)(1-\rho x -I)\times\frac{\ell}{2}.
maxx−c2x2−ργx−xρℓ2×(−I)−(1−ρx)(1−ρx−I)×ℓ2.\max_x -\frac{c}{2}x^2-\rho \gamma x-x\rho\frac{\ell}{2}\times (-I) - (1-\rho x)(1-\rho x -I)\times\frac{\ell}{2}.

Relative to all trading with intermediaries

  • Contact mass x of investors such that 

MC of contacting mass x = MC of trading Q-   x with the intermediaries

\rho
ρ\rho
cx+ \rho\gamma + \rho\frac{\ell}{2}\times (-I) =\rho \ell (Q-\rho x )+ \frac{\rho\ell}{2}\times (-I)
cx+ργ+ρℓ2×(−I)=ρℓ(Q−ρx)+ρℓ2×(−I)cx+ \rho\gamma + \rho\frac{\ell}{2}\times (-I) =\rho \ell (Q-\rho x )+ \frac{\rho\ell}{2}\times (-I)

data cost

price per unit

MC with 0 inventory

add'l cost due to non-0 inventory

validation cost

Relative to Benchmark with all trading intermediaries

  • Intermediaries' inventory adds a constant to both MCs.
  • The optimal mass of traders to contact x* is independent of the intermediaries inventories/public price.
  • Mass x* depends on:
    •   : probability of small traders accepting the offer
    •   : the (il-)liquidity of the intermediated market
    •   : complexity/data processing costs.
\rho
ρ\rho
x^*=\frac{\ell \rho}{\ell \rho^2+c} - \frac{\rho\gamma}{\ell \rho^2+c}
x∗=ℓρℓρ2+c−ργℓρ2+cx^*=\frac{\ell \rho}{\ell \rho^2+c} - \frac{\rho\gamma}{\ell \rho^2+c}
\ell
ℓ\ell
c
cc
  • Note: For small validation cost,              , holds that                                         trade with both continuum & intermediaries
0<\rho x^* < 1~\to
0<ρx∗<1 →0<\rho x^* < 1~\to
\gamma < \ell
γ<ℓ\gamma < \ell

not the main focus here, but yields a neat insight later-on

for equilibrium payoff use

\pi^\mathsf{c}(1,I)
πc(1,I)\pi^\mathsf{c}(1,I)

Peer to Peer Setting II:
Transparent & concentrated ownership

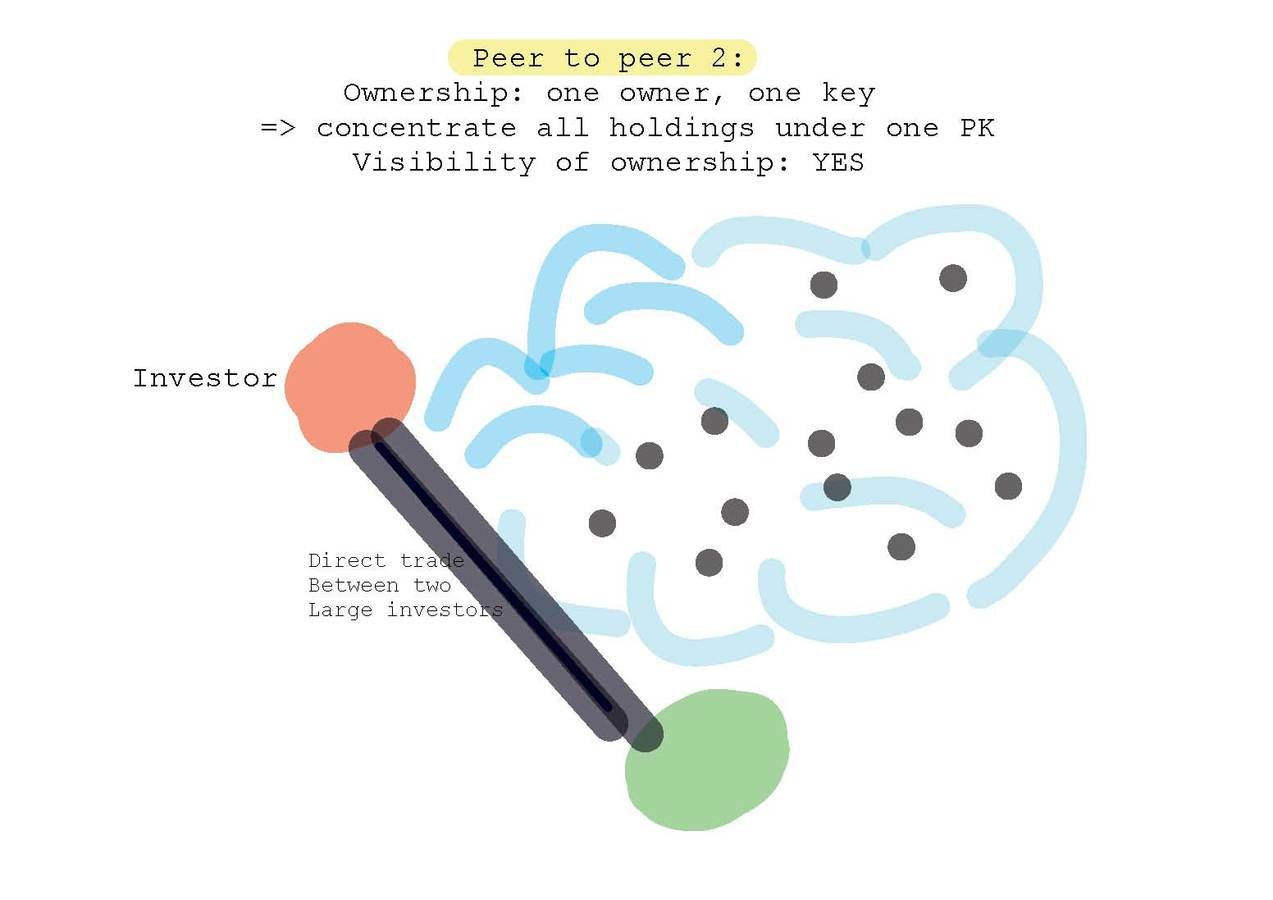
Requires a system design choice: allow an entity (individual, investment fund) only a single ID per instrument

Setting II: Transparent, concentrated Ownership

  • Key difference: Large traders are identifiable.

  • Large trader LT may:

    • Trade as in Setting I (small inv. & interm).

    • Approach the other large trader LP.

  • Search for equilibrium where LT trades with LP. 

 

Pros and Cons of Ownership Transparency

  • (+) ability to locate/contact the LP

    • escape complexity and validation costs,

    • avoid price impact of trade with risk-averse intermediaries.

  • (-) reveal info about the trading needs
    • [model choice]: LT may get “front-run” by LP.

​

Front-Running

  • Modelling Mechanics of Front-Running:
    1. LT to LP: Buy quantity Q at price p?
    2. LP buys Q from intermediary and moves the "public price" P to
    3. LP to LT: "sell you Q at price ≫ p?"
P+ \ell/2 \times Q
P+ℓ/2×QP+ \ell/2 \times Q

LT's thinking

  • Option 1: contact other large, offer p
    • ​today: pay 1 x p
    • tomorrow:
      • pay p again if shocked
      • receive p if other shocked
      • => add to zero
  • Option 2: deviate an contact the continuum
    • ​today: receive 
    • tomorrow:
      • receive              if shocked
      • receive   0         if other shocked
\pi^\mathsf{c}(1,0)
πc(1,0)\pi^\mathsf{c}(1,0)
\pi^\mathsf{c}(1,0)
πc(1,0)\pi^\mathsf{c}(1,0)
\text{FV(trigger)}=\frac{1}{2}\pi^\mathsf{c}(1,0)+\delta\times \text{FV(trigger)}
FV(trigger)=12πc(1,0)+δ×FV(trigger)\text{FV(trigger)}=\frac{1}{2}\pi^\mathsf{c}(1,0)+\delta\times \text{FV(trigger)}
~~\Leftrightarrow~~\text{FV(trigger)}=\frac{1}{2}\frac{1}{1-\delta}\pi^\mathsf{c}(1,0)
  ⇔  FV(trigger)=1211−δπc(1,0)~~\Leftrightarrow~~\text{FV(trigger)}=\frac{1}{2}\frac{1}{1-\delta}\pi^\mathsf{c}(1,0)
\Pi^{\text{LT}}(\text{deviate})=\pi^\mathsf{c}(1,0)+\delta\times \text{FV(trigger)} =\pi^\mathsf{c}(1,0)\left(1+\frac{1}{2}\frac{\delta}{1-\delta}\right)
ΠLT(deviate)=πc(1,0)+δ×FV(trigger)=πc(1,0)(1+12δ1−δ)\Pi^{\text{LT}}(\text{deviate})=\pi^\mathsf{c}(1,0)+\delta\times \text{FV(trigger)} =\pi^\mathsf{c}(1,0)\left(1+\frac{1}{2}\frac{\delta}{1-\delta}\right)

What's the future value?

LT's thinking

So in equilibrium, LT contacts the other if

p\le-\pi^\mathsf{c}(1,0)\left(1+\frac{1}{2}\frac{\delta}{1-\delta}\right)
p≤−πc(1,0)(1+12δ1−δ)p\le-\pi^\mathsf{c}(1,0)\left(1+\frac{1}{2}\frac{\delta}{1-\delta}\right)

Possibility of Front-Running

  • Single shot: LP always extracts all surplus (or would front-run). 
  • In repeated setting: 
    • Front-running is punished in subsequent periods via “trigger strategy” punishment:
    • Deviation → large traders avoid each other; trade as in Setting I forever.
  • Is it realistic? I.e., can we assume memory of deviations, repeated interactions?
    • Most peer-to-peer e-commerce systems have bilateral rating:
      • Ebay, Uber, Airbnb, etc.
    • Also doesn't have to be "personal" - "avoiding large" can just become a social equilibrium

LP's thinking

  • Option 1: contact other large, offer p
    • ​today: receive p
    • tomorrow:
      • pay p if shocked
      • receive p if other shocked
      • => adds to zero
  • Option 2: deviate and front-run
    • ​today: extract rents 
    • tomorrow:
      • receive              if shocked
      • receive   0         if other shocked
-\pi^\mathsf{c}(1,0)
−πc(1,0)-\pi^\mathsf{c}(1,0)
\pi^\mathsf{c}(1,0)
πc(1,0)\pi^\mathsf{c}(1,0)
p\ge\pi^\mathsf{c}(1,0)\left(-1+\frac{1}{2}\frac{\delta}{1-\delta}\right)
p≥πc(1,0)(−1+12δ1−δ)p\ge\pi^\mathsf{c}(1,0)\left(-1+\frac{1}{2}\frac{\delta}{1-\delta}\right)

To not have front-running, must have

The Benchmark Equilibrium

  1. In a repeated game, "social norms" have bite and front-running can always be avoided.
  2. LT always trades with LP.
  3. LT and LP share the cost savings.
  4. Price concession
    • For small discount factor (≈ infrequent interaction) price concession is necessary.
    • For large enough discount factors (≈ frequent interactions), price concession = 0 is an equilibrium.

Peer to Peer Setting III:
(Non-)Transparent & dispersed ownership

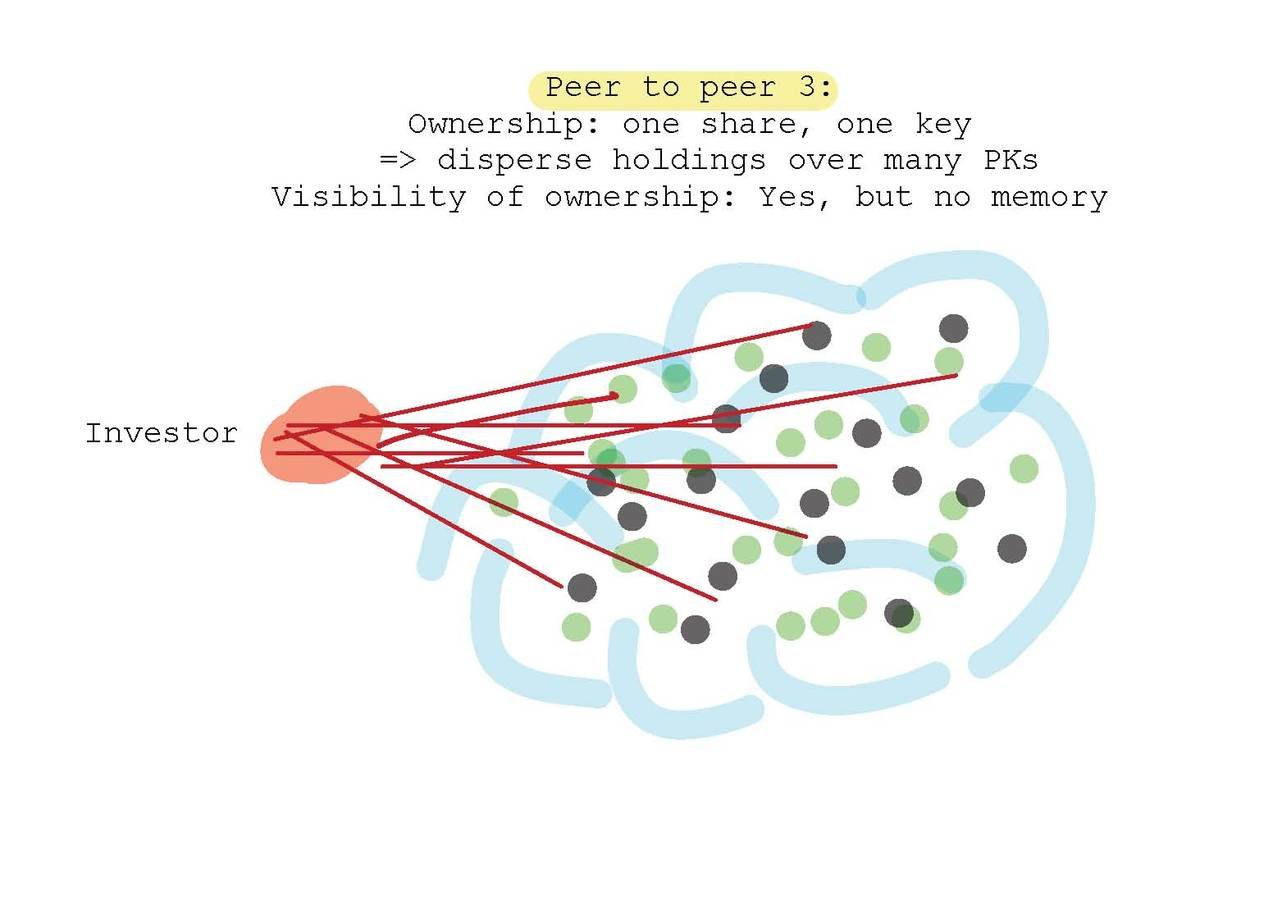
Closest and intrinsic to "public" blockchains:

  • anyone can participate anonymously
  • can create as many accounts as I want
  • describe by Ethereum founder as simple solution to achieve privacy
  • private blockchains can choose to organize themselves like this

Acceptance Probabilities

small traders

large trader

small traders

large trader

small traders

large trader

filled

unfilled

Setting I:
non-transparent, single IDs

Setting III: large accept

Setting III: large reject

\rho
ρ\rho
\frac{2\rho}{1+\rho}
2ρ1+ρ\frac{2\rho}{1+\rho}
\frac{\rho}{1+\rho}
ρ1+ρ\frac{\rho}{1+\rho}
  • LT offers p = 0 to the continuum.
  • Large trader public keys reject.
\frac{2\rho}{1+\rho} > \rho > \frac{\rho}{1+\rho}
2ρ1+ρ>ρ>ρ1+ρ\frac{2\rho}{1+\rho} > \rho > \frac{\rho}{1+\rho}

continuum & large accepts

setting I: non-transparent

continuum & large rejects

"over-trade" with the intermediary

Trigger Strategy:

Characterizing the Equilibrium

  • Search for equilibrium where LP accepts offers & doesn't front-run.
  • to avoid front-running price concession p>0 may be necessary
    • need to offer p to all peers, large and small.
  • validation costs:
    • do not affect the LT directly: with dispersed ownership, has to pay both for trades with peers and with intermediary.
    • matter for front-runner => has to pay unrecoverable sunk cost to move price
\pi^\mathsf{da}(p)
πda(p)\pi^\mathsf{da}(p)

Payoff called

x^\mathsf{da}(p)
xda(p)x^\mathsf{da}(p)

quantity 

Characterizing the Equilibrium

  • Trigger strategy LT:
    • Offer p=0 to continuum
    • go straight to intermediary and "overtrade"
  • Response LP:
    • always reject offer of p=0
\pi^\mathsf{dr}(0)
πdr(0)\pi^\mathsf{dr}(0)

Payoff called

Decision problem LT

accept offer

submit large amount to continuum

  • (small) price concession to entice larger trader (but also paid and wasted on small traders)
  • larger search costs
  • no price concession
  • expensive interaction with intermediary
  • smaller search cost

Decision problem LP

submit large amount to continuum

front run

  • small wrinkle: may involves paying settlement fee when front-running

Condition for LT

\pi^\mathsf{da}(p)+\frac{1}{2}\frac{\delta}{1-\delta}\left(\frac{px^\mathsf{da}}{1+\rho^{-1}}+\pi^\mathsf{da}(p)\right)\ge\pi^\mathsf{dr}(0)+\frac{1}{2}\frac{\delta}{1-\delta}~\pi^\mathsf{dr}(0)
πda(p)+12δ1−δ(pxda1+ρ−1+πda(p))≥πdr(0)+12δ1−δ πdr(0)\pi^\mathsf{da}(p)+\frac{1}{2}\frac{\delta}{1-\delta}\left(\frac{px^\mathsf{da}}{1+\rho^{-1}}+\pi^\mathsf{da}(p)\right)\ge\pi^\mathsf{dr}(0)+\frac{1}{2}\frac{\delta}{1-\delta}~\pi^\mathsf{dr}(0)

declines in p

Condition for LP

\frac{px^\mathsf{da}}{1+\rho^{-1}}+\frac{1}{2}\frac{\delta}{1-\delta}\left(\frac{px^\mathsf{da}}{1+\rho^{-1}}+\pi^\mathsf{da}(p)\right) \ge\ell\times \left(\frac{x^\mathsf{da}}{1+\rho^{-1}}\right)^2+\frac{1}{2}\frac{\delta}{1-\delta}\pi^\mathsf{dr}(0)- \frac{\gamma x^\mathsf{da}}{1+\rho^{-1}}
pxda1+ρ−1+12δ1−δ(pxda1+ρ−1+πda(p))≥ℓ×(xda1+ρ−1)2+12δ1−δπdr(0)−γxda1+ρ−1\frac{px^\mathsf{da}}{1+\rho^{-1}}+\frac{1}{2}\frac{\delta}{1-\delta}\left(\frac{px^\mathsf{da}}{1+\rho^{-1}}+\pi^\mathsf{da}(p)\right) \ge\ell\times \left(\frac{x^\mathsf{da}}{1+\rho^{-1}}\right)^2+\frac{1}{2}\frac{\delta}{1-\delta}\pi^\mathsf{dr}(0)- \frac{\gamma x^\mathsf{da}}{1+\rho^{-1}}

front-running is costly = sunk cost of validation

Equilibrium & More

Result 1: There exists an equilibrium with no front-running where

  • LP accept
  • price concession = 0

provided

  • the discount factor is large enough
    • = frequent interactions.
  • or the intermediated market is sufficiently liquid
    • = front running not very profitable (small quantity and low price advantage)
  • or validation costs are sufficiently high
    • = sunk cost for front-running too high.

Equilibrium & More

Result 2 (numerical): For small discount (=infrequent interaction) factors, the equilibrium with no front-running where LP accept does not exist. Then:

  • In equilibrium, LT offers p = 0 to the continuum, and
  • LP's IDs reject the offer.
     

=> over-trading with intermediary

 

 

Comparing the three designs

Payoffs with transparent, concentrated ownership are highest.

  • Large interact 
    • => no complexity costs
    • => no intermediation costs
    • => no validation costs
  • Social norms have the strongest bite when there is full transparency.

Comparing the three designs

Observations

  • trading with the intermediary is socially inefficient 
    • to avoid this cost, large traders must interact
    • if not, there is always an imbalance of traders who trade with the intermediary
  • trades between small and large traders cause complexity costs
  • Thus trade-off for large trader interaction is
    • complexity cost vs
    • intermediation cost

Comparing the three designs

What determines welfare?

  1. complexity costs + amount with continuum
  2. for large: amount traded with intermediary
  3. for small: amount that large traded with intermediary

depend on acceptance probability

depends on whether large trade with large

\tilde{x}
x~\tilde{x}
\tilde{\rho}
ρ~\tilde{\rho}
\tilde{p}
p~\tilde{p}
W(\tilde{x},\tilde{\rho},\tilde{p})=-\frac{c}{2}\ \tilde{x}^2-\frac{\ell}{2} (1-\tilde{\rho}\tilde{x})^2-\frac{\ell}{2}\ \tilde{p}\tilde{\rho}\tilde{x}\ (\tilde{p}\tilde{\rho}\tilde{x}-(\tilde{\rho}\tilde{x}-1))
W(x~,ρ~,p~)=−c2 x~2−ℓ2(1−ρ~x~)2−ℓ2 p~ρ~x~ (p~ρ~x~−(ρ~x~−1))W(\tilde{x},\tilde{\rho},\tilde{p})=-\frac{c}{2}\ \tilde{x}^2-\frac{\ell}{2} (1-\tilde{\rho}\tilde{x})^2-\frac{\ell}{2}\ \tilde{p}\tilde{\rho}\tilde{x}\ (\tilde{p}\tilde{\rho}\tilde{x}-(\tilde{\rho}\tilde{x}-1))

Comparing concentrated vs dispersed

 

  • Equilibrium 1: Large don't trade with one another
    • acceptance probability is lower
    • large don't interact
    • interaction with intermediary vs. continuum not immediately obvious
      • possibly contact more continuum (higher complexity cost)
      • but find fewer matches (lower costs for small)
    • Overall result:
      • total welfare with concentrated and dispersed ownership is identical

Comparing concentrated vs dispersed

 

  • Equilibrium 2: Large trade with one another
    • ​Acceptance probability is higher and
    • Large interact
      • increases welfare
    • ​​price concessions are zero-sum but change behavior 
  • Overall result
    • total welfare with  dispersed ownership is unambiguously higher
  • Insight: ability to tap into latent, undisplayed liquidity always helps, even if there are search costs and externalities.

Influence of Validation Cost

For dispersed ownership, there exist parametric configurations s.t. 

small increase in validation cost => increase in aggregate payoff   

Idea: Switch from

  • "trigger" equilibrium =
    • no price concession
    • LP rejects
    • overtrade with intermediary 
  • to "co-operate" equilibrium 
    • offer price concession (good for small!)
    • LP accepts

Summary

  1. Known design choices for Blockchains/DLT
    • public vs. private
    • permissioned vs. permissionless
  2. Our paper:
    • "back office" settlement has important front office implications!
    • with peer-to-peer there are further critical design choices
      • Who can see the ledger?
      • How are virtual identities managed?
      • Loose insight: if you enable peer-to-peer, do it do that people can find each other.
  3. Let’s start talking about market design with blockchain technology!
    • several blockchain exchanges already operate (e.g., LykkeX, Godzillion).
    • Overstock.com together with t0 will allow blockchain-based trading by end-2017.
    • NASDAQ has issued securities using Blockchain tech.
    • DTCC will soon offer some form of blockchain settlement.
    • ASX in Australia will soon settle on a blockchain.

Final Thoughts

  1.  It's an economically big question.
    • HFT annual revenue: $1.3B (TABB Group estimate for 2014).
    • IT cost savings from Blockchain for FI:
      • $6B (Goldman), $20B (Santander).
      • current post-trade and securities servicing fees are ≈$100B (Oliver Wyman).
  2. The technological change can give rise to new market structures
    • Once-in-a-lifetime opportunity for reset and optimization of the organization and regulation of trading.
  3. Academic research can make important contributions to set up solid market organization.