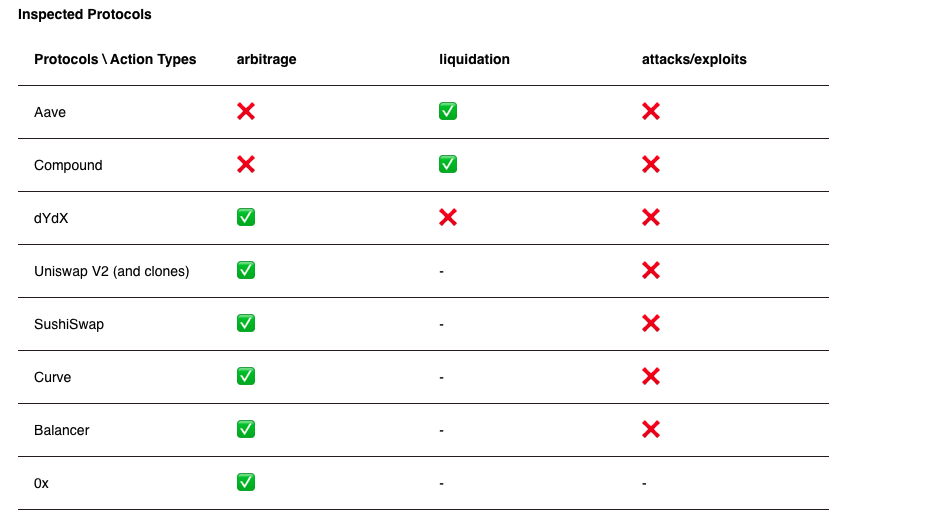
Decentralized Trading and
The Economics of AMMs
Andreas Park


Goal of this class
- ultra-brief intro to the area of market microstructure
- introduction to the analysis of decentralized trading
Why care about Decentralized Trading?
What makes DeFi different from TradFi?
- Self-custody of assets
- Access to financial infrastructure
- Conceptually non-custodial services
- Value management layer = common resource
- Platform approach to commerce
{
{
features
consequences
Traditional Markets
Trading Arrangements
central limit order book
complexity
impact of trades
anonymity
price discovery
centralized auction
bilateral
negotiation
Request
for Quote
open
outcry
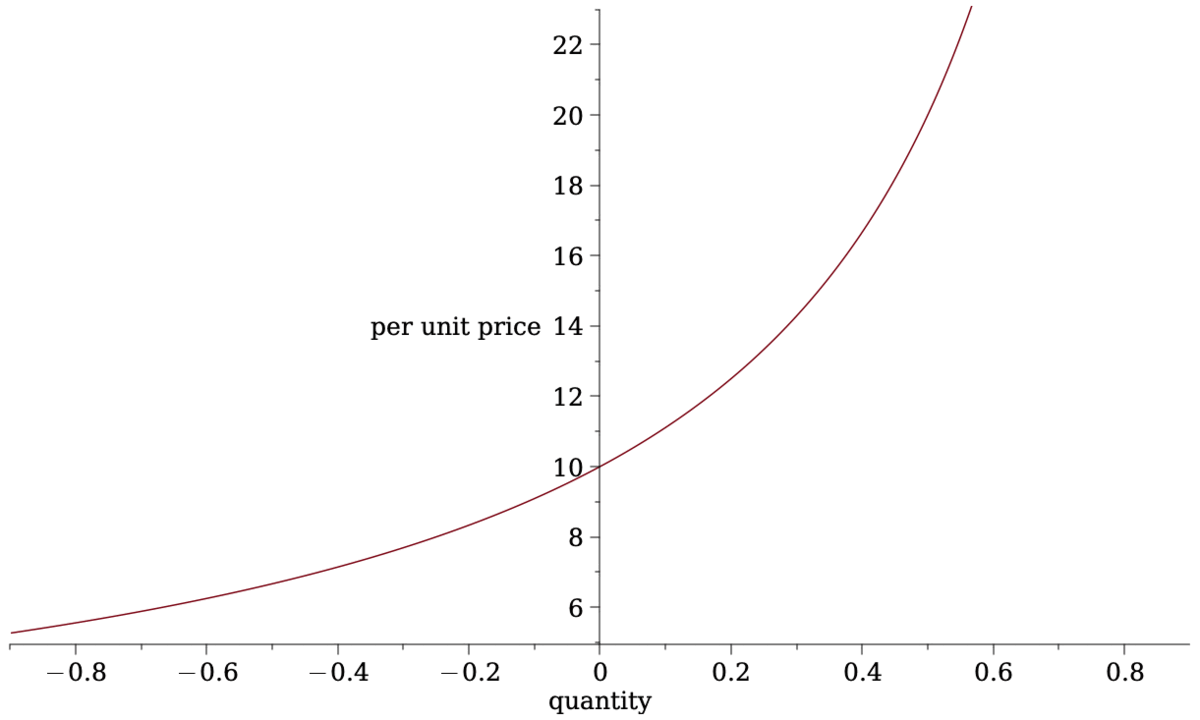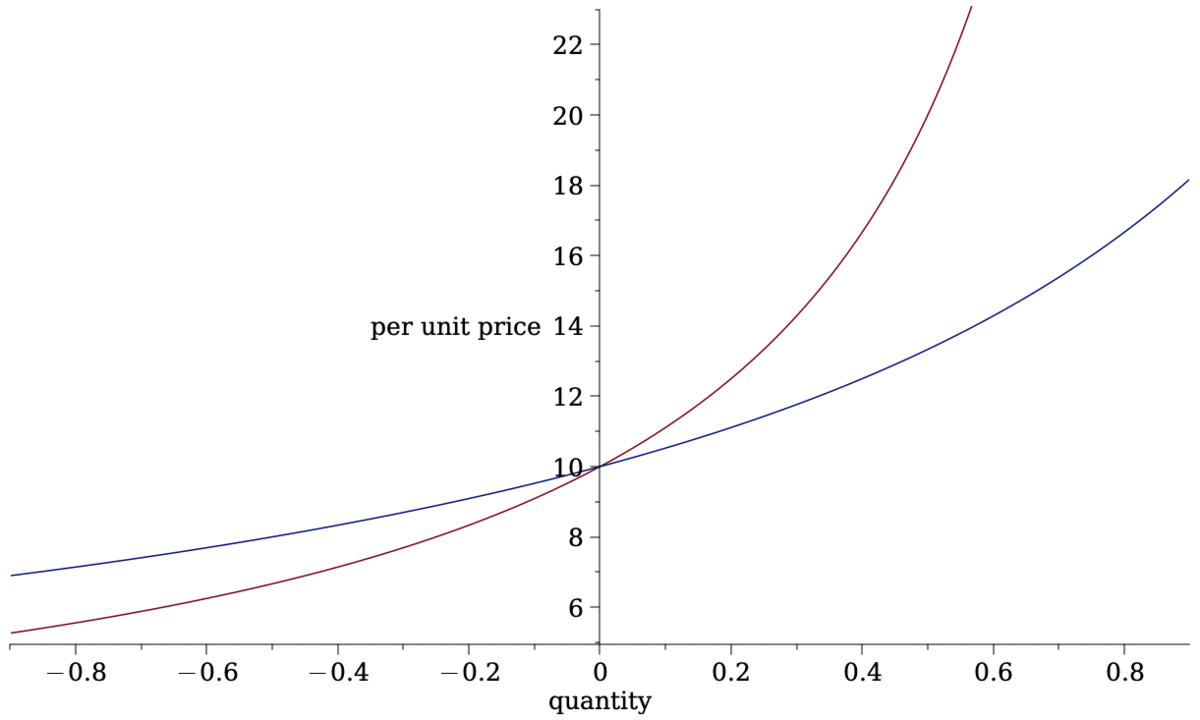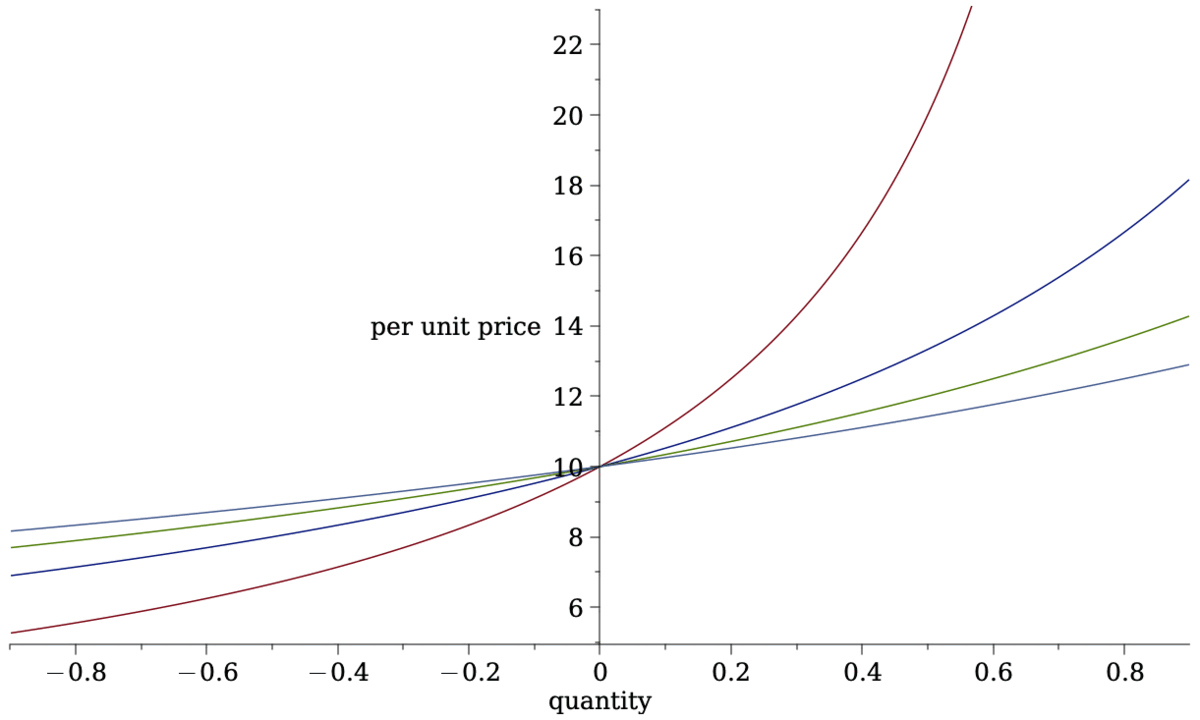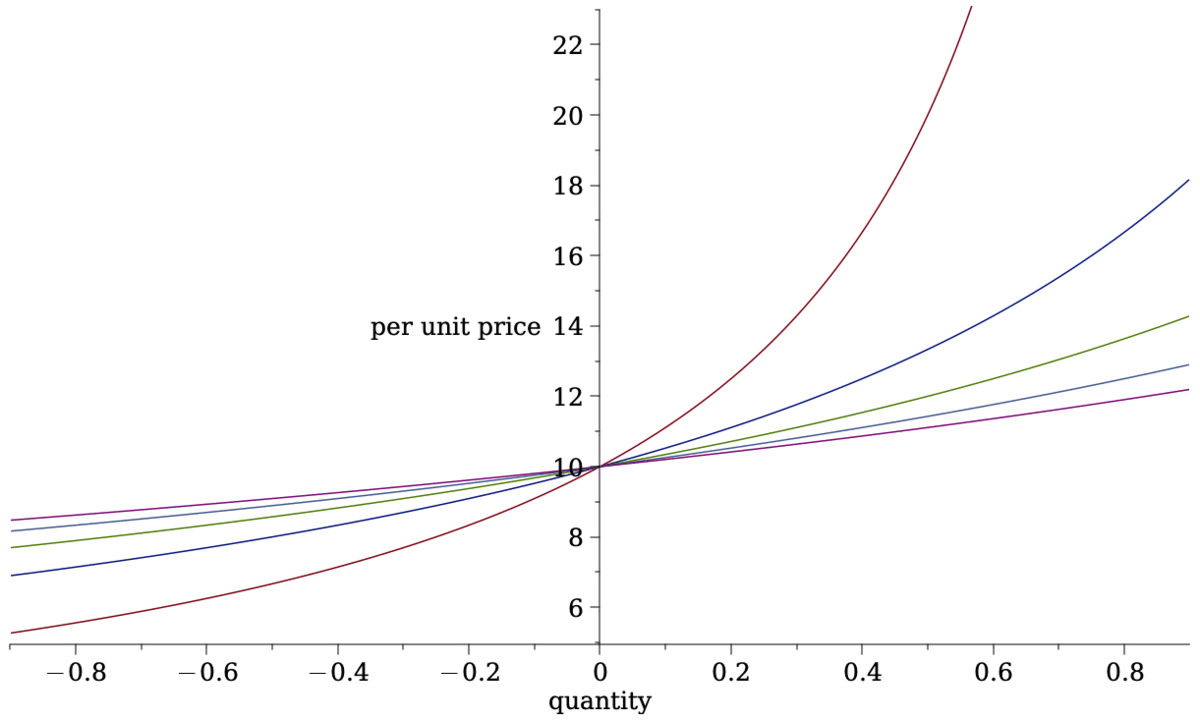
marginal pricing function
quantity \(Q\)
price \(p(Q)\)
Illustration of pricing
quantity
price
\(Q\)
\(p(Q)\)
\(P^{\mathsf{up}}(Q)=p(Q)\times Q\)
Illustration of pricing: auctions/open outcry/RFQ: uniform price
Illustration of pricing: limit order book = discriminatory pricing

quantity
price
\(Q\)
\(p(Q)\)
\(P^{\mathsf{dp}}(Q)=\int_0^Qp(q)~dq\)
Who trades?
- Most of the time there is no "coincidence of wants"
- \(\Rightarrow\) Need liquidity providers!
- What's there first?
- trader's order \(\equiv\) liquidity provision
- trader's order \(\to\) liquidity provision
- liquidity provision \(\to\) trader's orders
- Deeply affects models and modelling choices
Key question for liquidity provision
- Why is there trading?
- diversification/liquidity shocks
- private information
Basics of liquidity provision under value uncertainty
- fundamental value up
- \(\Rightarrow\) price up
- \(\Rightarrow\) sell the asset for less than its worth
- \(\Rightarrow\) price up
- fundamental value down
- \(\Rightarrow\) price up
- \(\Rightarrow\) buy the asset for more than its worth
- \(\Rightarrow\) price up
Questions:
- Are there fees/cash sources of income?
- When does/did the value change?
- When do I assess the positional gain/loss?
- liquidity provision = accept a risk
- risk = fundamental value may change (or may have already changed and you don't know it)
every model has some form of structure like
\[\text{trading fee income} +\underbrace{\text{what I sold it for}-\text{value of net position}}_{\text{positional gain/loss}} \ge 0 \]
Example 1: Grossman/Miller
- Any position is a risk \(\to\) cost
- always over-price the trade to compensate for risk
Example 2: Kyle or Glosten-Milgrom
- trade with informed:
- receive too little/pay too much
- trade with uninformed:
- pay too little/receive too much
- trade-by-trade view
- can either trade on "other" market
- hold asset to maturity
Example 3: Limit order market (a la Glosten 1994)
- trade with uninformed:
- overprice small orders
- trade with informed:
- underprice small orders
Small point:
- Regret free prices: after you see the trade, you don't want to change the price
- Kyle prices are regret free
- Limit order book prices are not regret free: large orders are more informed so you undercharge when a larger order trades against lower priced orders
Crypto Markets



















Broker


Exchange
Internalizer
Wholeseller
Darkpool


Venue



Settlement
Decentralized Trading

















... 300 lines of code ...

Trading Infrastructure
Actually ...
- bad idea
- Why?
- Data-intensive, computation intensive, costly, inefficient
Let's look at some stylized facts
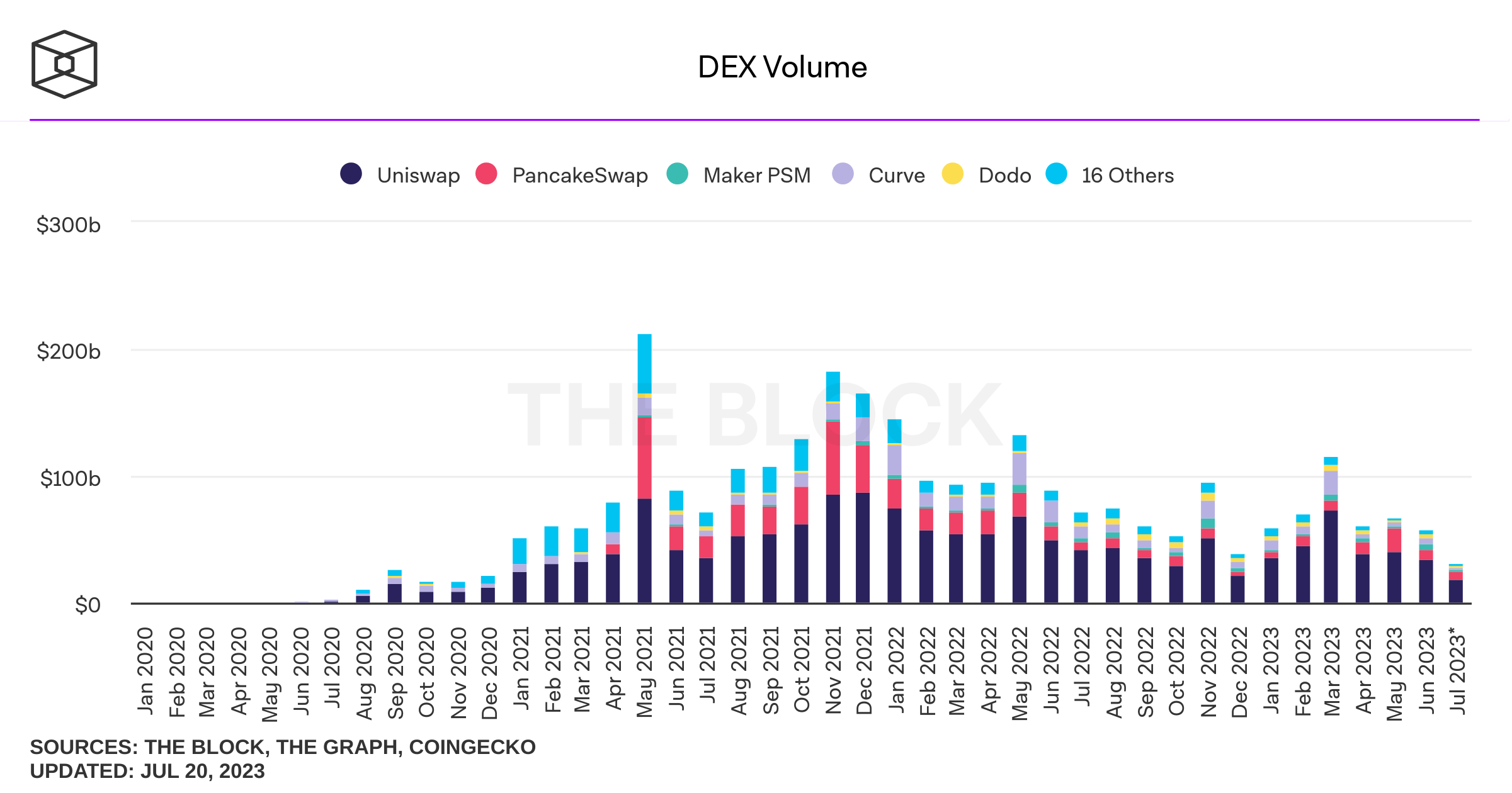
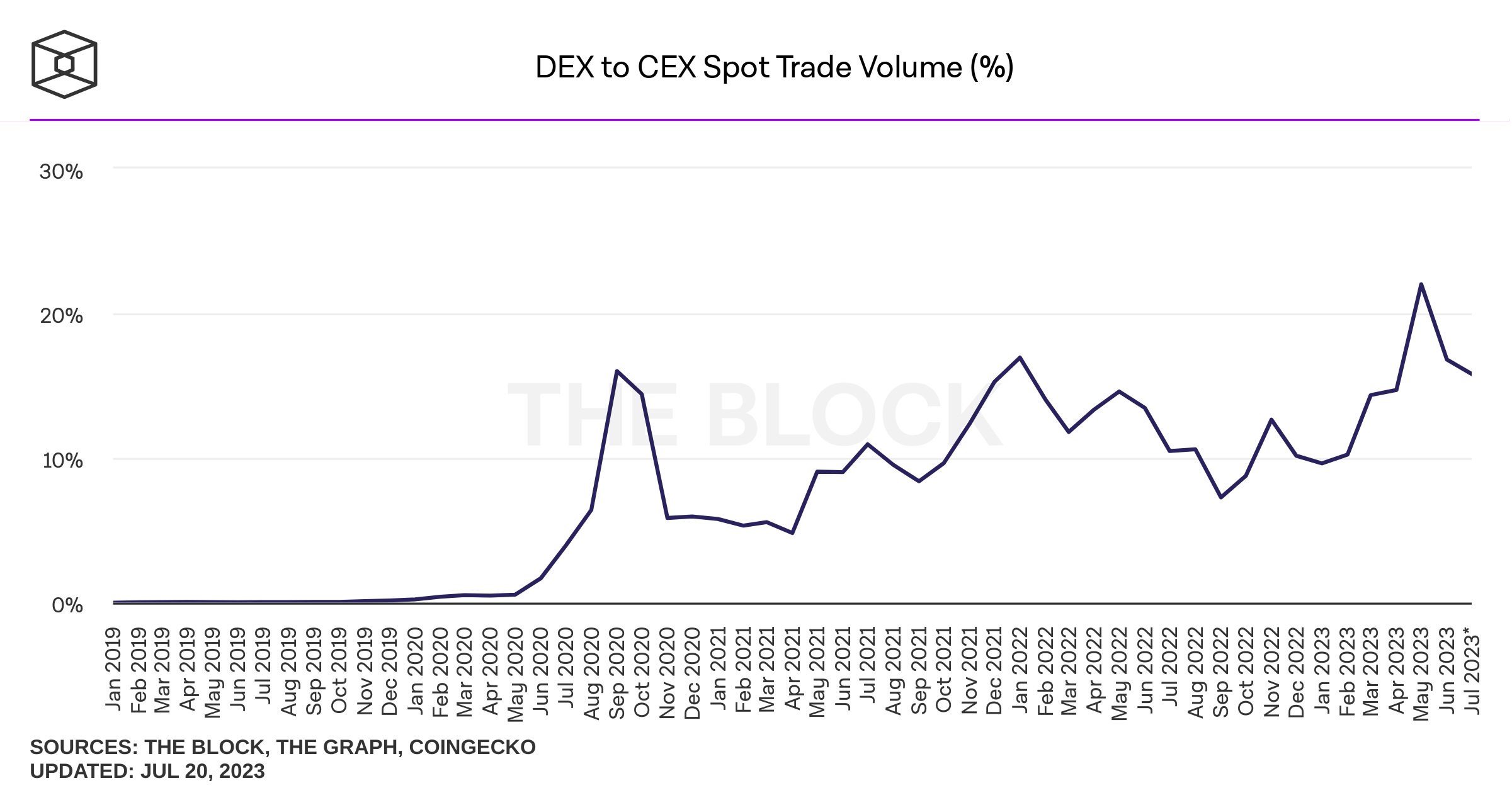
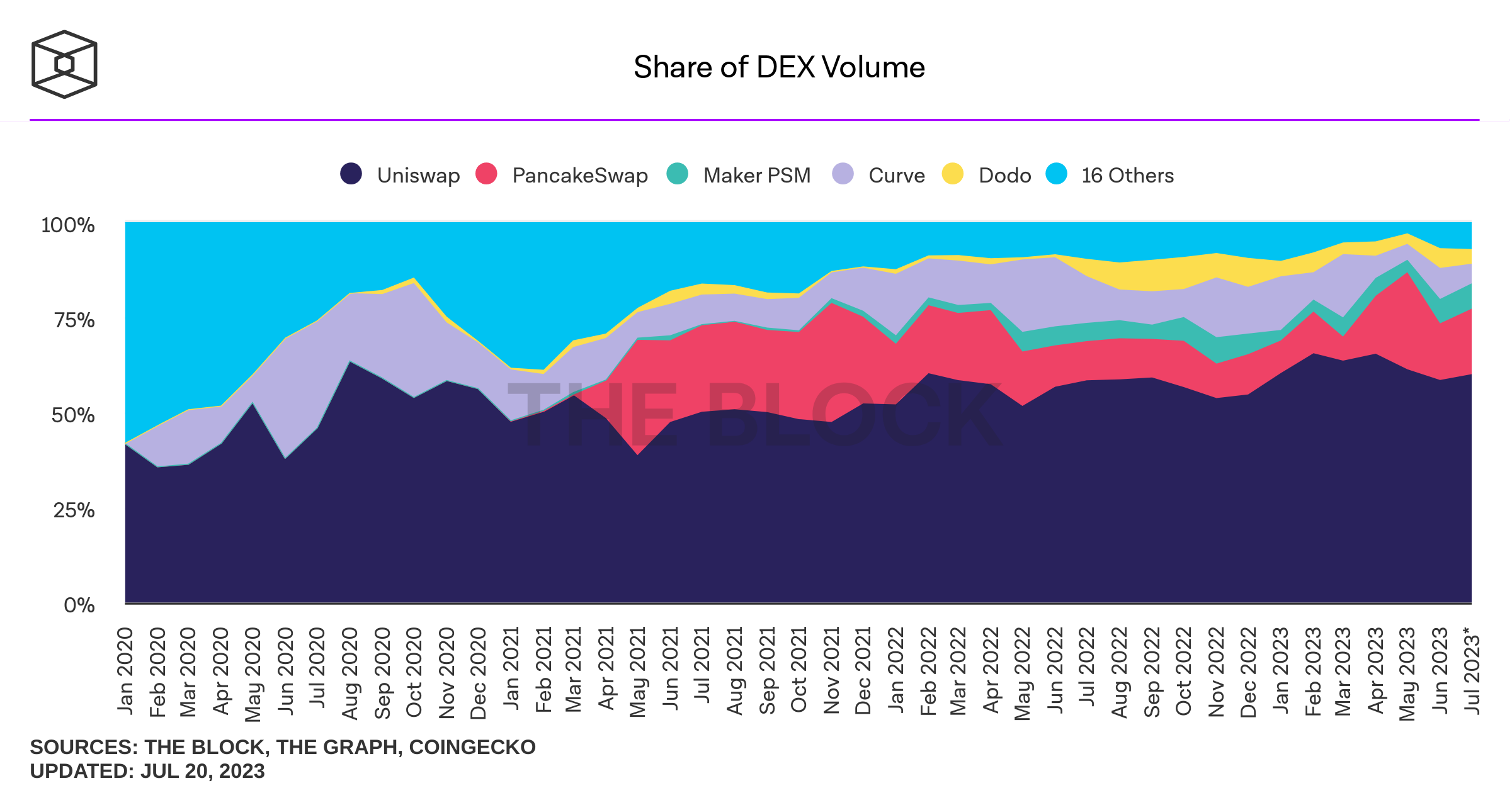
Let's look at some stylized facts
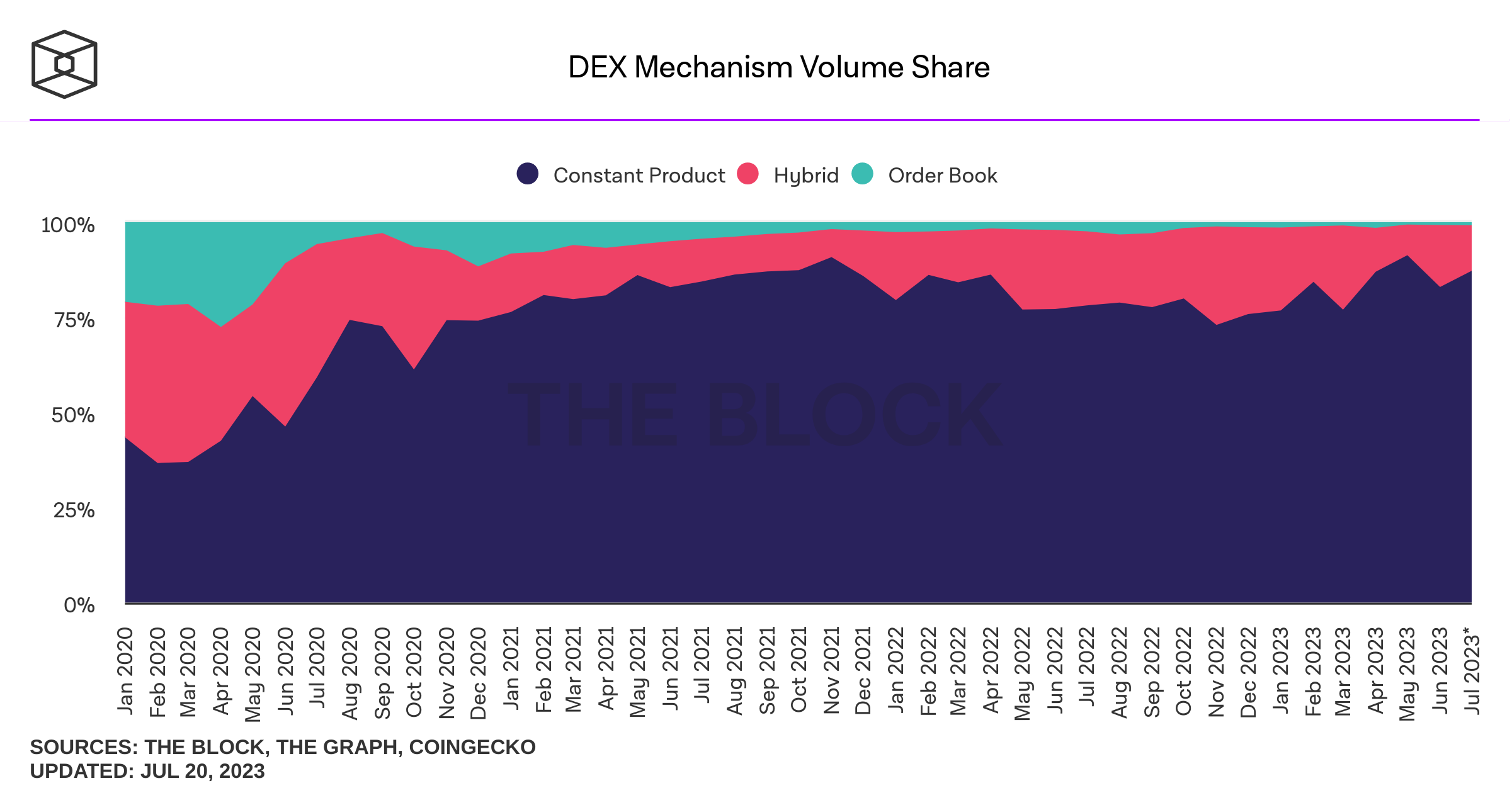
How does it look?
automated market maker


\(\to\) simply connect with MetaMask (or similar wallet)
Decentralized Trading
Decentralized trading using automated market makers (AMM)













Liquidity providers
Liquidity demander
Liquidity Pool

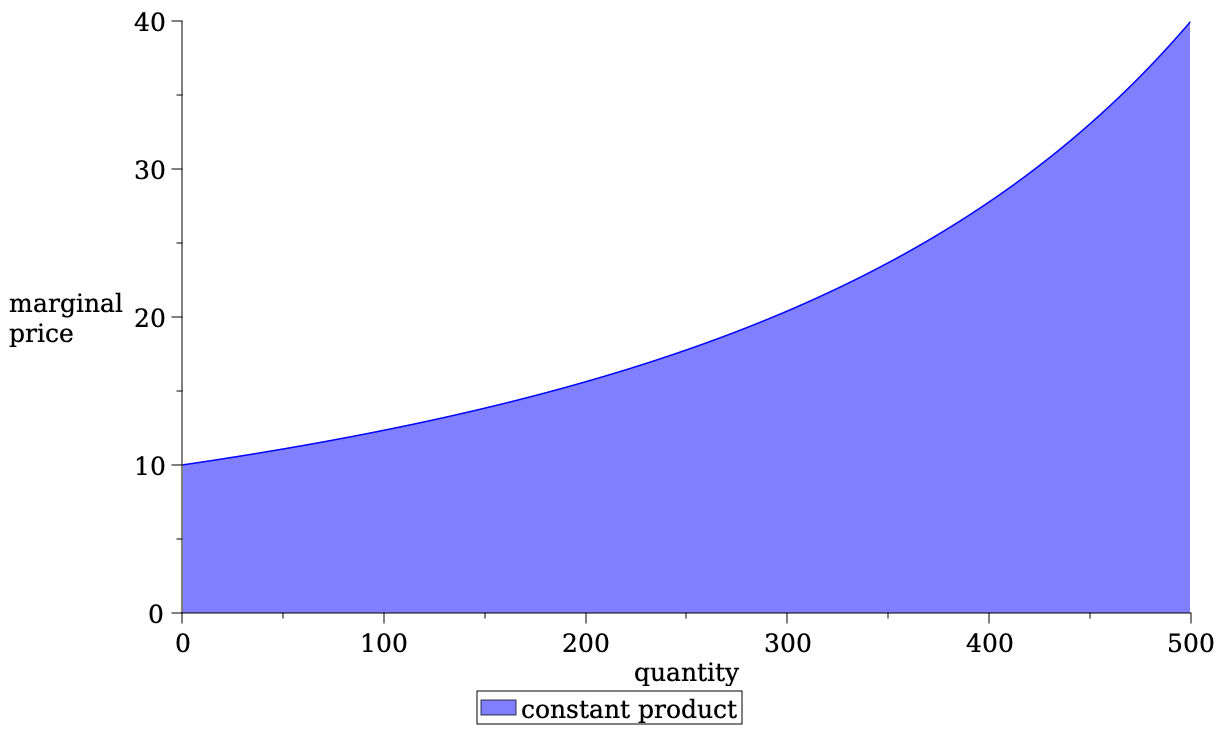
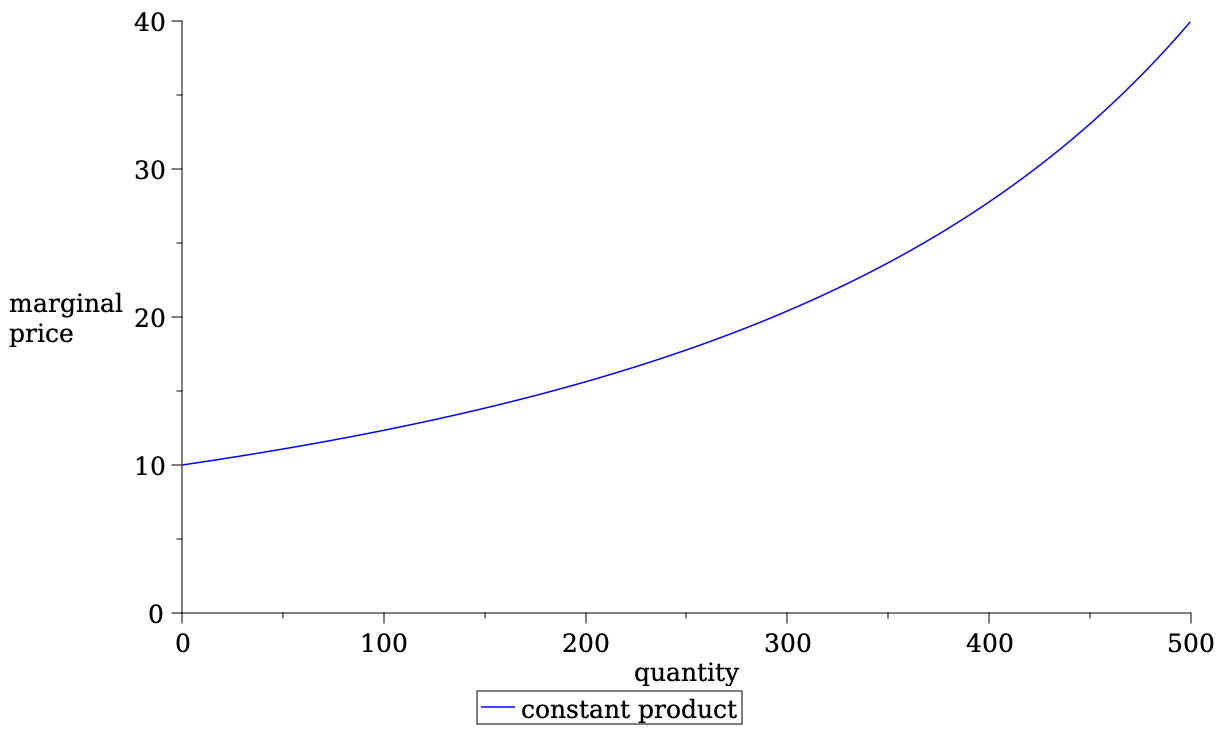
AMM pricing is mechanical:
- determined by the amounts of deposits
- most common:
- constant product
- #USDC \(\times\) #ETH = const
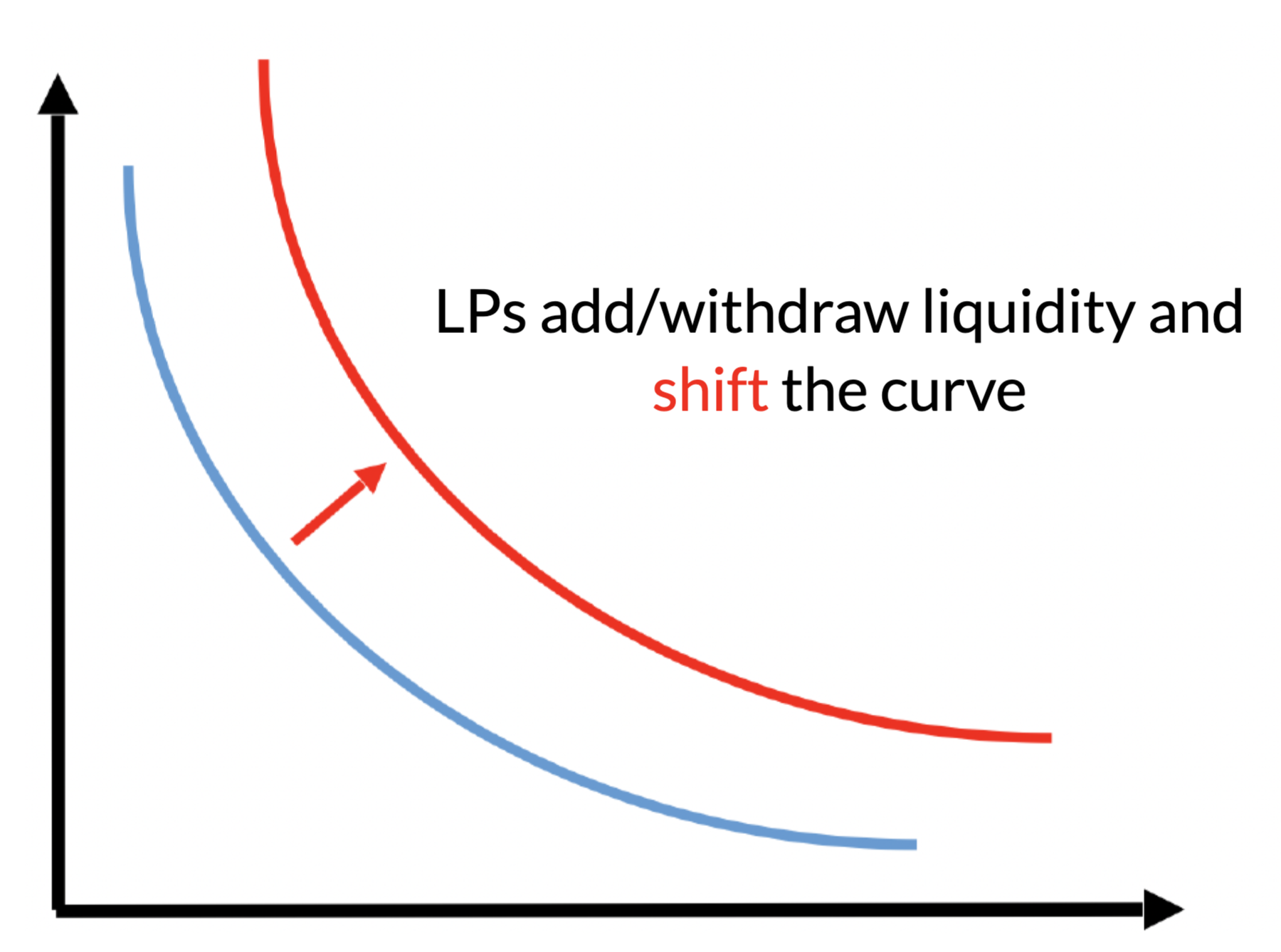
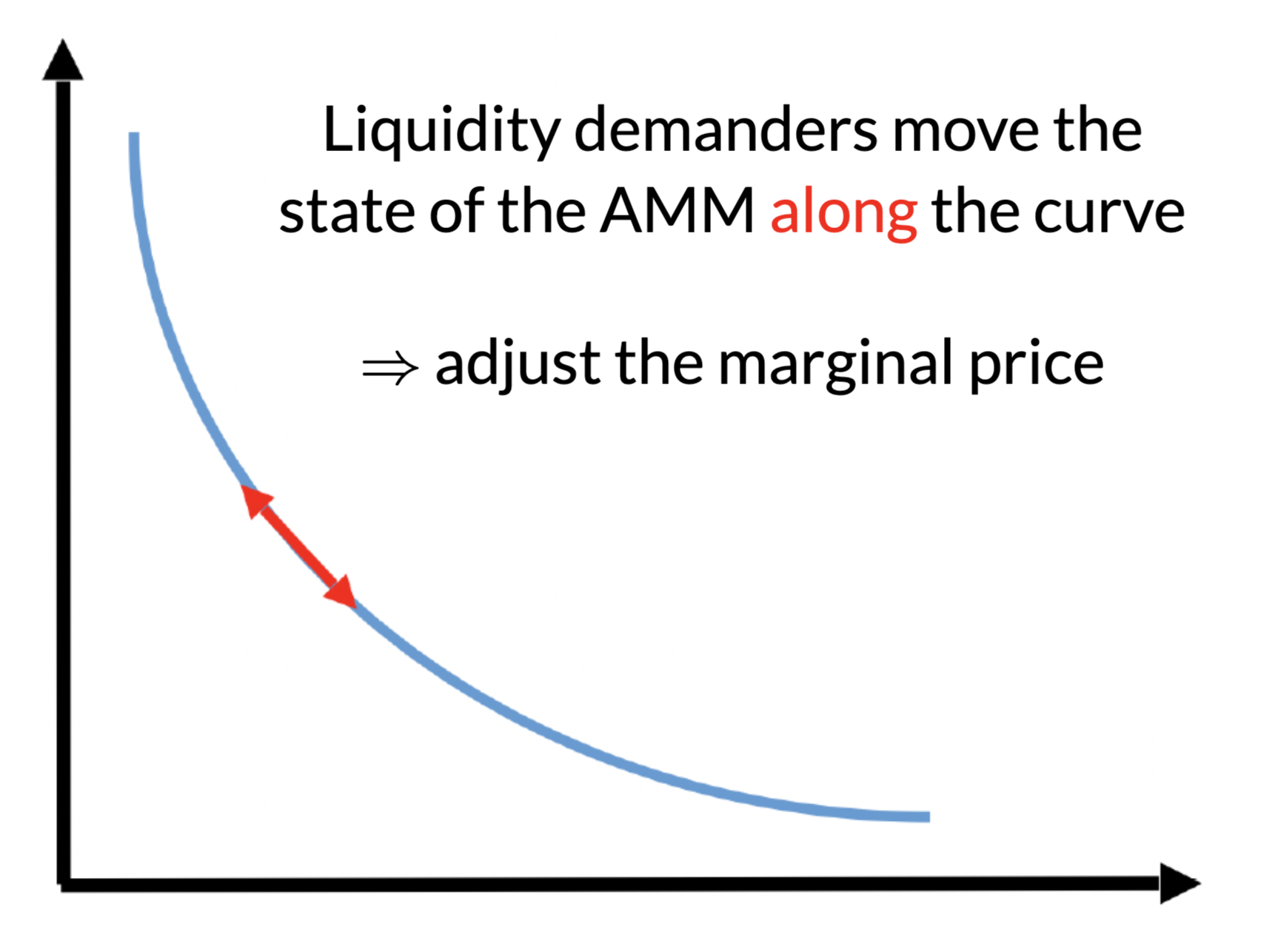
No effect on the marginal price
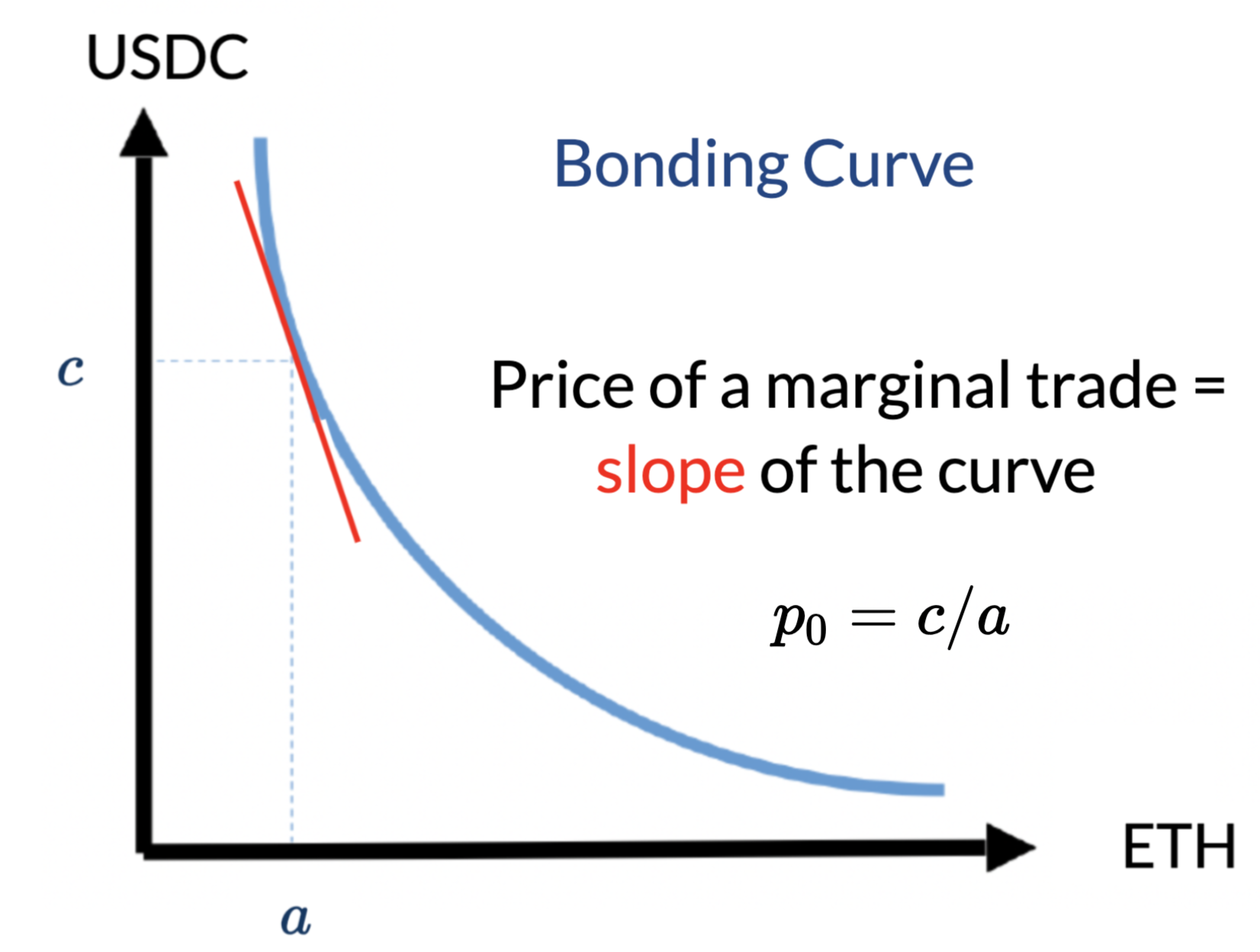
AMM Theory: Price Functions
Basic Requirements for "unconstrained" liquidity
- Two assets:
- cash and an asset
- deposits in pool of \(c\) cash and \(a\) asset
- AMMs should be self-contained: pricing rule based on
- deposits \(a,c\) and
- liquidity demanded \(q\)
- implied value of the asset at deposit: \[p=\frac{c}{a}.\]
- marginal price: an infinitesimal unit should cost \[p^m=p\]
What does an AMM need?
- trades create linear changes:
- a trade of \(q\in(-\infty,a),\) will cost \(\Delta c(q)\)
- liquidity changes
- \(a\) \(\to\) \(a-q\)
- \(c\) \(\to\) \(c+\Delta c(q)\)
- \(\to\) marginal price after trade of \(q\) is
\[p^m(0)=\frac{c}{a}~~\to~~p^m(q)=\frac{c+\Delta c(q)}{a-q}.\]
quantity
price
\(q\)
\(p^m(q)\)
\(\Delta c(q)(Q)=p(q)^m\times q\)
Traditional pricing: auctions/open outcry/RFQ: uniform price
idea: cost of \(q=\) price\(\times\) quantity
note: \(p(q)\) does not have to be linear
Some Pricing Rules from Traditional Markets: Uniform Price
- assume cost is price \(\times\) quantity: \[\Delta c(q)=q\cdot p^m(q)\]
- plus assume average price \(=\) marginal price after trade
\[p^m(q)=\frac{c+q\cdot p^m(q)}{a-q}~~\Leftrightarrow~~p^m(q)=\frac{c}{a-2q}.\]
- formalized and analyzed by Canidio and Fritsch (2023) and implemented in COW-Swap
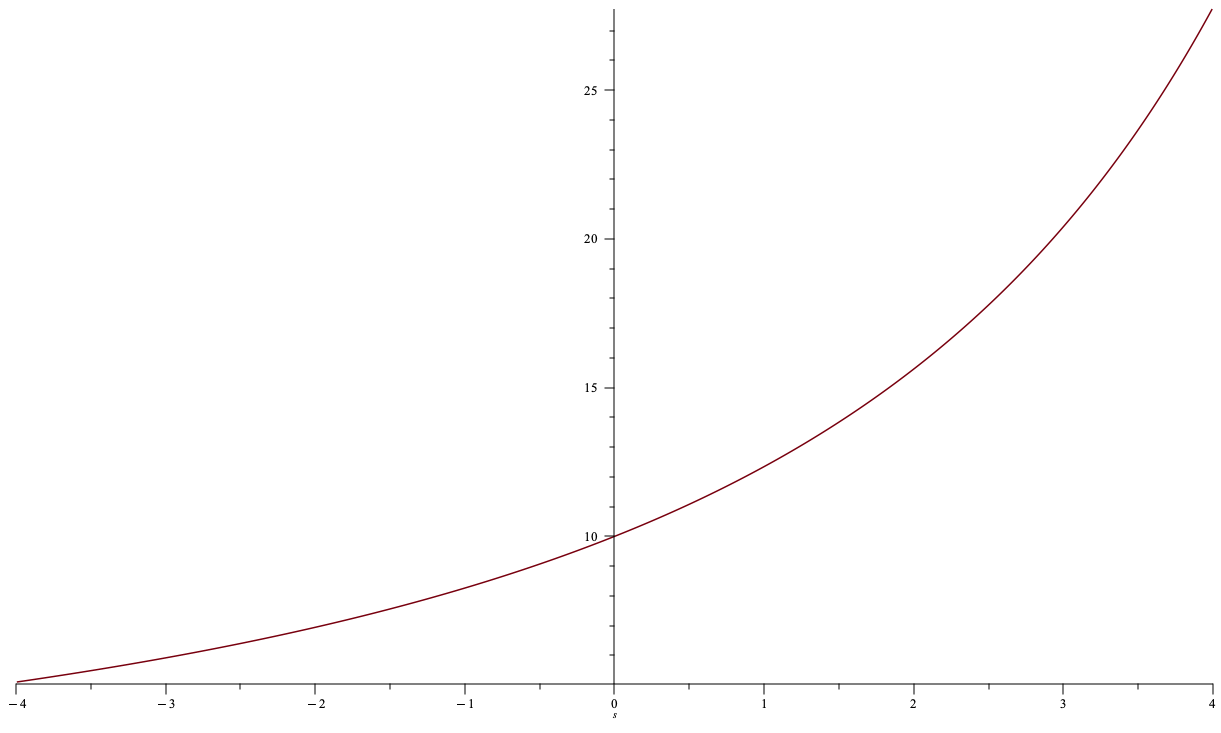
\(q=2\)
\(\Delta c(q)= q\times p^m(q)=2\times 15.5\)
Main pricing rule in stock exchanges: limit order book


quantity
price
\(q\)
\(p^m(q)\)
\(\Delta c(q)=\int_0^qp^m(s)~ds\)
again note: the marginal pricing function \(p(q)\) does not have to be linear
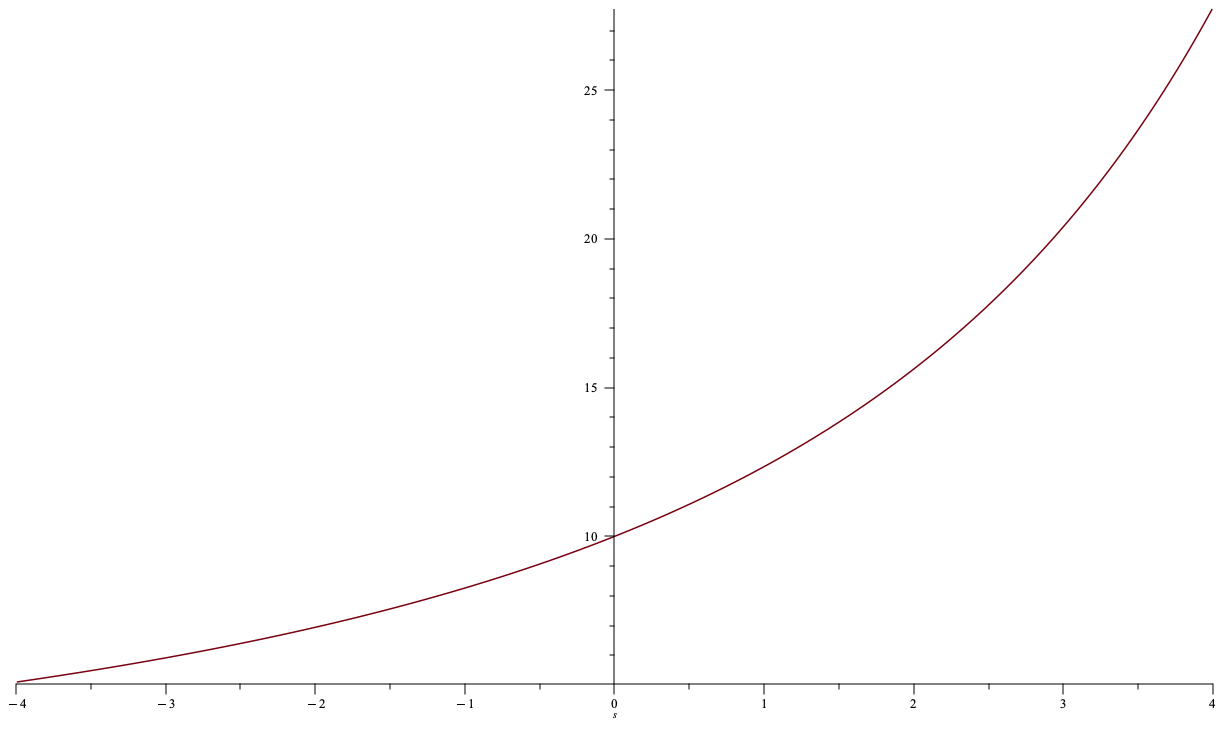
Some Pricing Rules from Traditional Markets: Limit Order Book
- For AMM: assume continuity \(\to\) price of "final" marginal unit coincides with price of "first" marginal unit of next trade \[\Delta c(q)=\int_0^q p^m(s) ds~\to~\Delta c'(q)=p^m(q).\]
- Also "first" unit costs nothing \(\Delta c(0)=0\)
- This gives us a differential equation
\[p^m(q)=\frac{c+\int_0^q p^m(s) ds}{a-q}~~\Leftrightarrow~~\Delta c'(q)=\frac{c+\Delta c(q)}{a-q},\] - with solution \[\Delta c(q)=q\cdot\frac{c}{a-q}.\]
- Or, we can write \[\Delta c(q)=\int\limits_0^q p^m(s)ds=\int\limits_0^q\frac{ac}{(a-q)^2}ds=\frac{cq}{a-q}.\]
- Idea of pricing: liquidity before trade \(=\) after trade
\[L(a,c)=L(a-q,c+\Delta c)\]
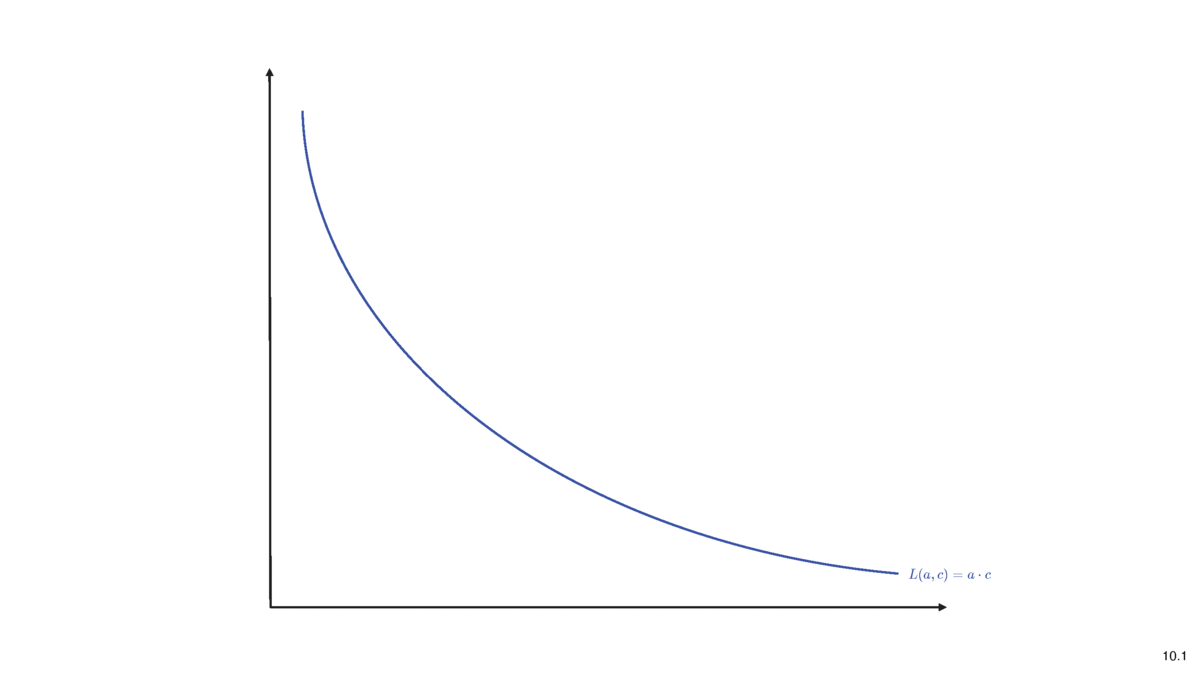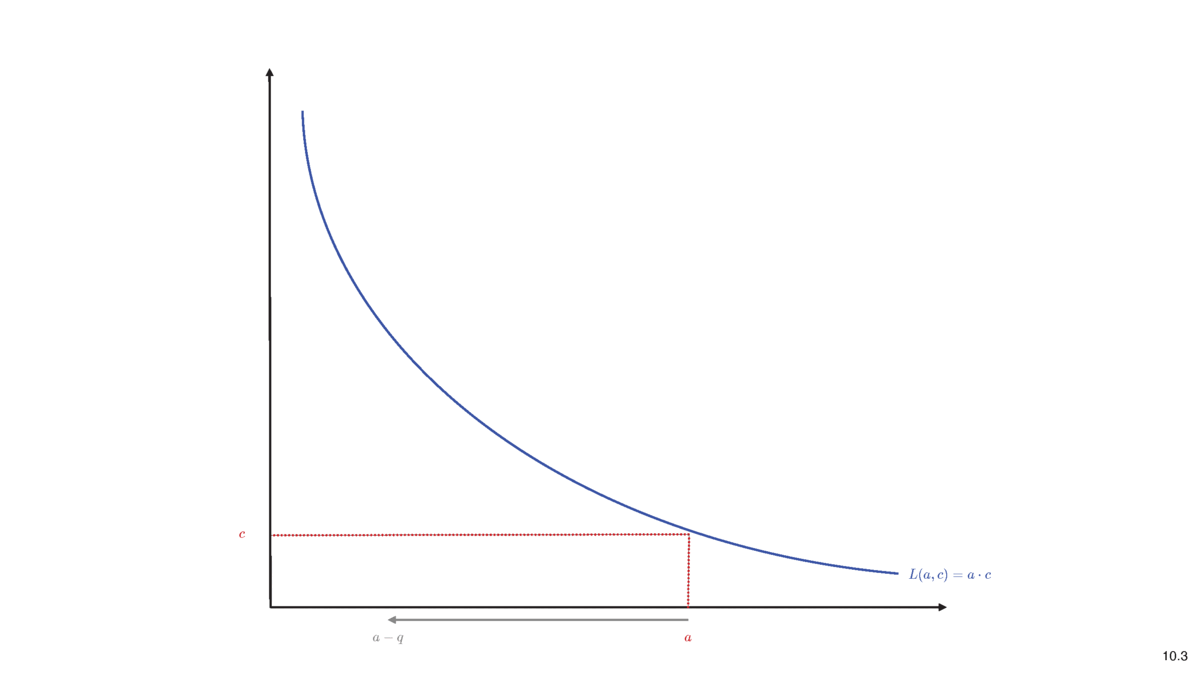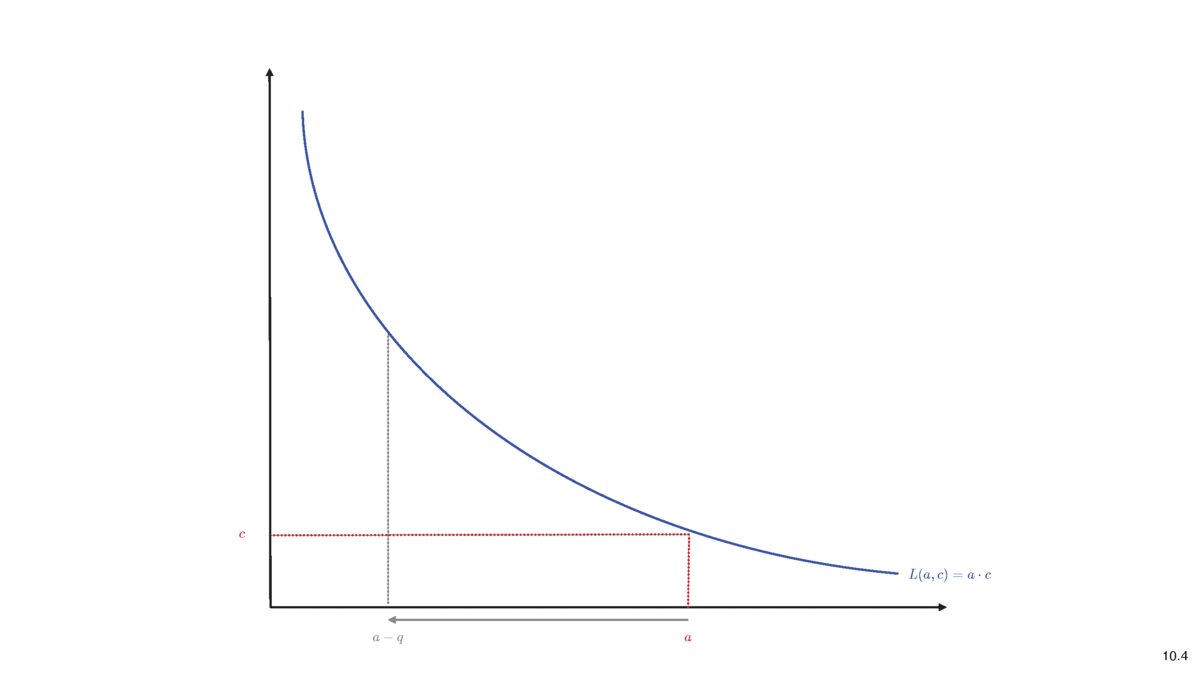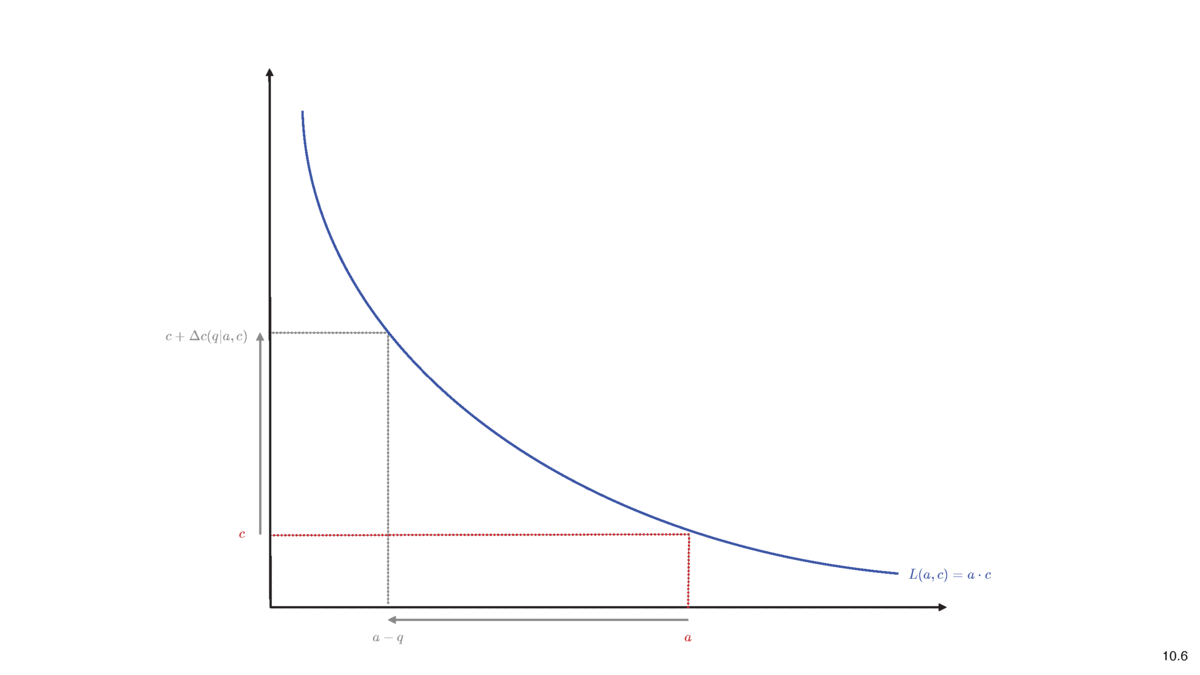
Most Common Pricing Rule in DeFi: Constant Product
Most Common Pricing Rule in DeFi: Constant Product
- With \[a\cdot c= (a-q) (c+\Delta c(q))\]
-
we compute cost \[\Delta c(q)=q\cdot \frac{c}{a-q},\]
- and marginal price \[p^m(q)=\frac{c+\frac{cq}{a-q}}{a-q}=\frac{ac}{(a-q)^2}.\]
Insight: AMM pricing function is the same as a limit order book when we require
- that prices are continuous and
- that prices are determined by liquidity deposits only
- time \(\times\) quantity: \[p(q)=\frac{c}{a-2q}\]
- limit order book: \[p(q)=\frac{c}{a-q}.\]
- constant product: \[p(q)=\frac{c}{a-q}.\]
average prices
Some insights on pricing functions
- Price \(\times\) quantity
- nice feature:
- regret-free price: if price move is due to information, you have no positional loss
- poor feature:
- you can always save by order-splitting (formally shown by Canidio and Fritsch (2023))
- limit price for splitting = limit order book price
- nice feature:
- LOB/CP
- nice feature:
- order splitting doesn't pay
- poor feature:
- prices not regret-free: if price move is due to information, you always lose
- nice feature:
The Pricing Function
- Most common form of AMM liquidity rule is Constant Product Pricing
\[L(a,c)=a\cdot c~\Rightarrow~a\cdot c= (a-q)\cdot (c+\Delta c).\] - Total cost of trading \(q\) \[\Delta c=\frac{cq}{a-q}.\]
- Price per unit \[p(q)=\frac{c}{a-q}.\]
- Average spread paid\[\frac{p(q)}{p(0)}-1=\frac{q}{a-q}.\]
- liquidity provider makes asset and cash deposit
- more deposits flatten price curve
- may attract more volume
- but larger "positional" dollar loss when prices move
- larger liquidity deposits \(a\) \(\Rightarrow\)
- lower costs (price impact) for liquidity demanders
UniSwap v3
UniSwap v3 has "concentrated liquidity provision"
- liquidity provision choice in v2:
- submit \(a,c\) at the marginal \(p_0=\frac{c}{a}\)
- \(\to\) for given \(p_0\), there is ONE degree of freedom
- provide liquidity
- for all prices \(p\in(0,\infty)\)
- all asset amounts \(q\in(0,a)\)
- all cash amounts \(\Delta c\in (0,c)\)
- liquidity provision choice in v3:
- submit \(u,\Delta c (d)\)
- choose price range \([p_d,p_u]\)
- provide liquidity
- for all prices \(p\in[p_d,p_u]\)
- all asset amounts \(q\in(0,u)\)
- all cash amounts \(\Delta c\in (0,\Delta c(d))\)
Just a little more institutional details
-
users submit liquidity positions \((u,d,p_u,p_d)\) and receive an ERC-721 (=NFT) token as a receipt
-
the code segments liquidity into discrete exponential intervals \([p_k,p_{k+1}]\) with \[p_k=(1+\delta)^k. ~~~(\text{numerically: }p(k)=1.0001^k)\]
-
it aggregates liquidity over these intervals
-
the pricing curve for each interval is determined by the constant product rule
-
intervals may be "empty"
How the price is determined
- if the marginal price reaches the upper bound \(p_u\), you will sell \(u\) units of the asset
- if the marginal price reaches the lower bound \(p_d\), you will sell \(d\) units of the cash
- the price is still using constant product
- virtual liquidity = v2 liquidity that would pertain if you'd supply liquidity on the entire interval of prices
- constant product \(\Rightarrow\) marginal price curve has functional form \[p^m(q)=\frac{\tilde{a}c}{(\tilde{a}-c)^2}\]
where \(\tilde{a}\) is the virtual liquidity
quick disclaimer: what follows is not how UniSwap is explained on its website etc. But the resulting maths are the same
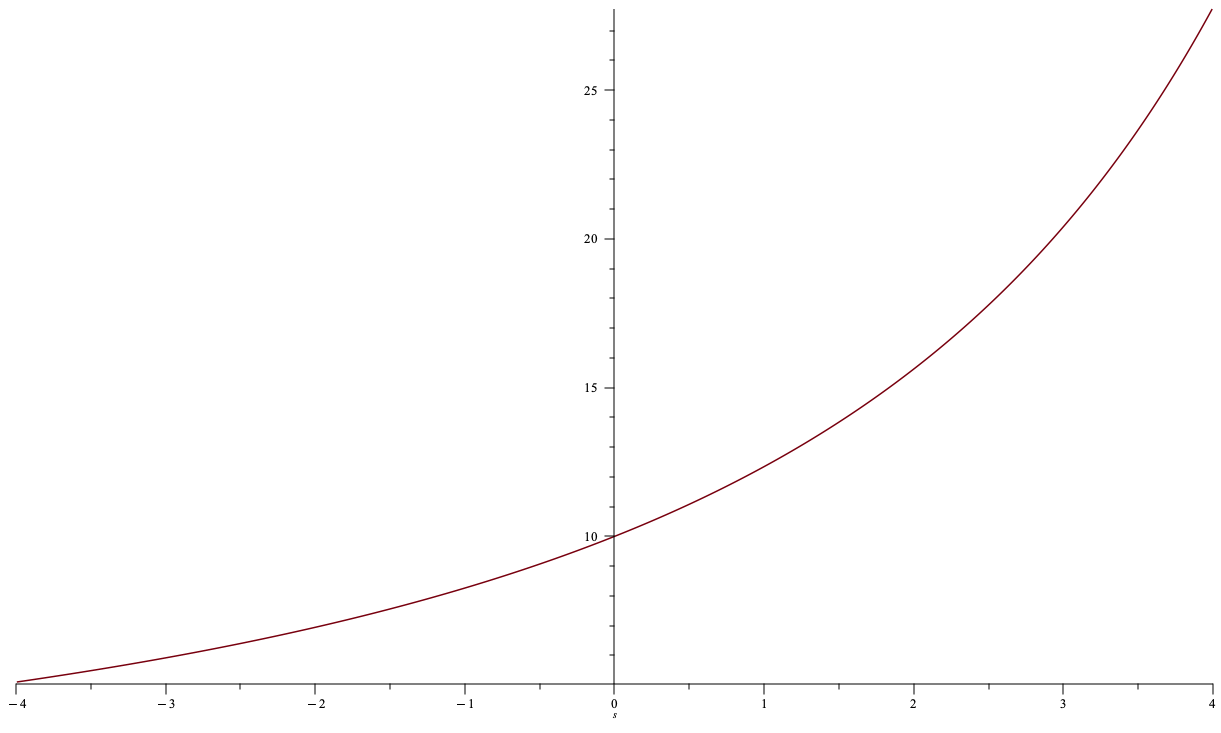
\(p_d\)
\(p_u\)
\(p_0\)
UniSwap v3: An Example
\(p_u=15\)
\(p_d=7\)
\(u=2\)

\(p_0=10\) (that's exogenous, not a choice)
marginal price
\[\gamma(s)=\frac{\tilde{a}c}{(\tilde{a}-s)^2}.\]
Finding virtual liquidity factor \(\tilde{a}\)
marginal price
\[\gamma(s)=\frac{\tilde{a}c}{(\tilde{a}-s)^2}.\]
\(p_u=15\)
\(p_d=7\)
\(u=2\)

\(p_0=10\) (that's exogenous, not a choice)
= find the right curve
= find the right "\(\tilde{a}\)"
= find \(\tilde{a}\) such that \[\gamma(u)=p_u\]
Finding the fourth parameter \(\Delta c(d)\)
\(p_u=15\)
\(p_d=7\)
\(u=2\)
\(d=?\)
required cash deposit \(\Delta c(d)=\) the amount that I pay for \(d\)
marginal price
\[\gamma(s)=\frac{\tilde{a}c}{(\tilde{a}-s)^2}.\]
Given \(\tilde{a}\) solves \(\gamma(u)=p_u\), we
- solve \(\gamma(d|\tilde{a})=p_d\) for \(d\)
- determine \(\Delta c(d|\tilde{a})=\) the required cash
Solutions
- virtual liquidity factor: \[\tilde{a}=\frac{u}{1-\sqrt{p_0/p_u}}=u\cdot \frac{\sqrt{p_u}}{\sqrt{p_u}-\sqrt{p_0}}.\]
- required quantity to reach \(p_d\) \[\rho(-\tilde{d})=\frac{\tilde{a}\tilde{c}}{(\tilde{a}+\tilde{d})^2}=p_d.~~\Leftrightarrow~~d^*=-\tilde{a}(1-\sqrt{p_0/p_d})\]
- required cash deposit \[\Delta c(\tilde{d})=-\tilde{a}(1 - \sqrt{p_0/p_d})\sqrt{p_0p_d}=-u\sqrt{p_0p_d}\frac{1 - \sqrt{p_0/p_d}}{1 - \sqrt{p_0/p_u}}\]
- marginal pricing function \[\tilde{\gamma}(q)=\frac{\tilde{a}^2p_0}{(\tilde{a}-q)^2}=\frac{u^2p_0p_u}{((u-q)\sqrt{p_u}+q\sqrt{p_0})^2}.\]
For those in the know: These formulae/solutions are exactly the same as those in the UniSwap v3 whitepaper
Numerical example
- Suppose \(p_0=\$10\).
- LP is willing to sell up to \(u=100\)
- v2 liquidity:
- Required cash deposit: \(c=100\times 10=1000\)
- liquidity \(c\cdot a=100\times 1,000\)
- For v3: suppose willing to supply liquidity in \([\$9,\$11]\)
- v3 liquidity:
- virtual liquidity factor: \(\tilde{a}\approx 2,150\)
- required cash \(c^*=\$1,100\)
- consider a buy order of \(q=10\)
- cost per unit
- v2: \(\frac{1000}{100-10}=11.11\)
- v3: \(\frac{21,500}{2,150-10}=10.05\)
Want to read more?
- A Primer on UniSwap v3 Math: As Easy as 1,2, v3 https://blog.uniswap.org/uniswap-v3-math-primer
- Elts 2012: Liquidity Math in UniSwap v3
- Hasbrouck, Riviera, Saleh (2023):
- UniSwap Liquidity Provision is like a covered call,
- whereas a standard market (Copeland & Galai JF 1983) is a short strangle (call at the ask, put at the bid)
Liquidity Supply and Demand in an Automated Market Maker
Facts about modelling liquidity provision
- You provide liquidity when the marginal price at the AMM and elsewhere is \(p(t_0)=p.\)
- You make a decision what to do next at \(t_1>t_0\)
- Many things can happen, for instance:
- There was no trade on the AMM but the price on another market has moved.
- There have been trades on the AMM but the AMM price is different from prices elsewhere.
- There have been trades on the AMM and the AMM price is that same as prices elsewhere.
Each case has a different interpretation and each has been used in some form in the literature.
Key questions:
- Is there arbitrage?
- Is one of the prices "correct"?
- What has happened between \(t_0\) and \(t_1\)?
Two broad approaches for modelling liquidity provision
-
Provide-and-Forget Liquidity provision
- Check-in times are far apart, \(t_1\gg t_0\)
- Price at \(t_1\) is efficient/the truth
- There was a price-moving trade and lots of other trades
- \(\to\) liquidate position at fair price
-
Liquidity Provision using options-like thinking
- Check-in time close to original time \(t_1=t_0+dt\)
- Price at \(t_1\) may be right or wrong
- Usually just a single trade
- \(\to\) may be able to rebalance position cheaply at another price
- hedge risk like an options market maker
You worry about the positional loss relative to any income.
You worry whether you can rebalance your liquidity profitably.
(im)permanent loss
"LVR" = loss-vs-rebalancing
- Aoyagi and Ito (2021), Cartea, Drissi, Monga (2023), Milionis, Moallemi, Roughgarden, and Zhang (2022), Milionis, Moallemi, Roughgarden (2024)
- Lehar and Parlour (2021), Hasbrouck, Riviera, Saleh (2023), Park (2021), Malinova and Park (2023)
Provide-and-Forget Liquidity Provision (HODL)
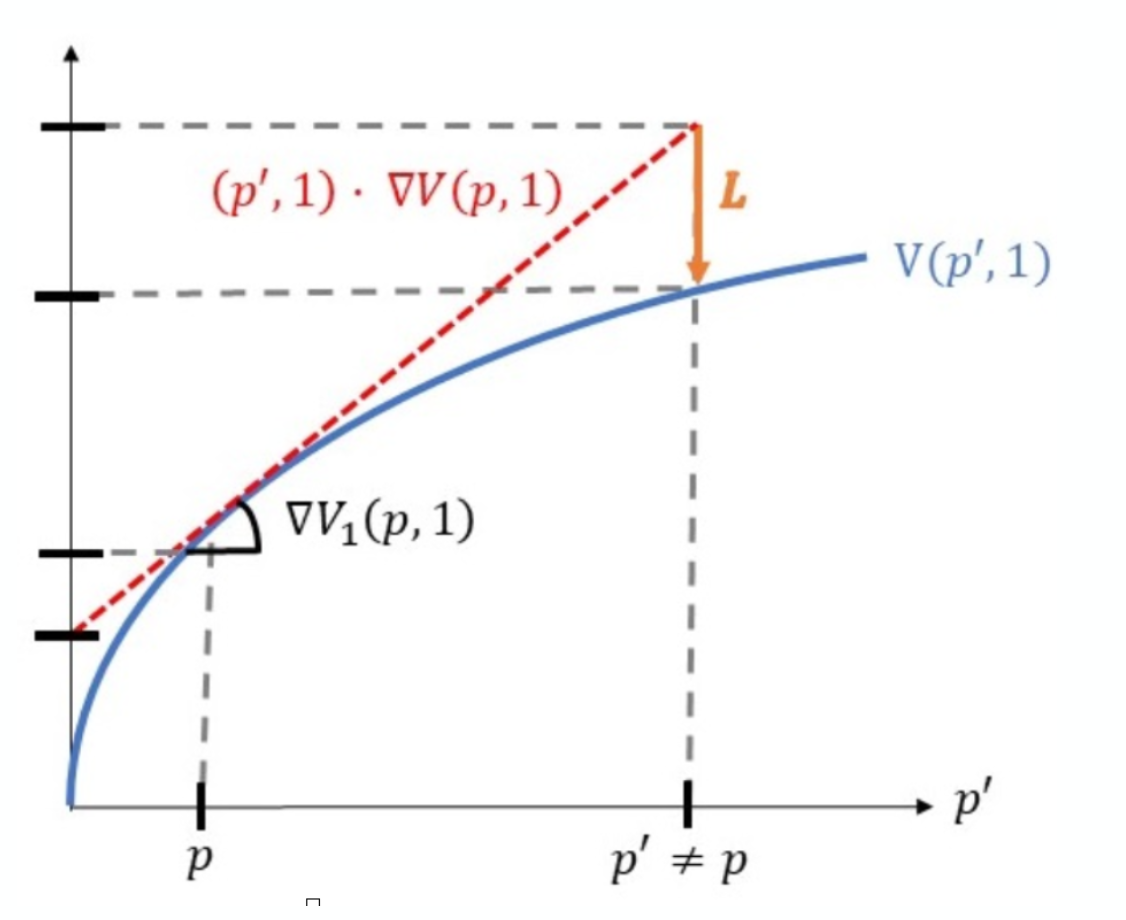
- Deposit asset & cash when the asset price is \(p\)
- Withdraw at price \(p'\ne p\)
Buy and hold
Provided liquidity
in the pool
- Why?
- adverse selection losses
- arbitrageurs trade to rebalance the pool
- \(\to\) always positional loss relative to a "buy-and-hold"
Provide-and-Forget Liquidity Provision
\[\underbrace{F \int DV \mu(DV) }_{\text{fees earned on}\atop \text{balanced flow}}+\int_0^\infty\underbrace{(\Delta c(q^*)-q^*p_t(R)}_{\text{adverse selection loss} \atop \text{when the return is {\it R}}} +\underbrace{F \cdot \Delta c(q^*))}_{\text{fees earned}\atop \text{from arbitrageurs}}~\phi(R)dR \ge 0.\]
\(q^* \) is what arbitrageurs trade to move the price to reflect \(R\)
Basic idea of liquidity provision: earn more on balanced flow than what you lose on price movement
\[\text{fee income} +\underbrace{\text{what I sold it for}-\text{value of net position}}_{\text{adverse selection loss}} \ge \text{cost of capital} \]
in AMMs:
protocol fee
in tradFi: bid-ask spread
- Malinova & Park (2023): express equation with returns
- single variable decision problem as fraction of shares outstanding
- allows calibration to any market
- With constant product AMM (includes v3), when the fundamental moves, there is always a positional loss.
- With COW Swap pricing, when the fundamental moves, there is never a positional loss.
Sidebar: we can quantify how much a PASSIVE LP loses when the price moves by \(R\)
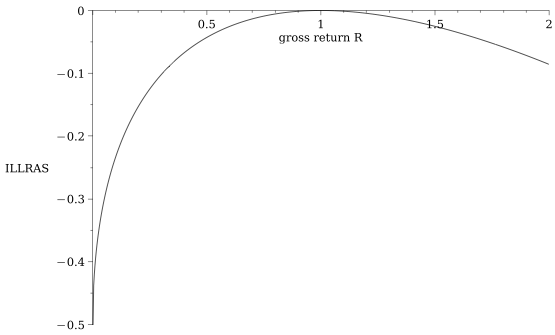
for orientation:
- If the stock price drops by 10% the incremental loss for liquidity providers is 13 basis points on their deposit
- \(\to\) total loss=-10.13%
- If the stock price rises by 10%, the liquidity provider gains 12 basis points less on the deposit
- \(\to\) total gain =9.88%
\[\frac{\text{adverse selection loss when the return is \(R\)}}{\text{initial deposit}}=\sqrt{R}-\frac{1}{2}(R+1)\]
see Barbon & Ranaldo (2022)
adverse selection loss
(or: impermanent loss)
Liquidity Demander's Decision & (optimal) AMM Fees
- Two opposing forces in equilibrium for fee \(F\nearrow\)
- more liquidity provision
\(\to\) lower price impact - more fees to pay
- more liquidity provision
Result:
competitive liq provision\(\to\) there exists an optimal (min trading costs) fee \(>0\)
- \(\to\) derive closed form solution for competitive liquidity provision
- depends on return distribution, balanced volume, quantity demanded
Similar to Lehar&Parlour (2023) and Hasbrouck, Riviera, Saleh (2023)
- For trading of a fixed quantity:
\[\text{LD cost}=\text{AMM price impact} +\text{AMM fee} .\]
\[F^\pi=\frac{1}{E[|\sqrt{R}-1|/2]+V}\left(-2q\ E[\text{position loss}]+ \sqrt{-2qV\ E[\text{position loss}]}\right).\]
assume: liquidity providers add liquidity until they break even in expectation
Liquidity Provision as Options
- Liquidity = give others the option to trade
- Limit order book: (Copeland & Galai JF 1983) liquidity provision \(=\) is a short strangle: call at the ask, put at the bid
- Hasbrouck, Riviera, Saleh (2024): AMM v3 Liquidity Provision is a covered call
- long in the underlying (when price drops, they hold the asset)
- sell a call (when the price rises, their payoff is as if writng a call)
- earn fees (premium) when the price is below the strike
-
Milionis, Moallemi, Roughgarden, and Zhang (2022): A LVR strategy has several analogies in options pricing
- it's a bit like a protective put: rebalancing protects against losses
- it's a bit like Delta-Hedging to stay neutral to price movements
Ciamac Moallemi will explain details later!
Loss-vs-Rebalancing
- Idea:
- price moves in broader market
- can rebalance at external price - sometimes at a profit
- Example: in UniSwap v2, your position in the risk asset as a function of its broader price \(P\) for starting liquidity \(L\) should be \(a(P)=L/\sqrt{P}\)
- Value of the rebalancing portfolio is initial value \(+\) weighted sum of all rebalancing actions
- Loss-vs-rebalancing \(=\) rebalanced portfolio value \(-\) un-rebalanced portfolio
- Theorem (Milionis, Moallemi, Roughgarden, Zhang 2022): non-negative, no decreasing, deterministic function with explicit functional form.
Loss-vs-Rebalancing
\[\text{Liquidity position P\&L}=\text{fee income} +\text{pool value after at \(t\)} -\text{pool value at \(0\)}\]
\[=\text{rebalanced value at \(t\)} -\text{pool value at \(0\)} +\text{fee income}-\text{LVR}.\]
\[=\underbrace{\text{rebalanced value at \(t\)} -\text{pool value at \(0\)}}_{\text{is hedge-able (Delta-hedge type strategy)}} +\text{fee income}-\text{LVR}.\]
- How is this useful? \(\to\) compute the P&L of liquidity provision!
\[\text{{\it hedged} Liquidity position P\&L}=\text{fee income}-\text{LVR}.\]
Ciamac Moallemi will later explain how hedging then improves the Sharpe Ratio substantially!
LVR vs IPL
\[\text{{\it hedged} Liquidity position P\&L}=\text{fee income}-\text{LVR}.\]
What's the difference of LVR to ImPermanent Loss?
- ex ante they are the same
- but LVR allows "profitable" rebalancing (arbitrage against yourself)
- IPL assumes someone else does arbitrage \(\to\) creates fees
\(\Rightarrow\) different perspective of market making
\[\text{{\it unhedged} HODL Liquidity Position P\&L}=\text{fee income}-\text{IPL}.\]
Empirical Work
Lehar and Parlour (2021)

Barbon & Ranaldo (2023)
Other notables:
- Lehar, Parlour, Zoican (2022):
- study and document fragmentation of liquidity across different fee levels
- most intense provision-withdrawal activity for low fees \(\to\) UniSwap v3 starts mimicking tradfi
- Capponi & Jia (2022) study impact of curvature of pricing function
- Theory: curvature of optimal pricing curve \(\nearrow\) volatility
- Empirics: cost volatility is 60% lower for stable-coin pairs
- corr(deposit inflows ,volatility)<0
corr(deposit inflows ,volume)>0
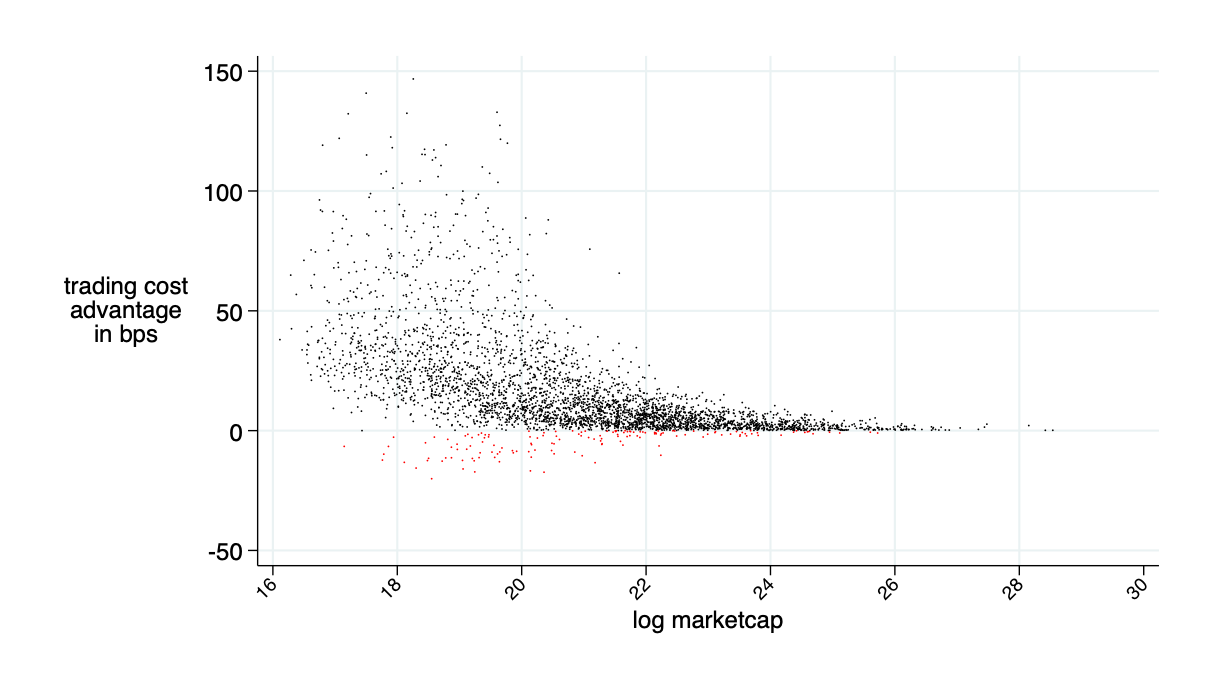
Malinova & Park (2023): AMM applied to equities would reduce trading costs by 30%
Concerns around Automated Market Makers







































a
b
c
d
e
f
g






Problem 1: Sandwich (MEV) attacks
related paper: “Maximal Extractable Value and Allocative Inefficiencies in Public Blockchains”. A. Capponi, R. Jia, and Y. Wang (2023)
- With v2 AMM pricing, losses are arbitrarily large (Park 2023)
- Slippage protection can mitigate losses but comes with execution risk
NB: PBS does not solve the problem

























a
b
c
d
e
f
g






Problem 2: Arbitrage Trades that Reduce LVR
- Key LVR Idea:
- rebalancing benefits liquidity providers
- allows lower equilibrium fees
PBS creates the problem
builder/searcher
- Arbitrage
- reduces rebalancing benefits
- \(\to\) eliminates the fee advantage
- \(\to\) increases equilibrium fees
Problem 3a: Just-In-Time Liquidity (single trade cream skimming)
X-Router


Liquidity pool
OTC
Problem 3b: Just-In-Time Liquidity (at the builder/MEV level)
X-Router


Liquidity pool
searcher/builder
balanced orders
add as much liquidity as possible
withdraw liquidity
unbalanced orders
- the issue:
- order flow segmentation increases adverse selection
- JIT: not enough fees from balanced order flow
related paper: Capponi, Jia, and Zhu (2024) "The Paradox of Just-in-Time Liquidity in Decentralized Exchanges: More Providers Can Lead to Less Liquidity"
The Bigger Picture and Last Words
Last Words
- AMMs are a genuinely new market institution
- evolving space, new ideas come up all the time:
- UniSwap v4 is here - can it solve the problems?
- may be embedded in many applications and processes
- lots to learn
- Will we re-discover and re-create many of the problems of existing markets?
@financeUTM
andreas.park@rotman.utoronto.ca

slides.com/ap248
sites.google.com/site/parkandreas/
youtube.com/user/andreaspark2812/
From Vitalik Buterin's post on the topic:
https://ethresear.ch/t/improving-front-running-resistance-of-x-y-k-market-makers/1281
- February 2022: UniSwap (V2), ETH-USDC
- 38,100 ETH
- 118M USDC
- \(p=\$3,097\)
- Buy: 100 ETH
- pay approximately $3,105 per ETH. accoridng to bonding curve
- 100 ETH MEV sandwich attack
- Initial trade cost: $3,105 per ETH
- reversing yields $3,121 per ETH
- total profit of $1,639 \(=\) value extracted from original trader.
- 1,000 ETH MEV attack
- profit/loss \(=\) $17K
- 10,000 ETH MEV attack
- profit/loss \(=\) $261K.
Theorem (Park 2023):
- Constant product pricing and linear limit order book pricing allows unlimited MEV losses
- Uniform pricing has limited MEV losses but profitable splitting
Hypothetical example
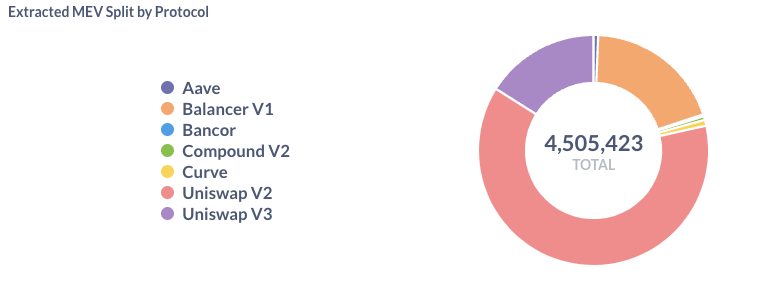
The Bigger Picture: MEV Extraction

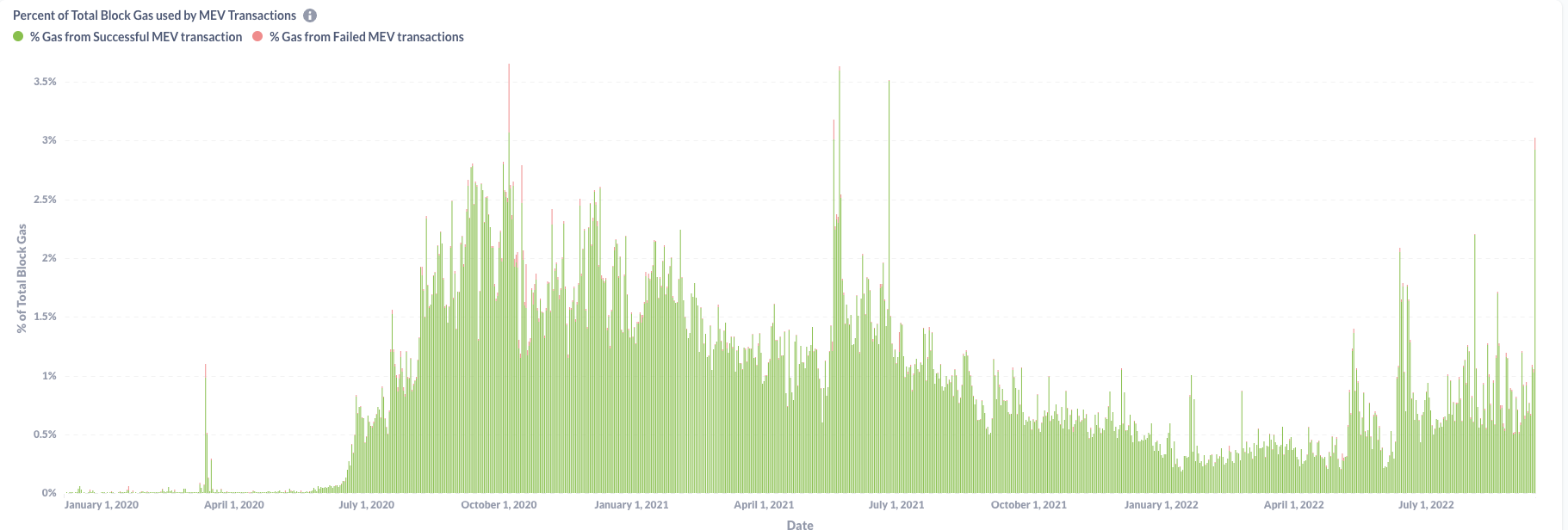
- MEV extraction is a reality and almost inevitable
- imposes negative externalities as e=bots bid up gas prices
- "Flashbots" protocol "democratizes" exploits
- protocols became better at preventing sandwich attacks with better functionality
read more at: "Battle of the Bots: Flash Loans, Miner Extractable Value and Efficient Settlement", Lehar & Parlour, 2023

| limit order book | periodic auctions | AMM | |
|---|---|---|---|
| continuous trading |
|||
| price discovery with orders | |||
| risk sharing |
|||
| passive liquidity provision | |||
| price continuity |
|||
| continuous liquidity | |||
| sniping prevented |










Two views
- You may trade with uninformed or informed.
- you may have a position gain (against uninformed) or loss (against informed)
- example: Aoyagi and Ito (2021) "Coexisting Exchange Platforms: Limit Order Books and Automated Market Makers", Cartea, Drissi, Monga (2023)
- You trade over time with informed and uninformed
- you always lose but get compensated over time
- examples: Lehar and Parlour (2021), Hasbrouck, Riviera, Saleh (2023), Park (2021), Malinova and Park (2023)
- Lehar and Parlour (2021) assume that every uninformed trade is off-set by an arbitrageur \(\to\) more fee income
- between deposit and withdrawal, asset value changes from \(V_0\to V_t\) and price \(p_0\to p_t\)
- efficient pricing: \(p_t=V_t\)
- gross return \(R=p_t/p_0\)
- in AMM, only trades move price
- between deposit and withdrawal, trade with informed and uninformed
Two views
- You may trade with uninformed or informed.
- you may have a position gain (against uninformed) or loss (against informed)
- example: Aoyagi and Ito (2021) "Coexisting Exchange Platforms: Limit Order Books and Automated Market Makers", Cartea, Drissi, Monga (2023)
- You trade over time with informed and uninformed
- you always lose but get compensated over time
- examples: Lehar and Parlour (2021), Hasbrouck, Riviera, Saleh (2023), Park (2021), Malinova and Park (2023)
- Lehar and Parlour (2021) assume that every uninformed trade is off-set by an arbitrageur \(\to\) more fee income
- between deposit and withdrawal, asset value changes from \(V_0\to V_t\) and price \(p_0\to p_t\)
- efficient pricing: \(p_t=V_t\)
- gross return \(R=p_t/p_0\)
- in AMM, only trades move price
- between deposit and withdrawal, trade with informed and uninformed
How the price is determined
- In v2, for given \(p_0=\frac{c}{a}\), users have ONE degree of freedom.
- for instance, when you pick prices \(p_u,p_d\) and the quantity \(u\) that you are willing to supply, then the amount of cash that you have to contribute is pre-determined.
- You can pick \(p_d=p_0\) so that \(\Delta c(d)=0\)
- In v3, for given \(p_0\), users have THREE degree of freedom.
Theory Literature on AMM
- Lehar & Parlour (JF 2024): compares LOB with CP for theory and empirics
- Barbon & Ranaldo (2022): empirics on trading costs; closed form solution to loss
- Milionis, Moallemi, Roughgarden, and Zhang (2022) have dynamic analysis of impermanent loss (or, rather, "loss vs rebalancing" (LVR))
- Hasbrouck, Riviera, Saleh (2023): optimal trading fee \(\not=\) 0
- Park (2023): analysis of price functions properties
- Malinova & Park (2023): calibrate AMM to equity markets
Traditional Markets
What is Market Microstructure?
- How do trading institutions affect market outcomes, e.g.
- trading costs
- information efficiency
- allocative efficiency
- A lot of tricky issues
- no one model can do it all
- complex theoretical problems (e.g., infinite regress)
- large datasets


Broker


Exchange
Internalizer
Wholeseller
Darkpool


Venue



Settlement
Traditional Institutions
Investors
Trading Arrangements
central limit order book
complexity
price impact of trades
anonymity
price discovery
centralized auction
bilateral
negotiation
Request
for Quote
open
outcry
Who trades?
- Most of the time there is no "coincidence of wants"
- \(\Rightarrow\) Need intermediating liquidity providers!
- What's there first?
- trader's order \(\equiv\) liquidity provision
- trader's order \(\to\) liquidity provision
- liquidity provision \(\to\) trader's orders
- Deeply affects models and modelling choices
Key question for liquidity provision
- Why is there trading?
- diversification/liquidity shocks
- private information
- arbitrage
Seminal papers
- trader's order \(\equiv\) liquidity provision
- trader's order \(\to\) liquidity provision
- liquidity provision \(\to\) trader's orders
What's there first? Orders or Liquidity?
Seminal papers
- trader's order \(\equiv\) liquidity provision
- Grossman & Stiglitz (AER 1980)
- trader's order \(\to\) liquidity provision
- Kyle (ECTA 1985)
- Grossman & Miller (JF 1988)
- liquidity provision \(\to\) trader's orders
- Glosten & Milgrom (JFE 1986)
- Foucault (JFM 1999)
- people "buy" noisy information
- demand = supply
- price reveals information
- marginal value of info = cost of info
- competitive liquidity provider receives order flow and sets zero-profit price
- noise trader order flow
- monopolist informed trader cautiously trades over time to conceal info
- slope of the price curve measures liquidity
- risk-averse market makers require compensation for risk-taking (position risk)
- liquidity-motivated traders submits order
- what determines the price slope?
- informed and uninformed arrive in random sequence at the market
- market maker posts bid and ask prices that account for info-driven loss
- what determines the spread?
- submit market vs limit order?
- post limit order = trading option for others
- fundamental may change and may not be able to adjust limit order
- gives rise to price slope and spread
Basics of liquidity provision under value uncertainty
- fundamental value up
- \(\Rightarrow\) price up
- \(\Rightarrow\) sell the asset for less than its worth
- \(\Rightarrow\) price up
- fundamental value down
- \(\Rightarrow\) price up
- \(\Rightarrow\) buy the asset for more than its worth
- \(\Rightarrow\) price up
Questions:
- What are the fees/cash sources of income?
- When does/did the value change?
- When do I assess the positional gain/loss?
- liquidity provision = accept a risk
- risk = fundamental value may change (or may have already changed and you don't know it)
every model has some form of structure like
\[\text{trading income (fees, spreads, etc)} +\underbrace{\text{what I sold it for}-\text{value of net position}}_{\text{positional gain/loss}} \ge \text{outside option} \]
Example 1: Grossman/Miller
- Any position is a risk \(\to\) cost
- always over-price the trade to compensate for risk
Example 2: Kyle or Glosten-Milgrom
- trade with informed:
- receive too little/pay too much
- trade with uninformed:
- pay too little/receive too much
- trade-by-trade view
- can either trade on "other" market
- hold asset to maturity
Example 3: Limit order market (a la Glosten 1994)
- trade with uninformed:
- overprice small orders
- trade with informed:
- underprice small orders
Crypto vs TradFi Markets
- Self-custody of assets
- Access to financial infrastructure
- Blockchain as value management layer = common resource
- Platform approach to commerce
Key Differences Defi vs TradiFi
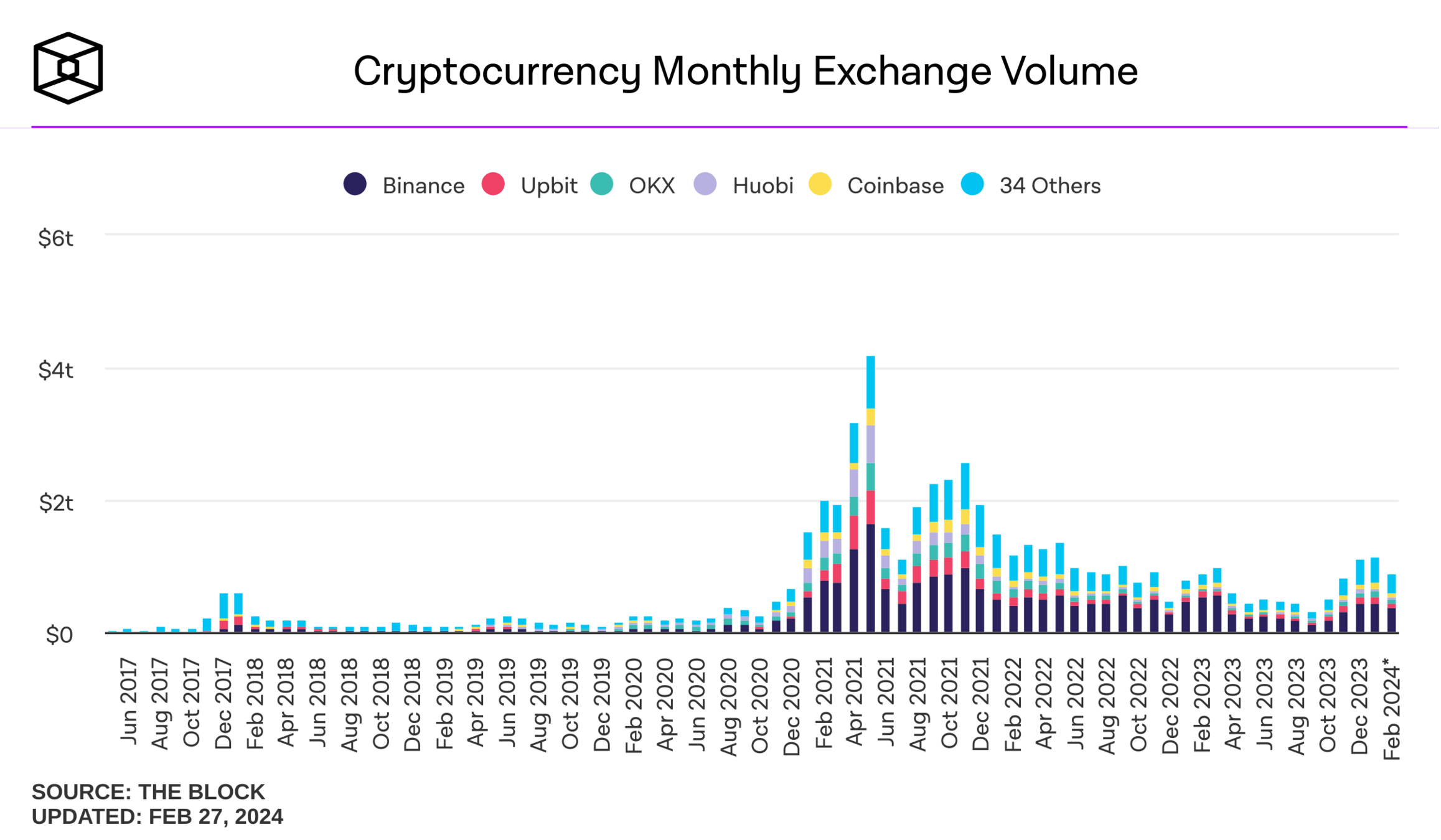
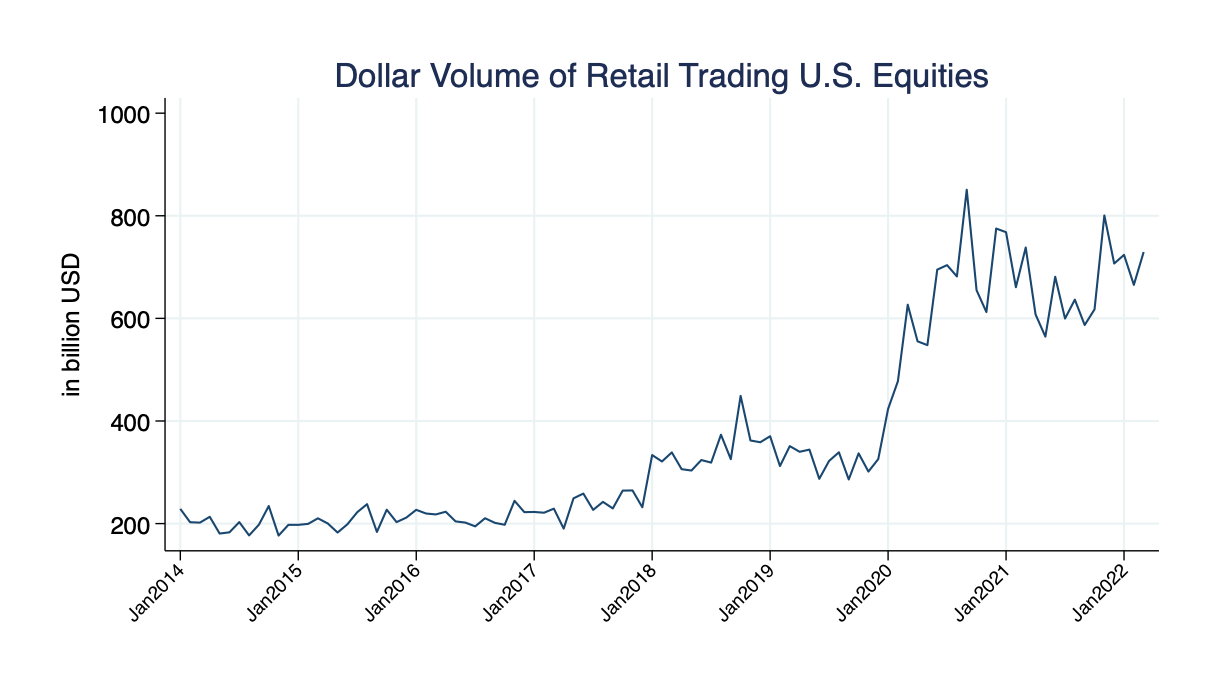
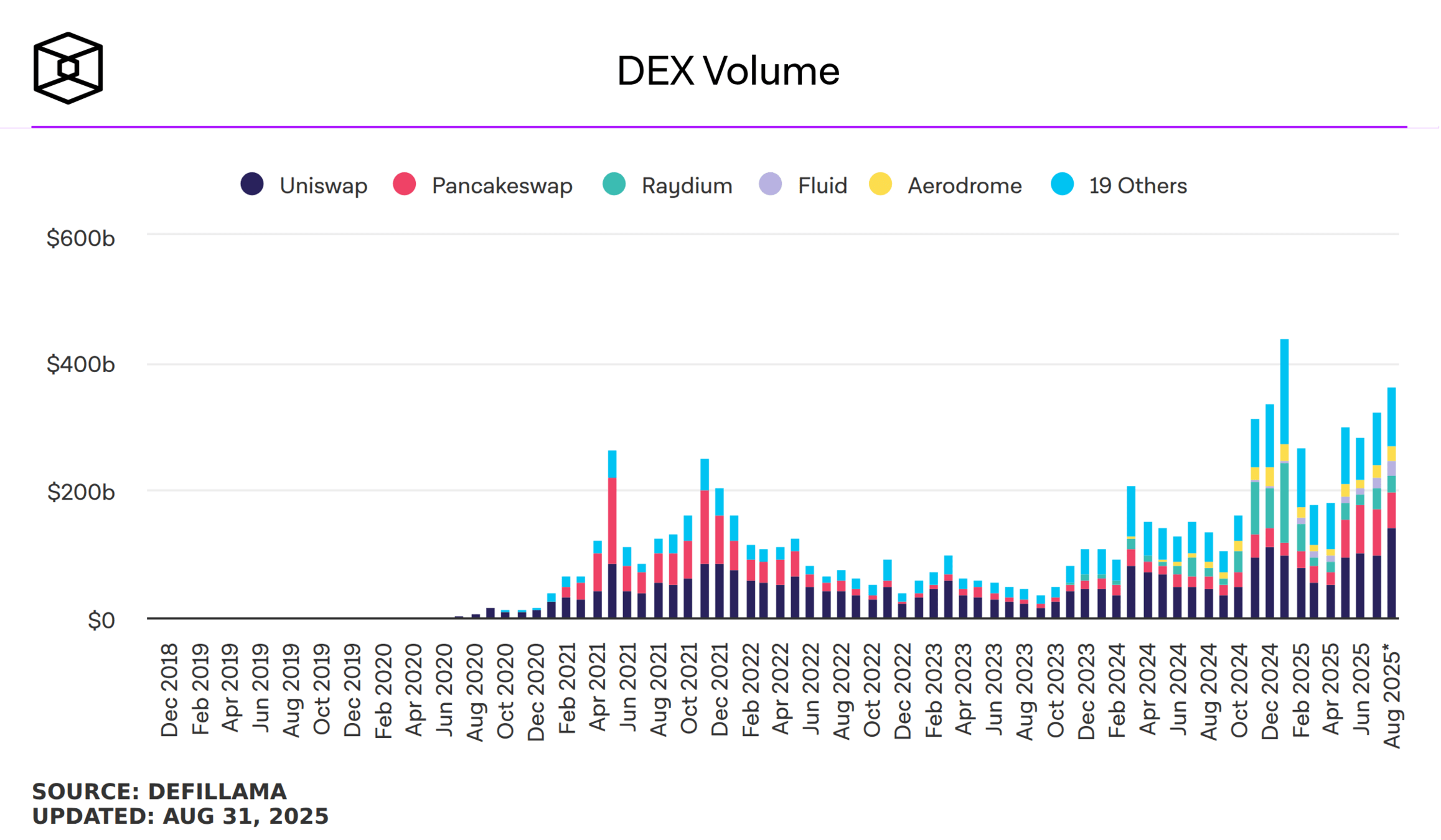
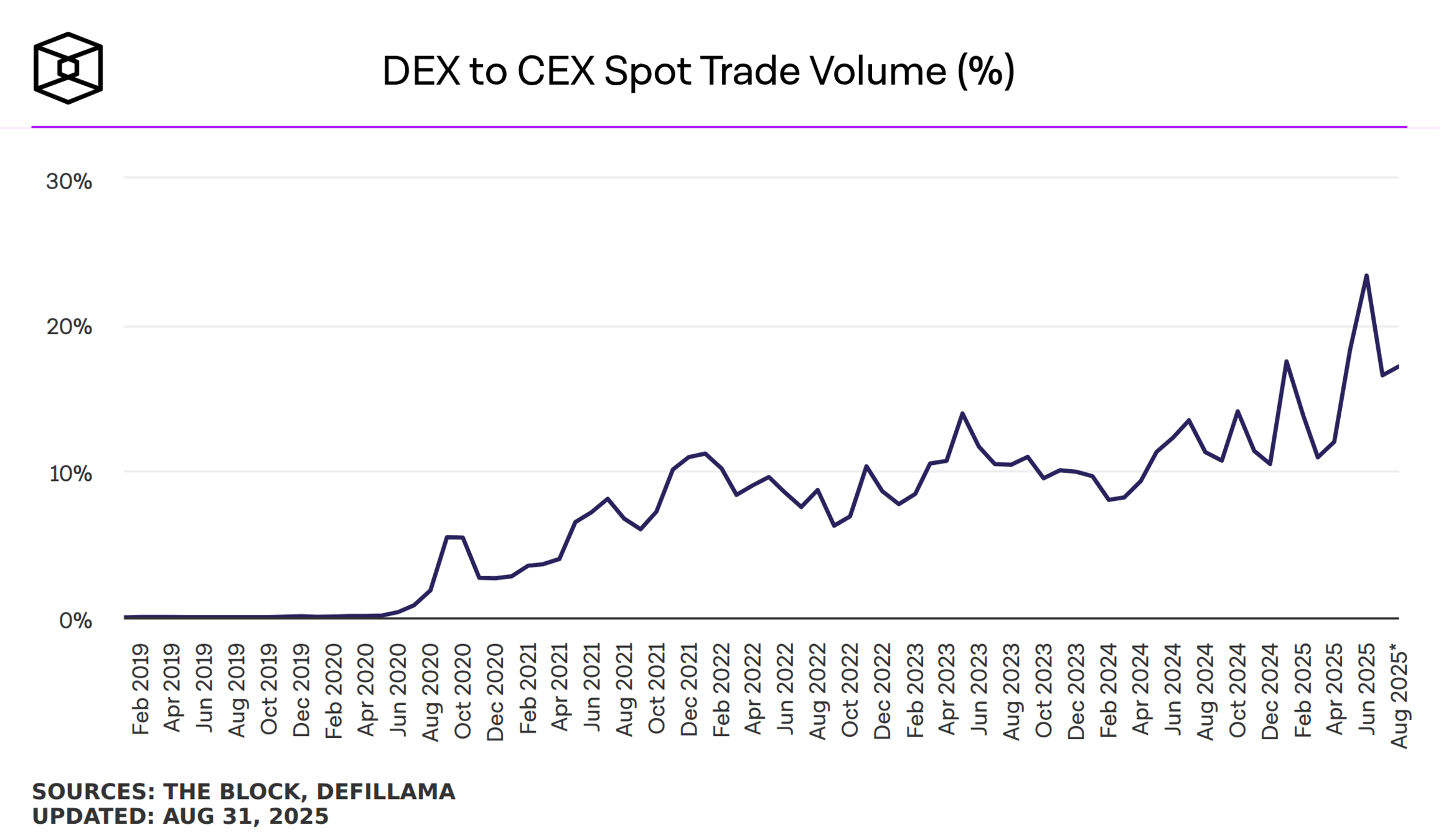
- data: authors calculations from TAQ (up to March 2023)
- crypto volume worldwide is larger than US retail by factor >4



















Broker


Exchange
Internalizer
Wholeseller
Darkpool


Venue



Settlement
Investor
Centralized Trading

















Issues and concerns with CEX trading
- No shortage of drama!
- A short list of issues
- expensive arbitrage
- price manipulation
- volume manipulation
- security risk
- Google "Lazarus Group"
- Are they unlicensed securities exchanges?
Costly Arbitrage
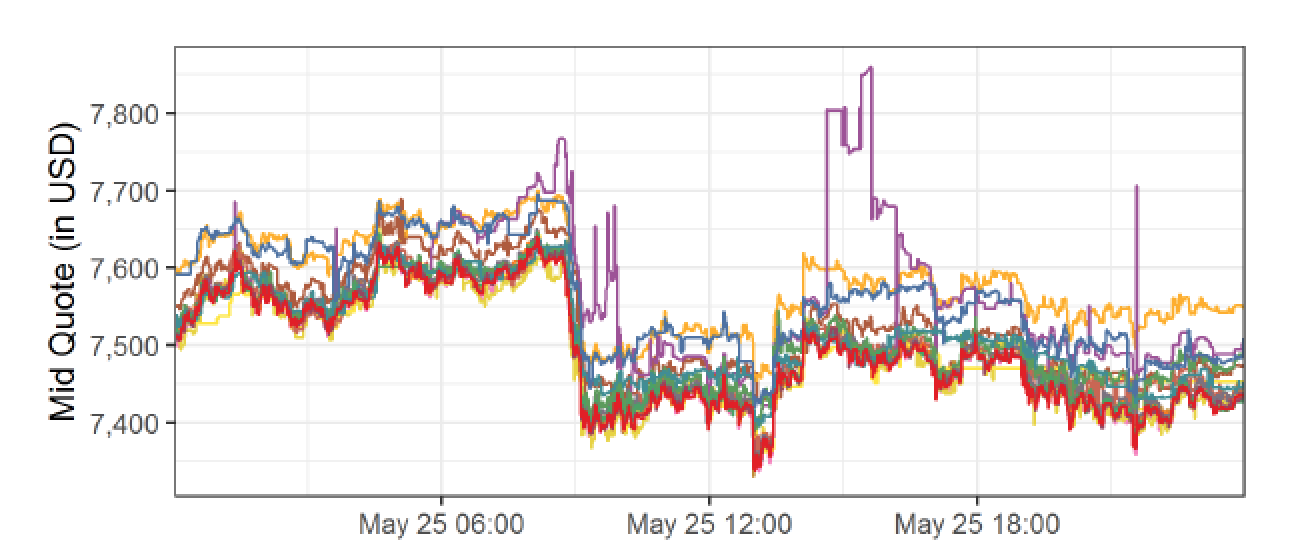

BTC/USD
ask: 7,600
bid: 7,550
BTC/USD
ask: 7,500
bid: 7,450

buy BTC
sell BTC
move BTC to Kraken



=> arbitrage = commit capital on multiple exchanges
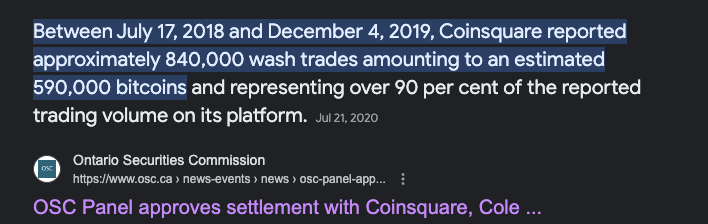
Crypto Wash Trading, Lin William Cong, Xi Li, Ke Tang, Yang Yang
- systematic tests:
- robust statistical and behavioral patterns in trading to detect fake transactions on 29 cryptocurrency exchanges.
- Regulated exchanges are OK
- unregulated exchanges: rampant manipulations
- wash trading on each unregulated exchange:
- on average over 70% of the reported volume
- improve exchange ranking
- temporarily distort prices
Volume Manipulation
Cryptocurrency Pump-and-Dump Schemes
Tao Li, Donghwa Shin, and Baolian Wang, 2020

What is pump and dump?
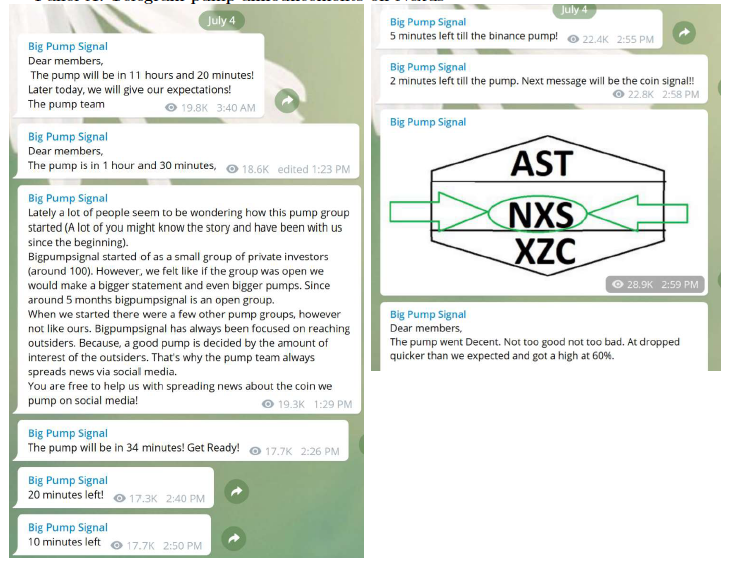
arranged via Telegram Channels
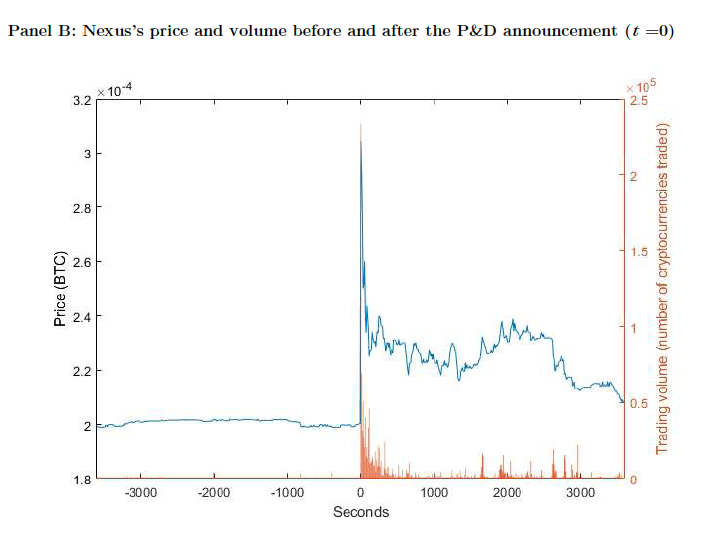
Price Manipulation: Pump & Dump



August 2016




Security Risk

















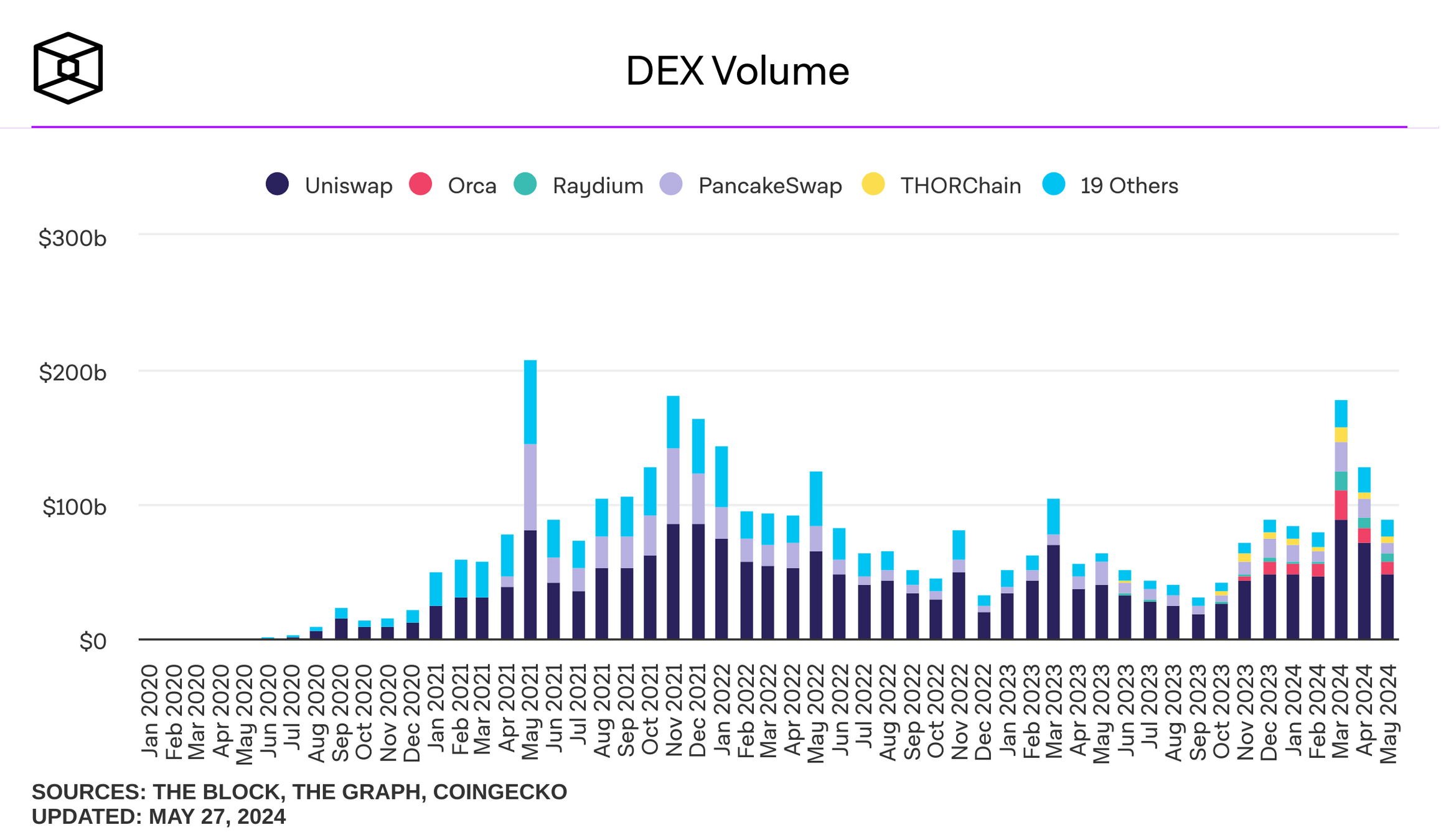
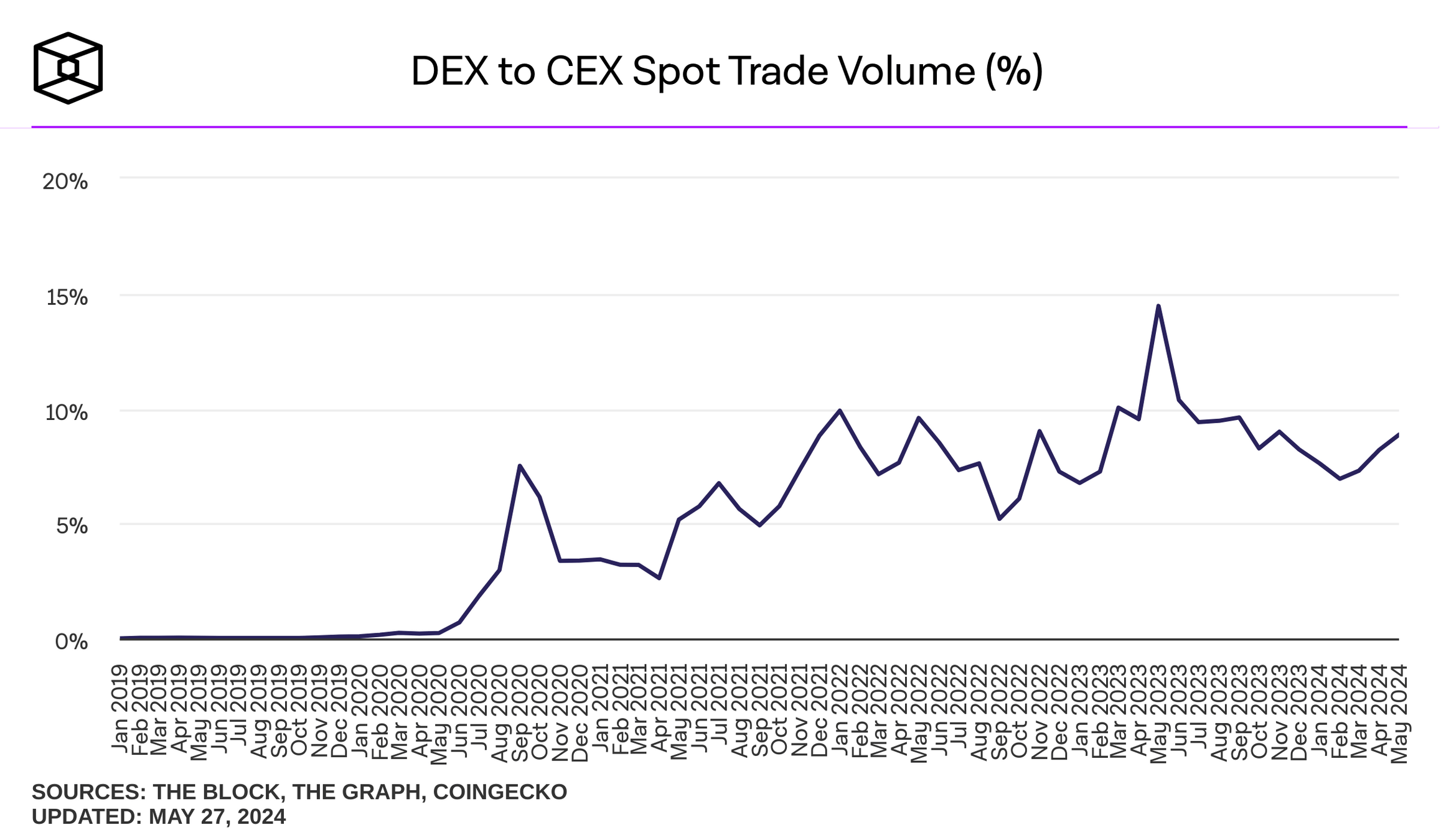
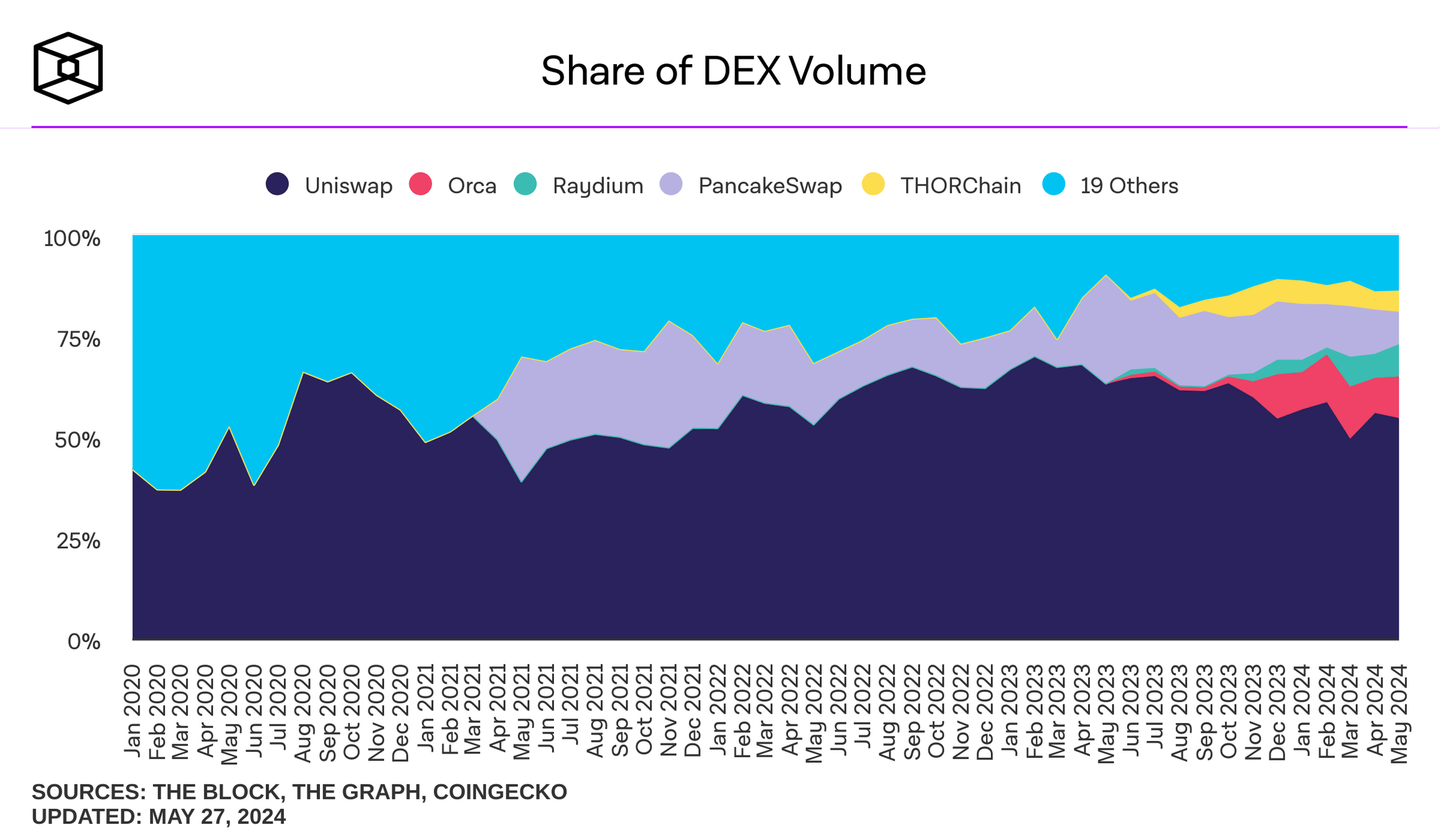
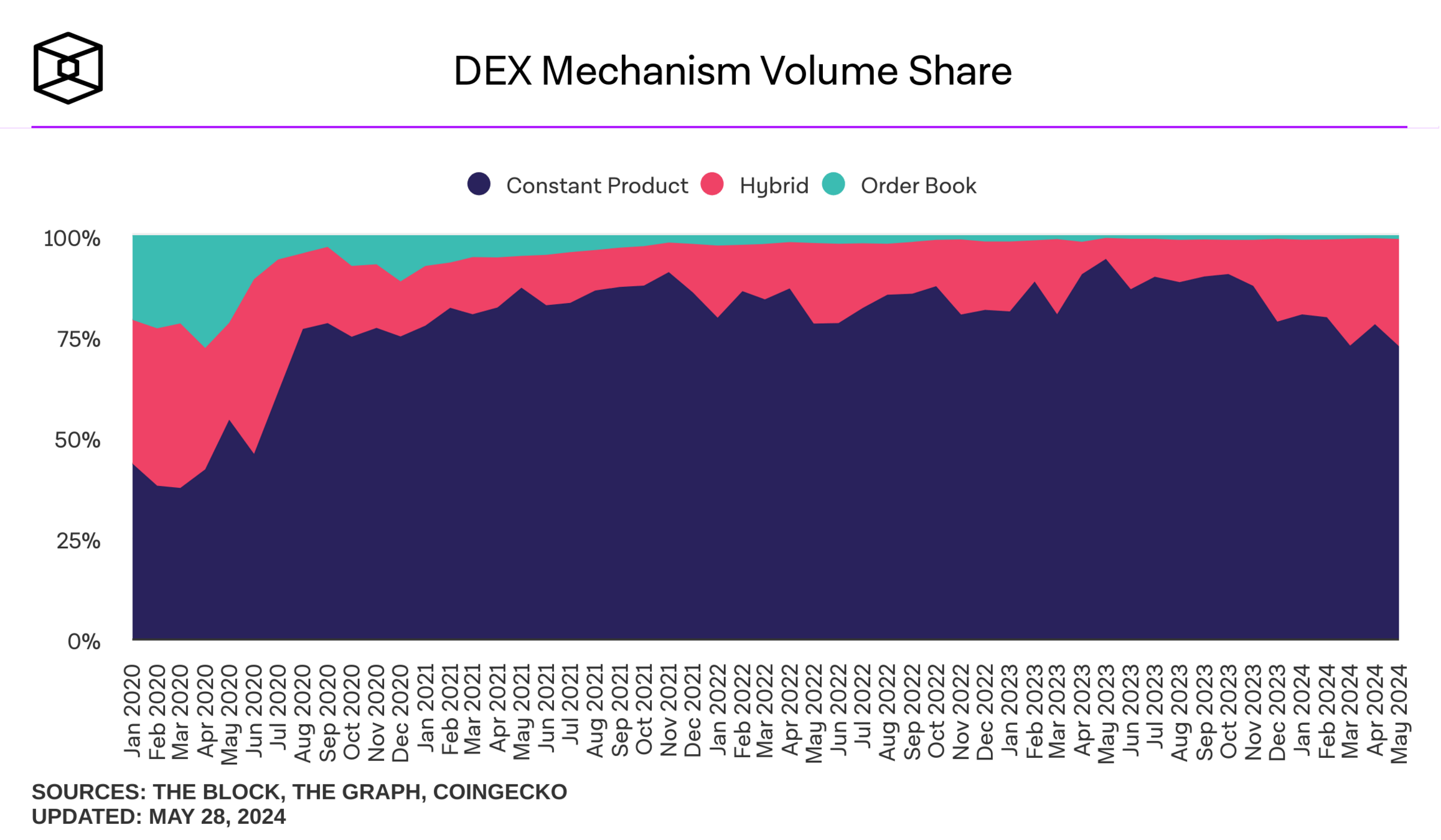
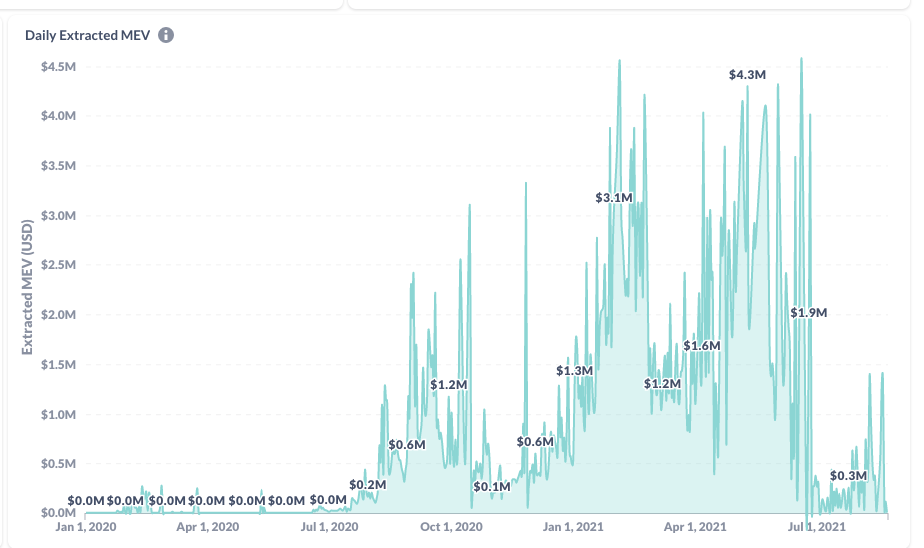
where do I find these plots? theblock.co/data/


... 300 lines of code ...

Can we run a limit order book directly on the blockchain? Yes, but ...
- for reference: NASDAQ creates several peta-bytes worth of data each month!
- \(\to\) on-chain order book is a really bad idea!
- \(\to\) Data-intensive, computation intensive, costly, inefficient

















How do people trade on-chain?
Literature
AMM Literature: a booming field
- Theory
-
Lehar and Parlour (2021): for many parametric configurations, investors prefer AMMs over the limit order market.
-
Aoyagi and Ito (2021): co-existence of a centralized exchange and an automated market maker; informed traders react non-monotonically to changes in the risky asset’s volatility
-
Capponi and Jia (2021): price volatility \(\to\) welfare of AMM LPs; conditions for a breakdown of liquidity supply in the automated system; more convex pricing \(\to\) lower arbitrage rents & less trading.
-
Capponi, Jia, and Wang (2022): decision problems of validators, traders, and MEV bots under the Flashbots protocol.
-
Park (2021): properties and conceptual challenges for AMM pricing functions
-
Milionis, Moallemi, Roughgarden, and Zhang (2022): dynamic impermanent loss analysis for under constant product pricing.
-
Hasbrouck, Rivera, and Saleh (2022): higher fee \(\Rightarrow\) higher volume
-
-
Empirics:
-
Lehar and Parlour (2021): price discovery better on AMMs
-
Barbon and Ranaldo (2022): compare the liquidity CEX and DEX; argue that DEX prices are less efficient.
-
-
Math Literature: large number of papers that study AMMs in applied maths
- e.g. Cartea, Drissi, Monga (2023): closed form solution to IPL and optimizing strategy
Trading Infrastructure
payments network
Stock Exchange
Clearing House
custodian
custodian
beneficial ownership record
seller
buyer
Broker
Broker
IS BITCOIN REALLY UN-TETHERED? JOHN M. GRIFFIN and AMIN SHAMS
Journal of Finance 2020
- Tether = ‘pushed’
- print an unbacked digital dollar to purchase Bitcoin.
- \(\to\) additional supply of Tether creates unwarranted inflation in Bitcoin price


vs.
- Tether = ‘pulled’
- driven by legitimate demand from investors who use Tether as a medium of exchange
- \(\to\) the price impact of Tether reflects natural market demand
Price Manipulation: Pumping Bitcoin
Price Manipulation: Pumping Bitcoin
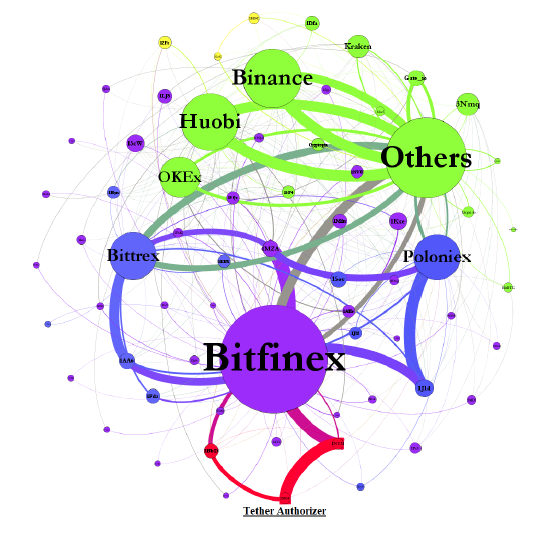
Figure 1. Aggregate Flow of Tether between Major Addresses
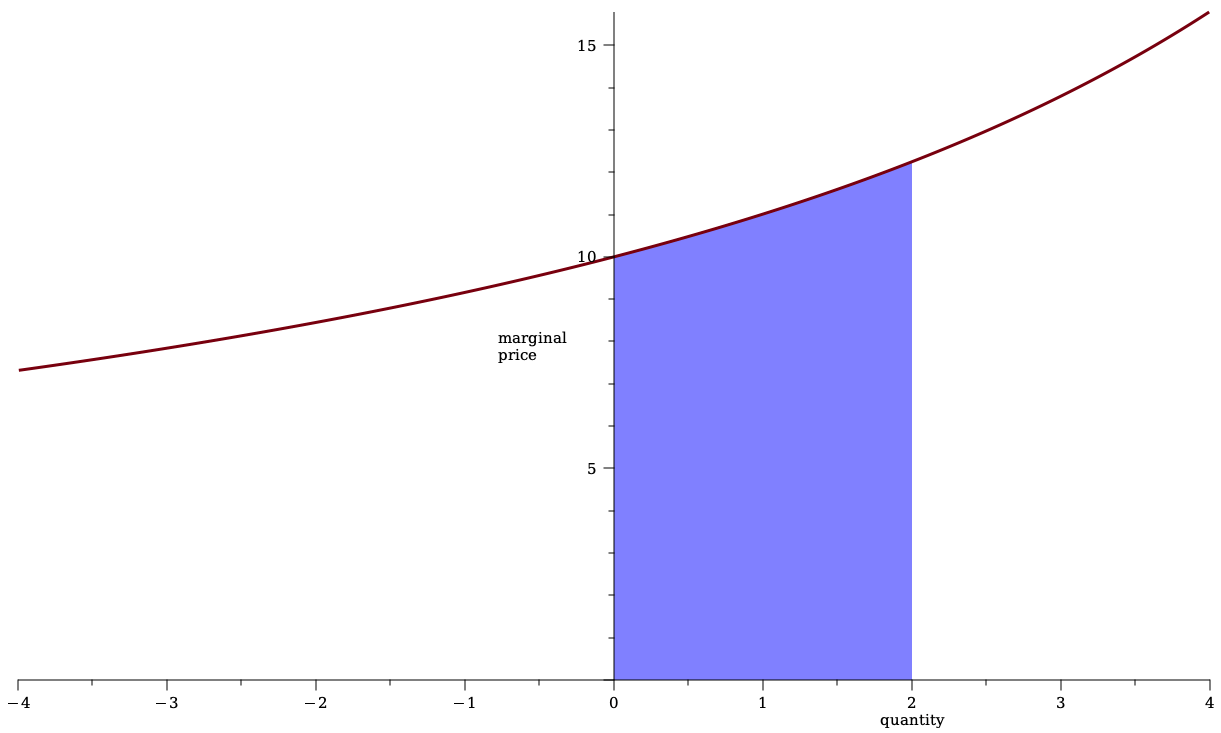
marginal pricing function
quantity \(q\)
price \(p^m(q)\)
Illustration of pricing
Some Pricing Rules from Traditional Markets: Limit Order Book
- Liquidity providers submit sell orders \(s_1(p_1,q_1),\ldots,s(p_n,q_n)\)
- Matching engine sorts order increasing by price
-
someone who wants to buy quantity
\[q\in\left(\sum_{i=1}^{m-1} q_i,\sum_{i=1}^{m} q_i\right]~~~\text{pays}~~\Delta c(q)=\sum_{i=1}^mq_i\cdot p_i.\]
- For a simpler exposition, assume that the price-quantity curve can be expressed by a continuous marginal price function \(\rho(s)\) so that
\[\Delta c(q)=\int_0^q\rho(s) ds.\]
Returns to Liquidity Provision
For fixed balanced volume \(V\) and fee \(F\)
- Larger pool \(\to\) smaller share of fees
- \(\to\) LP expected return \(\searrow\) pool size
Competitive liquidity provision
- \(\Rightarrow\) upper bound on pool size above which LPs lose money
- Here: characterize this amount by the asset's market cap to be deposited to the pool (notation: \(\overline{\alpha}\))
Basics of Liquidity Provision
\[\text{LP payoff}=\text{what I sold it for}-\text{value of net position}+\text{fee income}\]
- \(R\) = asset return
- F = trading fee
- V = balanced volume
- a = size of the liquidity pool
see Lehar and Parlour (2023), Barbon & Ranaldo (2022).
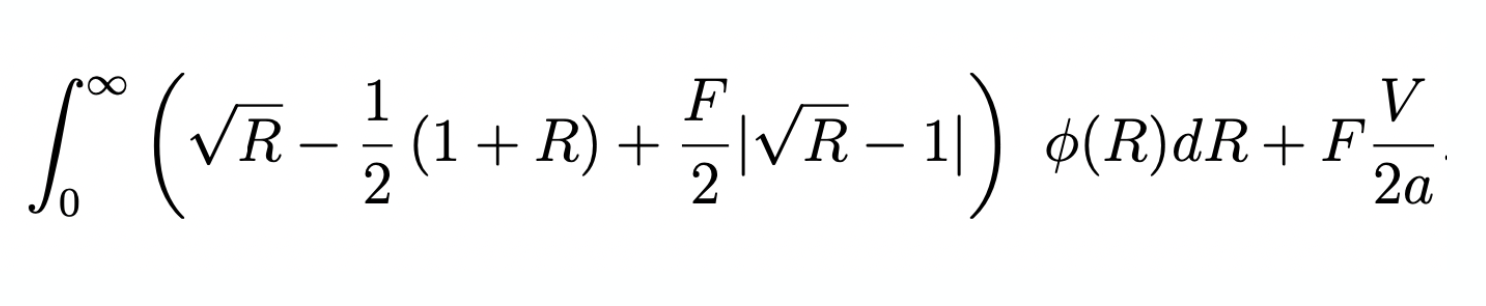
(incremental) adverse selection loss when the return is \(R\)
fees earned
on informed
fees earned
on balanced flow
for reference:
- If the asset price drops by 10% the incremental loss for liquidity providers is 13 basis points on their deposit
- \(\to\) total loss=-10.13%
- If the asset price rises by 10%, the liquidity provider gains 12 basis points less on the deposit
- \(\to\) total gain =9.88%

positional loss
Basics of Liquidity Provision
\[\frac{1}{\text{initial deposit}}\int_0^\infty(\Delta c(q^*)-q^*p_t(R)+F \cdot \Delta c(q^*))~\phi(R)dR +\frac{F p_0 V}{\text{initial deposit}}\ge 0\]
\[\int_0^\infty\left(\frac{\Delta c(q^*)-q^*p_t(R)}{\text{initial deposit}} +F \cdot \frac{\Delta c(q^*)}{\text{initial deposit}}\right)~\phi(R)dR +\frac{F p_0 V}{\text{initial deposit}}\ge 0\]
closed form functions of \(R\) only
(see Barbon & Ranaldo (2022))
\[\underbrace{F \int DV \mu(DV) }_{\text{fees earned on}\atop \text{balanced flow}}+\int_0^\infty\underbrace{(\Delta c(q^*)-q^*p_t(R)}_{\text{adverse selection loss} \atop \text{when the return is {\it R}}} +\underbrace{F \cdot \Delta c(q^*))}_{\text{fees earned}\atop \text{from arbitrageurs}}~\phi(R)dR \ge 0.\]
Basics of Liquidity Provision
\(\Rightarrow\) \(\Delta c(q^*)-q^*p_t(R)\) is also referred to as the "impermanent loss" or "divergence loss"
\(\Delta c(q^*)-q^*p_t(R)=\underbrace{p_t(R)\times(a-q^*) +c+\Delta c(q^*)}_{\text{value of liquidity deposit}}-\underbrace{(p_t(R)a+c)}_{\text{value of buy-} \atop \text{and-hold position}}\)
see Milionis, Moallemi, Roughgarden, and Zhang (2022) for a dynamic analysis of impermanent loss
Basics of Liquidity Provision
Liquidity provision measured as "collective" deposit \(\alpha\) of token's market cap as function of
- balanced volume
- return distribution
(some authors use explicit functions so they can relate it to asset volatility) - fee
\[E[\text{DL}(R)]+F\cdot E[\text{another function of }R]+F\cdot \frac{\text{E[dollar volume]}}{\text{initial deposit}}\ge 0.\]
\[\text{what I sold it for}-\text{value of net position}+\text{fee income} \ge 0 \]
The Decision of the Liquidity Demander
- Wants to trade some quantity \(q\) at cost
\[\text{AMM price impact} +\text{AMM fee}.\]
- two opposing forces for \(F\nearrow\) for liquidity demand
- more liquidity provision
\(\to\) lower price impact - more fees to pay
- more liquidity provision
- Finding: There is a minimal cost fee:
\[F^\pi=\frac{1}{E[|\sqrt{R}-1|/2]+E[DV]}\left(-2q\ E[\text{DL}]+ \sqrt{-2qE[DV]\ E[\text{DL}]}\right).\]
this is from Malinova and Park (2023); similar result is in Hasbrouk, Riviera, Saleh (2023)
Model Summary
- Have: equilibrium choice for liquidity provision.
Useful feature: can express liquidity by % market cap of token/asset
- Can measure cost for liquidity demanders to use AMM.
- Know: fee that maximizes liquidity demander benefit (\(\not=0\))
The Pricing Function
Liquidity Deposit \(\Rightarrow\) slope of the price curve

- Most common form of AMM liquidity rule is Constant Product Pricing
\[L(a,c)=a\cdot c~\Rightarrow~a\cdot c= (a-q)\cdot (c+\Delta c).\] - Total cost of trading \(q\) \[\Delta c=\frac{cq}{a-q}.\]
- Price per unit \[p(q)=\frac{c}{a-q}.\]
- Average spread paid\[\frac{p(q)}{p(0)}-1=\frac{q}{a-q}.\]
- makes asset and cash deposit
- more deposits flatter price curve
- attracts more volume
- but larger "positional" loss when prices move
The Pricing Function (just a little more)
- A limit order book has a marginal price function \(\rho(q)\) so that \[\Delta c(q)=\int_0^q\rho(s) ds.\]
- We can do that here, too: for
\[\rho(q)=\frac{ac}{(a - q)^2},\]
we have \[\int_0^q \frac{ac}{(a - s)^2}ds=\frac{cq}{a-q}.\] - \(\to\) Constant Product = special case of a limit order book.
The Pricing Function (almost done, just one more thing)
- Suppose we start with a price \(P\) and end with a price \(P'=R\cdot P\).
- We know by definition
\[P=\frac{c}{a},~P'=\frac{c'}{a'},~L=\sqrt{ac},~L=\sqrt{a'c'}.\]
- Then it holds that \[a=\frac{L}{\sqrt{P}},~c=L\sqrt{P},~a'=\frac{L}{\sqrt{P'}},~c'=L\sqrt{P'}.\]
- For the price to move from \(P\) to \(P'\), quantities \(q,\Delta c\) change hands.
- Therefore \(a'=a-q,~c'=c+\Delta c\)
- Combine with the above \[a-q=\frac{L}{\sqrt{P'}}~\Leftrightarrow~q=L\left(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{P'}}\right).\]
- do the same for \(\Delta c\) \[\Delta c= L\left(\sqrt{P'}-\sqrt{P}\right).\]
- the per unit price for the trade of \(\Delta x\) is \[\frac{\Delta c}{q}=\sqrt{PP'}=P\sqrt{R}.\]
- \(\to\) avg price is the geometric mean of the prices
AMMs continue to evolve: UniSwap v3
Basic idea:
- allow different fees (let's ignore)
- don't supply liquidity for entire price range \((0,\infty)\) but only \([p_a,p_b]\)
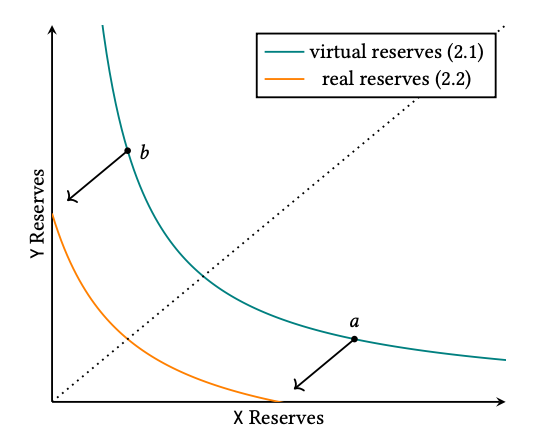
- idea: project the iso-liquidity curve back to the axes
- price in this range is determined by constant product rule
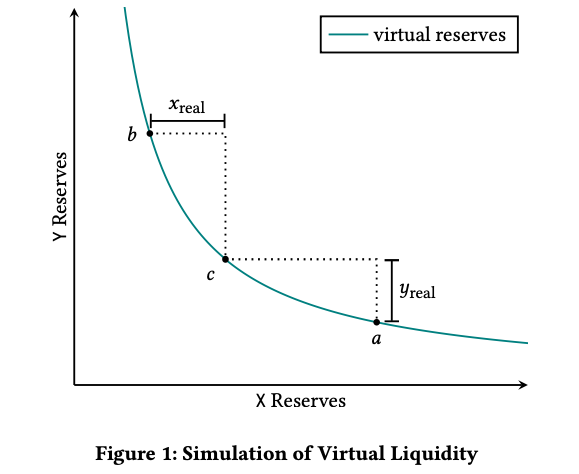
Source:" Uniswap v3 Core," Adams, Zinsmeister, Salem, Keefer, Robinson (2021)
- current price at point \(c\): \(p_c\)
- \(x_{\text{real}}=\) max of \(X\) you buy
- \(y_{\text{real}}=\) max of \(Y\) you buy
- pricing effectively occurs on a grid
- it's not straightforward to describe the pricing function without lots of new notation
Some UniSwap v3 maths (Barbon & Ranaldo 2023)
Source: Elsts (2021) "Liquidity Math in UniSwap v3"
- We are interested in "virtual limit orders"
- for selling known \(x\Rightarrow y=0\) (only sell) have known \(P,x,y,p_a\):
- what is the (ask) price \(p_b\)?
- for selling up to price \(p_b\) \(\Rightarrow y=0\) (only sell) have known \(P,y,p_a,p_b\):
- what is the quantity \(x\)?
- for selling known \(x\Rightarrow y=0\) (only sell) have known \(P,x,y,p_a\):
- When the price is in interior of \((p_a,p_b)\) liquidity provided "to the left" of the price must coincide with liquidity provided to the right.
- We can derive conditions \[x=L\ \frac{\sqrt{p_b}-\sqrt{P}}{\sqrt{p_b}\sqrt{P}}\]
\[y=L\ (\sqrt{P}-\sqrt{p_a})\]
- \(\tilde{x},\tilde{y}\) the "real" reserves, \(x,y\) the virtual reserves
- \(P\) the price of "\(x\)" (asset) in "\(y\)" (cash), with \(P\in[p_a,p_b]\)
- \(L\) the liquidity
- Constant product function: \(L=\sqrt{xy}\)
- And then \[L^2=\left(\tilde{x}+\frac{L}{\sqrt{p_b}}\right)\left(\tilde{y}+L\sqrt{p_a}\right).\]
- At the price bounds, the real amounts are either \(x=0\) or \(y=0\). We can derive conditions \[x=L\ \frac{\sqrt{p_b}-\sqrt{p_a}}{\sqrt{p_b}\sqrt{p_b}}\]
\[y=L\ (\sqrt{p_b}-\sqrt{p_a})\]
Problem: MEMPOOL Frontrunning is intrinsically profitable
\(X\)
\(Y\)
normal trade: sell \(x\) \(\to\) get \(y'\)
\(Y-y'\)
\(X+x\)
front-running:
- front-runner: sells \(x\) \(\to\) gets \(y'\)
- front-run: sells \(x\) \(\to\) gets \(y''\)
- front-runner: buys \(x\) \(\to\) pays \(y''\)
\(Y-y'-y''\)
\(X+2x\)
\(y'>y''~\Rightarrow\)
front-running is intrinsically profitable
Disclaimer:
- this problem is well-known
- fees can mitigate it
- several protocols such as the latest iteration by Balancer try to combat it
Dark side of DEx trading: Miner extractable value
Application 1: decentralized trading with automated market makers













Problems:
- How to get liquidity?
- How do you attract traders?
lesser problem because
- tokens trade elsewhere
- arbitrage creates activity
Common solution: create a reward token! Here's how this works
Step 4: users receive a reward token based on the time that they lock up the "receipt" token

Step 3: users lock up the "receipt" token in a smart contract




Step 2: users contribute liquidity and get a "receipt" token

Step 1: create reward tokens and deposit into a smart contract













borrow
provide collateral
Application: Pool-based borrowing and lending
Application 2: decentralized Borrowing and Lending
Same problems as with trading:
- How to get liquidity?
- How do you attract borrowers?
But: in contrast to trading, here you need both!
liquidity \(\nearrow\)
volume \(\nearrow\)
protocol fees \(\nearrow\)
token value \(\nearrow\)
Platform economics is tricky:
- What's the product?
- How do you get it started?
- How do you get people to contribute?
- How do you earn money?
Without intermediaries:
platform economics!
incentives for both?
What value do these tokens have?
- Functionality:
- fee levels for AMMs
- decision to deploy on other chains
- key threshold values for lending
- Monetary value
- implicit claims on "protocol" income
- implicit claim on reserve pools
Vampire Attacks and Other Shenanigans

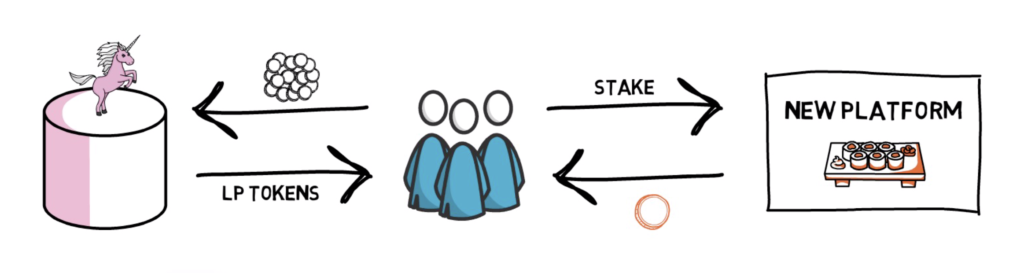
Source: https://finematics.com/vampire-attack-sushiswap-explained/
- Vampire Attack:
- syphon liquidity from a different protocol
- using your own token!!!
- Mechanism:
- deposit in UniSwap, receive LP token
- deposit LP token to Sushi, receive rewards
- liquidate LP token and migrate original liquidity to Sushi = "suck out the blood from UniSwap"
another common trick:
- pump the price of the reward tokens
- \(\Rightarrow\) "yields" often exceed 500%