Learning from DeFi: Would Automated
Market Makers Improve Equity Trading?

Katya Malinova and Andreas Park

Agenda

Very brief overview of Automated Market Makers
Liquidity supply and demand
Research question: what if we used AMMs for equities?
- theory: liquidity provision & demand
- data: implementation & trading costs

Why did we write this paper?

Current U.S. mindset: everything crypto-related is evil
GG/S.E.C.: "We made up a new market institution that is so awesome that it'll save (retail) investors $1.5B per year"

Seriously?

0. Cynicism aside - big question: Can we improve liquidity for smaller listings?

Some Motivation

Blockchain: borderless general purpose value and resource management tool

Basic Idea

DeFi: financial applications that run on blockchains

$\Rightarrow$ brought new ideas and tools

one new market institution: automated market makers

Trading Infrastructure

payments network

Stock Exchange

Clearing House

custodian

beneficial ownership record

seller

buyer

Broker

Exchange

Internalizer

Wholeseller

Darkpool

Venue

Settlement

Application: decentralized trading with automated market makers

AMM Pricing

AMMs require liquidity deposits
Deposits:
- $a$ units of an asset (e.g. a stock)
- $c$ units of cash

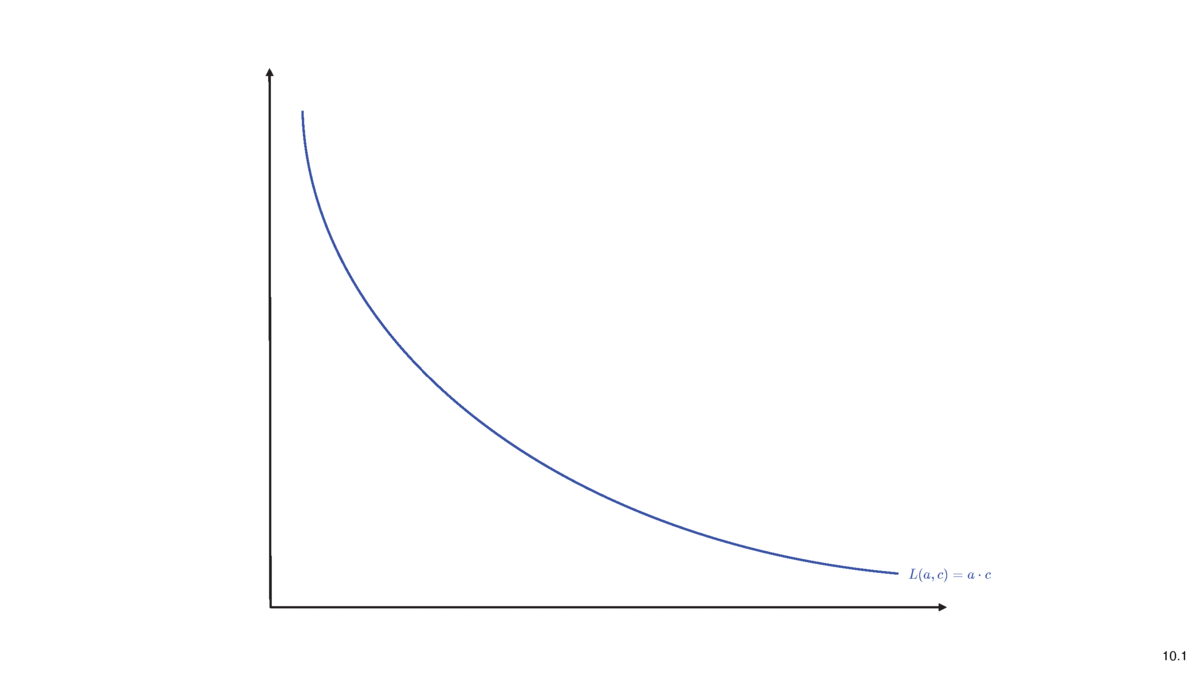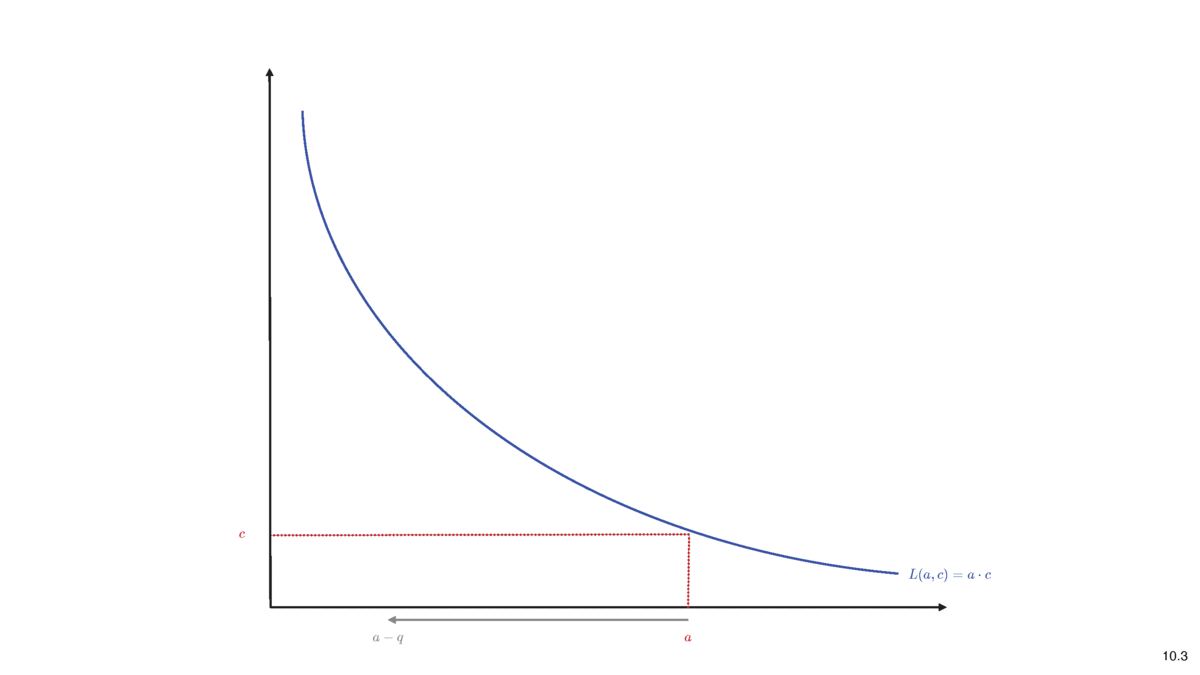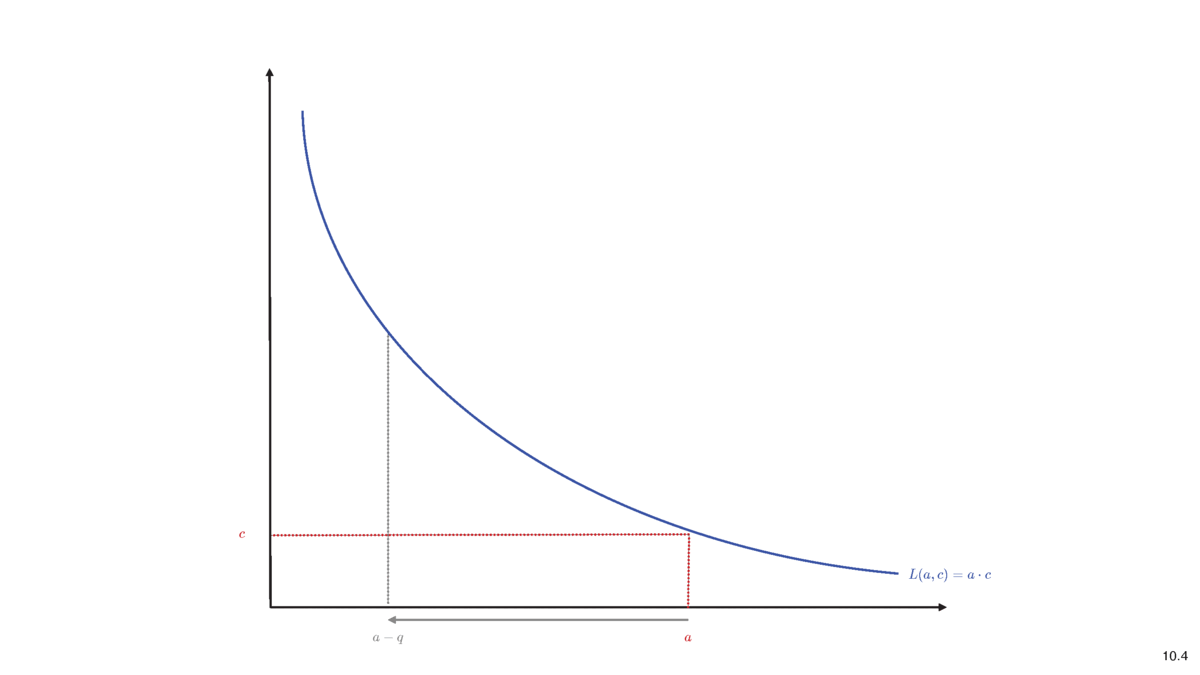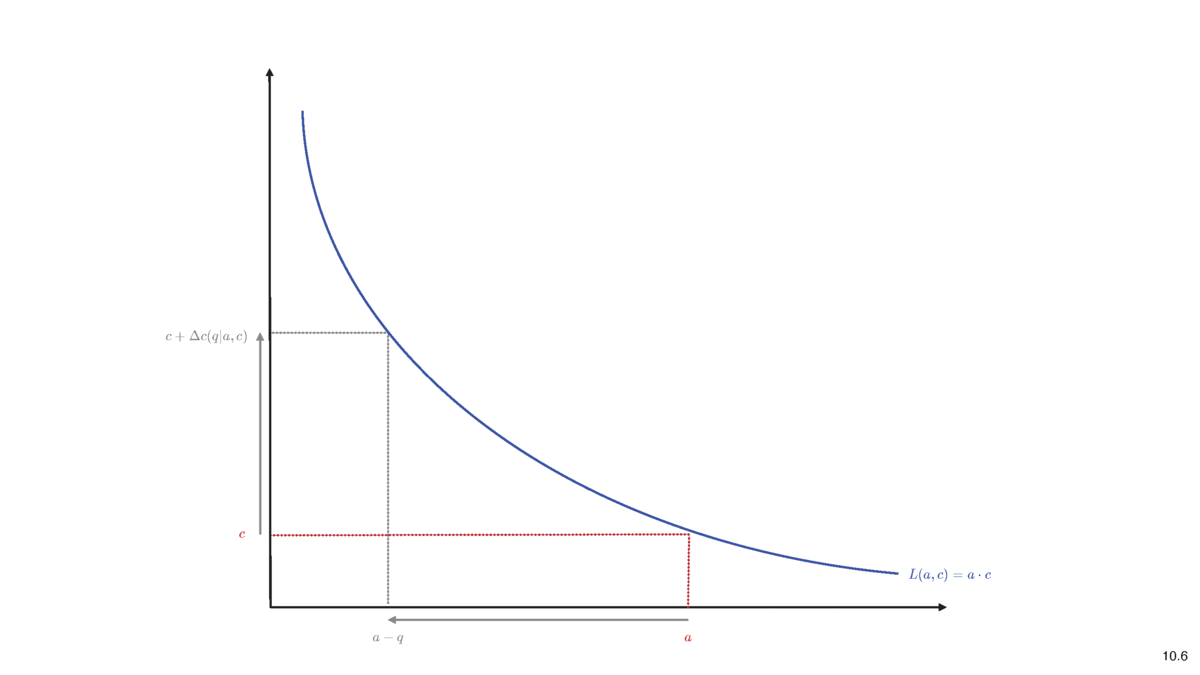
Constant Liquidity (Product) AMM

Purchase $q$ of asset
Deposit cash $\Delta c (q)$ into liquidity pool, extract $q$ of shares
Idea of pricing: liquidity before trade $=$ after trade
\[L(a,c)=L(a-q,c+\Delta c)\]

AMMs require liquidity deposits
Deposits:
- $a$ units of an asset (e.g. a stock)
- $c$ units of cash

Key Components

Our question:
1. Can an economically viable AMM be designed for current equity markets?
2. Would such an AMM improve current markets?

pooling of liquidity

pro-rated
- fee income
- risk

Liquidity providers:
- use existing assets to earn passive income

Liquidity demanders:
- predicatable price
- continuous trading
- ample liquidity

Liquidity Supply and Demand in an Automated Market Maker

The Pricing Function

Liquidity Deposit $\Rightarrow$ slope of the price curve

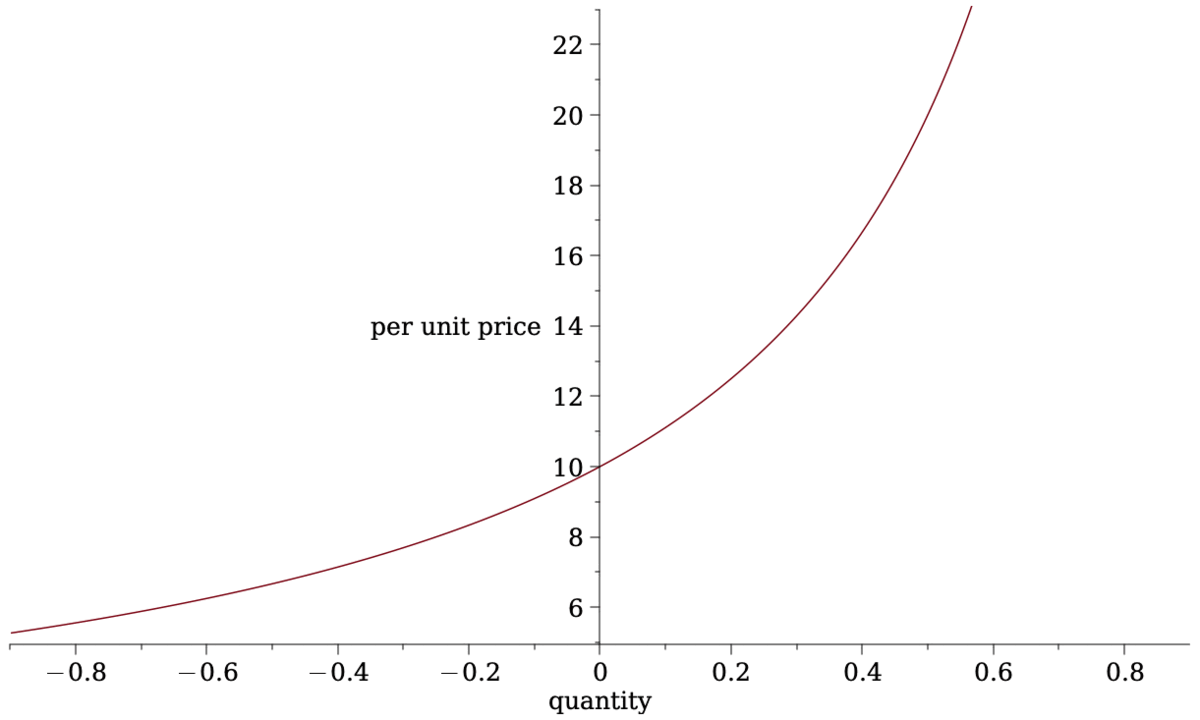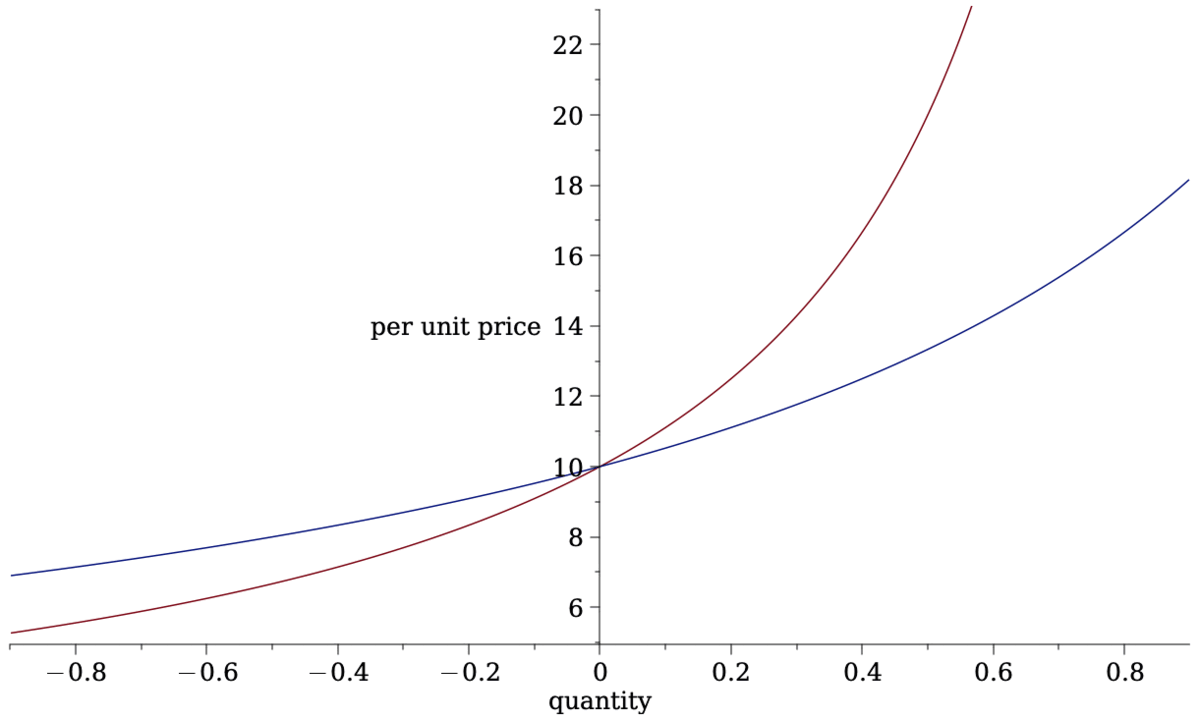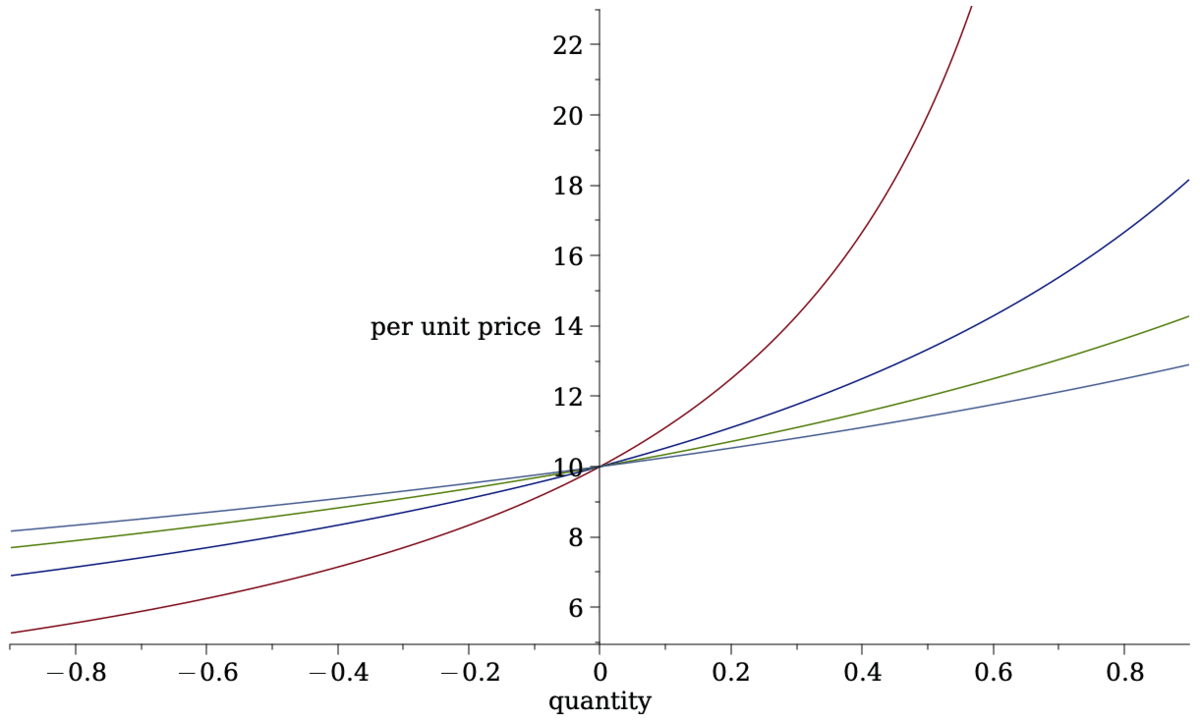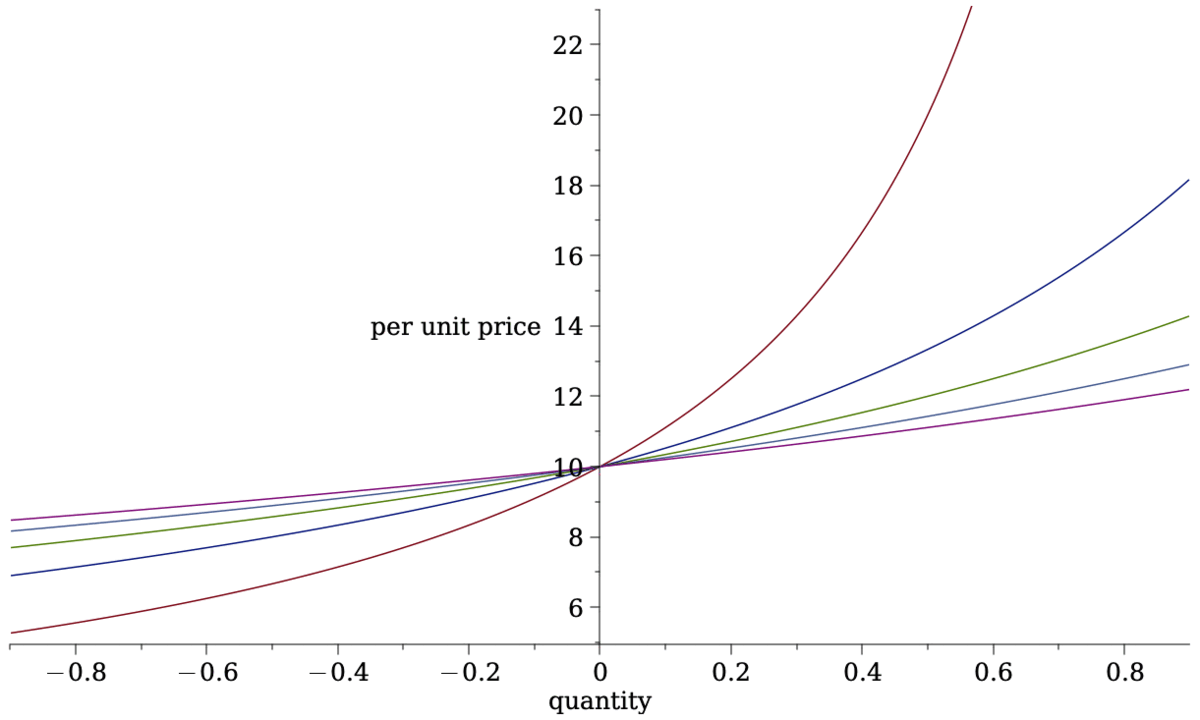
Most common form of AMM liquidity rule is Constant Product Pricing
\[L(a,c)=a\cdot c~\Rightarrow~a\cdot c= (a-q)\cdot (c+\Delta c).\]
Total cost of trading $q$ \[\Delta c=\frac{cq}{a-q}.\]
Price per unit \[p(q)=\frac{c}{a-q}.\]
Average spread paid\[\frac{p(q)}{p(0)}-1=\frac{q}{a-q}.\]

makes asset and cash deposit
more deposits flatter price curve
- attracts more volume
- but larger "positional" loss when prices move

Basics of Liquidity Provision

\[\underbrace{F p_0 V}_{\text{fees earned on balanced flow}}+\int_0^\infty\underbrace{(\Delta c(q^*)-q^*p_t(R)}_{\text{adverse selection loss when the return is $R$}} +\underbrace{F \cdot \Delta c(q^*))}_{\text{fees earned from arbitrageurs}}~\phi(R)dR \ge 0.\]

$q^* $ is what arbitrageurs trade to move the price to reflect $R$

fundamental value up
- $\Rightarrow$ price up
  - $\Rightarrow$ sell the asset for less than its worth
fundamental value down
- $\Rightarrow$ price up
  - $\Rightarrow$ buy the asset for more than its worth

Basic idea of liquidity provision: earn more on balanced flow than what you lose on price movement

\[\text{fee income} +\underbrace{\text{what I sold it for}-\text{value of net position}}_{\text{adverse selection loss}} \ge 0 \]

in AMMs:
protocol fee

in tradFi: bid-ask spread

Basics of Liquidity Provision

\[\int_0^\infty\underbrace{(\Delta c(q^*)-q^*p_t(R)}_{\text{adverse selection loss when the return is $R$}} +\underbrace{F \cdot \Delta c(q^*))}_{\text{fees earned from arbitrageurs}}~\phi(R)dR +\underbrace{F p_0 V}_{\text{fees earned on balanced flow}}\ge 0\]

\[\frac{1}{\text{initial deposit}}\int_0^\infty(\Delta c(q^*)-q^*p_t(R)+F \cdot \Delta c(q^*))~\phi(R)dR +\frac{F p_0 V}{\text{initial deposit}}\ge 0\]

\[\int_0^\infty\left(\frac{\Delta c(q^*)-q^*p_t(R)}{\text{initial deposit}} +F \cdot \frac{\Delta c(q^*)}{\text{initial deposit}}\right)~\phi(R)dR +\frac{F p_0 V}{\text{initial deposit}}\ge 0\]

closed form functions of $R$ only
(see Barbon & Ranaldo (2022))

Sidebar: we can quantify how much a PASSIVE LP loses when the price moves by $R$

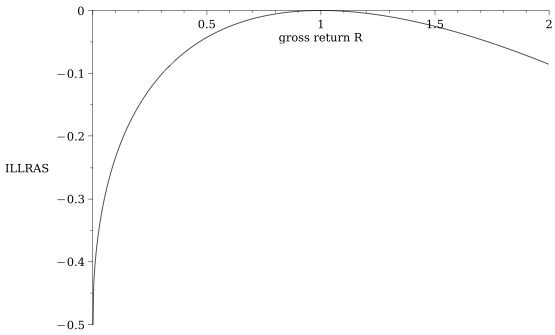
for orientation:

If the stock price drops by 10% the incremental loss for liquidity providers is 13 basis points on their deposit
- $\to$ total loss=-10.13%
If the stock price rises by 10%, the liquidity provider gains 12 basis points less on the deposit
- $\to$ total gain =9.88%

\[\frac{\text{adverse selection loss when the return is $R$}}{\text{initial deposit}}=\sqrt{R}-\frac{1}{2}(R+1)\]

see Barbon & Ranaldo (2022)

Basics of Liquidity Provision

Liquidity provision measured as "collective" deposit $\alpha$ of firm's market cap as function of

balanced volume
asset volatility/return distribution
fee

\[E[\text{IILRAS}(R)]+F\cdot E[\text{another function of }R]+F\cdot \frac{\text{dollar volume}}{\text{initial deposit}}\ge 0.\]

\[\text{what I sold it for}-\text{value of net position}+\text{fee income} \ge 0 \]

The Decision of the Liquidity Demander

Wants to trade some quantity $q$.
Is better off with AMM relative to traditional market if

\[\text{bid-ask spread}\ge\text{AMM price impact} +\text{AMM fee}.\]

two opposing forces for $F\nearrow$ for liquidity demand
- more liquidity provision
  $\to$ lower price impact
- more fees to pay
Finding: There is an optimal fee:

\[F^\pi=\frac{1}{E[|\sqrt{R}-1|/2]+V}\left(-2q\ E[\text{ILLRAS}]+ \sqrt{-2qV\ E[\text{ILLRAS}]}\right).\]

Model Summary

Have: equilibrium choice for liquidity provision.
Useful feature: measure by % market cap
Measure: benefit for liquidity demanders to use AMM.
Know: fee that maximizes liquidity demander benefit ($\not=0$)
Next: Calibrate to stock markets
- Optimal fees?
- Feasible?
- Empirical benefits?

How we think of the Implementation of an AMM for our Empirical Analysis

Approach: daily AMM deposits

AMMs close overnight.
Market: opening auction $\to$ $p_0$
Determine: optimal fee; submit liquidity $a,c$
at ratio $p_0=a/c$ until break even $\alpha=\overline{\alpha}$
Liquidity locked for day
At EOD release deposits and fees
Back to 1.

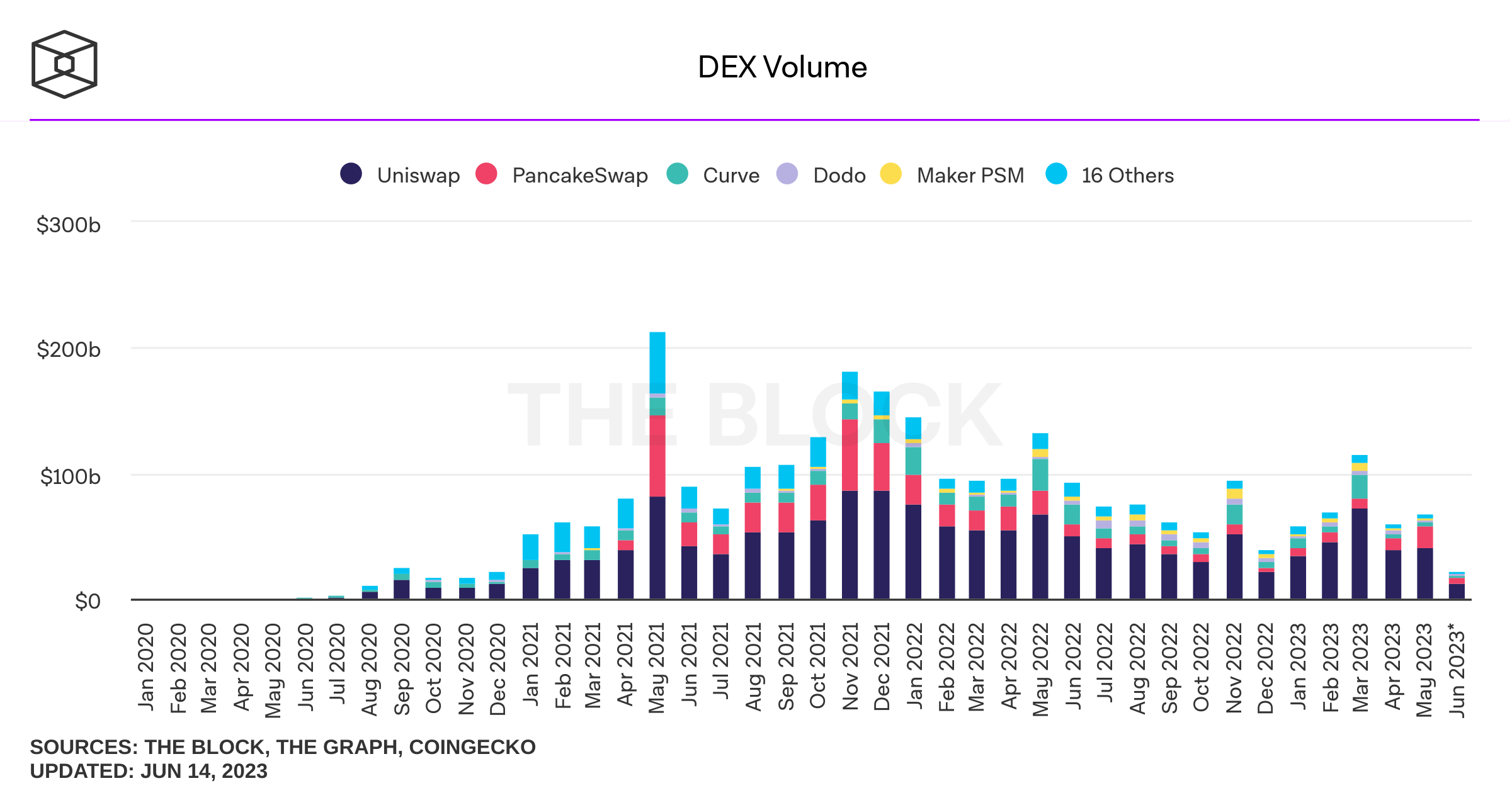
Background on Data

Special Consideration 1: What volume?

some volume may be intermediated
with AMMs: no need for intermediation
$\to$ intermediate volume should disappear
$\to$ use volume/2

Special Consideration 2: What's $q$ (the representative order size)?

use average per day
take long-run average + 2 std of daily averages
(also avg $\times 2$,$\times 4$, depth)

All displayed data CRSP $\cap$ WRDS

CRSP for shares outstanding
WRDS computed statistics for
- quoted spreads (results similar for effective)
- volume
- open-to-close returns
- average trade sizes, VWAP
Time horizon: 2014 - March 2022
Exclude "tick pilot" period (Oct 2016-Oct 2018)
All common stocks (not ETFs) (~7550).
Explicitly not cutting by price or size
All "boundless" numbers are winsorized at 99%.

AMMs that's true to the "model"

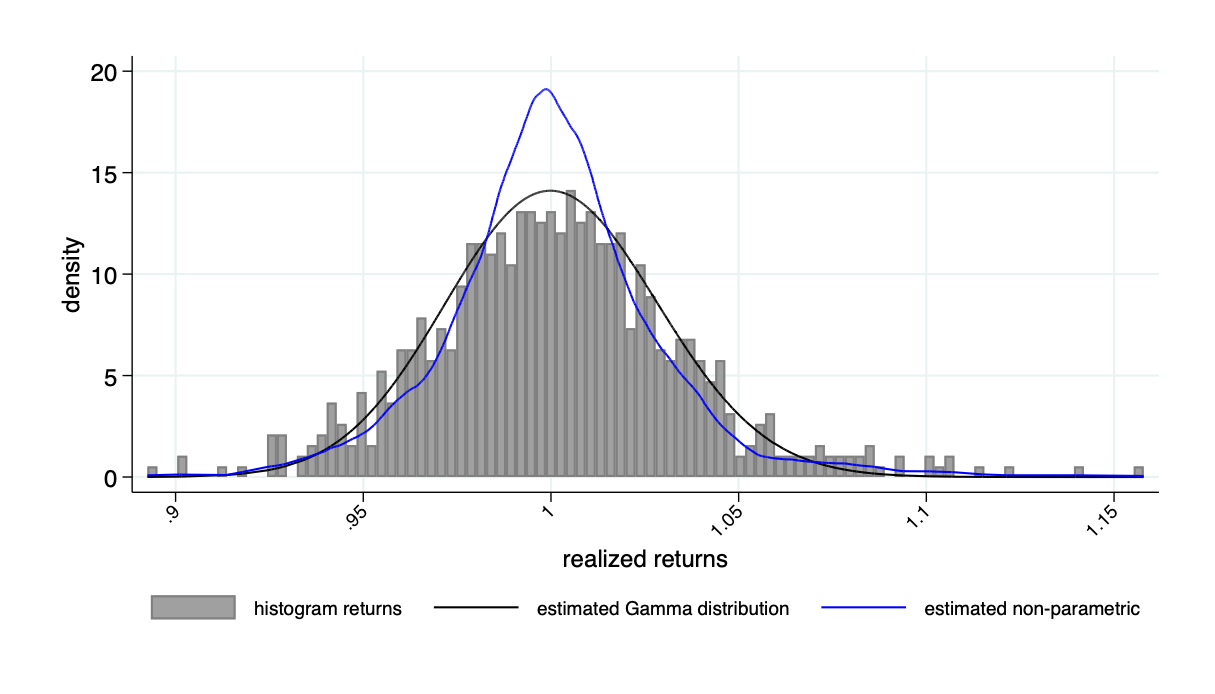
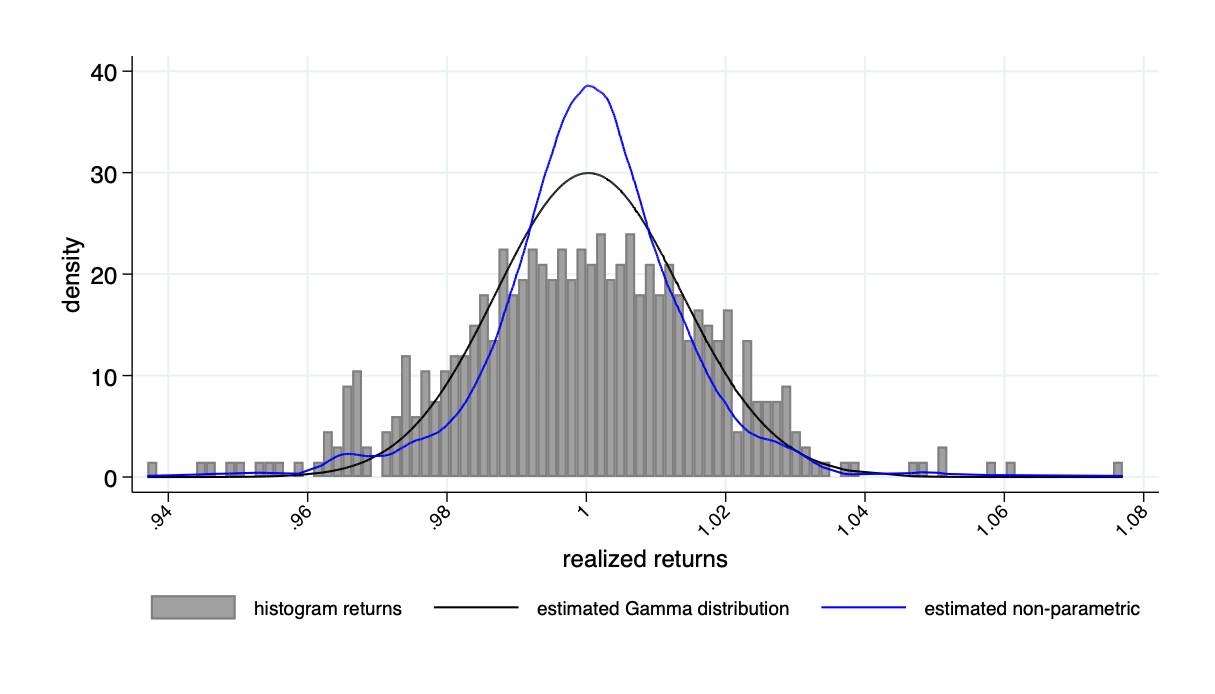
Return distribution example: Microsoft

Return distribution example: Tesla

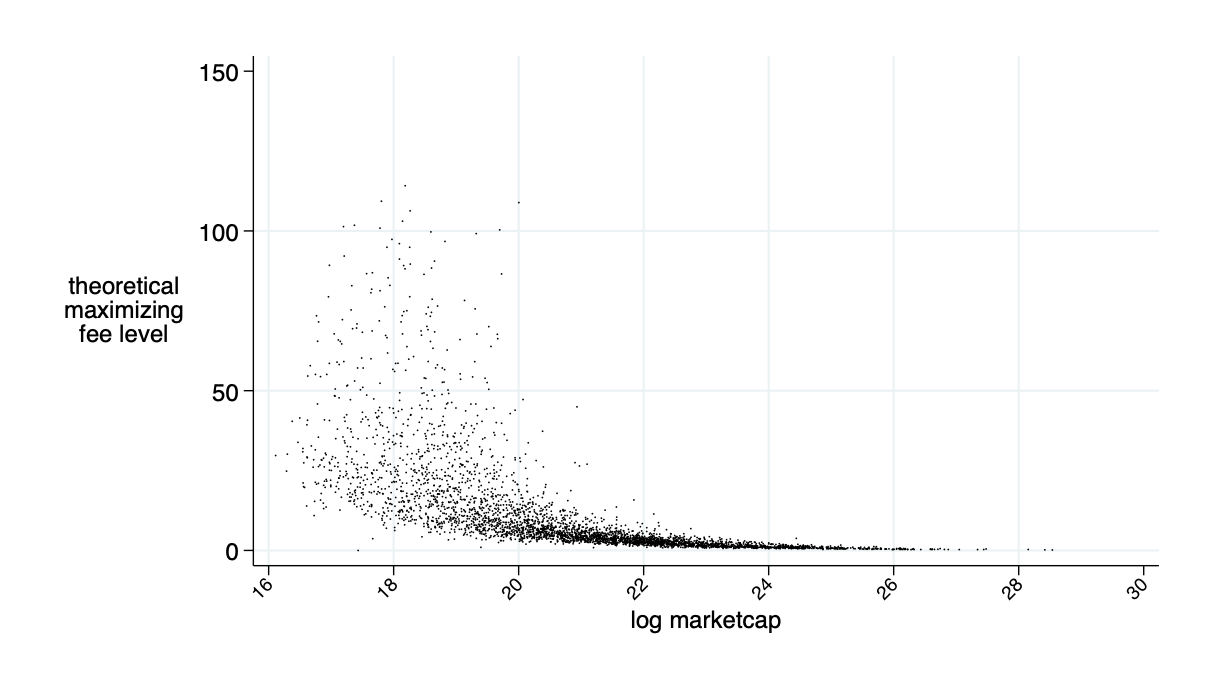
average $F^\pi=11$bps

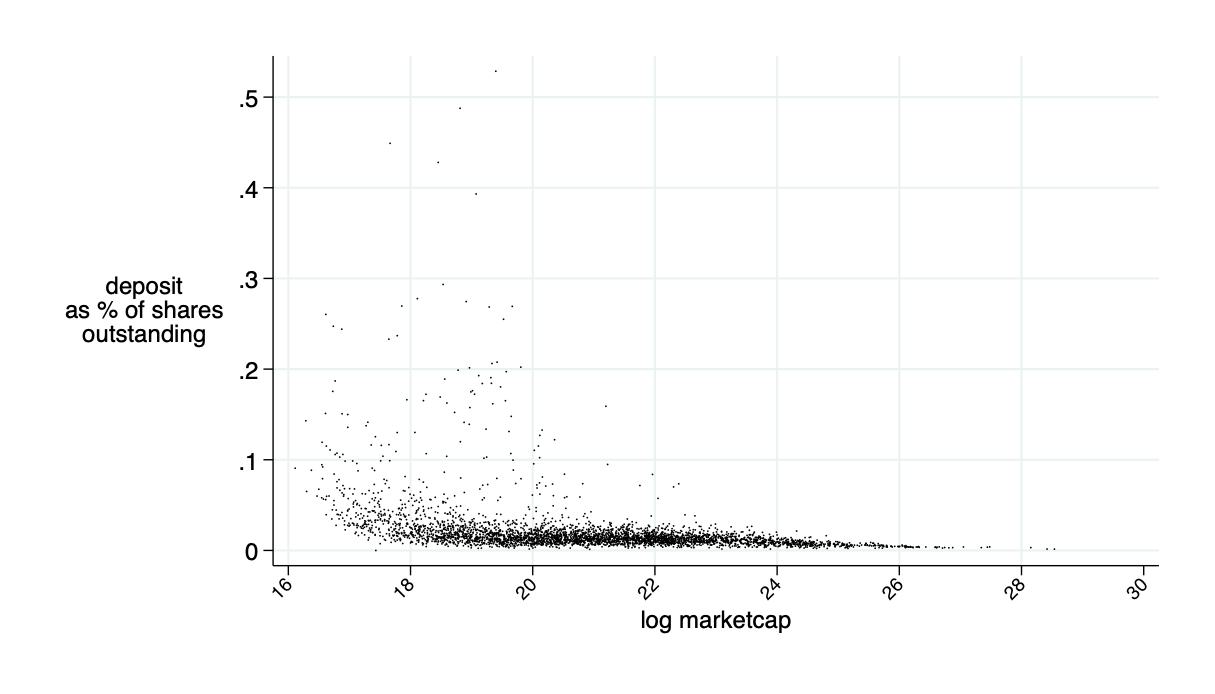
$\bar{\alpha}\approx 2\%$

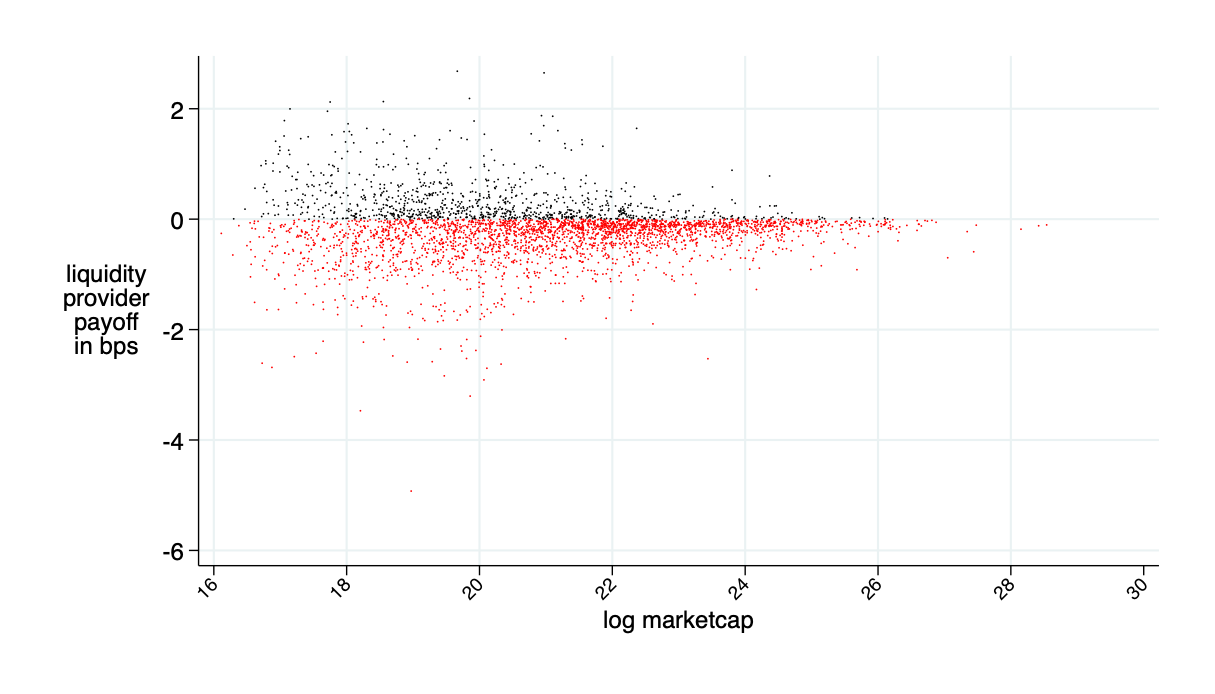
almost break even on average (average loss 0.2bps $\approx0$)

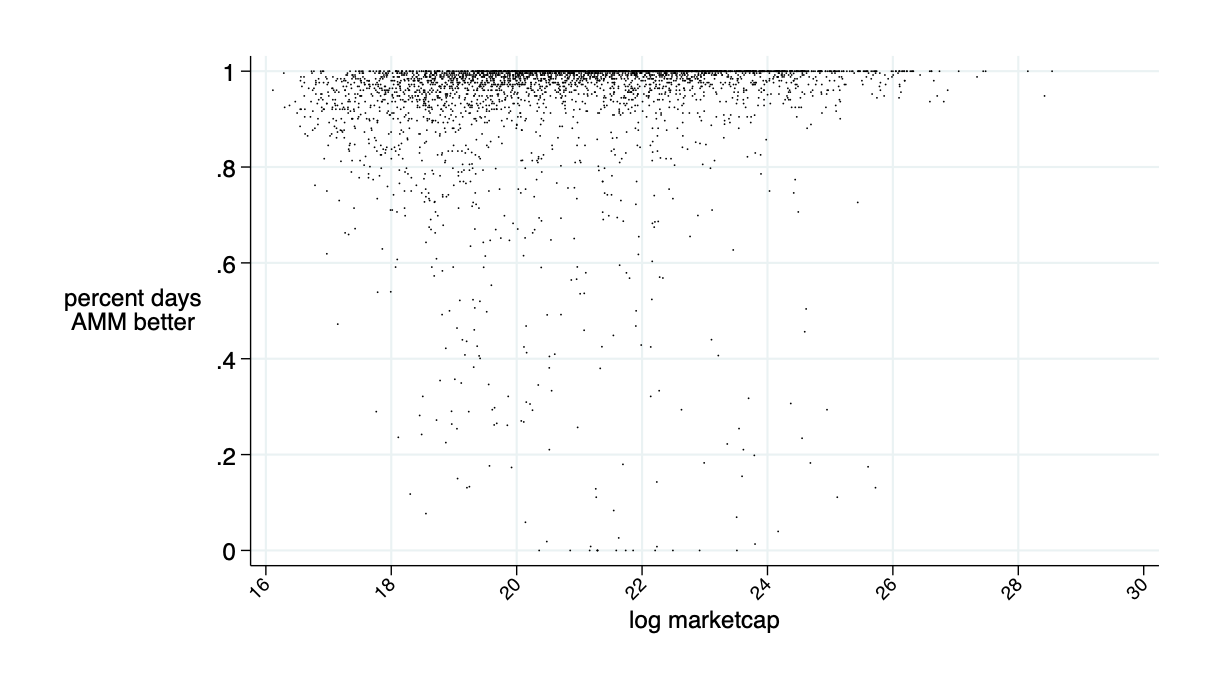
average: 94% of days AMM is better than LOB

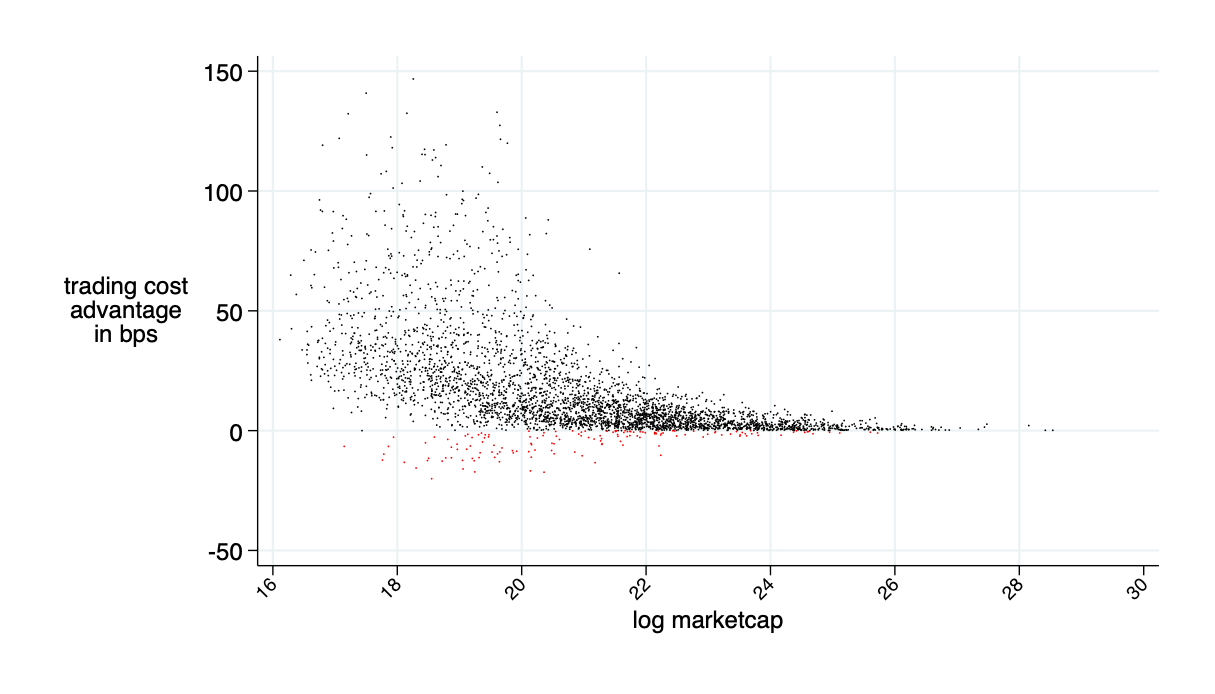
average savings: 16 bps

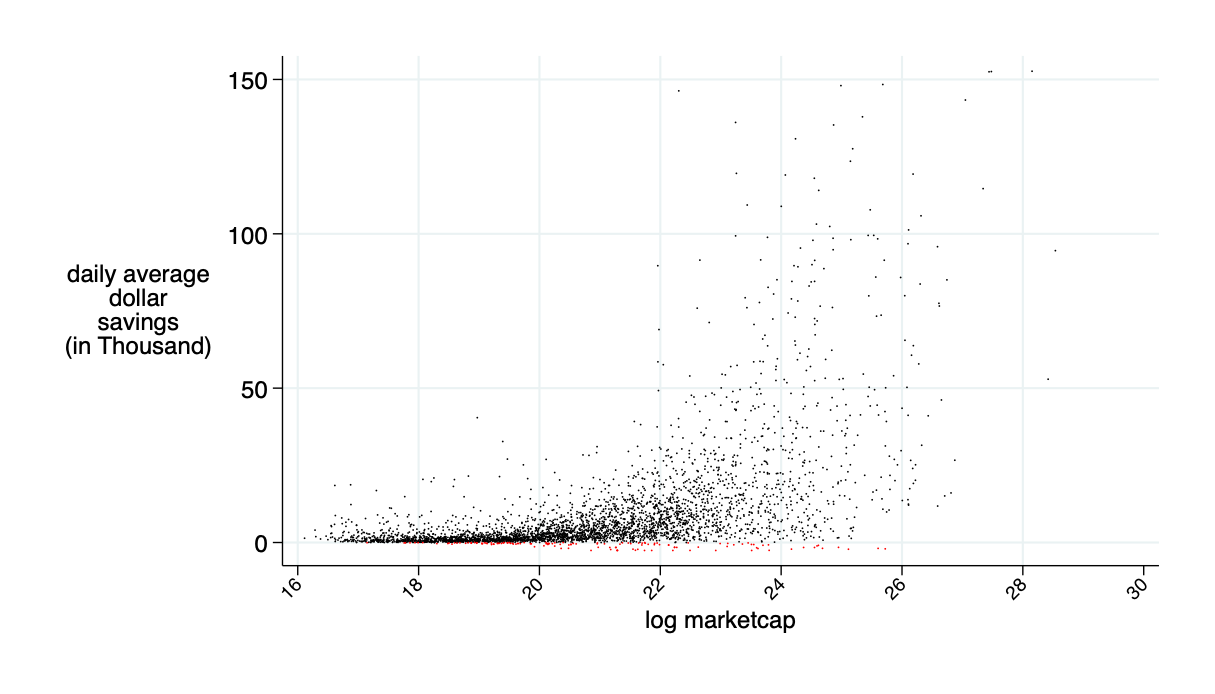
average daily: $9.5K

saves around 45% of transaction costs (measured in bid-ask spread)

average annual saving: $2.4 million

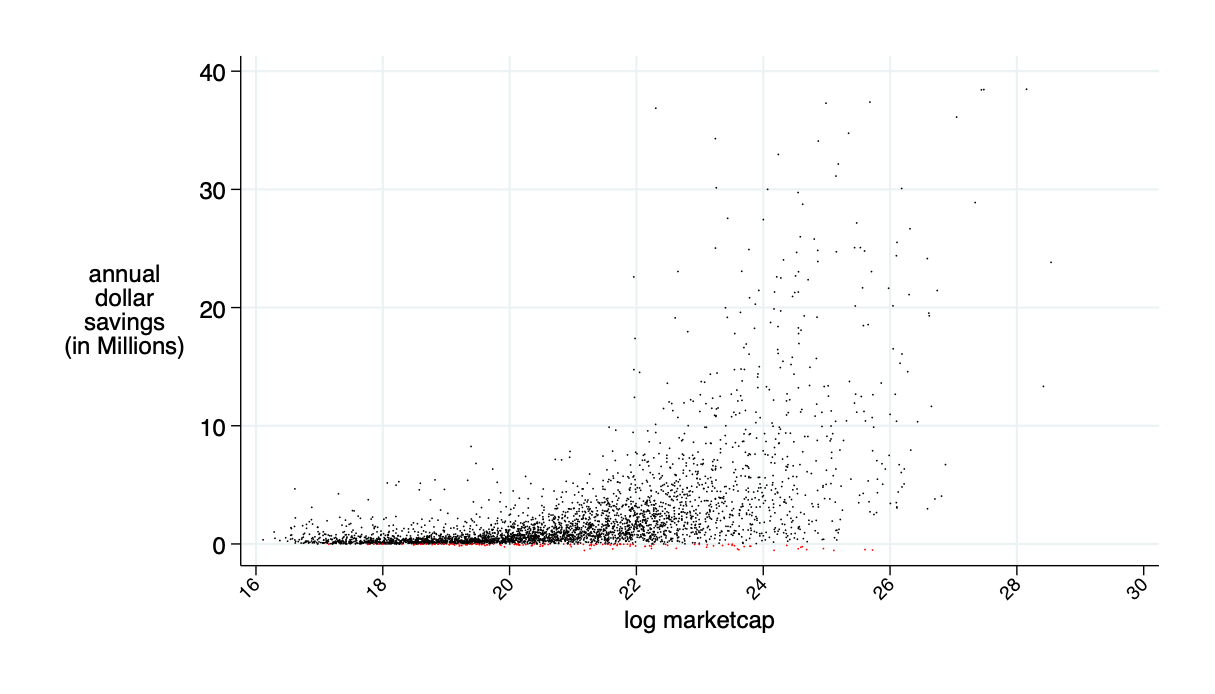
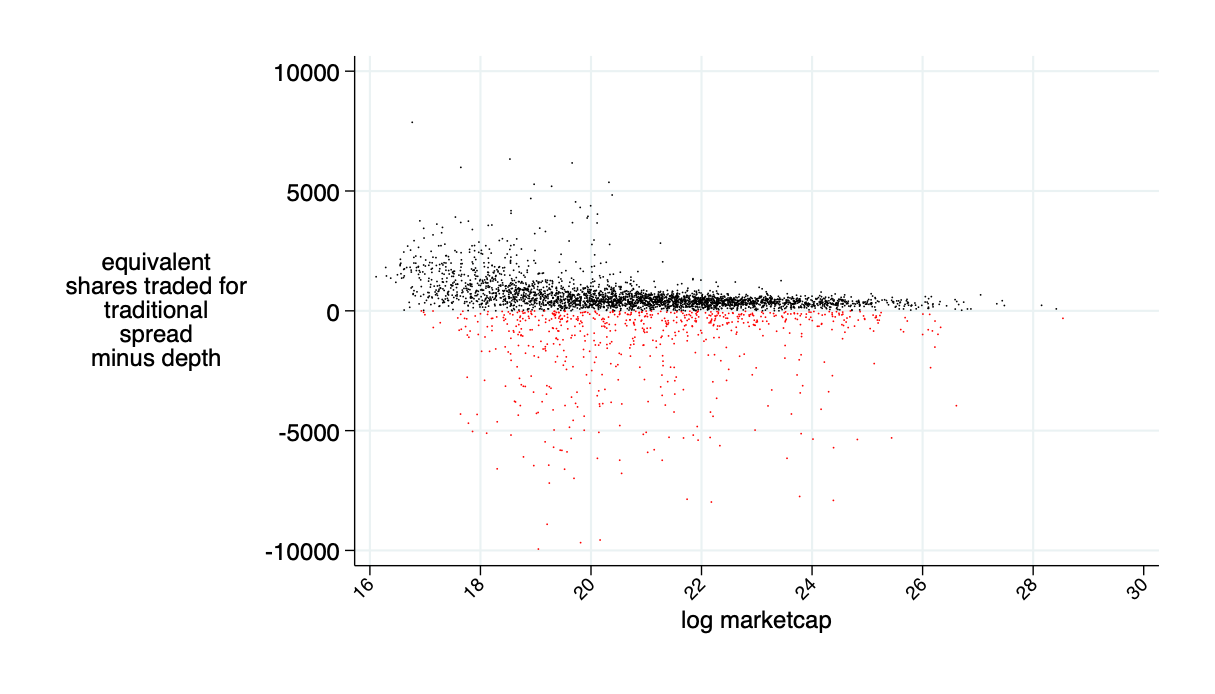
Optimally Designed AMMs with
"ad hoc" one-day backward look

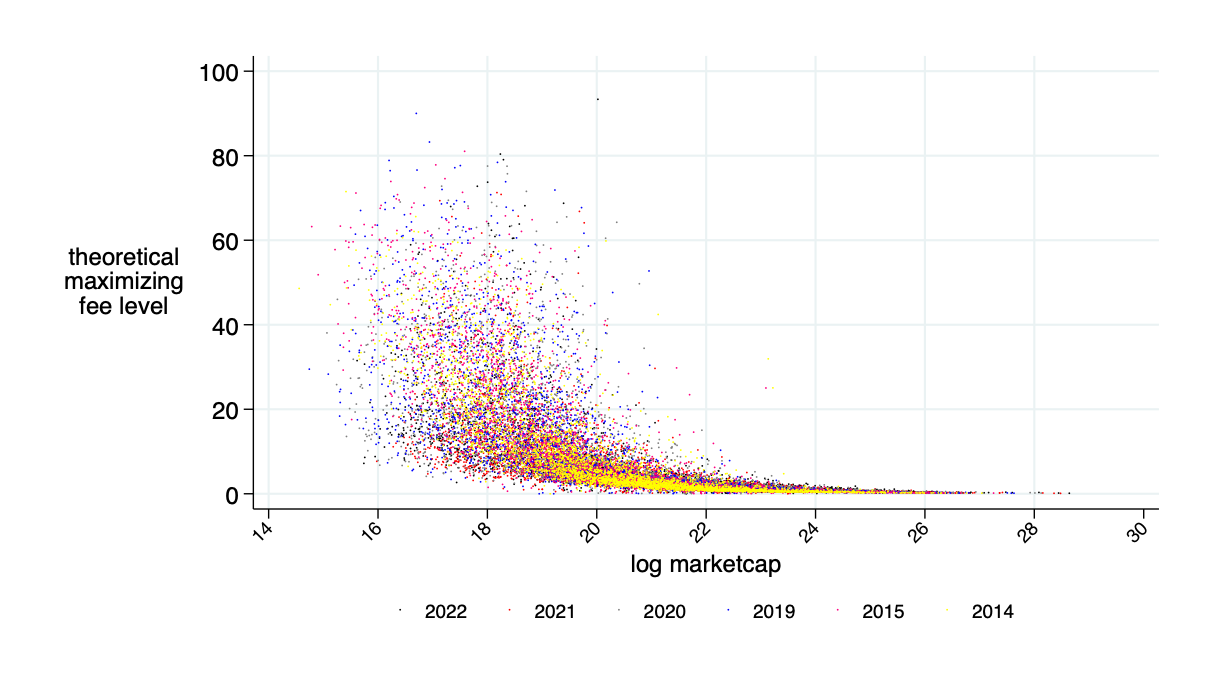
Optimal fee $F^\pi$

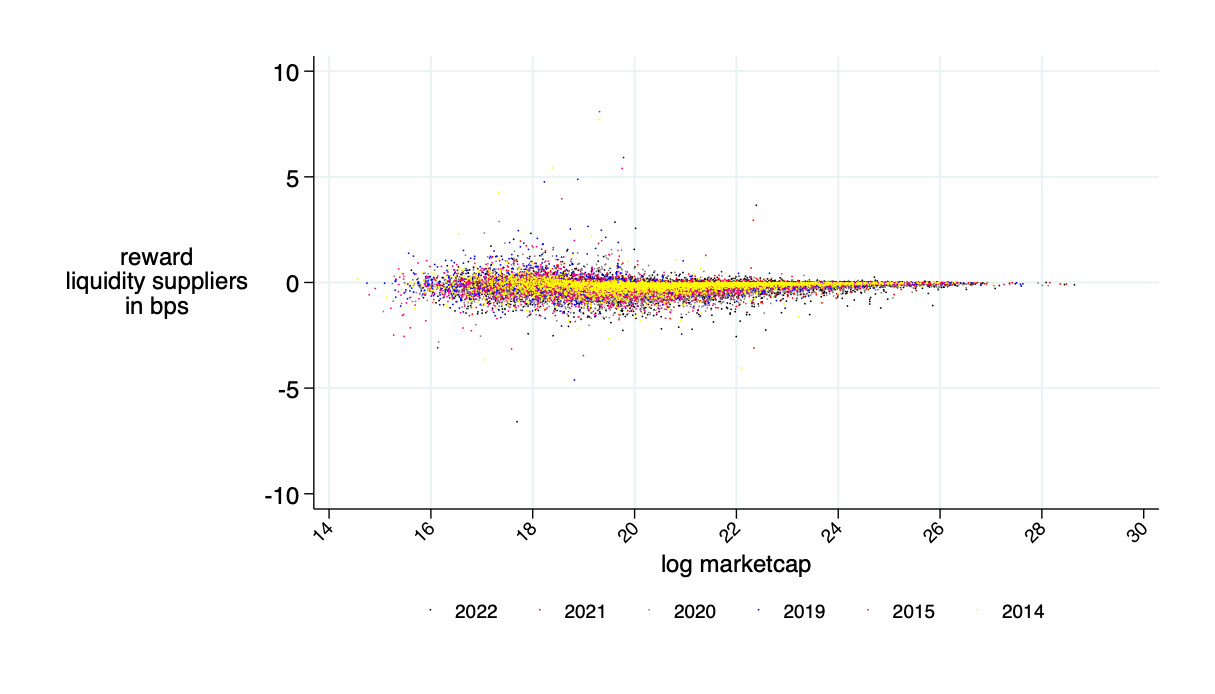
average benefits liquidity provider in bps (average=0)

Insight: Theory is OK - LP's about break even

$\overline{\alpha}$ for $F=F^\pi$

Need about 10% of market cap in liquidity deposits to make this work

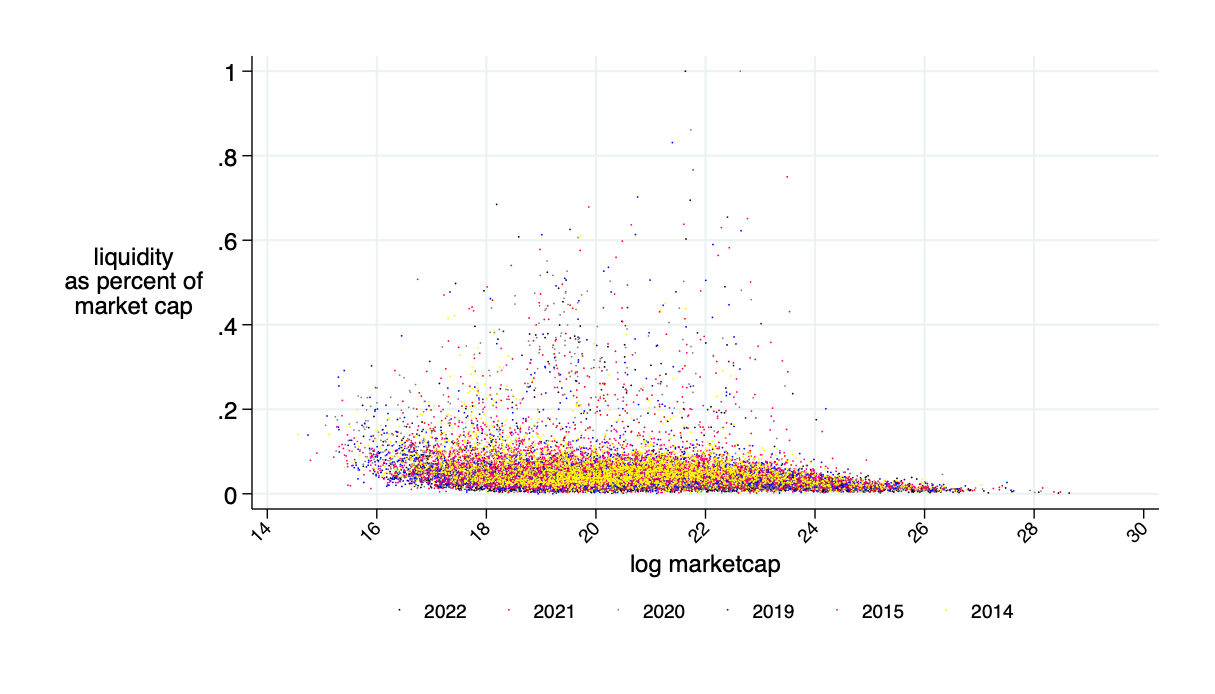
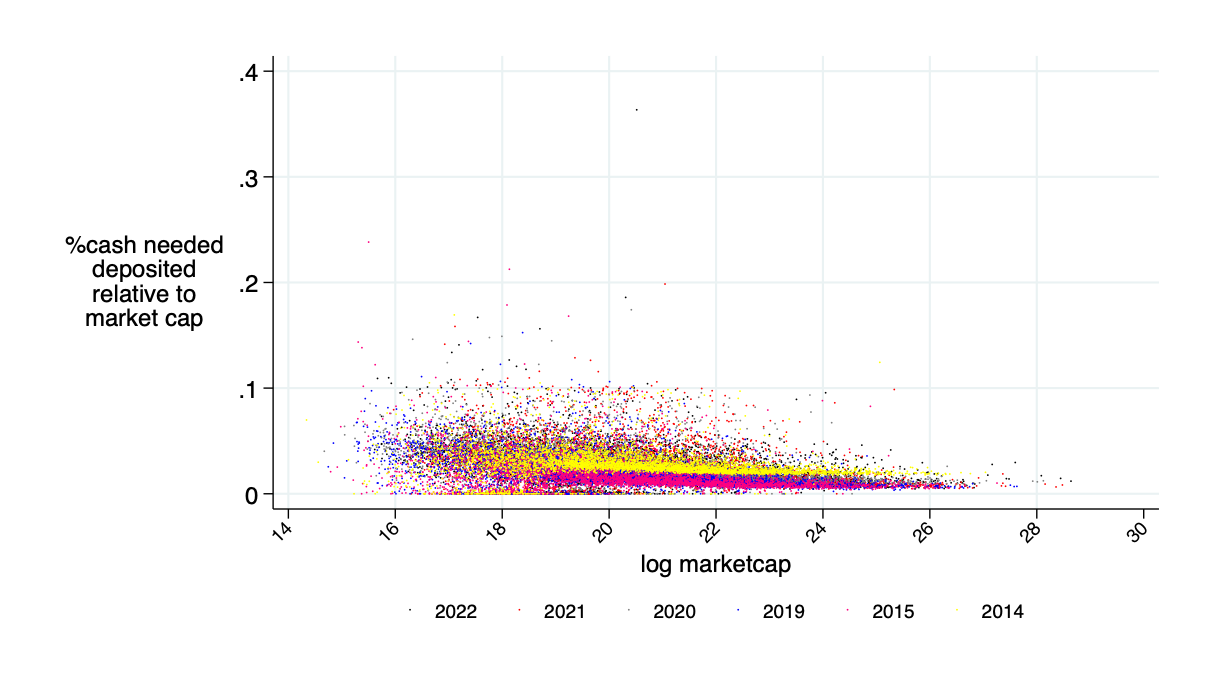
actually needed cash as fraction of "headline" amount

Only need about 5% of the 10% marketcap amount in cash

AMMs are better on about 85% of trading days

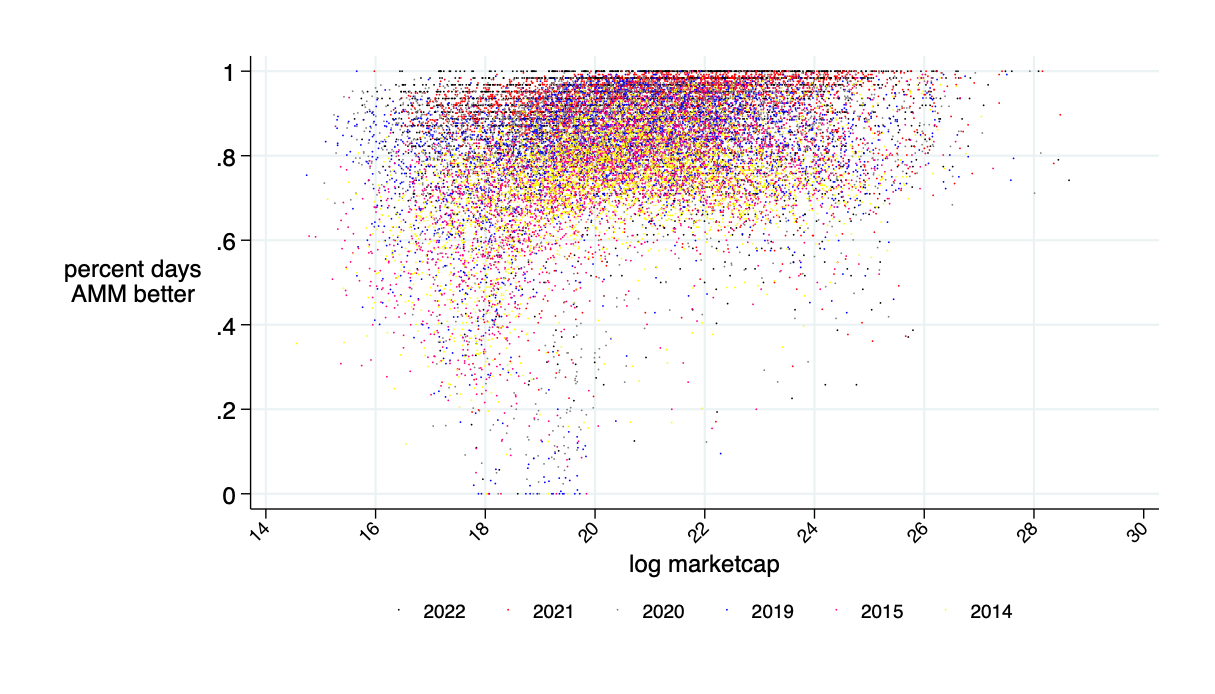
quoted spread minus AMM price impact minus AMM fee (all measured in bps)

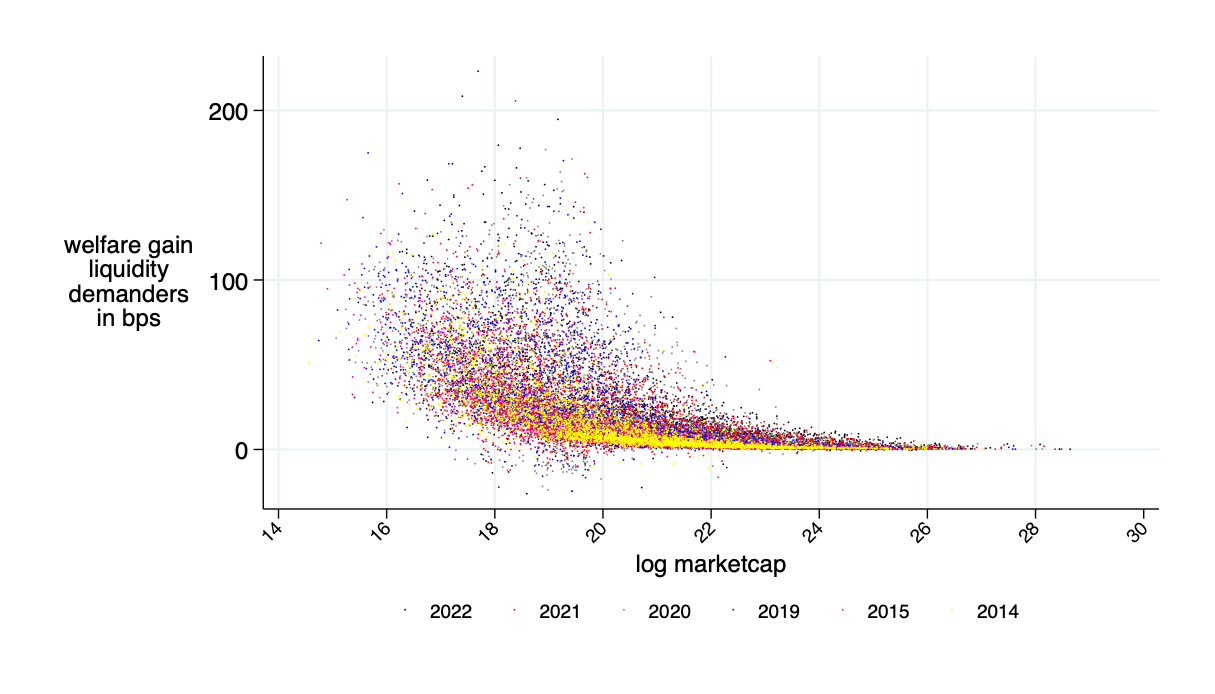
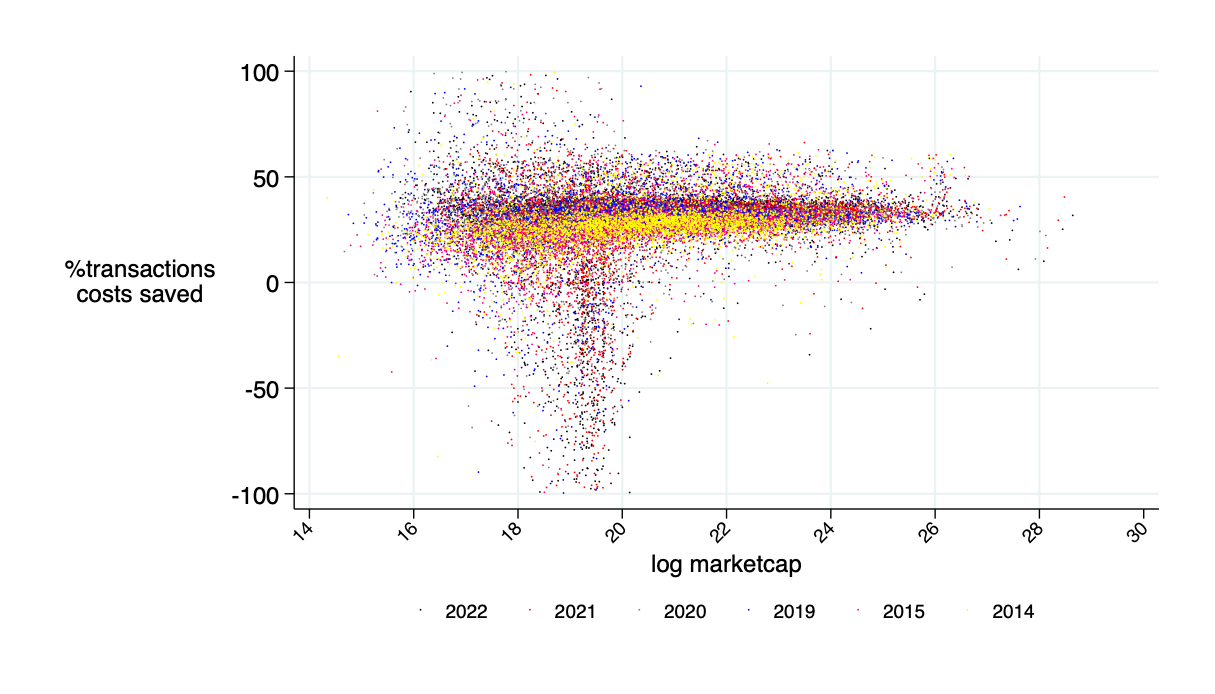
relative savings: what fraction of transactions costs would an AMM save? $\to$ about 30%

theoretical annual savings in transactions costs is about $15B

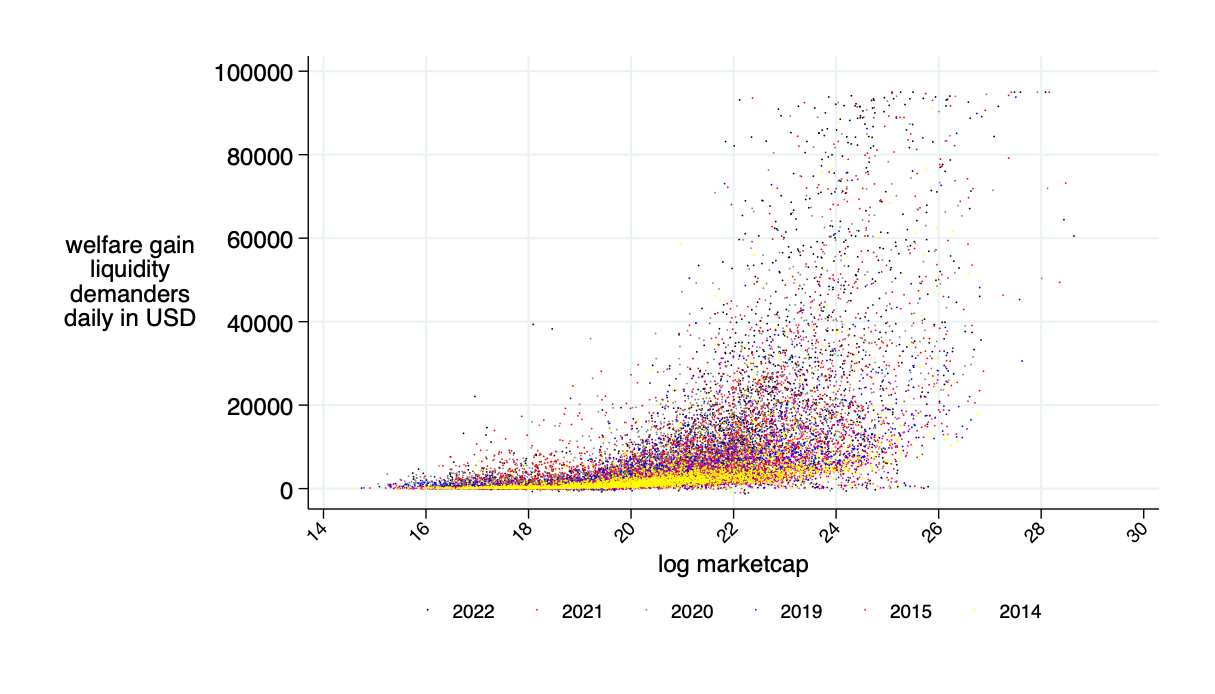
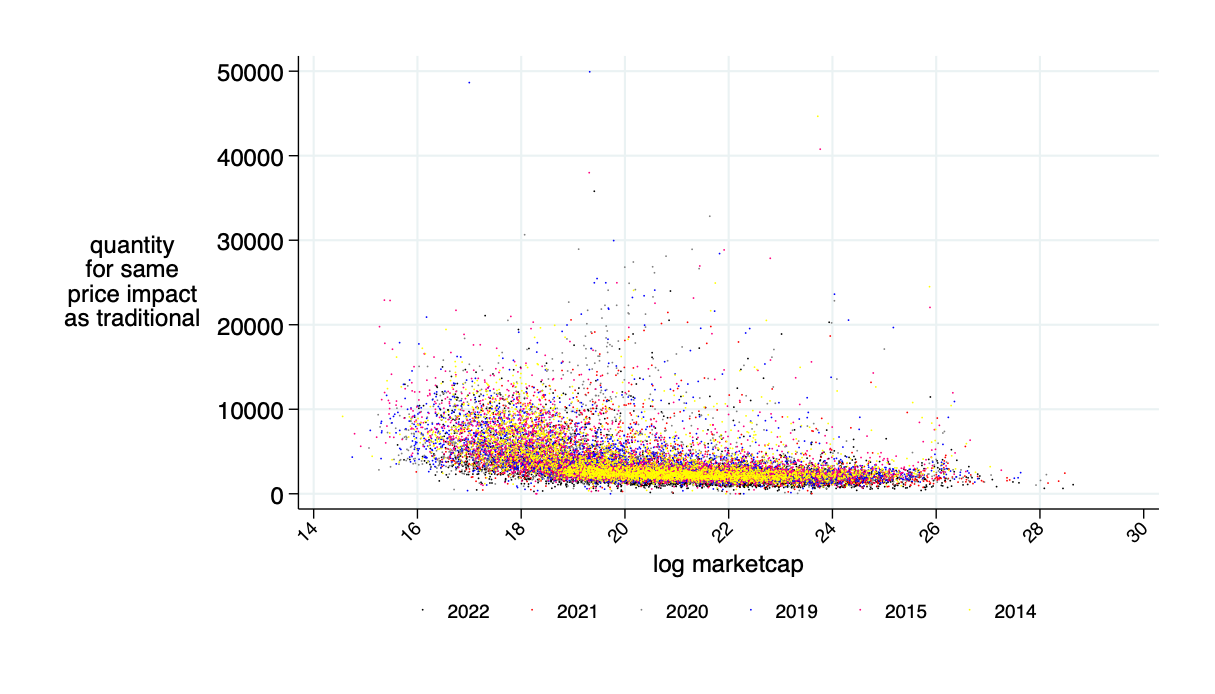
Sidebar: Capital Requirement

Deposit Requirements

Our approach: measure liquidity provision in % of market cap
Share-based liquidity provision is trivial: the shares are just sitting at brokerages.
But: requires an off-setting cash amount
Cash is not free:
- at 6% annual rate, must pay 2bps per day.
- Would need to add to fees
But: do we need "all that cash"?
No.

(hand-waving argument)
2nd gen AMMs have liquidity provision "bands": specify price range for which one supplies liquidity
Here: specify range for $R\in(\underline{R},\overline{R})$
Outside range: don't trade.
Inside range: "full" liquidity with constant product formula.
Implication: only need cash and shares to satisfy in-range liquidity demand.

For return $R$, the following number of shares change hands: \[q=a\cdot(1-\sqrt{R^{-1}}).\]
Fraction of share deposit used \[\frac{q}{a}=1-\sqrt{R^{-1}}.\]
Fraction of cash used \[\frac{\Delta c ("R")}{c}=\frac{1-\sqrt{R^{-1}}}{\sqrt{R^{-1}}}.\]
Example for $R=.9$ (max allowed price drop $=10\%$) \[\frac{\Delta c ("R")}{c}=-5\%.\]
$\Rightarrow$ "real" cash requirements $\not=$ deposits

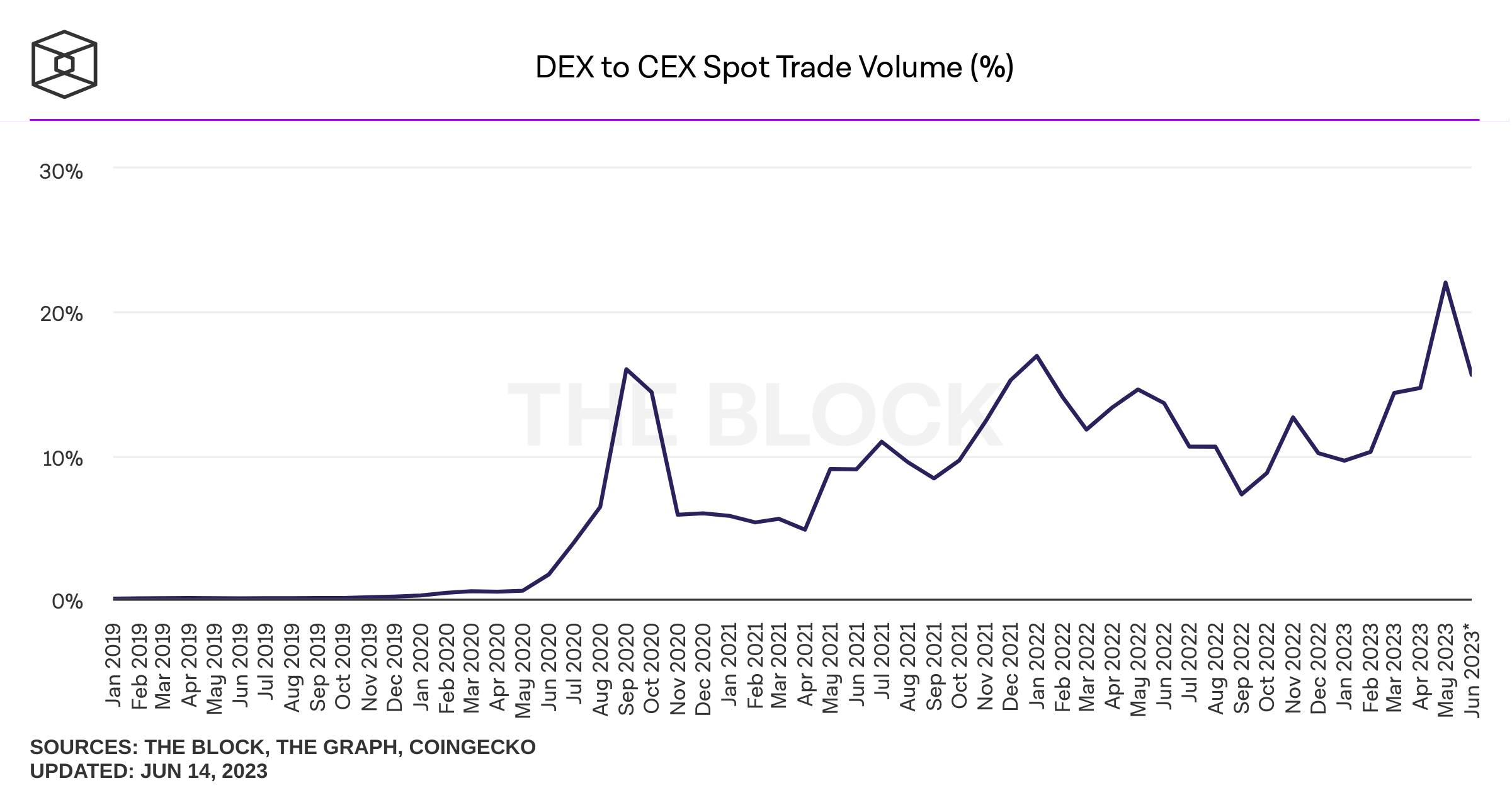
Literature

AMM Literature: a booming field

Theory
- Lehar and Parlour (2021): for many parametric configurations, investors prefer AMMs over the limit order market.
- Aoyagi and Ito (2021): co-existence of a centralized exchange and an automated market maker; informed traders react non-monotonically to changes in the risky asset’s volatility
- Capponi and Jia (2021): price volatility $\to$ welfare of AMM LPs; conditions for a breakdown of liquidity supply in the automated system; more convex pricing $\to$ lower arbitrage rents & less trading.
- Capponi, Jia, and Wang (2022): decision problems of validators, traders, and MEV bots under the Flashbots protocol.
- Park (2021): properties and conceptual challenges for AMM pricing functions
- Milionis, Moallemi, Roughgarden, and Zhang (2022): dynamic impermanent loss analysis for under constant product pricing.
- Hasbrouck, Rivera, and Saleh (2022): higher fee $\Rightarrow$ higher volume
Empirics:
- Lehar and Parlour (2021): price discovery better on AMMs
- Barbon and Ranaldo (2022): compare the liquidity CEX and DEX; argue that DEX prices are less efficient.
Math Literature: large number of papers that study AMMs in applied maths
- e.g. Cartea, Drissi, Monga (2023): closed form solution to IPL and optimizing strategy