Discussion of "Stablecoin Runs and the Centralization of Arbitrage"
Paper by Ma, Zeng, and Zhang
Discussion by: Andreas Park


What is a stablecoin?
digital representation of a unit of a fiat currency on a blockchain
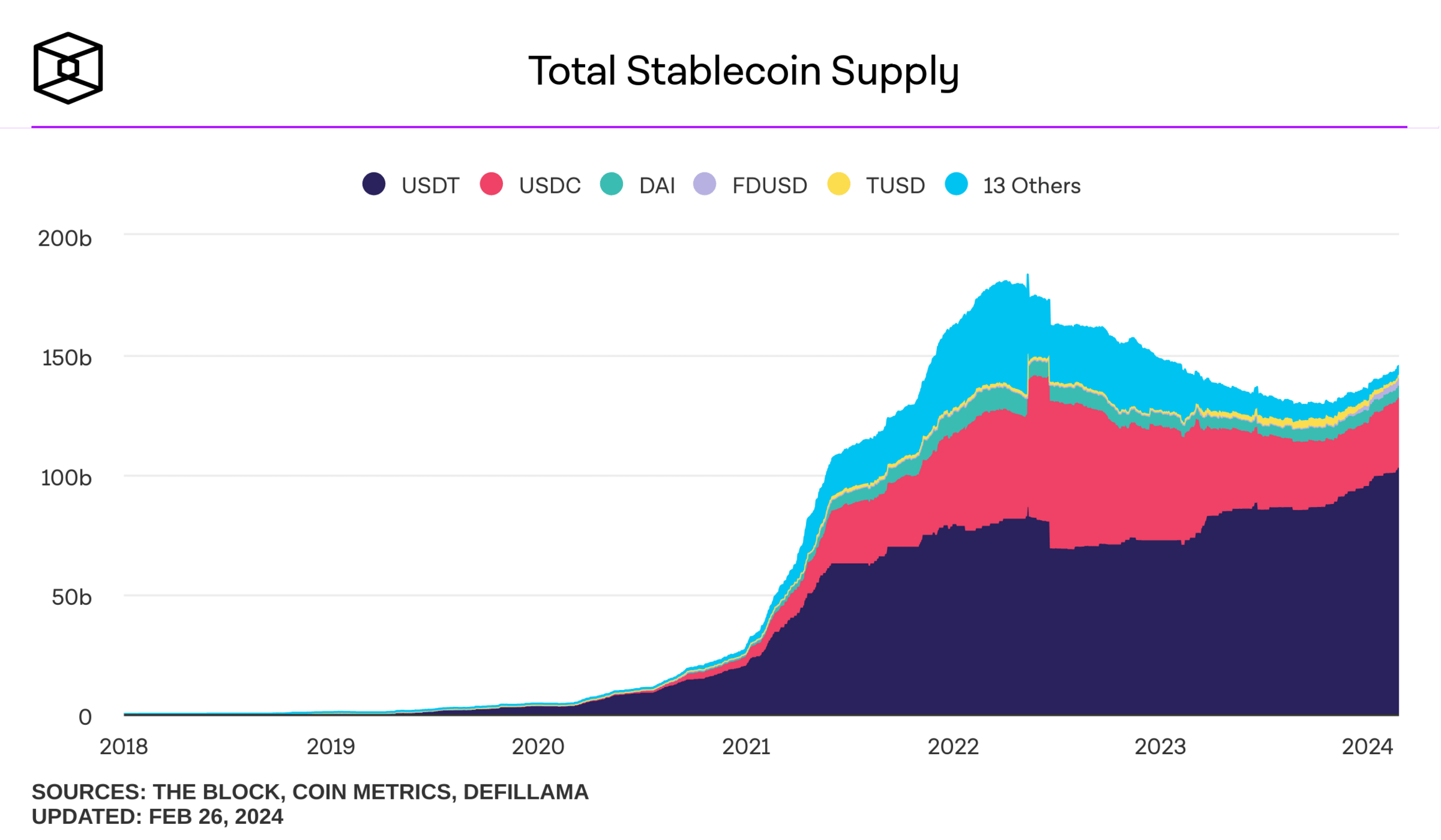
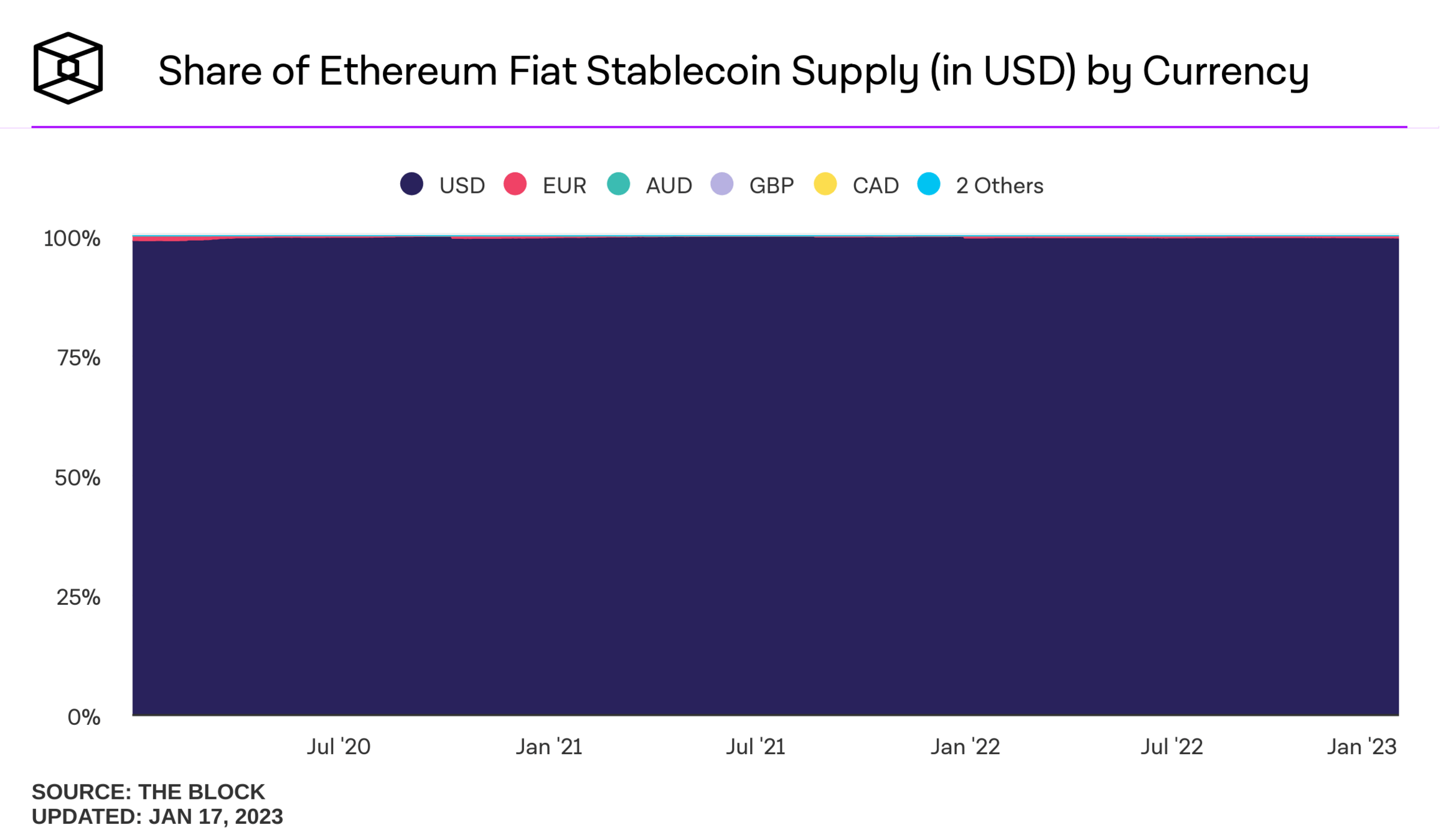
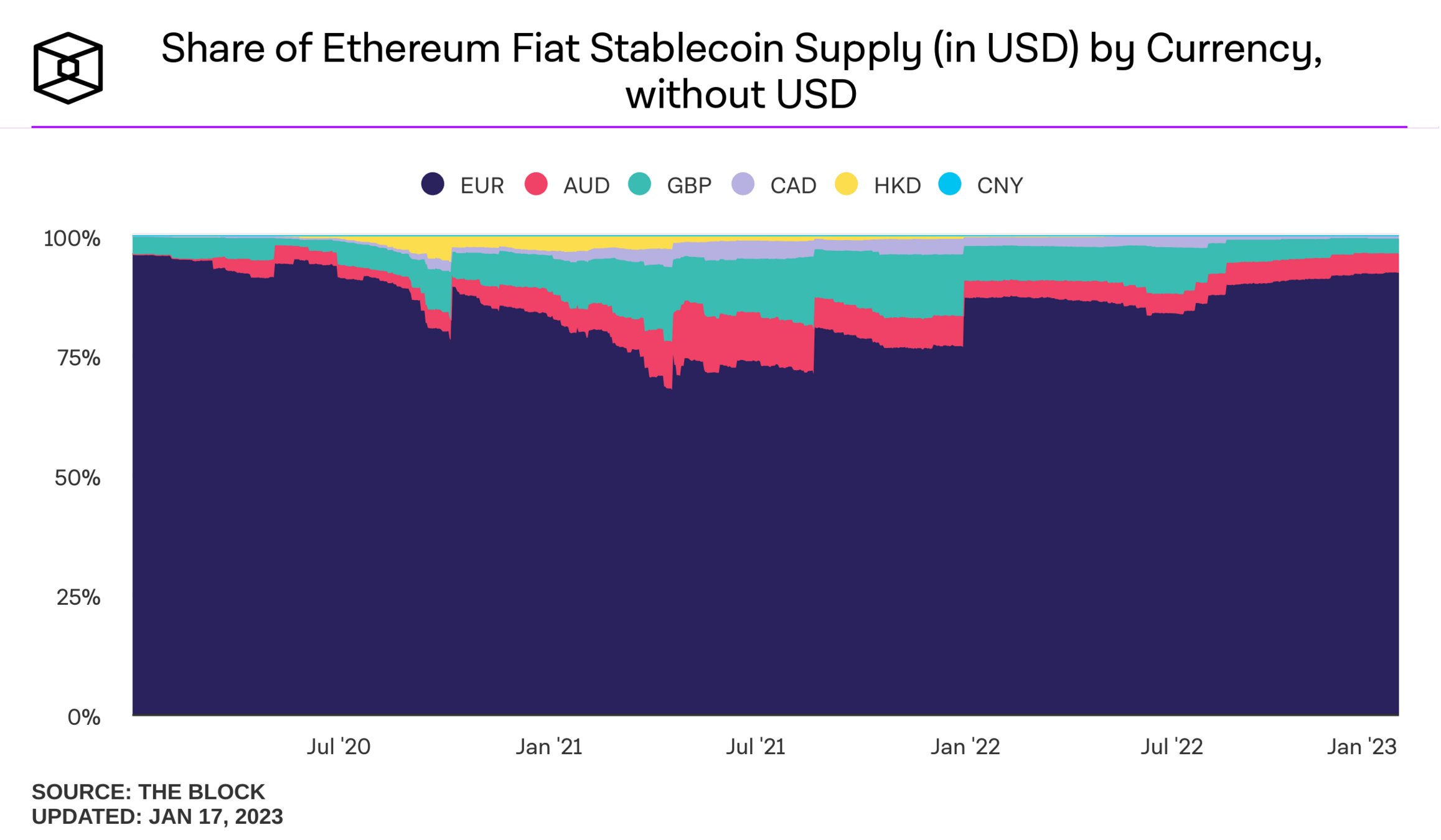
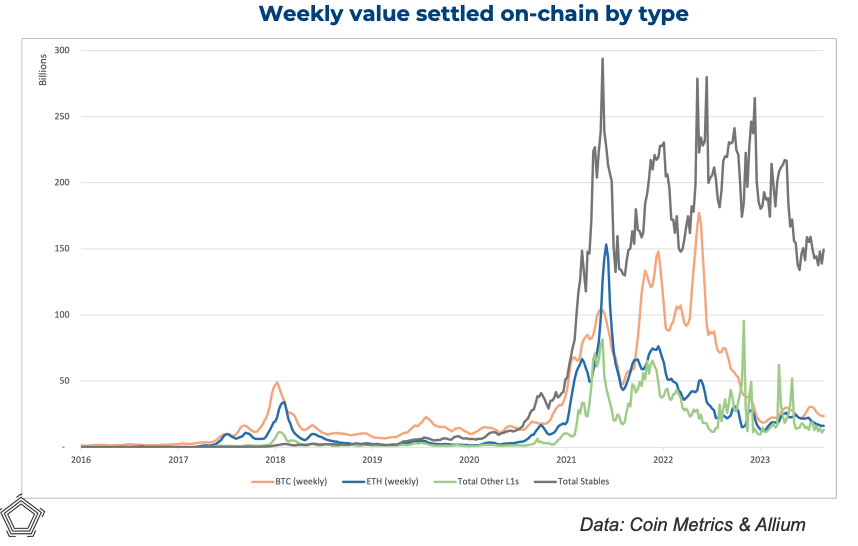
pulled from Nick Carter's talk on "Will stablecoins serve or subvert U.S. interests?"
stablecoins are crypto's/blockchain's first "killer" use case
BTC, ETH
HQLA: USD, EUR
asset (gold)
fee-backed
Seigniorage
Crypto
Traditional
Algorithmic
Collateral-Backed
Taxonomy of Stablecoins
DEPOSITS
other assets
JPM coin
USDC
USDT
UST, Basis, Neutrino
DAI, FEI
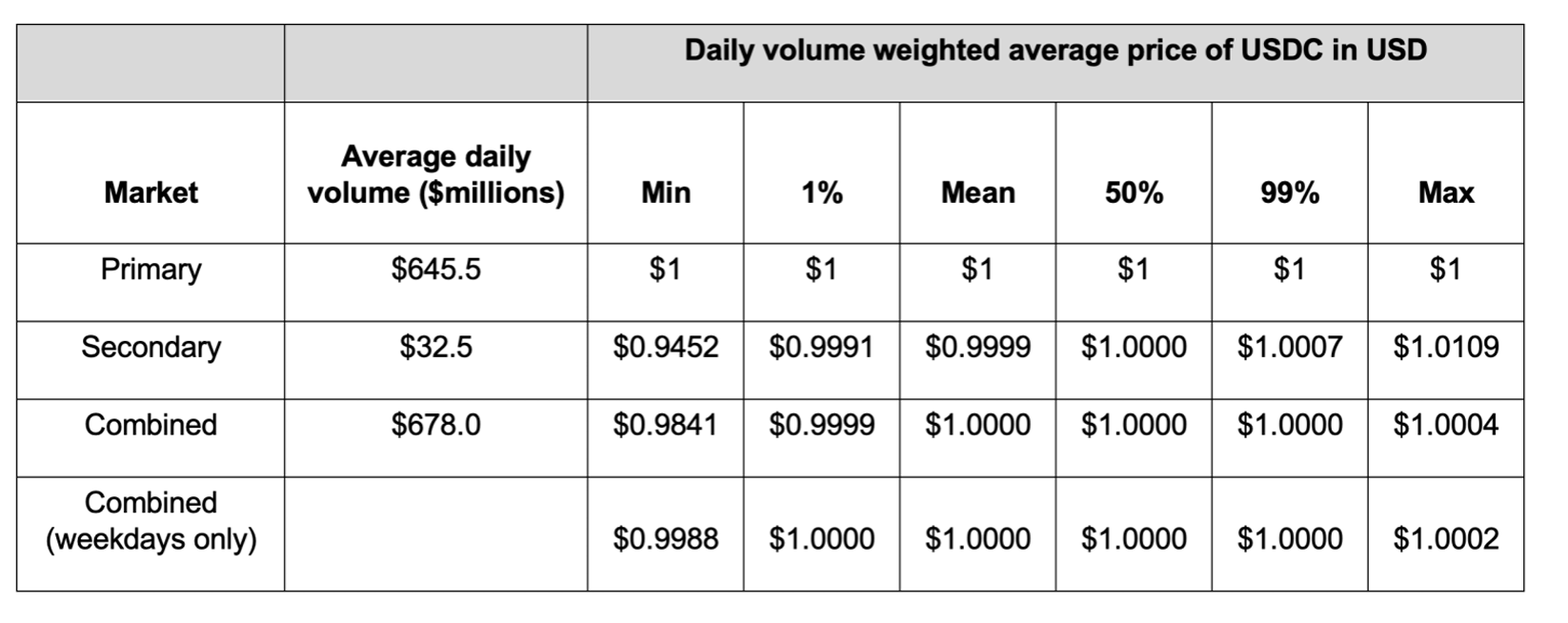
Collateral Backed Stablecoins: USDT & USDC





\(\Rightarrow\) 5% over-collateralized
primary market acces: 6 entities only
Collateral Backed Stablecoins: USDT & USDC

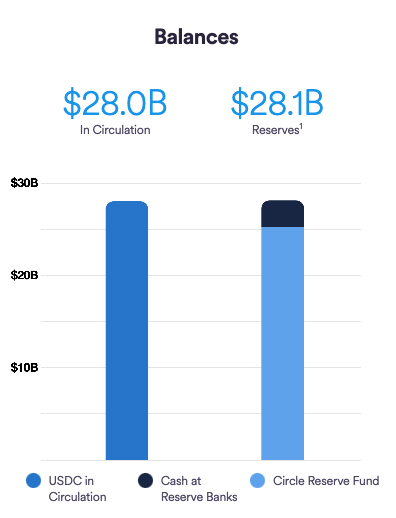
- "Cash at Reserve Banks" once was SVB
- Reserve fund = short-date US treasuries & overnight repos

primary market acces: 560+ entities
What makes a Stablecoin stable?
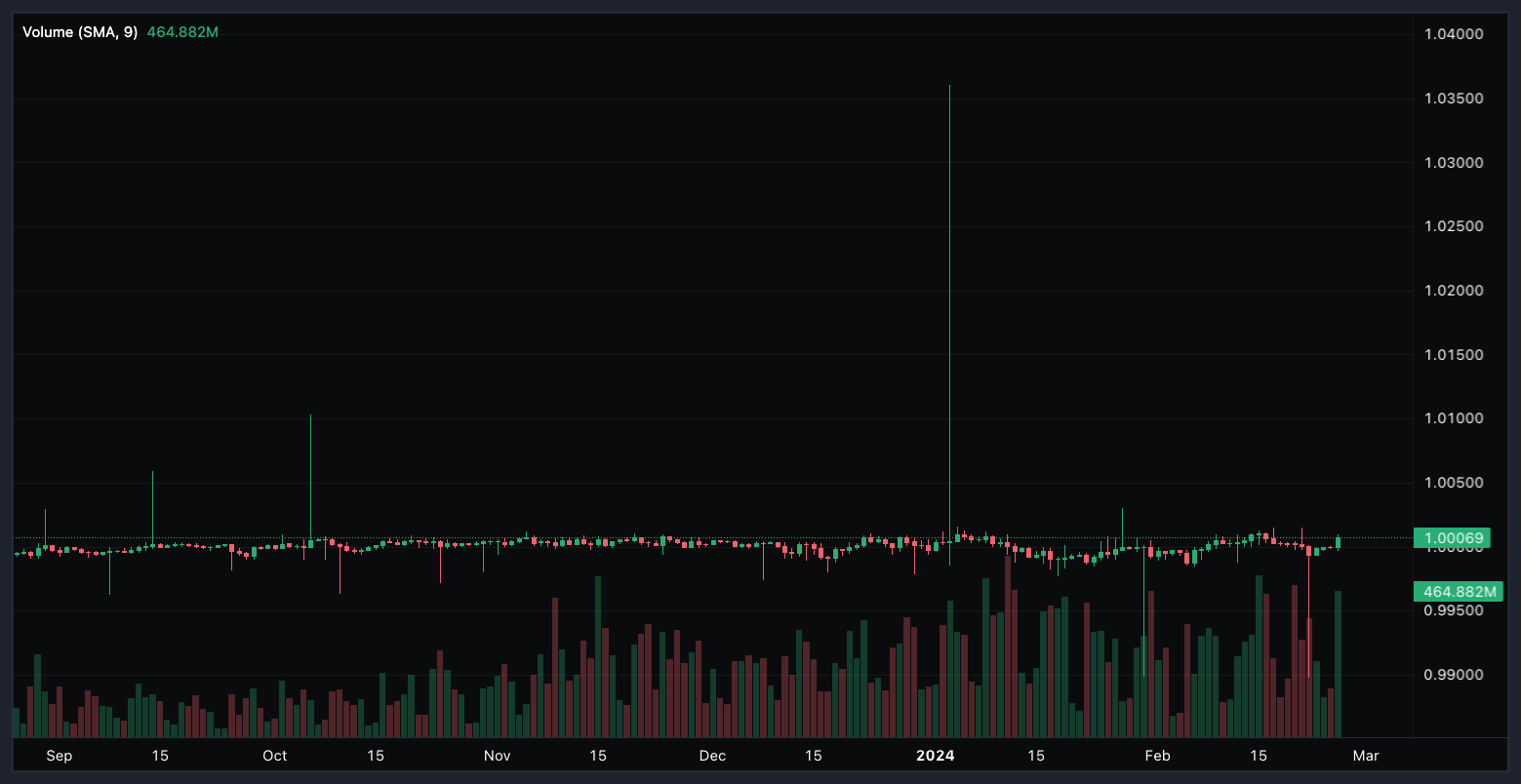
USD-USDT (6 months)
\(\Rightarrow\) need a primary/reference market mechanism to allow for forces of arbitrage to align prices
- stablecoins are issued
- by a single entity or
- a blockchain-based algorithm (smart contract)
- they trade in a secondary market
- on crypto-exchanges against fiat
- on crypto-exchanges against cryptos
- on-chain against other tokens
- \(\Rightarrow\) stablecoin price fluctuates
Arbitrage when price(stablecoin)>$1






arbitrageur
issuer/ primary market






secondary market


What makes a Stablecoin stable?
Arbitrage when price(stablecoin)<$1






arbitrageur
issuer/ primary market






secondary market


This paper: Runs!
Key Model Ingredients and what they do
1. stablecoin with primary and secondary market
2. liquidity transformation by stablecoin issuer \(\to\) Diamond-Dybvig bank run model
3. Morris-Shin-style global game
- secondary market trading creates price dislocations
- requires arbitrage related liquidations in the primary market
- arbitrage related primary market liquidations require early sale of illiquid asset
- prospect of early sale creates run risk
- primary assets subject to fundamental risk
- global games creates unique equilibrium for run
- run threshold is the key variable of interest
What's the Key Tension
- price drop stablecoin to USD prompts arbitrageurs to
- buy stablecoins for USD in secondary market
- sell stablecoins for USD at parity in primary market
-
to exchange stablecoins for USD at parity issuer needs to
-
find cash or
-
sell illiquid assets
-
Issues in the Secondary Market
Issues in the Primary Market
What's the Key Tension
What's the Key Mechanism
- running has costs
- you lose future convenience yield
- you sell when the price is below parity
- you have price impact
- (fire-)sale of illiquid assets is costly and reduces value of stablecoin backing
- highly illiquid backing makes costly sale more likely
- increases run risk
key implication:
less liquid backing \(\to\) more run risk
- price drop stablecoin to USD prompts arbitrageurs to
- buy stablecoins for USD in secondary market
- sell stablecoins for USD at parity in primary market
-
to exchange stablecoins for USD at parity issuer needs to
-
find cash or
-
sell illiquid assets
-
Issues in the Secondary Market
Issues in the Primary Market
key implication:
more liquidity \(\to\) more run risk
Intuition for Key Result
key implication:
more liquidity \(\to\) less price impact
less price impact \(\to\) more run risk
more abitrageurs \(\to\) more secondary market liquidity
Model Implications
- less liquid backing \(\to\) more run risk
- more arbitrageurs \(\to\) more run risk
- less liquid backing \(\to\) choose fewer arbitrageurs
- more liquid backing \(\to\) may have higher run risk (than expected)
Comments
Comment 0: all OK with the theory?
- theory model is fine (and well thought out)
- big question: is it true and does it capture what's going on?
Comment 1: What brings prices back to parity?
1. primary market arbitrage
2. secondary market arbitrage
Arbitrage when price(stablecoin)<$1






arbitrageur
issuer/ primary market






secondary market








arbitrageur
issuer/ primary market






secondary market










Cost on Kraken: .1 bps
Source: Liao (2023) "How to preserve the singleness of money for tokenised forms of money? "
Does secondary market activity justify primary market flows?
Comment 2: Price impact argument for infinitesimal investors
- secondary market liquidity does a lot of heavy lifting in the model
- concern about price impact is the cited reason for run aversion
- but: investors (prospective runners) are infinitesimal and have no price impact.
- So ... ?
Comment 3: cranky referee #2
censored ;-)
Comment 4: issuers optimize over #of arbitrageurs?
- key variable: # of arbitrageurs for primary market.
- Tether: 6
- Circle: 500+
- In the grand scheme of things, the choice of \(\phi\), the assets to back with seems much more salient.
- Appendix D is not convincing.
- alternative explanation: Tether has bad access to banking network
- \(\to\) cannot enable more arbitrageurs
Comments 5: odds and ends
- concentration measure for arbitrage
- fraction of top 5?
- why not Hirshman-Herfindahl Index (or 1/HHI)
-
institutions of Tether and Circle operations
-
Tether:
- large discrete chunks traditionally issued via Bitfinex
- banking connection in the Carribean \(\to\) cannot redeem for \(r\)
-
Circle:
- strong connection banking network
- high redeem-issuance frequency \(\to\) redeem USDC for \(r\)
-
Tether:
-
Calibration
- CDS spread \(\not=\) CDS price (since 2009), so Appendix G requires some work (see ISDA's pricing model or Augustin, Saleh, Xu (JEDC 2020))
Comment 3: cranky referee #2
- The formulation of theorems requires work.
-
Proposition 2: "The run threshold, that is, run risk, is increasing in \(\phi\) if and only if \(g(\phi) > K\), where \(g(\phi)\) is continuous and strictly decreasing in \(\phi\) , and satisfies \(\lim_{\phi \to 0} g(\phi)>0\)."
- Proposition 3: "When the stablecoin engages in a higher level of liquidity transformation, the stablecoin issuer optimally designs a more concentrated arbitrageur sector, that is, \(n\) decreases in \(\phi\) when \(\phi\) is not too large and the cumulative distribution function \(G\) is close to linear."
- same for other propositions
-
- comparative statics results are static but are described in text like they are dynamic