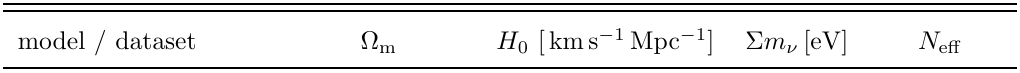DESI 2024: Survey Overview and Cosmological constraints from Baryon Acoustic Oscillations

Arnaud de Mattia

CEA Saclay

IRN, June 11th

Thanks to our sponsors and

72 Participating Institutions!

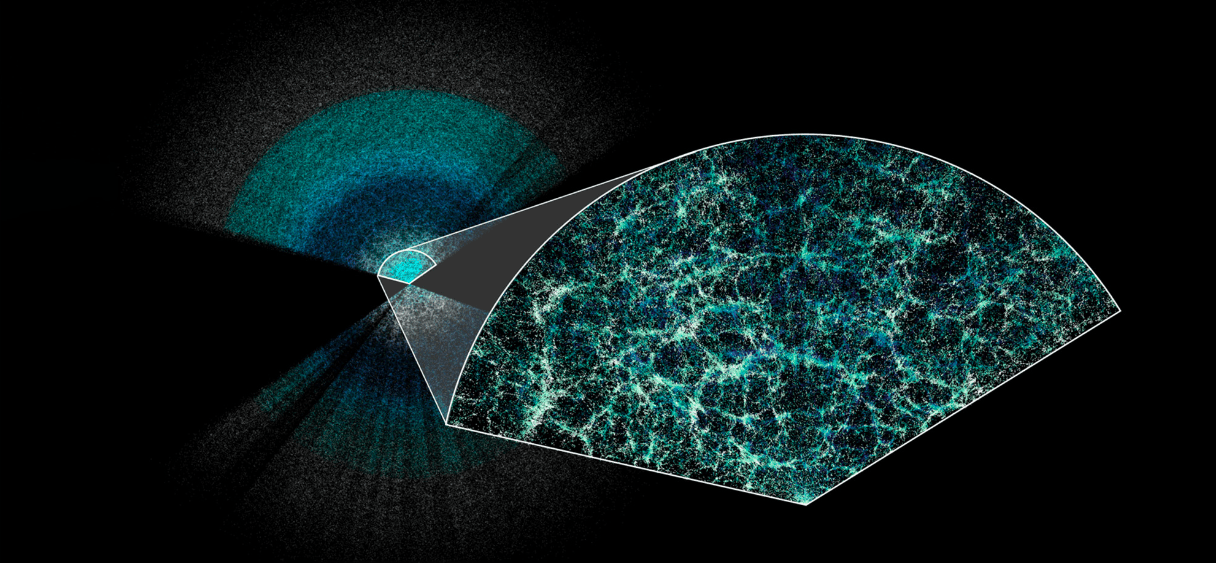
DESI 3D Map

Physics program
- Galaxy and quasar clustering
- Lyman-alpha forest
- Clusters and cross-correlations
- Galaxy and quasar physics
- Milky Way Survey
- Transients and low-z

DESI 3D Map

Physics program
- Galaxy and quasar clustering
- Lyman-alpha forest
- Clusters and cross-correlations
- Galaxy and quasar physics
- Milky Way Survey
- Transients and low-z

DESI Y5 galaxy samples

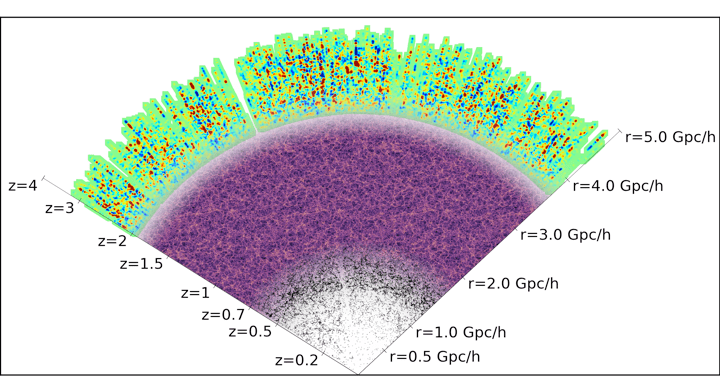
13.5 million Bright Galaxies

0 < z < 0.4

8 million LRGs

0.4 < z < 0.8

16 million ELGs

0.6 < z < 1.6

3 million QSOs

Lya \(1.8 < z\)

Tracers \(0.8 < z < 2.1\)

Y5 \(\sim 40\) M galaxy redshifts!

From images to redshifts

imaging surveys (2014 - 2019) + WISE (IR)

target selection

spectroscopic observations

spectra and redshift measurements

Mayall Telescope

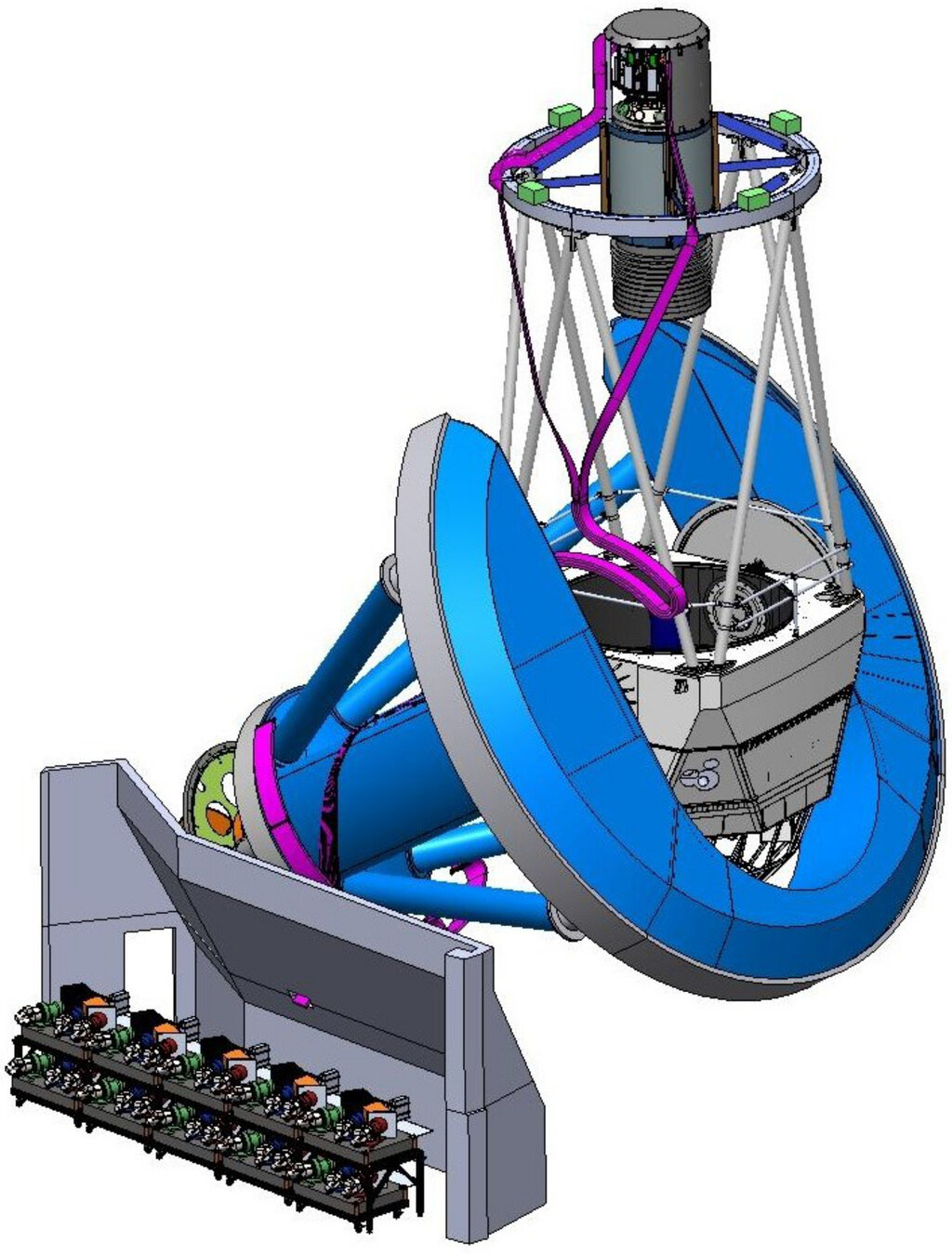
focal plane 5000 fibers

fiber view camera

wide-field corrector FoV \(\sim 8~\mathrm{deg}^{2}\)

ten 3-channel spectrographs

49 m, 10-cable fiber run

Kitt Peak, AZ

Focal plane: 5000 robotic positioners

86 cm

0.1 mm

Exposure time (dark): 1000 s

Configuration of the focal plane
CCD readout
Go to next pointing

140 s

Spectroscopic pipeline

wavelength

fiber number

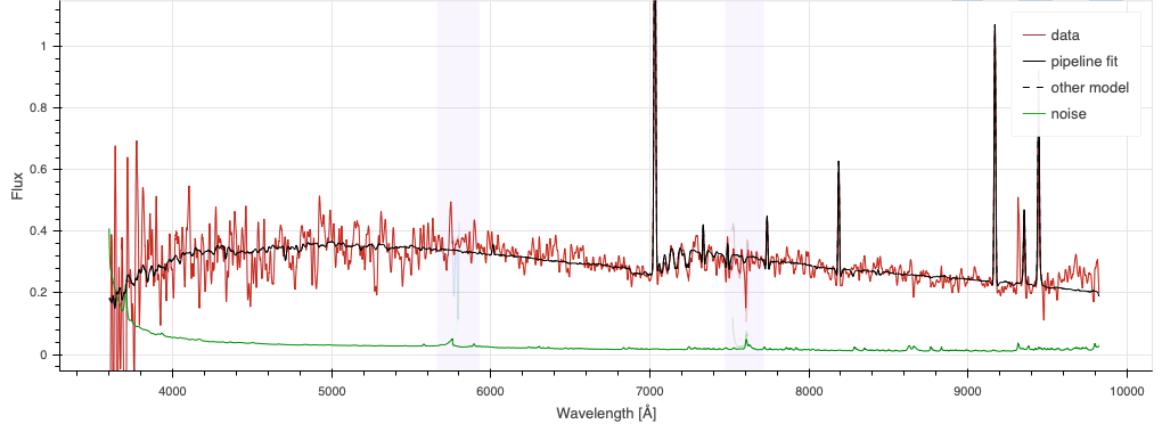
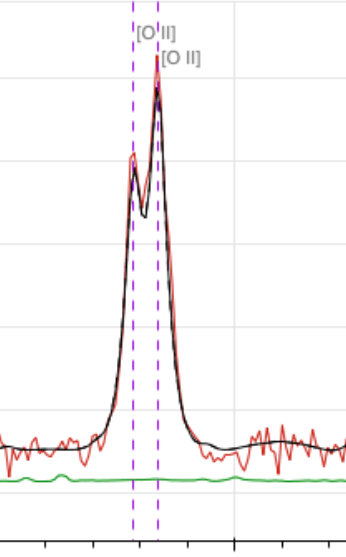
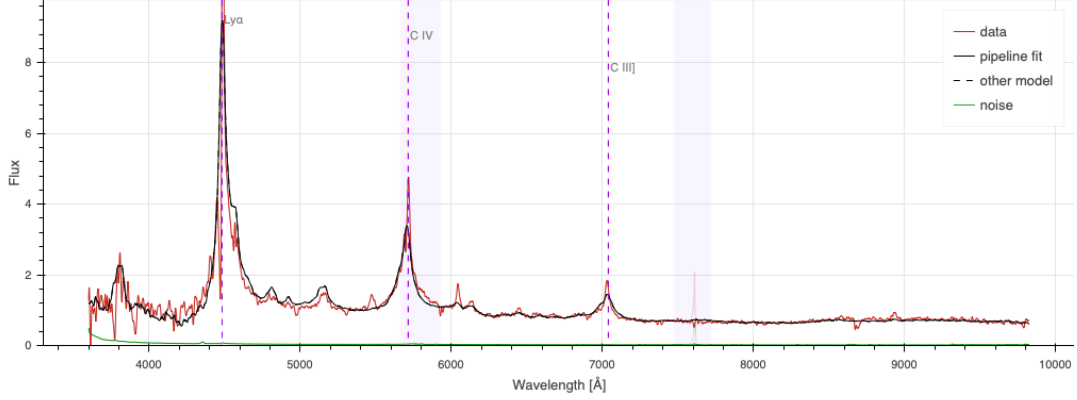
\(z = 2.1\) QSO

\(z = 0.9\) ELG

Ly\(\alpha\)

CIV

CIII

[OII] doublet at \(2727 \AA\) up to \(z = 1.6\)

[OII]

Ly\(\alpha\) at \(1216 \AA\) down to \(z = 2.0\)

DESI Y5 forecasts

Survey Validation (arXiv:2306.06307)

BAO and RSD constraints at the end of the survey (\( \Delta z = 0.1 \))

Ly\(\alpha\)

DESI Y5 forecasts

Survey Validation (arXiv:2306.06307)

BAO and RSD constraints at the end of the survey (\( \Delta z = 0.1 \))

Ly\(\alpha\)

(w/ Planck)

DESI data release 1 (DR1)

Observations from May 14th 2021 to June 12th 2022

Final survey

- dark time (LRG, ELG, QSO): 7 visits

- bright time (BGS): 5 visits

- 14,000 \(\mathrm{deg}^2\)

DESI data release 1 (DR1)

5.7 million unique redshifts at z < 2.1 and > 420,000 Ly\(\alpha\) QSO at z > 2.1

Release of DESI DR1 (BAO) results

April 4th 2024

First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/


• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements

Release of DESI DR1 (BAO) results

April 4th 2024

First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/


• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements

Baryon acoustic oscillations

Sound waves in primordial plasma

At recombination (\(z \sim 1100\))

  • plasma changes to optically thin
  • baryons decouple from photons
  • sound wave stalls

Baryon acoustic oscillations

Sound waves in primordial plasma

At recombination (\(z \sim 1100\))

  • plasma changes to optically thin
  • baryons decouple from photons
  • sound wave stalls

spherical shell in the distribution of galaxies, of radius the distance that sound waves travelled

= sound horizon scale at the drag epoch \( r_\mathrm{d} \sim 150 \; \mathrm{Mpc} \sim 100 \; \mathrm{Mpc}/h \)

  • transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
z
\theta_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{M}(z)

BAO measurements

transverse comoving distance

sound horizon \(r_d\)

  • transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
  • along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)

BAO measurements

z
\Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z)

Hubble distance

sound horizon \(r_d\)

  • transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
  • along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)

At multiple redshifts \(z\)

BAO measurements

z_1
z_2
z_3

Correlation functions

Excess probability to find 2 galaxies separated by a separation s

Correlation functions

BAO peak

Power spectra

Power spectra

BAO wiggles

Some fits: configuration space

isotropic measurement

anisotropic measurement

\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z)

Some fits: Fourier space

isotropic measurement

anisotropic measurement

\propto (D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}
\propto D_{\mathrm{M}}(z) / D_\mathrm{H}(z)

Non-linear evolution

Non-linear structure growth and peculiar velocities blur and shrink (slightly) the ruler

Eisenstein et al. 2008, Padmanabhan et al. 2012

Density field reconstruction

Estimates Zeldovich displacements from observed field and moves galaxies back: refurbishes the ruler (improves precision and accuracy)

reconstruction

Density field reconstruction

DESI DR1 BAO analysis

  • Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))

5.7 million unique redshifts

Effective volume \(V_\mathrm{eff} = 18 \; \mathrm{Gpc}^{3}\)

\(3 \times \) bigger than SDSS!

DESI DR1 BAO analysis

  • Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
  • Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
(\mathrm{R.A.}, \mathrm{Dec.}, z) \Longrightarrow (x, y, z) \Longrightarrow (\mathrm{R.A.}^\prime, \mathrm{Dec.}^\prime, z^\prime)

fiducial cosmology

blinded cosmology (\(\Omega_\mathrm{m}, w_0, w_a\))

(random & unknown)

DESI DR1 BAO analysis

  • Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
  • Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
(\mathrm{R.A.}, \mathrm{Dec.}, z) \Longrightarrow (x, y, z) \Longrightarrow (\mathrm{R.A.}^\prime, \mathrm{Dec.}^\prime, z^\prime)

fiducial cosmology

blinded cosmology (\(\Omega_\mathrm{m}, w_0, w_a\))

(random & unknown)

+ RSD blinding: change reconstructed peculiar velocities

+ \(f_\mathrm{NL}\) blinding: add clustering-dependent signal on large scales with weights

DESI DR1 BAO analysis

  • Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
  • Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
  • Theory developments in BAO fitting code
P_\mathrm{gg}(k, \mu) = \mathcal{B}(k, \mu) P_\mathrm{nw}(k) + \mathcal{C}(k, \mu) P_\mathrm{w}(k) + \orange{\mathcal{D}(k, \mu)}

Chen, Howlett et al. 2024

DESI DR1 BAO analysis

  • Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
  • Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
  • Theory developments in BAO fitting code
  • New and improved reconstruction methods
  • New combined tracer method used for overlapping galaxy samples (LRG and ELG in \(0.8 < z < 1.1\))

DESI DR1 BAO analysis

  • Biggest ever spectroscopic BAO dataset (\(N_\mathrm{tracer}\) and \(V\))
  • Blind analysis to mitigate observer / confirmation biases (catalog-level blinding)
  • Theory developments in BAO fitting code
  • New and improved reconstruction methods
  • New combined tracer method used for overlapping galaxy samples (LRG and ELG in \(0.8 < z < 1.1\))
  • Unified BAO pipeline applied to all (discrete) tracer / redshift bins consistently

Tests of systematic errors

Considered many possible sources of systematic errors using simulations and data:

  • observational effects (imaging systematics, fiber collisions)
  • BAO reconstruction (2 algorithms compared)
  • covariance matrix construction
  • incomplete theory modelling
  • choice of fiducial cosmology
  • galaxy-halo (HOD) model uncertainties

no systematics detected

systematics << statistics

Max effect: \(\sigma_\mathrm{stat. + syst.} < 1.05 \sigma_\mathrm{stat.}\)

Release of DESI DR1 (BAO) results

April 4th 2024

First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/


• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements

Ly\(\alpha\) forest

Absorption in QSO spectra by neutral hydrogen in the intergalactic medium: \(\lambda_\mathrm{abs} = (1 + z_\mathrm{HI}) \times 1215.17 \; \AA \)

Transmitted flux fraction \(F = e^{-\tau}\) probes the fluctuation in neutral hydrogen density, \(\tau \propto n_\mathrm{HI} \)

credit: Andrew Pontzen

Ly\(\alpha\) correlation functions in DESI DR1

Ly\(\alpha\) - Ly\(\alpha\)

Ly\(\alpha\) - QSO

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))

>420,000 Ly\(\alpha\) QSO at z > 2.1

\(2 \times \) more than SDSS!

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
  • Modelling of the correlation function:
    • cosmo signal
P_{\mathrm{Ly}\alpha}(k, \mu) = \blue{b^{2} (1 + \beta \mu^2)^2} \orange{P_\mathrm{lin}(k, \mu)} \green{F_\mathrm{NL}(k, \mu)}

linear bias + RSD

hydro-sim

BAO

\mu = r_\parallel / \sqrt{r_\parallel^2 + r_\perp^2}

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
  • Modelling of the correlation function:
    • cosmo signal
    • high-column density
    • metal absorbers
r_\parallel \propto \left\vert\frac{1}{\lambda_{\mathrm{Ly}\alpha}} - \frac{1}{\lambda_{\mathrm{metal}}}\right\vert

SiII

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
  • Modelling of the correlation function:
    • cosmo signal
    • high-column density
    • metal absorbers
    • correlated noise (sky subtraction)

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
  • Modelling of the correlation function

physical model fit

+ broadband polynomial

 

broadband: \(< 0.1\sigma\)

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
  • Modelling of the correlation function
  • Cross-covariance matrix

Correlation matrix

smoothed jackknife, validated with mocks

10% impact on BAO uncertainty

DESI DR1 Ly\(\alpha\) BAO analysis

  • Biggest ever Ly\(\alpha\) dataset (\(N_\mathrm{tracer}\))
  • First blind analysis to mitigate observer / confirmation biases (correlation function-level blinding)
  • Modelling of the correlation function
  • Cross-covariance matrix
  • Very stable results, systematic uncertainty neglected

Tests of systematic errors

tests with same dataset (not red): shifts \(< \sigma_\mathrm{stat}/3\)

tests with varying datasets (red): shifts consistent with stat.

Release of DESI DR1 (BAO) results

April 4th 2024

First batch of DESI DR1 cosmological analyses
https://data.desi.lbl.gov/doc/papers/


• DESI 2024 I: First year data release
• DESI 2024 II: DR1 catalogs
• DESI 2024 III: BAO from Galaxies and Quasars
• DESI 2024 IV: BAO from the Lyman-Forest
• DESI 2024 V: RSD from Galaxies and Quasars
• DESI 2024 VI: Cosmological constraints from BAO measurements
• DESI 2024 VII: Cosmological constraints from RSD measurements

  • transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
  • along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)
  • low S/N, isotropic average: \( D_\mathrm{V}(z) / r_\mathrm{d} = (z D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}\)

BAO measurements

BAO measures ratios of distances over the sound horizon scale at the drag epoch ["standard ruler"] \(r_\mathrm{d}\)

Let's factor out the \(h\) terms:

  • ​\(\color{blue}{[D_\mathrm{M}(z) h] (\Omega_\mathrm{m}, f_\mathrm{DE}, \Omega_\mathrm{K}, ...)} \color{black}{/} \color{orange}{[r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h]} \)
  • \( \color{blue}{[D_\mathrm{H}(z) h] (\Omega_\mathrm{m}, f_\mathrm{DE}, \Omega_\mathrm{K}, ...)} \color{black}{/} \color{orange}{[r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h]} \)

BAO measurements at different \(z\) constrain:

  • energy content \( \color{blue}{(\Omega_\mathrm{m}, f_\mathrm{DE}, ...)} \)
  • constant-over-\(z\) product \(\color{orange}{r_\mathrm{d} h}\) i.e. \(\color{orange}{H_{0} r_\mathrm{d}}\)

These quantities directly relate to base cosmological parameters

BAO measurements

\(h = H_{0} / [100\; \mathrm{km}/\mathrm{s} / \mathrm{Mpc}]\)

\(\Omega_\mathrm{m}\) fractional energy density of matter

\(f_\mathrm{DE}\) dark energy

\(\Omega_\mathrm{K}\) curvature

\(\Omega_{b}\) baryons

DESI Y1 BAO

DESI BAO measurements

DESI Y1 BAO

DESI BAO measurements

DESI Y1 BAO

DESI BAO measurements

DESI Y1 BAO

DESI BAO measurements

DESI Y1 BAO

DESI BAO measurements

DESI Y1 BAO

DESI BAO measurements

DESI Y1 BAO

DESI BAO measurements

Consistent with each other,

and complementary

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.295 \pm 0.015 & \mathbf{(5.1\%)} \\ H_{0} r_\mathrm{d} &= (101.8 \pm 1.3) \, [100 \, \mathrm{km} \, \mathrm{s}^{-1}] & \mathbf{(1.3\%)} \end{align*}}_{\textstyle \text{\color{black}{DESI}}}

Consistency with other probes

DESI Y1 BAO consistent with:

Consistency with other probes

DESI Y1 BAO consistent with:

Consistency with other probes

DESI Y1 BAO consistent with:

Consistency with other probes

DESI Y1 BAO consistent with:

\underbrace{ \Omega_\mathrm{m} = 0.3069 \pm 0.0050 \; \mathbf{(1.6\%)} }_{\textstyle \text{\green{DESI + CMB}}}
  • BAO constrains \( r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h \)

Hubble constant

  • BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \Omega_\mathrm{b} h^{2}) h \)
  • \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)

Hubble constant

  • BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \orange{\Omega_\mathrm{b} h^{2}}) h \)
  • \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
  • \(\orange{\Omega_\mathrm{b}h^2}\) can be constrained by light element abundance from Big Bang Nucleosynthesis (BBN): Schöneberg et al., 2024

Hubble constant

  • BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \orange{\Omega_\mathrm{b} h^{2}}) h \)
  • \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
  • \(\orange{\Omega_\mathrm{b}h^2}\) can be constrained by light element abundance from Big Bang Nucleosynthesis (BBN): Schöneberg et al., 2024

\(\implies\) constraints on \(h\) i.e. \(H_0 = 100 h \; \mathrm{km} / \mathrm{s} / \mathrm{Mpc}\)

Hubble constant

\underbrace{ H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}

Hubble constant

\underbrace{ H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}

\(\theta_\ast\) CMB angular acoustic scale

 

​

 

  • Consistency with SDSS
\underbrace{ H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}

Hubble constant

\underbrace{ H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}

 

​

 

  • Consistency with SDSS
  • In agreement with CMB
\underbrace{ H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}

Hubble constant

\underbrace{ H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}

 

​

 

  • Consistency with SDSS
  • In agreement with CMB
  • In \(3.7 \sigma\) tension with SH0ES
\underbrace{ H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}

Hubble constant

\underbrace{ H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}} }_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}

DESI + CMB measurements favor a flat Universe

\Omega_\mathrm{K} = 0.0024 \pm 0.0016 \; \green{(\text{DESI} + \text{CMB})}

Spatial curvature

Dark Energy Equation of State

Dark Energy fluid, pressure \(p\), density \(\rho\)

Equation of State parameter \(w = p / \rho\)

Linked to the evolution of Dark Energy \(w(z) = -1 + \frac{1}{3}\frac{d \ln f_\mathrm{DE}(z)}{d \ln (1 + z)}\)

Dark Energy Equation of State

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\ w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)} \end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}

Constant EoS parameter \(w = p / \rho\)

\Lambda

Dark Energy Equation of State

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\ w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)} \end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}

Constant EoS parameter \(w = p / \rho\)

Dark Energy Equation of State

SNe:

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\ w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)} \end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}

Constant EoS parameter \(w = p / \rho\)

Dark Energy Equation of State

SNe:

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\ w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)} \end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}

Constant EoS parameter \(w = p / \rho\)

Dark Energy Equation of State

SNe:

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\ w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)} \end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}

Constant EoS parameter \(w = p / \rho\)

Dark Energy Equation of State

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.3095 \pm 0.0065 & \mathbf{(2.1\%)} \\ w &= -0.997 \pm 0.025 & \mathbf{(2.5\%)} \end{align*}}_{\textstyle \text{\color{orange}{DESI + CMB + Pantheon+}}}

Assuming a constant EoS, DESI BAO fully compatible with a cosmological constant...

\underbrace{\begin{align*} \Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\ w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)} \end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}

Constant EoS parameter \(w = p / \rho\)

w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}
\left. \begin{align*} w_{0} &= -0.55^{+0.39}_{-0.21} \\ w_{a} &< -1.32 \end{align*} \right\rbrace {\text{\color{black}{DESI}}}

Dark Energy Equation of State

Varying EoS

\Lambda

Dark Energy Equation of State

\underbrace{ w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00} }_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}

Varying EoS

w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}

Dark Energy Equation of State

\underbrace{ w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00} }_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}

Varying EoS

w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}

Dark Energy Equation of State

\underbrace{ w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00} }_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}

Varying EoS

w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}

Dark Energy Equation of State

\underbrace{ w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00} }_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}

Varying EoS

w(z) = w_{0} + \frac{z}{1 + z} w_{a} \qquad \text{(CPL)}

Dark Energy Equation of State

Combining all DESI + CMB + SN

\underbrace{ w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25} }_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}

Dark Energy Equation of State

Combining all DESI + CMB + SN

\underbrace{ w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25} }_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{ w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34} }_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}

Dark Energy Equation of State

Combining all DESI + CMB + SN

\underbrace{ w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25} }_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{ w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34} }_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
\underbrace{ w_{0} = -0.727 \pm 0.067 \qquad w_{a} = -1.05^{+0.31}_{-0.27} }_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 3.9\sigma}}

Dark Energy Equation of State

Combining all DESI + CMB + SN

\(w_{0} > -1, w_{a} < 0\) favored, level varying on the SN dataset

\underbrace{ w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25} }_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{ w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34} }_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
\underbrace{ w_{0} = -0.727 \pm 0.067 \qquad w_{a} = -1.05^{+0.31}_{-0.27} }_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 3.9\sigma}}

Sum of neutrino masses

Internal CMB degeneracies limiting precision on the sum of neutrino masses

Sum of neutrino masses

Internal CMB degeneracies limiting precision on the sum of neutrino masses

Broken by BAO, especially through \(H_{0}\)

Low preferred value of \(H_{0}\) yields

\(\sum m_\nu < 0.072 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}\)

Limit relaxed for extensions to \(\Lambda\mathrm{CDM}\)

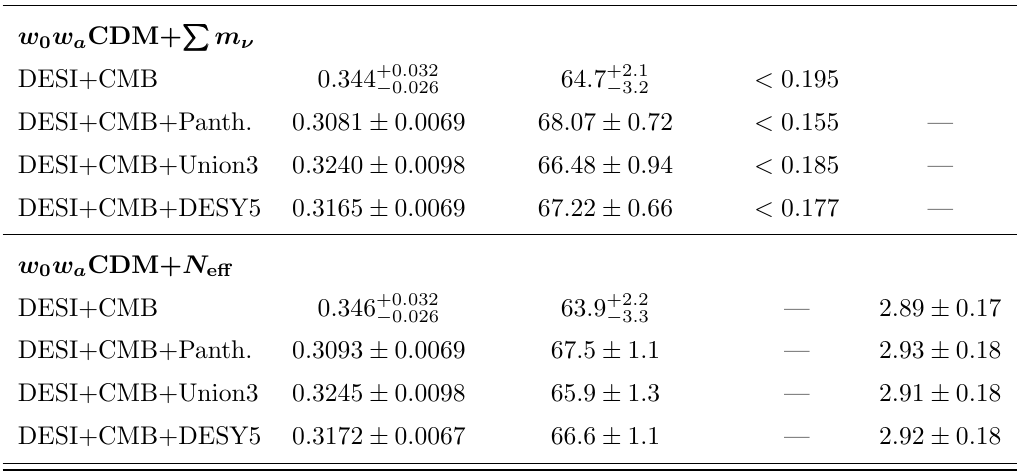
\(\sum m_\nu < 0.195 \, \mathrm{eV}\) for \(w_0w_a\mathrm{CDM}\)

Neutrino mass hierarchies

\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}

With \(> 0.059 \, \mathrm{eV}\) prior (NH)

Neutrino mass hierarchies

\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
\sum m_\nu < 0.145 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}

With \(> 0.059 \, \mathrm{eV}\) prior (NH)

With \(> 0.1 \, \mathrm{eV}\) prior (IH)

Neutrino mass hierarchies

\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
\sum m_\nu < 0.145 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}

With \(> 0.059 \, \mathrm{eV}\) prior (NH)

With \(> 0.1 \, \mathrm{eV}\) prior (IH)

Current constraints do not strongly favor normal over inverted hierarchy (\(\simeq 2 \sigma\))

Summary

DESI already has the most precise BAO measurements ever

Summary

DESI already has the most precise BAO measurements ever

 

DESI BAO is consistent (at the \(\sim 1.9\sigma\) level) with CMB in flat ΛCDM

Summary

DESI already has the most precise BAO measurements ever

 

DESI BAO is consistent (at the \(\sim 1.9\sigma\) level) with CMB in flat ΛCDM

 

In flat ΛCDM, DESI prefers "small \(\Omega_\mathrm{m}\), large \(H_0\) (though \(3.7\sigma\) away from SH0ES), small \(\sum m_\nu\)"

Summary

DESI already has the most precise BAO measurements ever

 

DESI BAO is consistent (at the \(\sim 1.9\sigma\) level) with CMB in flat ΛCDM

 

In flat ΛCDM, DESI prefers "small \(\Omega_\mathrm{m}\), large \(H_0\) (though \(3.7\sigma\) away from SH0ES), small \(\sum m_\nu\)"

 

Some hint of time-varying Dark Energy equation of state especially when combined with supernovae measurements

What's next?

"Full shape" (not only BAO peak measurement) analysis

 

Y3 data on disk!

The Pipeline

All codes public

The Pipeline

All codes public

desilike

- BAO, full shape likelihoods, designed to extend to other observables (lensing, etc.)

- wraps PT codes: velocileptors, pybird, folps(ax)

- automated cobaya / cosmosis / montepython bindings

- wraps samplers, profilers, fisher, in-place emulation

- "JAXification"

template = DirectPowerSpectrumTemplate(z=1.)
theory = LPTVelocileptorsTracerPowerSpectrumMultipoles(ells=(0, 2, 4), template=template)
theory(h=0.7, b1p=1.2)  # returns pk
observable = TracerPowerSpectrumMultipoles(data=data, wmatrix=wmatrix, theory=theory,
										   klim={0: (0.02, 0.2), 2: (0.02, 0.2)})
likelihood = ObservablesGaussianLikelihood(observables=observable)
likelihood(Omega_m=0.3)  # returns log-posterior

Other datasets

\(\sum m_\nu\)

credit: Christophe Yèche

\(w(z)\)

DESI - SDSS consistency (\(\Omega_\mathrm{m}\))

Perfectly consistent!

Using these 2 points alone moves \(\Omega_\mathrm{m}\) by \(< 2 \sigma\)

Are SN \(\Omega_\mathrm{m}\) consistent?

Not so much in flat \(\Lambda\mathrm{CDM}\)...

(so we do not combine them in this model!)

Are SN \(\Omega_\mathrm{m}\) consistent?

Consistent in \(w_0w_a\mathrm{CDM}\)!

plik vs PR4 Planck likelihoods

Appendix B

\(w_0 - w_a\) with \(\sum m_\nu\) free

\(w_0 - w_a\) with \(\Omega_\mathrm{K}\)

Preference for \(w_{0} > -1, w_{a} < 0\) persists when curvature is left free

DE constraints driven by low-\(z\) ?

Not that much!

 

DESI + SDSS swaps DESI measurements with SDSS for \(z < 0.6\)

 

\(- 0.4 \sigma\) compared to DESI only

\(w(z)\)

Dark energy equation of state:

\(P = w \rho\)

  • \(w\) = constant

BAO measurements: dark energy

Dark energy equation of state:

\(P = w \rho\)

  • CPL parameterization: \(w(a) = w_0 + (1 - a) w_a\)

BAO measurements: dark energy

Full tables

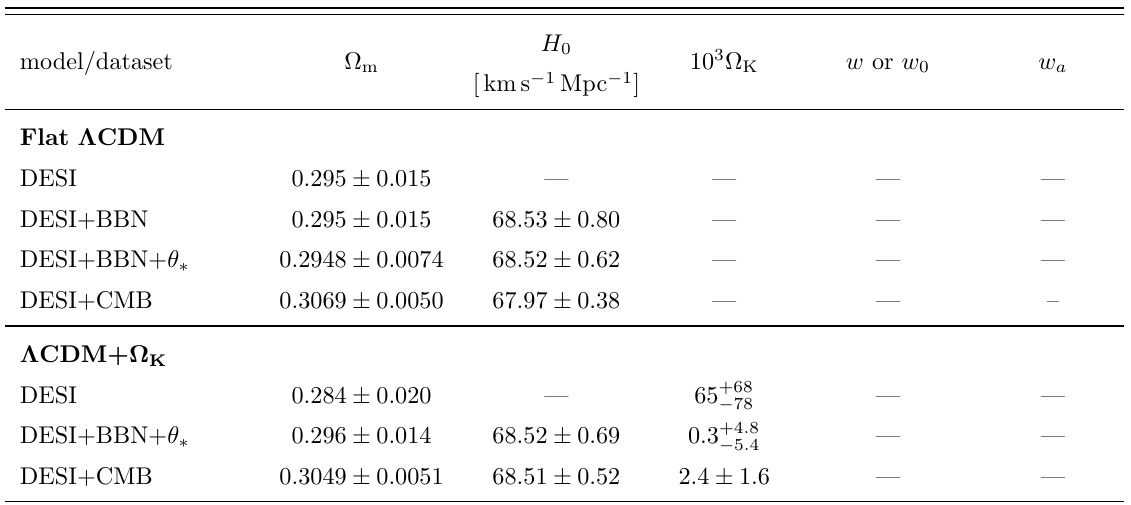
Full tables

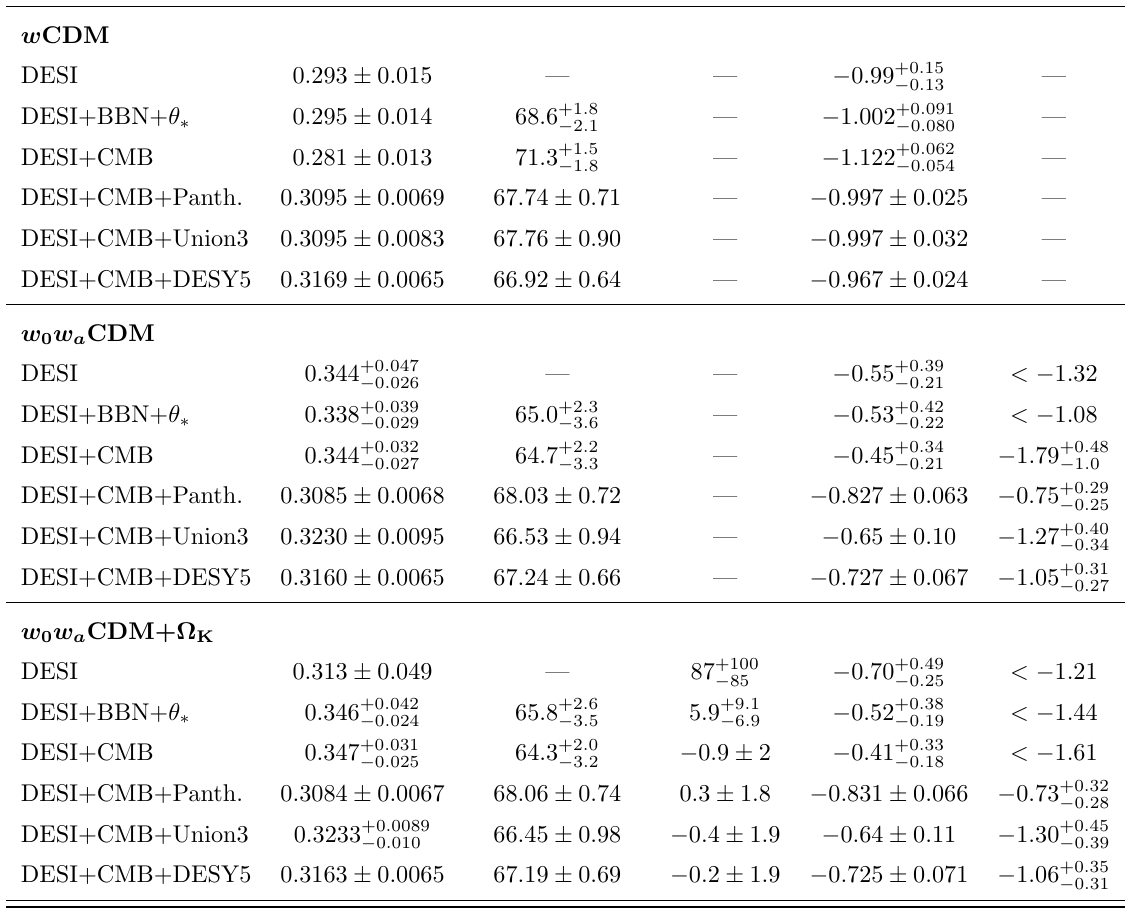
Full tables

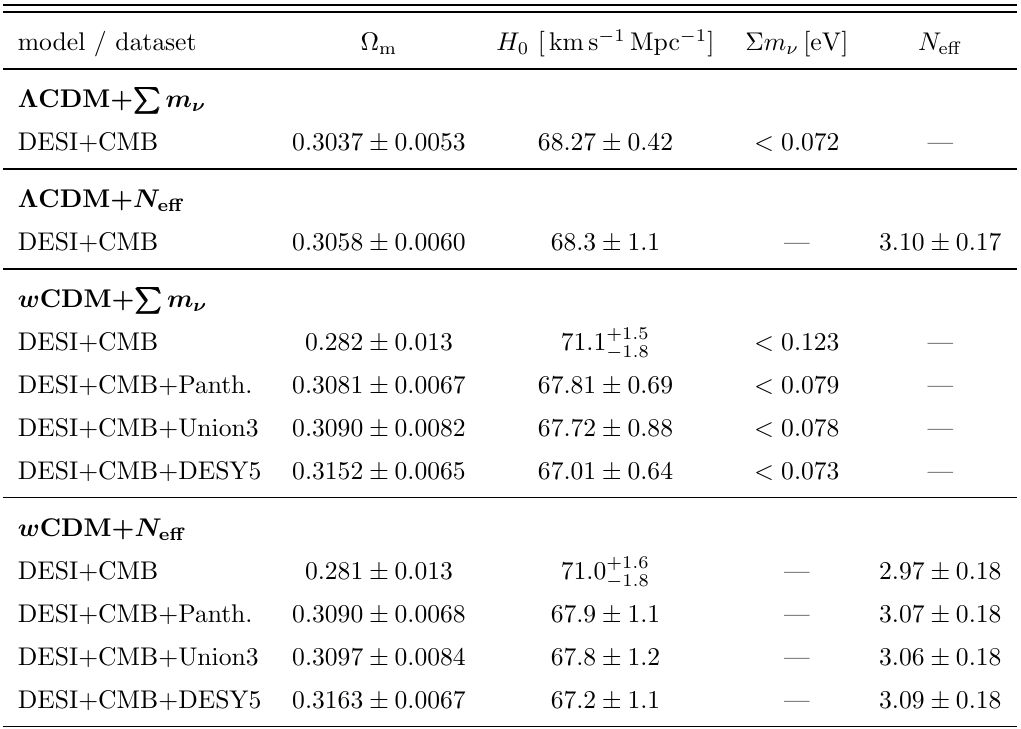
Full tables