Méga-analyse: inférence
bayésienne standard et au niveau du champ

Arnaud de Mattia, Christophe Yèche

CEA Saclay, Irfu/DPhP

Stage IV experiments: DESI

2021 - 2025: 40M redshifts at \(0 < z < 3\)  over \(14 000 \; \mathrm{deg}²\)

Mayall Telescope at Kitt Peak, AZ

5000 robotically-positioned spectroscopic fibers

robotic positioners

Taken from Zhao et al. (2020)

DESI

Credit: NSF

Spectroscopic galaxy surveys

imaging surveys (2014 - 2019) + WISE (IR)

target selection

spectroscopic observations

spectra and redshift measurements

  • two steps: photometry and spectroscopy ⇒ selection effects
  • catalog of angular positions \(\mathrm{R.A.}, \mathrm{Dec.}\) and redshifts \(z\)

DESI Y5 galaxy samples

Bright Galaxies: 14M (SDSS: 600k)

0 < z < 0.4

LRG: 8M (SDSS: 1M)

0.4 < z < 1.1

ELG: 16M (SDSS: 200k)

0.6 < z < 1.6

QSO: 3M (SDSS: 500k)

Lya \(1.8 < z\)

Tracers \(0.8 < z < 2.1\)

Y5 (DR1-DR2-DR3) \(\sim 40\)M galaxy redshifts!

\(z = 0.4\)

\(z = 0.8\)

\(z = 0\)

\(z = 1.6\)

\(z = 2.0\)

\(z = 3.0\)

DESI cosmological constraints

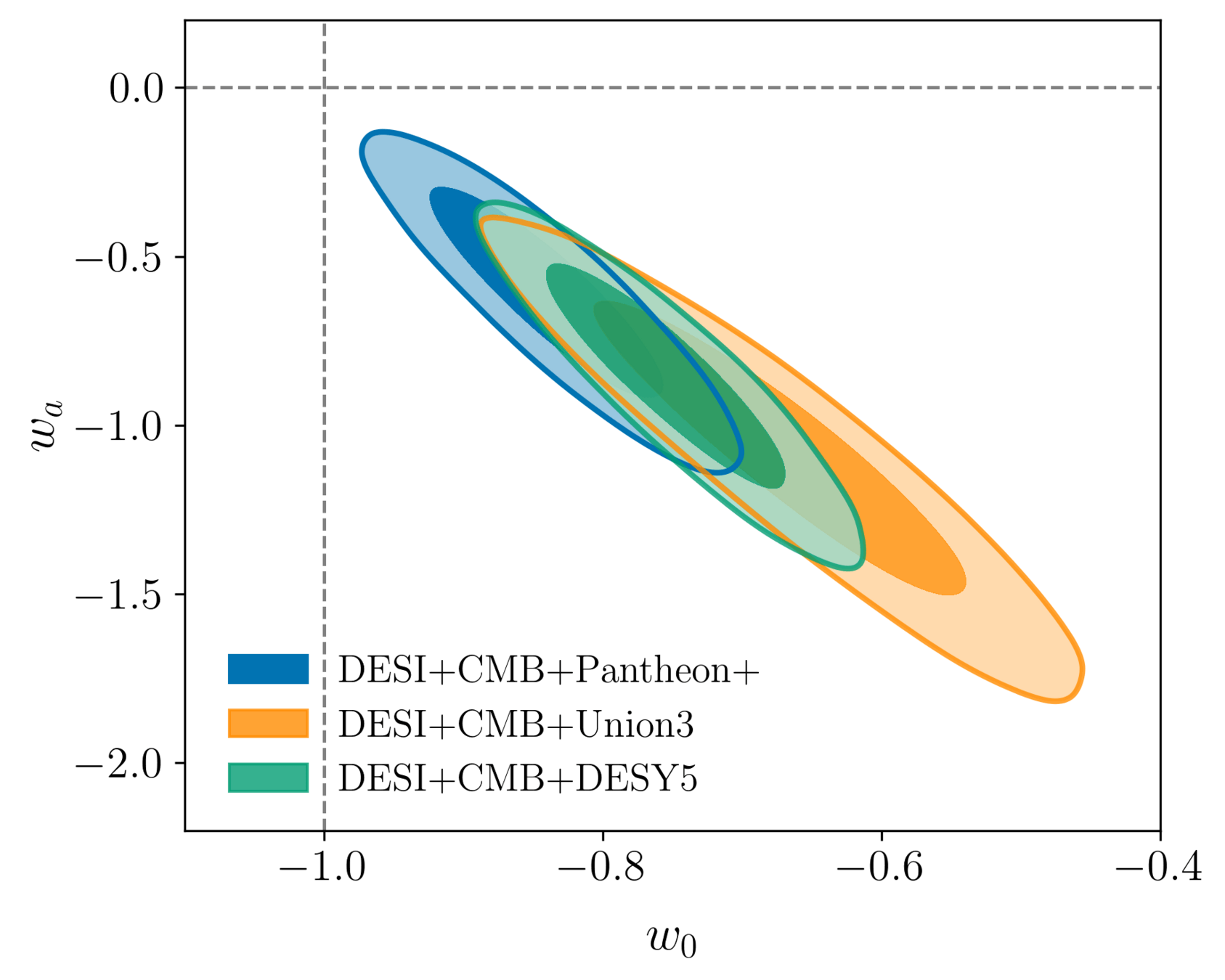
Measuring dark energy

\(\Lambda\)

2024

2025

DESI cosmological constraints

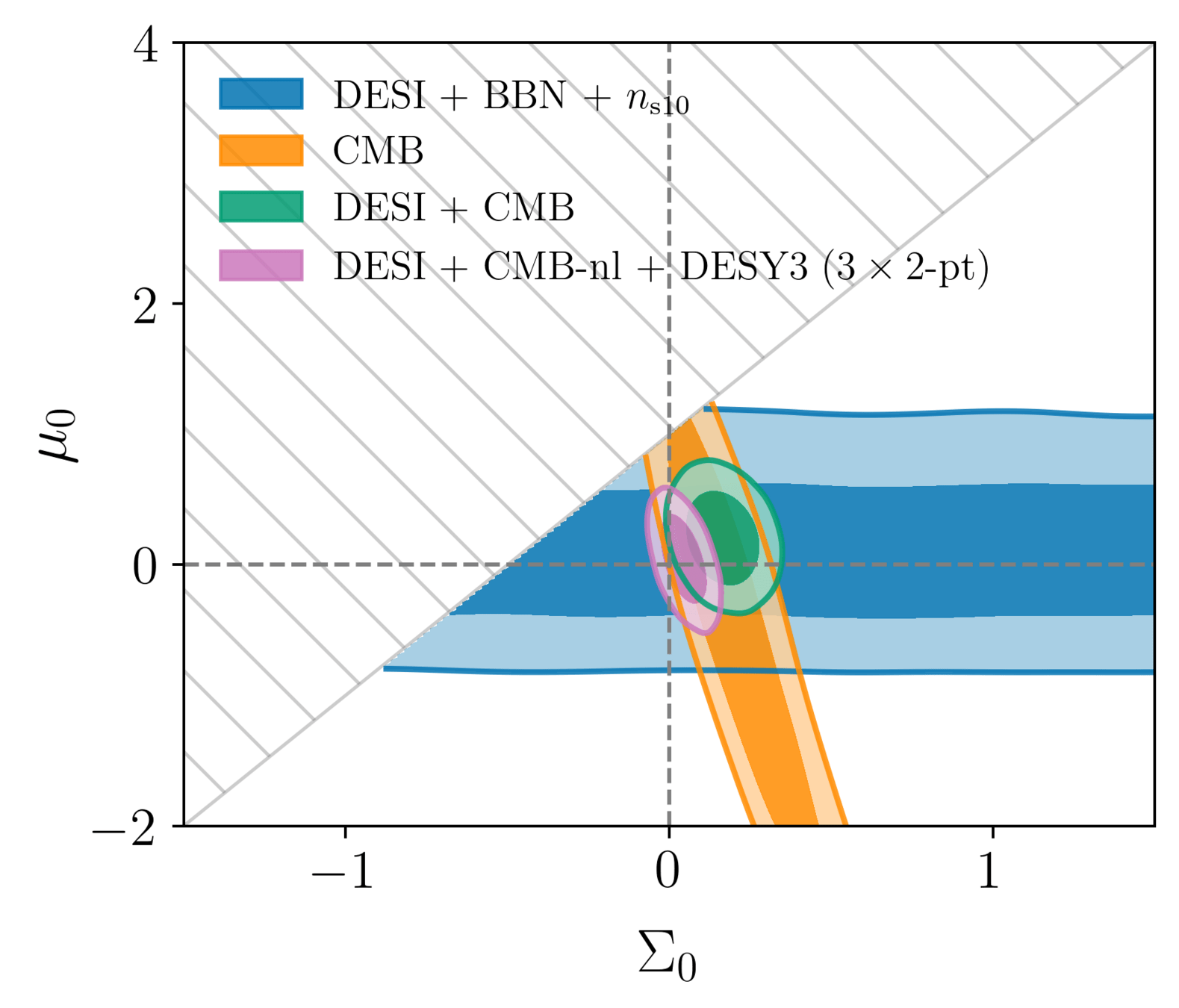
GR

Measuring dark energy

\(\Lambda\)

Testing general relativity

(Isotropic) correlation function

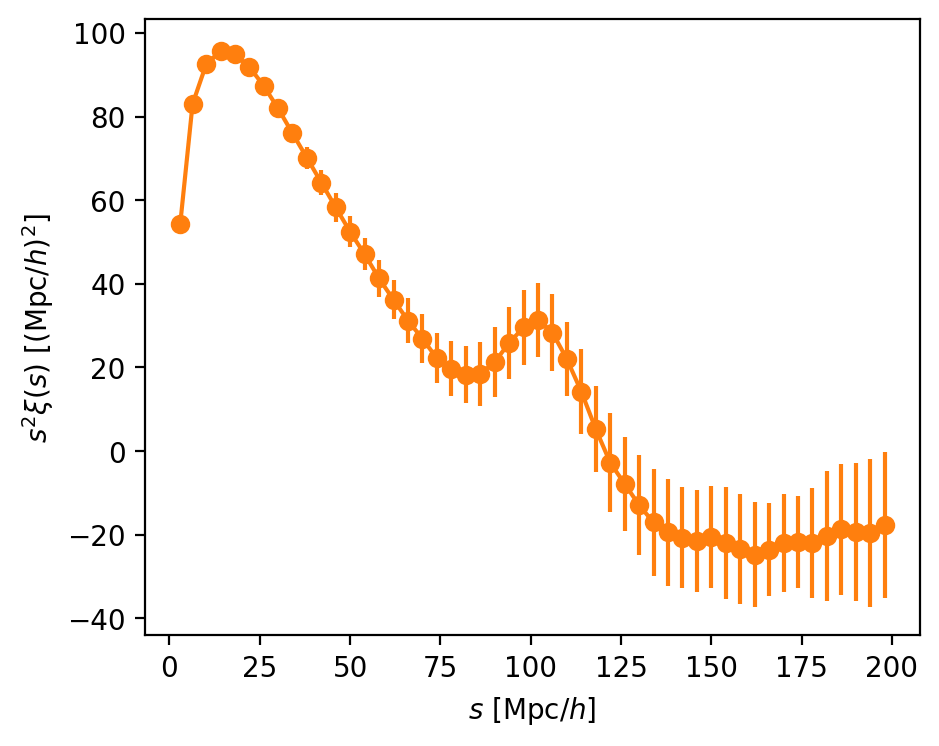
separation between galaxies

correlation function

excess probability that 2 galaxies are close

\(<0\) as \(\int d^3s \xi(s) = 0\)

excess probability that 2 galaxies are close

(Isotropic) power spectrum

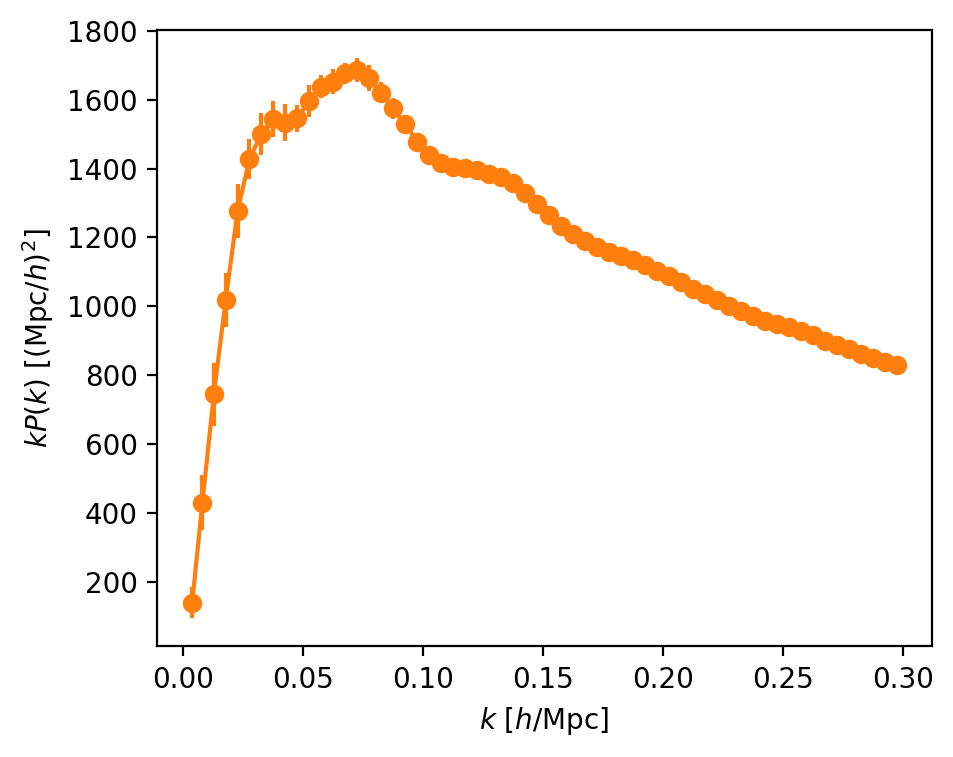
power spectrum

wavenumber

small scales

large scales

Likelihood

Taken from Zhao et al. (2020)

We usually assume a Gaussian likelihood

\ln{p(\mathbf{d} | \mathbf{\theta})} \propto -\frac{1}{2} (\mathbf{d} - \orange{\mathbf{t}}(\red{\mathbf{\theta}}))^T \green{\mathrm{C}}^{-1} (\mathbf{d} - \orange{\mathbf{t}}(\red{\mathbf{\theta}}))

theory model

data vector

(\(P_\ell(k)\) or \(\xi_\ell(s)\))

parameters

covariance matrix

  • Full Shape fit: \(A_\mathrm{s} \text{ or }\sigma_8, \omega_\mathrm{cdm}, h, n_\mathrm{s}\)
  • BAO fit: \(\alpha_\mathrm{iso}, \alpha_\mathrm{ap}\)

+ bias or "nuisance" parameters

analytic or based on fast simulations

We sample the posterior \(p(\red{\mathbf{\theta}} | \mathbf{d}) \propto p(\mathbf{d} | \red{\mathbf{\theta}}) \red{p(\mathbf{\theta})}\)

prior

In a nutshell

Taken from Zhao et al. (2020)

galaxy catalog

galaxy power spectrum (or correlation function)

cosmological constraints

"variance of the density field as a function of scale"

Full Shape

Mega-analysis

Taken from Zhao et al. (2020)

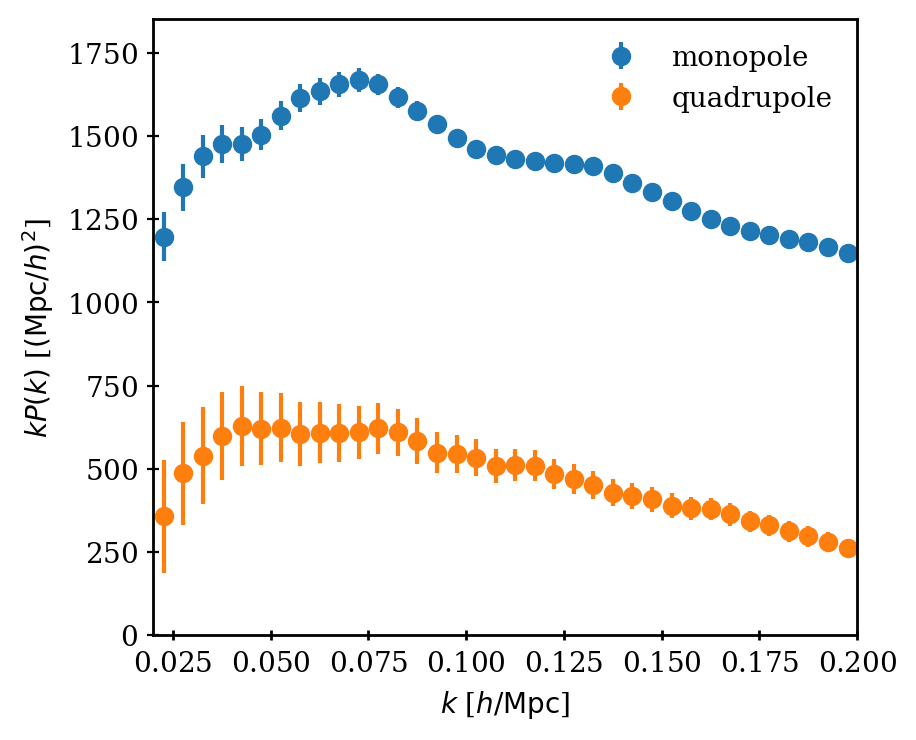
  • In addition to galaxy clustering analyses, cosmological constraints can be obtained with correlations of galaxy clustering and galaxy and CMB lensing
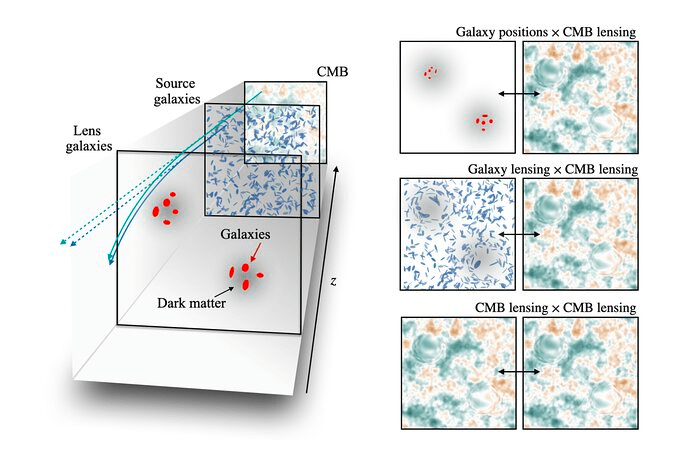
  • For the DESI Y5 sample (timeline: within 2 years)
  • Requires mocks simulating jointly galaxy clustering and lensing

Field-level inference

Fit the observed (discretized) field

Sample the initial cosmic density field

hsimonfroy

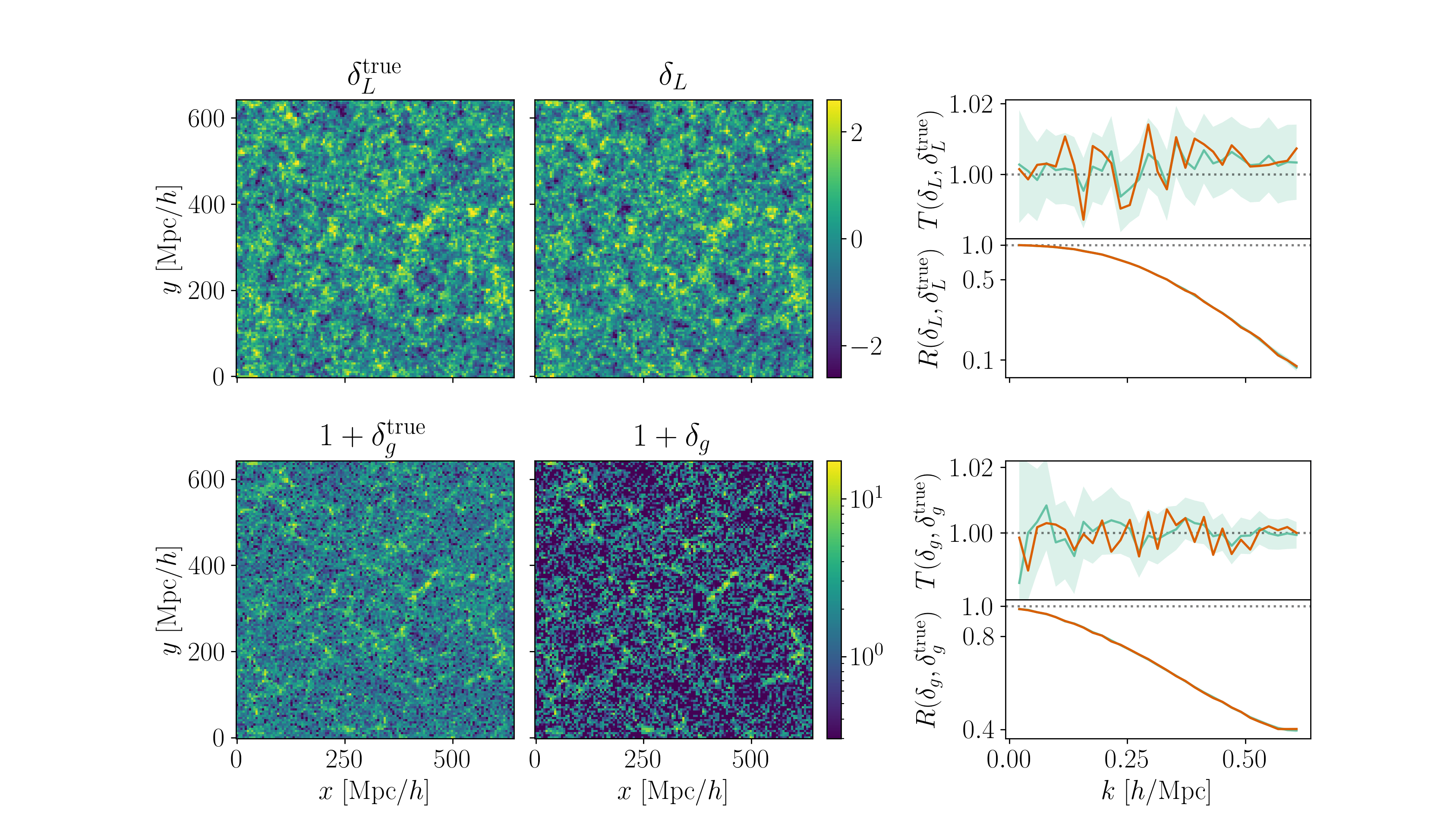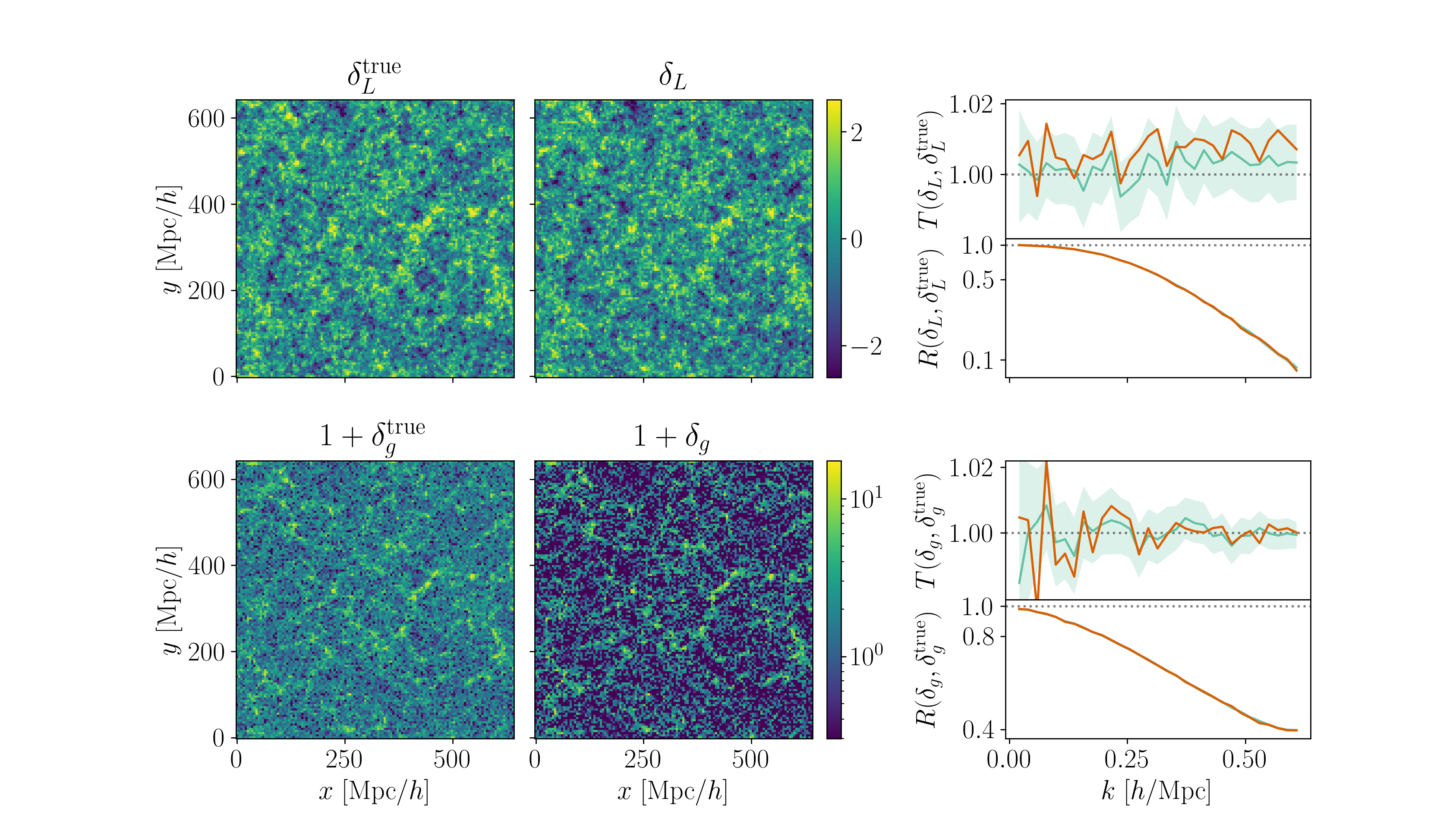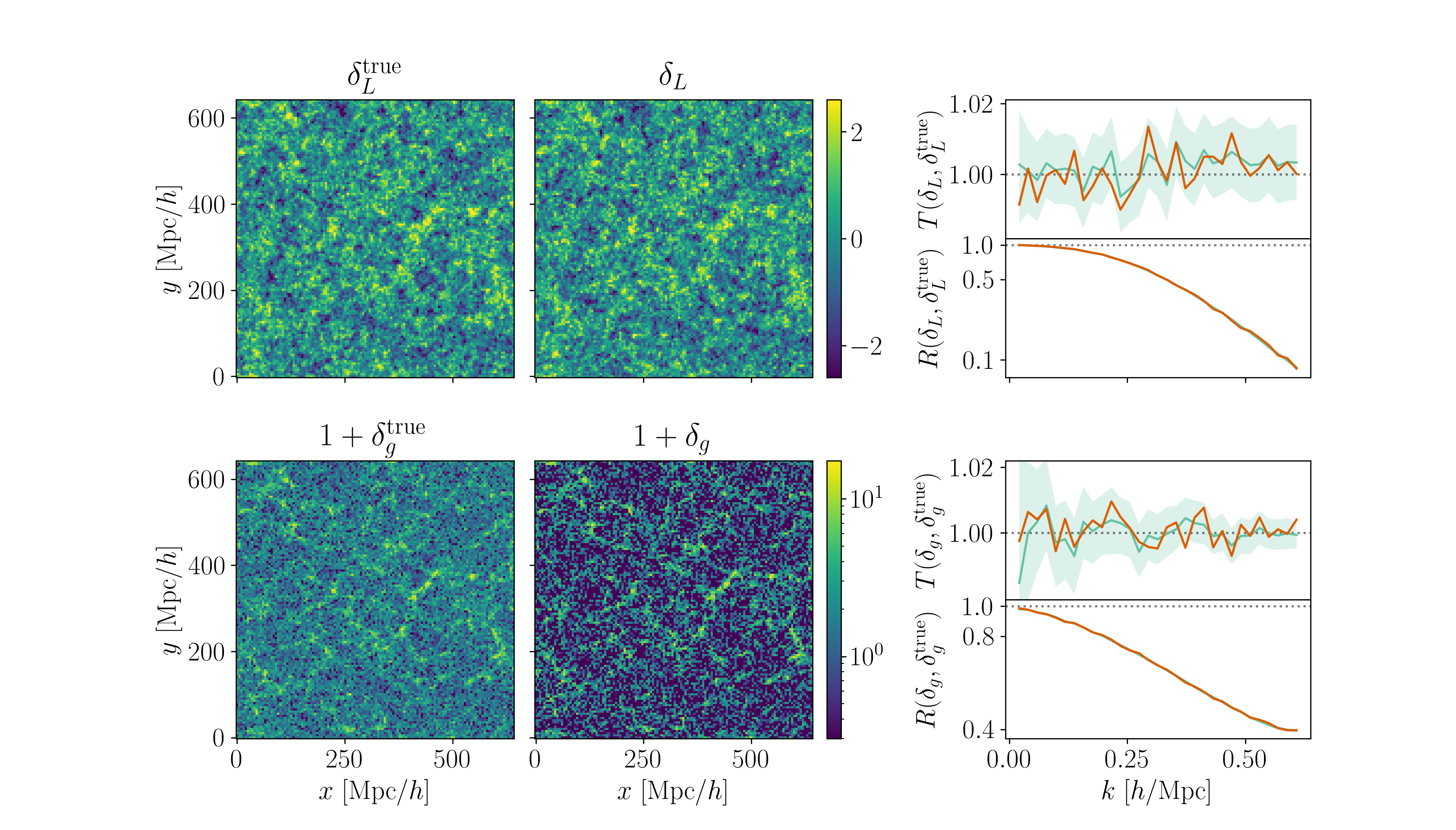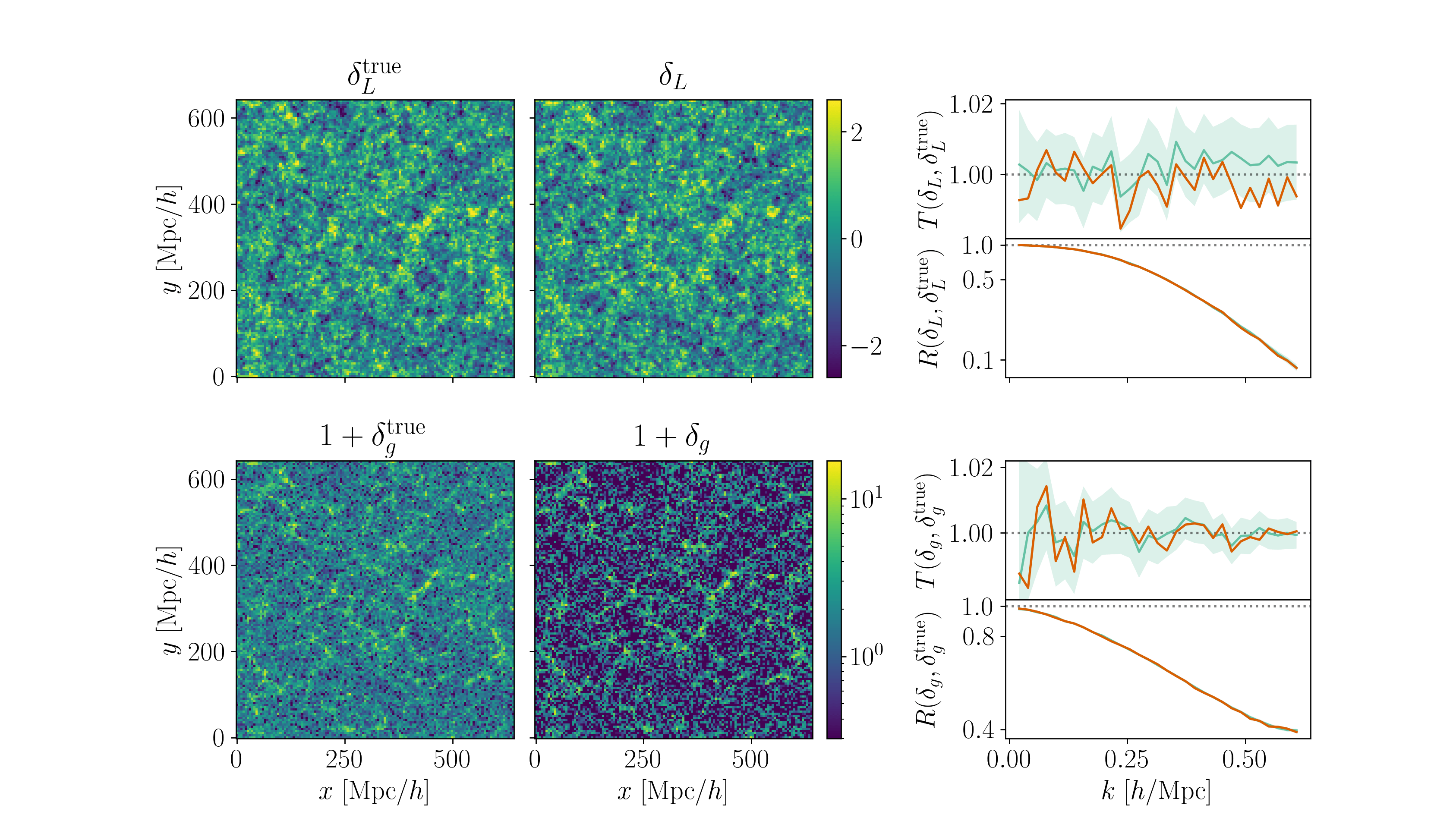
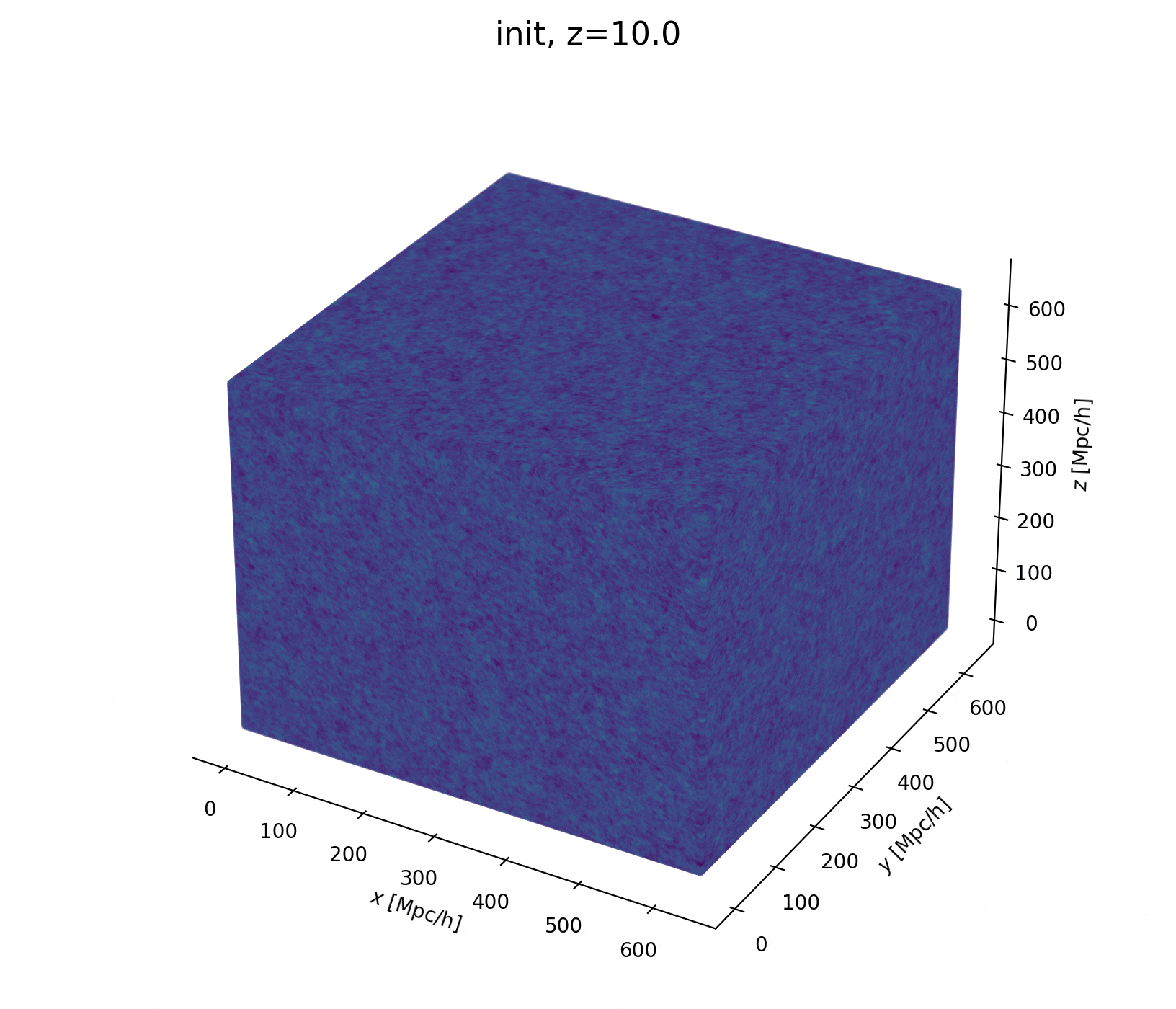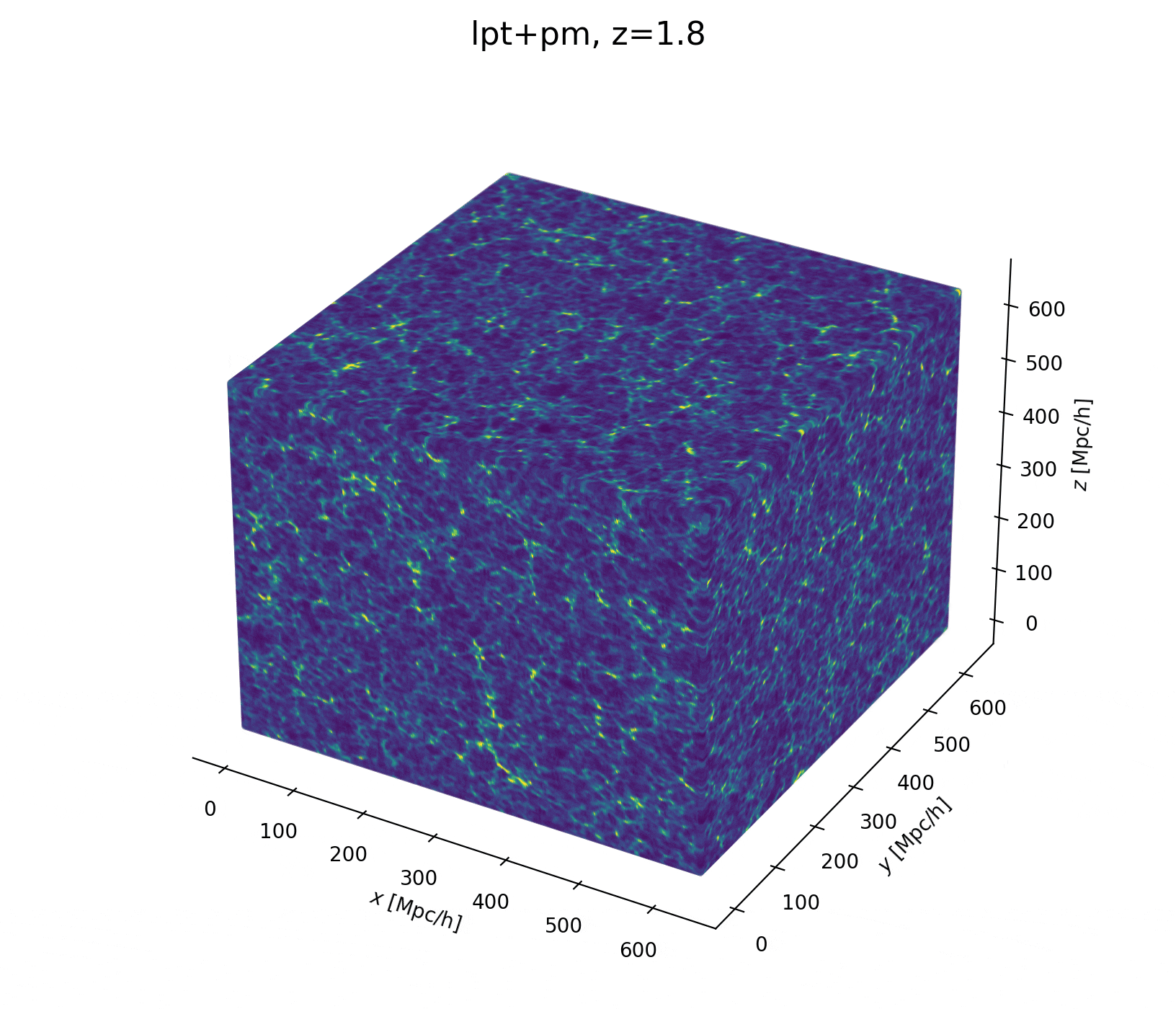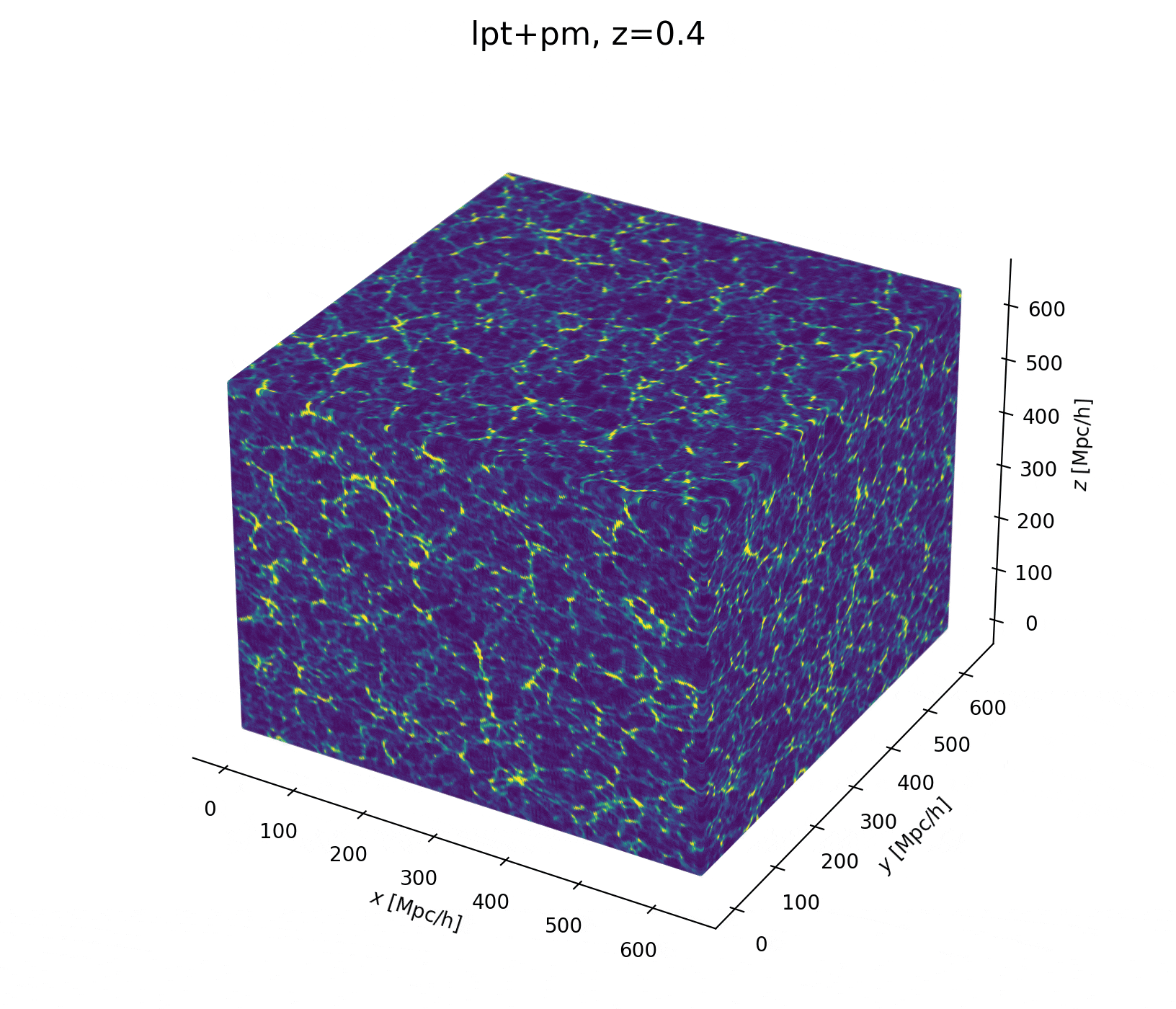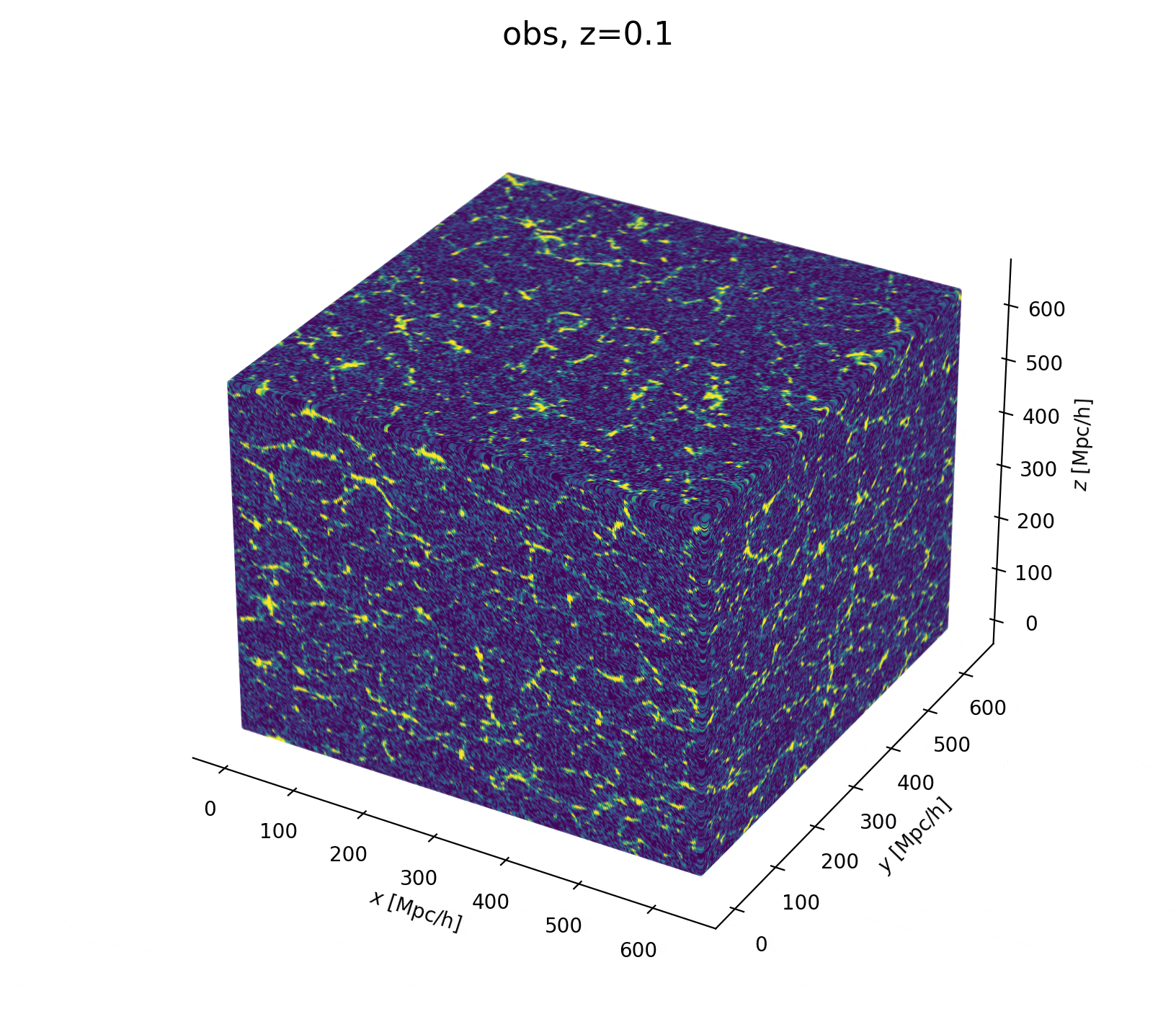
initial density

final density

Field-level inference (benchmark)

Simon-Onfroy+25

more efficient

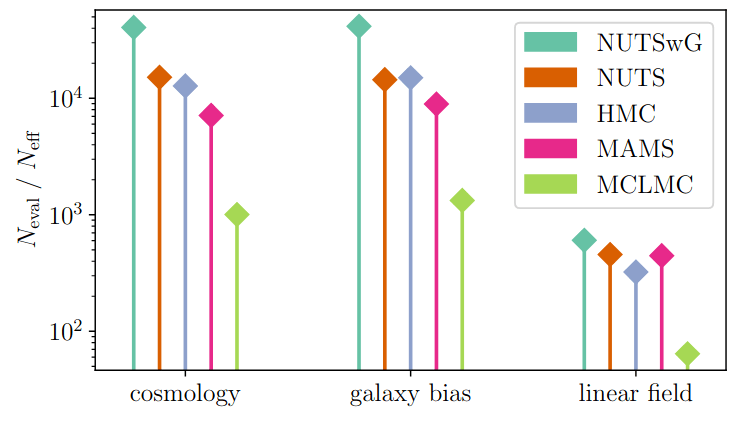
gradient-based samplers

Field-level inference (benchmark)

Simon-Onfroy+25

gradient-based samplers

more efficient

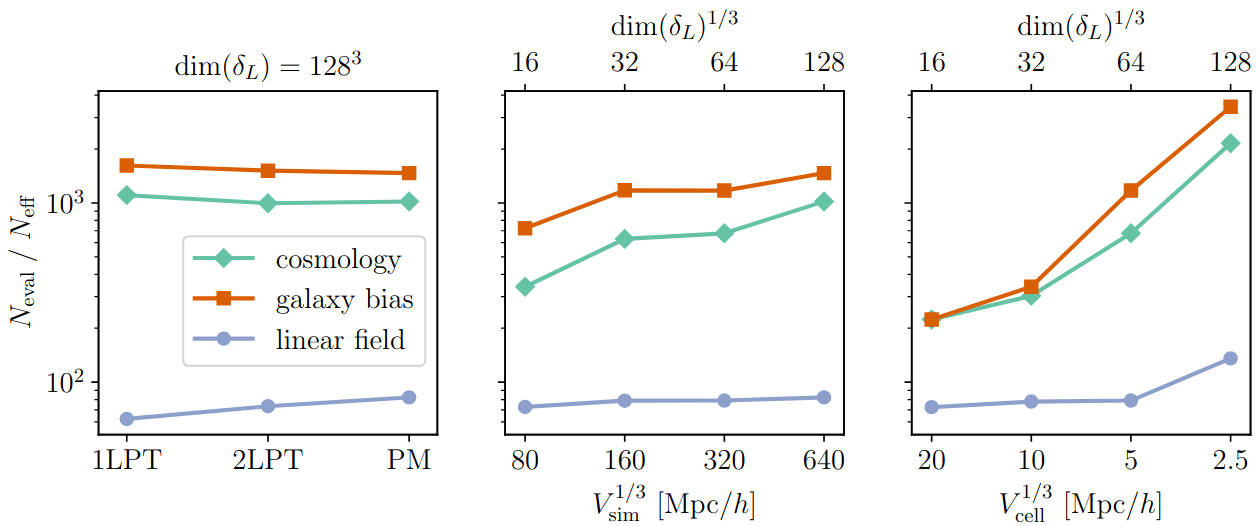
efficiency almost constant with dimension

\(10^6\) parameters \(\simeq 8\) GPU hours

Field-level inference (PNG)

Goal: measure primordial non-Gaussianity with DESI data

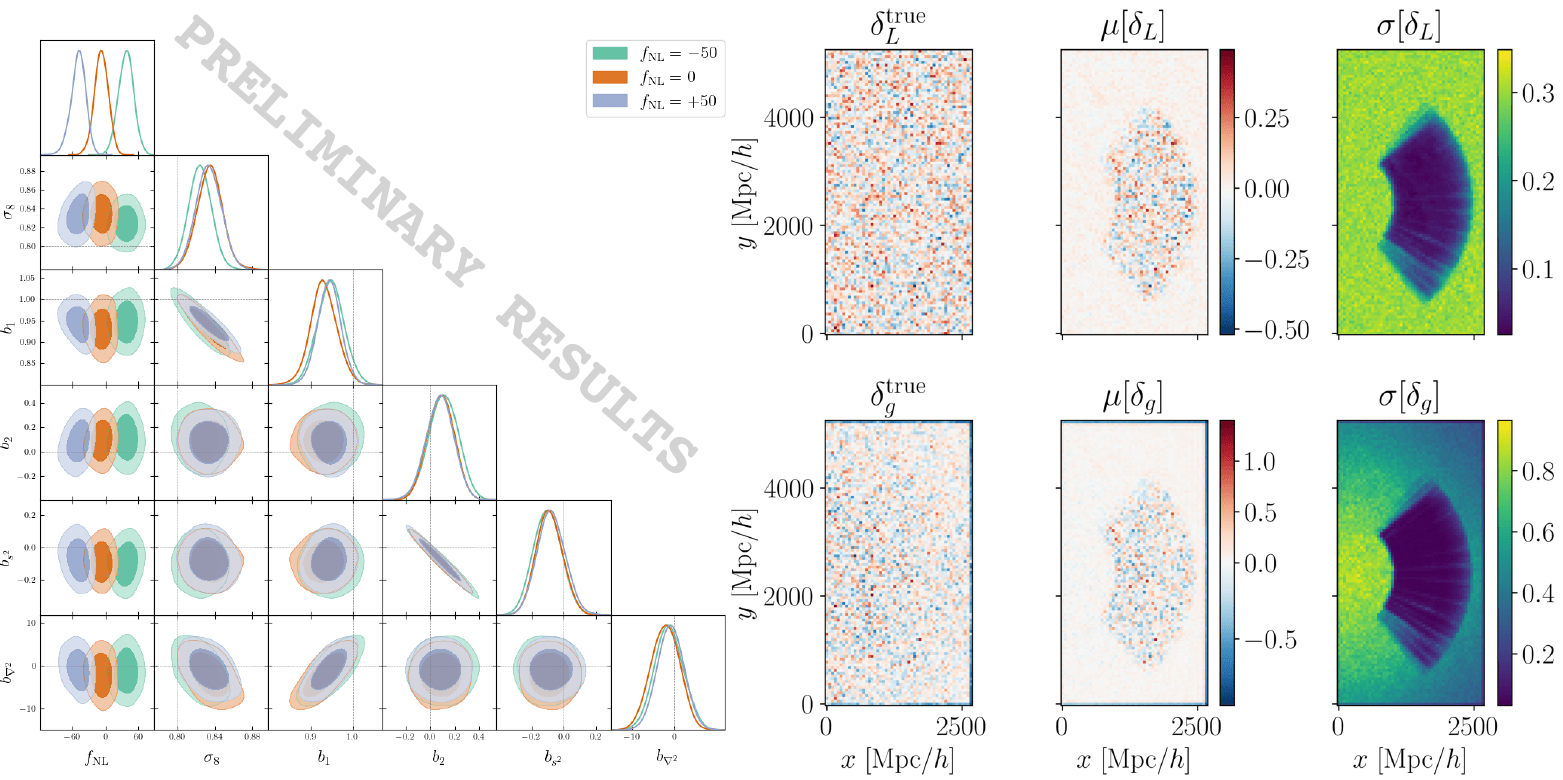
Survey selection function

specify the survey selection function \(\bar{n}\) \(\Rightarrow\) account for systematic effects due to photometry/spectroscopy

Expected density without clustering = angular & radial footprint

Survey selection function \(\bar{n}\)

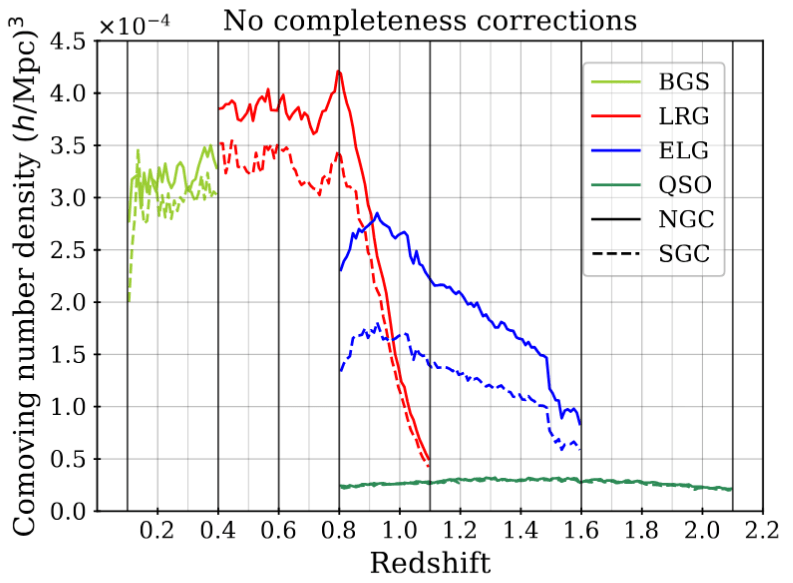
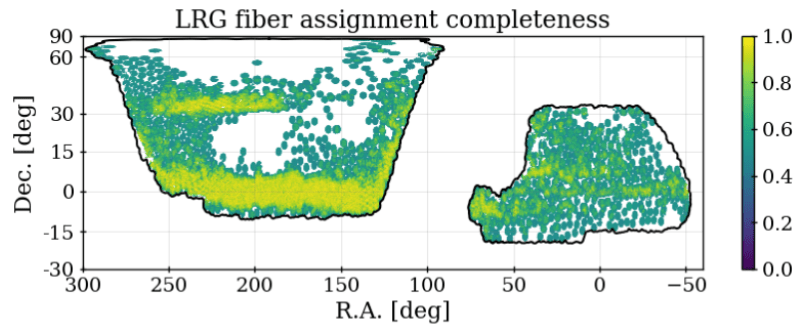
survey selection function \(\bar{n}\)

 Taken from DESI Collaboration et al. 2024