遞迴(上)
Arvin Liu @ Sprout
Question Box
什麼是遞迴?
就是一個函數呼叫自己!
直接看看例子吧!
簡單的遞迴code
the sum of 1 -> n
int f(int x){
if (x == 1) return 1;
return x + f(x-1);
}f(5)= 5 + f(4)
= 5 + [4 + f(3)]
= 5 + [4 + [3 + f(2)]]
= 5 + [4 + [3 + [2 + f(1)]]]
= 5 + [4 + [3 + [2 + [1]]]]
the sum of 1 -> n
int f(int x){
if (x == 1) return 1;
return x + f(x-1);
}f(5) = 5 + 4 + 3 + 3 \text{ (return 1)}
= 5 + 4 + 6 \text{ (return 3)}
= 5 + 10 \text{ (return 6)}
= 15 \text{ (return 10)}
\text{ (return 15)}
斐波那契數列
(Fibonacci number)
Fibonacci - Definition
如果 n = 1 or 2,
f(n) = 1
如果不是,
f(n) = f(n-1)+f(n-2)
Fibonacci - Definition
f(n)=
\begin{cases}
1, \text{if \,n=1\,or \,2}\\
f(n-1)+f(n-2), \text{otherwise}
\end{cases}
f(5)= f(4) + f(3)
= f(3) + f(2) + f(2) + f(1)
= f(2) + f(1) + 1 + 1 + 1
= 5
Fibonacci - Trace Code
f(n)=
\begin{cases}
1, \text{if \,n=1\,or \,2}\\
f(n-1)+f(n-2), \text{otherwise}
\end{cases}
int fib(int x){
if ( x==1 || x==2 ) return 1;
return fib(x-1) + fib(x-2);
}Return就是這個函數=什麼。
Fibonacci - Trace Code
int fib(int x){
if ( x==1 || x==2 ) return 1;
return fib(x-1) + fib(x-2);}fib(5)
fib(4)
fib(3)
fib(3)
fib(2)
fib(2)
fib(1)
fib(2)
fib(1)
1
1
2
1
1
1
2
3
5
遞迴ㄉ小提醒
記得要寫中止條件
例如fib就是n=1或2
思考遞迴條件
fib(n)=fib(n-1)+fib(n-2)
思考要怎麼將大的問題拆成小的問題。
Try try see !
f(n)=
\begin{cases}
1, \text{if \,n=1\,or \,2\,or \, 3}\\
f(n-1)+f(n-2), \text{if n \% 3 = 0 }\\
f(n-1)+f(n-3), \text{otherwise}
\end{cases}
f(20) = 1352,你可以自己驗證看看。
Try try see !
f(20) = 1352,你可以自己驗證看看。
int f(int n){
if(n<=3) return 1;
if(n%3==0) return f(n-1)+f(n-2);
return f(n-1)+f(n-3);
}求出f(100)!
是不是求不出來呢?
記憶化(Memorization)
Memorization
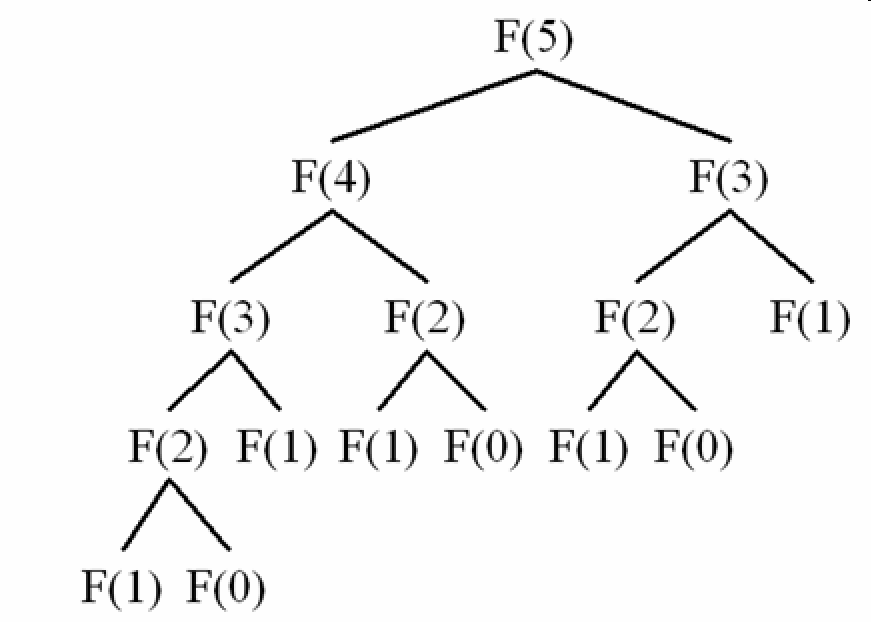
F(3)一樣卻會重算!
Fibonacci - Memorization
int mem[10000]={0}; // 初始化成0。
int fib(int x){
if(n == 1 || n == 2) return 0;
if(mem[x]) // mem[x] = 0 表示沒存過。
return mem[x];
else
return mem[x] = fib(x-1) + fib(x-2);
}如果mem沒存過,就直接算,並且存入mem。
如果算過,就直接回傳。
Memorization - Example
int mem[10000]={0}; // 初始化成0。
int f(int n){
if(n<=3) return 1;
if(mem[n]) return mem[n];
if(n%3==0) return mem[n] = f(n-1)+f(n-2);
return mem[n] = f(n-1)+f(n-3);
}事實上這就是個簡單DP!
DP : Dynamic Programming 動態規劃
DP的其中一個實作方法就是遞迴 + 記憶化
Practice!
Problem Description

Solution - 中止條件

m=1
m=n
Solution - 遞迴規則

C(n,m) =
C(n-1,m-1)+
C(n-1,m)
Solution
#include <iostream>
using namespace std;
int C(int n,int m){
if(m==1 || n==m) return 1;
else return C(n-1,m-1)+C(n-1,m);
}
int main(){
int T;
cin >> T;
while(T--){
int n,m;
cin >> n >> m;
cout << C(n,m) << endl;
}
}Solution + Memorization
#include <iostream>
using namespace std;
int mem[100][100]={0};
int C(int n,int m){
if(m==1 || n==m) return 1;
else if(mem[n][m]) return mem[n][m];
else return mem[n][m] = C(n-1,m-1)+C(n-1,m);
}
int main(){
int T;
cin >> T;
while(T--){
int n,m;
cin >> n >> m;
cout << C(n,m) << endl;
}
}最大公因數 - GCD
輾轉相除法
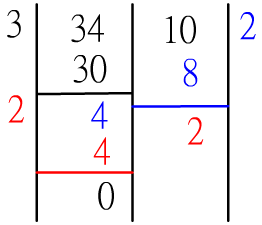
如果 a>b
則 a 會變成 a%b,
並算GCD(a%b,b)
輾轉相除法
如果 a>b
則 a 會變成 a%b,並算GCD(a%b,b)
換句話說:
如果 a>b
GCD(a,b) = GCD(a%b , b)
輾轉相除法
如果 a>b,
GCD(a,b) = GCD(a%b , b)
= GCD(b, a%b)
為什麼a%b,b要換位子?
因為要讓左邊的數字比較大。
因為 b > a%b
GCD
int GCD(int a,int b){
if (b==0) return a;
return GCD(b,a%b);
}想想看,
如果呼叫GCD(x,y),其中x<y會怎麼樣?
遞迴還可以幹嘛?
Everything You Want!

爆破別人的密碼?
a
zzzzzzzz
aa
aaa
...
b
ba
...
...
...
密碼的所有可能

爆搜最佳解!
a
zzzzzzzz
aa
aaa
...
b
ba
...
...
...
密碼的所有可能