PHC6016 Social Epidemiology

 

Multilevel Approaches

 

October 19, 2017

 

Hui Hu, PhD

huihu@ufl.edu

Introduction

 

Linear Mixed-Effects Model

 

Generalized Linear Mixed-Effects Model

Introduction

  • We usually assume the samples drawn from targeted population are independent and identically distributed (i.i.d.).

 

  • This assumption does not hold when we have data with multilevel structure:
    - clustered and nested data (i.e. individuals within areas)
    - longitudinal data (i.e. repeated measurements within individuals)
    - non-nested structures (i.e. individuals within areas and belonging to some subgroups such as occupations)
     
  • Samples within each group are dependent, while samples between groups stay independent
     
  • Two sources of variations:
    - variations within groups
    - variations between groups
  • A longitudinal study:
    - n = 3
    - t = 3
     
  • Complete pooling
    - poor performance
     
  • No pooling
    - infeasible for large n
     
  • Partial pooling
  • An alternative solution: include categorical individual indicators in the traditional linear regression model.
     
  • Why do we still need mixed-effects models?
  1. Account for both individual- and group-level variations when estimating group-level coefficients.
     
  2. Easily model variations among individual-level coefficients, especially when making predictions for new groups.
     
  3. Allow us to estimate coefficients for specific groups, even for groups with small n

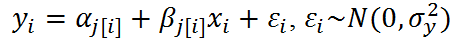
Fixed and Random Effects

  • Random Effects: varying coefficients
  • Fixed Effects: varying coefficients that are not themselves modeled

How to decide whether to use fixed-effects or random-effects?

When do mixed-effects models make a difference?

Fixed and Random Effects

Two extreme cases:

  • when the group-level variation is very little
    - reduce to traditional regression models without group indicators (complete pooling)
  • when the group-level variation is very large
    - reduce to traditional regression models with group indicators (no-pooling)

Little risk to apply a mixed-effects model

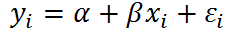
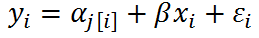
What's the difference between no-pooling models and mixed-effects models only with varying intercepts?

  • In no-pooling models, the intercept is obtained by least squares estimates, which equals to the fitted intercepts in models that are run separately by group.
  • In mixed-effects models, we assign a probability distribution to the random intercept: 

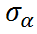
Intraclass Correlation (ICC)

shows the variation between groups

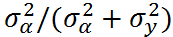
ICC ranges from 0 to 1:

  • ICC -> 0: the groups give no information (complete-pooling)
  • ICC -> 1: all individuals of a group are identical (no-pooling)

Intraclass Correlation (ICC)

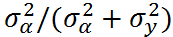
ICC ranges from 0 to 1:

  • ICC -> 0: "hard constraint" to 
  • ICC -> 1: "no constraint" to
  • Mixed-effects model: "soft constraint" to 

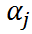
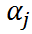
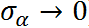
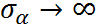
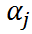
This constraint has different effects on different groups:

  • For group with small n, a strong pooling is usually seen, where the value of     is close to the mean      (towards complete-pooling)
  • For group with large n, the pooling will be weak, where the value of    is far away from the mean      (towards no-pooling)

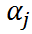
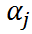
Linear Mixed-Effects Model

Pull the codes and dataset: https://github.com/benhhu/R-Mixed-Effects-Model

Load the Packages and Data

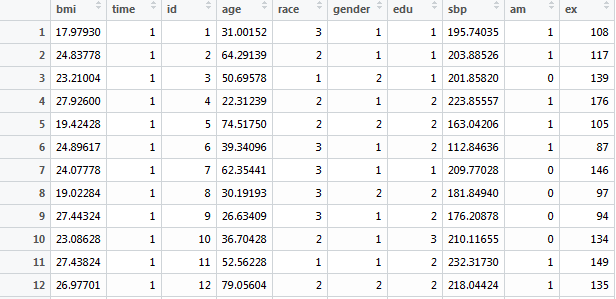
1,000 participants

5 repeated measurements

 

bmi

time

id

age

race: 1=white, 2=black, 3=others

gender: 1=male, 2=female

edu: 1=<HS, 2=HS, 3=>HS

sbp

am: 1=measured in morning

ex: #days exercised in the past year

Varying-intercept Model with No Predictors

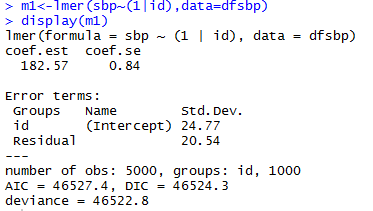
allows intercept to vary by individual

estimated intercept, averaging over the individuals

estimated variations

Varying-intercept Model with an individual-level predictor

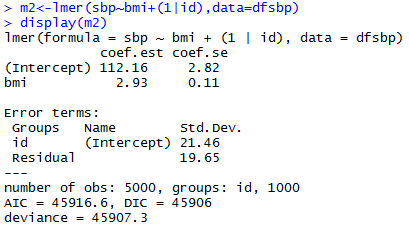
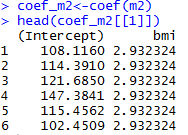
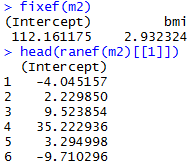
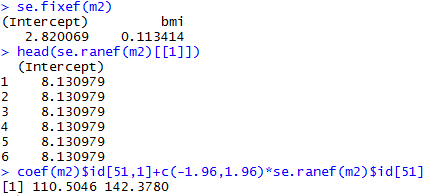
Varying-intercept Model with both individual-level and group-level predictors

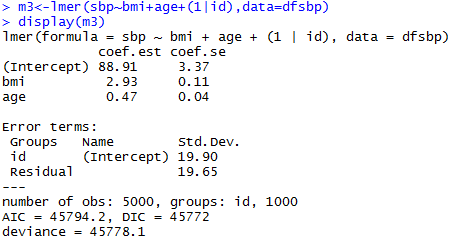
Varying Slopes Models

With only an individual-level predictor

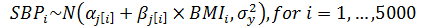
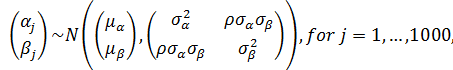
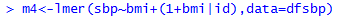
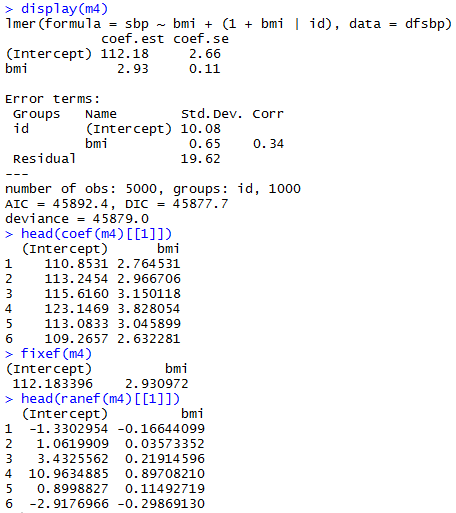
Varying Slopes Models

Add a group-level predictor

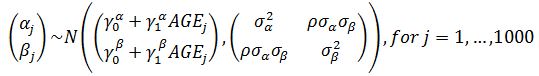
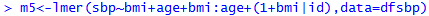
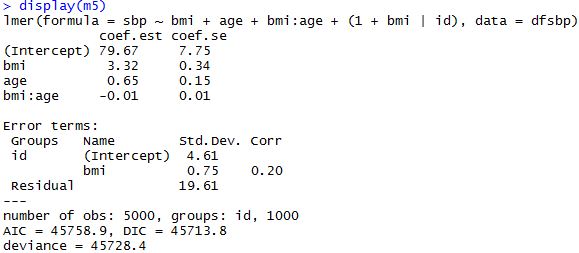
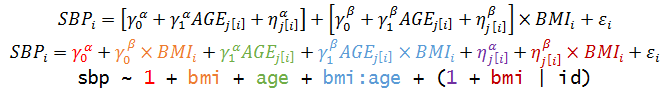
Non-nested Models

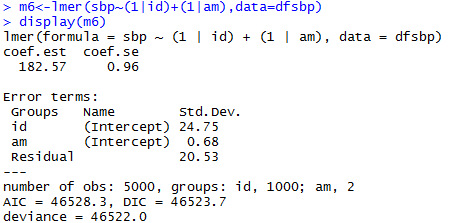
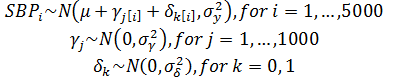
Generalized Linear Mixed-Effects Model

Mixed-Effects Logistic Model

Empty model

Mixed-Effects Logistic Model

Add bmi and race

Mixed-Effects Poisson Model

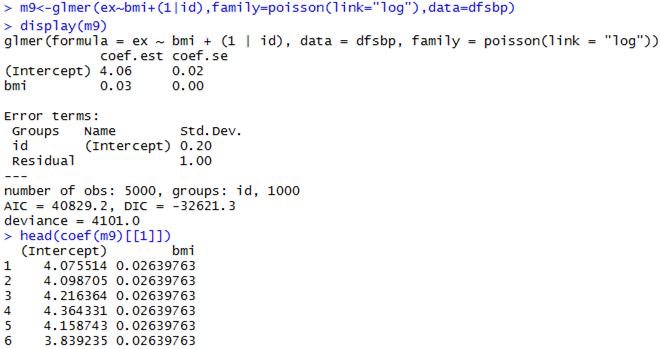
Parameter Estimation Algorithms

  • ML: maximum likelihood
     
  • REML: restricted maximum likelihood
    - default in lmer()
  • PQL: pseudo- and penalized quasilikelihood
     
  • Laplace approximations
    - default in glmer()
  • GHQ: Gauss-Hermite quadrature
     
  • McMC: Markov chain Monte Carlo

Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, et al. 2009. Generalized linear mixed models: A practical guide for ecology and evolution. Trends in ecology & evolution 24:127-135.

Mixed-Effects Model vs. GEE

Mixed-Effects Model Marginal Model with GEE
Distributional assumptions Yes No
Population average estimates Yes Yes
Group-specific estimates Yes No
Estimate variance components Yes No
Perform good with small n Yes No