PHC6194 SPATIAL EPIDEMIOLOGY

Disease Clustering

Hui Hu Ph.D.

Department of Epidemiology

College of Public Health and Health Professions & College of Medicine

February 28, 2018

Introduction

 

Global Clustering
 

Local Clustering

 

Lab: Disease Clustering

Introduction

Spatial Patterns

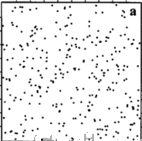
Random

Cluster

Regular

Disease Cluster

  • The occurrence of a greater than expected number of cases of a particular disease within a group of people, a geographic area, or a period of time.
     
  • A collection of disease occurrence:
    - of sufficient size and concentation to be unlikely to have occurred by chance, or
    - related to each other through some social or biological mechanism, or having a common relationship with some other events or circumstance
     
  • Spatial aggregation of disease events may only be a function of the distribution of population
     
  • Disease cluster: residual spatial variation in risk after known influence have been accounted for

Purposes of Disease Cluster Detection

  • Confirmatory purpose
    - verify if a perceived cluster exists:
      e.g. excess risk reported by citizens
     
  • Exploratory purpose
    - search for spatial patterns
     
  • Identification of clusters can lead to interventions

Methods of Disease Cluster Detection

  • Global clustering:
    - non-specific methods
    - only detect if cluster exists, without specific location
     
  • Local clustering:
    -  specific methods
    -  shows the specific locations where clusters exist
    -  two methods: non-focused and focused

Global Clustering

Global Clustering (Non-specific Methods)

  • Evaluate whether clustering exist as a global phenomena throughout the study region, without pinpointing the location of specific cluster
     
  • e.g. the analysis of overall clustering tendency of some disease incidence in a study region

Tests for Global Clustering

  • Over 100 different testing methods for global clustering in the field
     
  • Some widely-used methods:
    -  for aggregated data:
       Moran's I
       Geary's C
    -  for points data:
       KNN

Moran's I

  • Moran's I is a global index of spatial auto-correlation
    -  to quantify the similarity of an variable among areas that are defined as spatially related
     
  • Calculation:



     
  • N: number of spatial units indexed by i and j
  • X: the variable of interest
  • wij: a matrix of spatial weights
I={{N}\over {\sum_i(X_i-\bar X)^2}}\times {{\sum_i\sum_jw_{ij}(X_i-\bar X)(X_j-\bar X)}\over {\sum_i\sum_jw_{ij}}}
I=N∑i(Xi−X¯)2×∑i∑jwij(Xi−X¯)(Xj−X¯)∑i∑jwijI={{N}\over {\sum_i(X_i-\bar X)^2}}\times {{\sum_i\sum_jw_{ij}(X_i-\bar X)(X_j-\bar X)}\over {\sum_i\sum_jw_{ij}}}

Moran's I (cont'd)

  • Moran's I coefficient of auto-correlation is similar to Pearson's correlation coefficient
     
  • I>0
    -  positive spatial auto-correlation
    -  neighboring regions tend to have similar values
     
  • I<0
    -  negative spatial autocorrelation
    -  neighboring regions tend to have inverse values
     
  • Results will depend on specification of the weight matrix

Geary's C

  • Also called Geary's contiguity ratio
     
  • Another widely used global index of spatial auto-correlation
     
  • Calculation:



     
  • N: number of spatial units indexed by i and j
  • X: the variable of interest
  • wij: a matrix of spatial weights
C={{N-1}\over {2\sum_i(X_i-\bar X)^2}}\times {{\sum_i\sum_jw_{ij}(X_i-X_j)^2}\over {\sum_i\sum_jw_{ij}}}
C=N−12∑i(Xi−X¯)2×∑i∑jwij(Xi−Xj)2∑i∑jwijC={{N-1}\over {2\sum_i(X_i-\bar X)^2}}\times {{\sum_i\sum_jw_{ij}(X_i-X_j)^2}\over {\sum_i\sum_jw_{ij}}}

Geary's C (cont'd)

  • Geary's C ranges from 0 to 2
     
  • Low value of Geary's C denote positive auto-correlation
    -  0 indicates perfect positive spatial auto-correlation
     
  • High value of Geary's C denote negative auto-correlation
    -  2 indicates perfect negative spatial auto-correlation
     
  • 1 indicates no auto-correlation

KNN

  • Proposed by Cuzick and Edward
     
  • To detect the possible clustering of sub-populations within a clustered or non-uniformly-spread overall population
     
  • Based on the locations of cases and randomly selected controls from a specified region

KNN (cont'd)

  • Central idea of the method: to find how many of the K nearest neighbors of a cases that are also cases





     
  • A weight matrix based on KNN
    -  wij=1 if location j is among k nearest neighbors of location i
     
  • The test statistics:

     
  • 𝛿=1 if the point is a case, 𝛿=0 if the point is a control
T_k=\sum_{i=1}^n \sum_{j=1}^n w_{ij}\delta_i\delta_j
Tk=∑i=1n∑j=1nwijδiδjT_k=\sum_{i=1}^n \sum_{j=1}^n w_{ij}\delta_i\delta_j

KNN (cont'd)

  • Monte Carlo test under the random labeling hypothesis is used to test the significance
     
  • The rank of the test statistic is based on the data observed among the values from the randomly labeled data, which allows calculation of the p-value

Local Clustering

Local Clustering Test

  • Additionally specify the location and can be extended to also consider temporal patterns
     
  • Focused tests:
    -  investigate whether there is an increased risk of disease around a pre-determined point
    -  e.g. Superfund site; A nuclear power plant; A waste dumping site
     
  • Non-focused tests:
    -  identify the location of all potential clusters in the study region

Focused Tests

  • H0: there is no cluster of cases around the foci
     
  • The Lawson Waller test
    -  also called Berman's Z1 test
    -  H0: yi~ Poisson(ni*r)
    -  H1: yi~ Poisson(    ni*r (1+εθi)), where θi represents exposure to the foci experienced by population in region i; ε represents a small, positive constant
    -  what is the relative risk comparing people in region i with people with no exposure
     
  • The Lawson Waller score


    -  where θi is defined by the inverse distance of each region from the foci
    -  usually standardized to range from 0 to 1
T_{sc}=\sum_{i=1}^N\theta_i(y_i-rn_i)
Tsc=∑i=1Nθi(yi−rni)T_{sc}=\sum_{i=1}^N\theta_i(y_i-rn_i)

Non-focused Tests

  • Aggregated data:
    -  Local Indicators of Spatial Auto-correlation (LISA)
    -  Local Getis-Ord G statistics
    -  Spatial scan statistics
     
  • Point data:
    -  Openshaw's Geographical analysis Machine (GAM)
    -  Turnbull's cluster evaluation permutation procedure (CEPP)
    -  Spatial scan statistics

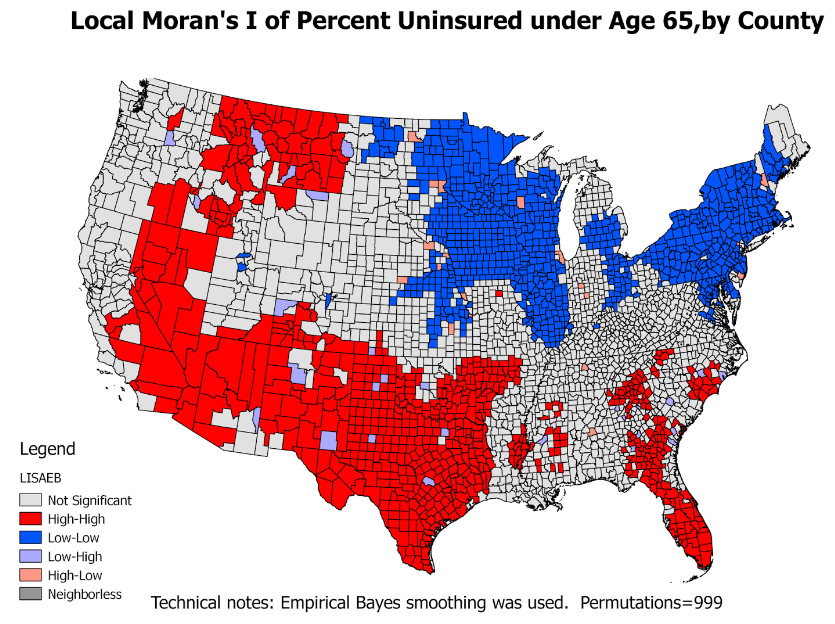
LISA

  • Also called Local Moran's I
     
  • LISA values allow for the computation of its similarity with its neighbors and also to test its significance
     
  • LISA divides the study region into 5 categories:
    -  high-high locations: also known as hot spots
    -  low-low locations: also known as cold spots
    -  high-low locations: potential spatial outliers
    -  low-high locations: potential spatial outliers
    -  locations with no significant local auto-correlation

Local Getis-Ord G Statistic

  • The proportion of all x values in the study area accounted for by the neighbors of location i


     
  • G will be high where high values cluster (hot spot)
    -  G will be low where low values cluster (cold spot)
G_i(d)={{\sum_jw_{ij}x_j}\over {\sum_jx_j}}
Gi(d)=∑jwijxj∑jxjG_i(d)={{\sum_jw_{ij}x_j}\over {\sum_jx_j}}

Spatial Scan Statistic

  • Steps:
    -  search over a given set of spatial regions
    -  find those regions which are most likely to be clusters
    -  correctly adjust for multiple hypothesis testing

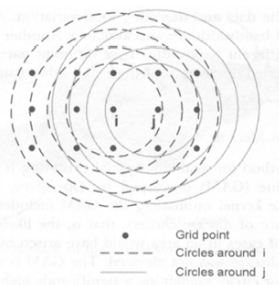
Search Over a Given Set of Spatial Regions

  • Create a regular or irregular grid of centroids covering the whole study area
     
  • Create an infinite number of circles around each centroid, with the radius ranging from 0 to a maximum which includes at most 50% of the population
     
  • A circular scanning window is placed at different coordinates with radius that vary from 0 to some set upper limit.

Find Regions that are Most Likely to be Clusters

  • For each location and size of window
    H   = elevated risk within window as compared to outside of window
     
  • Is there any region with disease rates significantly higher inside the circle than outside the circle ?
     
  • For each circle, obtain the actual and expected number of cases inside and outside the circle, and calculate likelihood function

A

Find Regions that are Most Likely to be Clusters (cont'd)

  • Generate random replicas of the dataset under the null-hypothesis of no clusters (Monte Carlo sampling)
     
  • Compare most likely clusters in real and random datasets (likelihood ratio test)

Properties of Spatial Scan Statistics

  • Adjusts for inhomogeneous population density
     
  • Simultaneously tests for clusters of any size and any location, by using circular windows with continuously variable radius
     
  • Accounts for multiple testing
     
  • Possibility to include confounding variables
     
  • Can be used with both aggregated and point data

Lab: Disease Clustering

git pull