Looking into solving SPP in GCS with Distributed Algorithms
Short Talk RLG
October 23rd 2023
Bernhard Paus Graesdal
Disclaimer: Only worked on this for two weeks! Very preliminary
High Level Motivation
1. Solve large GCS instances
2. Leverage parallel computation
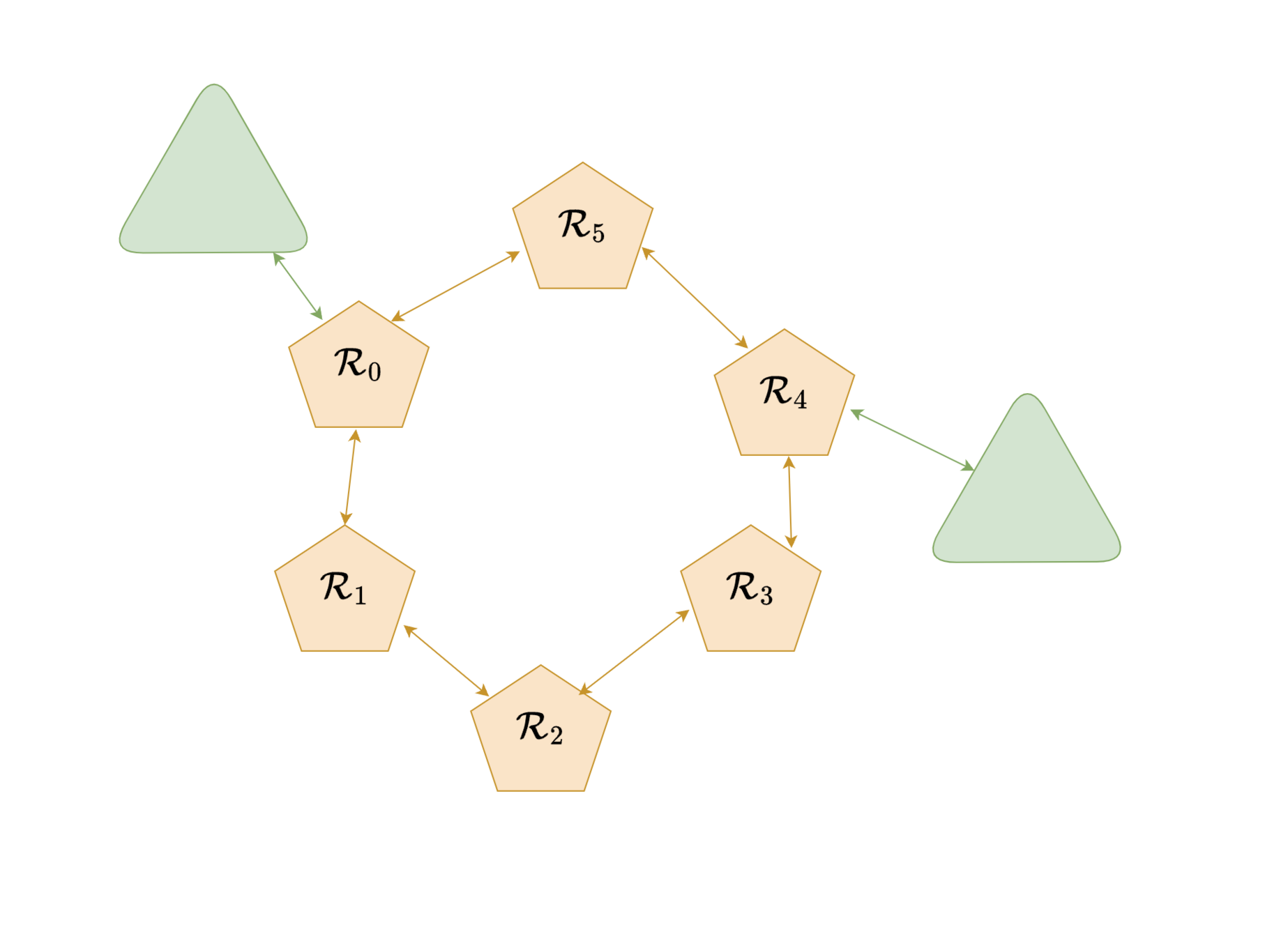
Motivational example : Large contact graphs
- Very large graphs
- Consistent structure for different problems
- Graph is very sparse
- (each node is only connected to two neighboring nodes)
Agenda
- Background on ADMM
- Two proposed ADMM formulations for GCS
- Some preliminary results
Great reference on ADMM:
[1] S. Boyd, “Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers,” FNT in Machine Learning, 2010
\begin{aligned}
\min \quad& f(x) + g(z) \\
\text{s.t.}
\quad & Ax + Bz = c
\end{aligned}
- General ADMM problem looks like this:
- \(f: \R^n \rightarrow \R \cup \{ \infty \} \) and \(g: \R^m \rightarrow \R \cup \{ \infty \} \) are convex functions
- Notice that they can take infinite value (this is how we encode other constraints)
- \(A \in \R^{l \times n}\) and \(B \in \R^{l \times m}\)
- \(x \in \R^n\) and \(z \in \R^m\) are optimization variables
ADMM Introduction (1/3)
ADMM Introduction (2/3)
\begin{aligned}
\min \quad& f(x) + g(z) \\
\text{s.t.}
\quad & Ax + Bz = c
\end{aligned}
- Form the Augmented Lagrangian
\begin{aligned}
L_\rho(x, z, y) = f(x) + g(z) &+ y^\intercal(Ax + Bz - c)
+ \frac{1}{2}\rho \| Ax + Bz - c\|_2^2
\end{aligned}
- \(\rho > 0, \ \rho \in \R\) can be seen as a penalty parameter
- \(\|\cdot\|_2\) denotes the Euclidean norm
- \(y \in \R^l\) is a vector of dual variables
\begin{aligned}
\min \quad& f(x) + g(z) \\
\text{s.t.}
\quad & Ax + Bz = c
\end{aligned}
- Initialization: Choose initial guesses \(x^{(0)}\), \(z^{(0)}\), and \(y^{(0)}\).
- Iteration: For \(k = 0, 1, 2, \ldots\) until convergence, update:
\begin{aligned}
L_\rho(x, z, y) = f(x) + g(z) &+ y^\intercal(Ax + Bz - c)
+ \frac{1}{2}\rho \| Ax + Bz - c\|_2^2
\end{aligned}
\begin{aligned}
x^{(k+1)} & := \argmin_x L_\rho(x, z^{(k)}, y^{(k)}) \\
z^{(k+1)} & := \argmin_z L_\rho(x^{(k+1)}, z, y^{(k)}) \\
y^{(k+1)} & := y^{(k)} + \rho \left( Ax^{(k+1)} + Bz^{(k+1)} - c \right)
\end{aligned}
3. Convergence Check: Stop the iterations if the stopping criteria are satisfied.
ADMM Introduction (3/3)
Scaled price variables
2. Iteration: For \(k = 0, 1, 2, \ldots\) until convergence, update:
\begin{aligned}
L_\rho(x, z, u) =& f(x) + g(z) - (\rho/2) \|u\|_2^2
+ (\rho/2) \| Ax + Bz - c + u\|_2^2
\end{aligned}
\begin{aligned}
x^{(k+1)} & := \argmin_x f(x) + (\rho/2) \| Ax + Bz^{(k)} - c + u^{(k)}) \|_2^2 \\
z^{(k+1)} & := \argmin_z g(z) + (\rho/2) \| Ax^{(k+1)} + Bz - c + u^{(k)}) \|_2^2 \\
u^{(k+1)} & := u^{(k)} + Ax^{(k+1)} + Bz^{(k+1)} - c
\end{aligned}
- Introduce a scaled dual variable \( u:= (1/\rho) y\), and reformulate the Augmented Lagrangian (using completion of squares) as:
- Gives simpler update steps:
Example 1: Constrained Convex Optimization
- Put the problem into ADMM form:
\begin{aligned}
\min \quad& f(x) \\
\text{s.t.}
\quad & x \in \mathcal{C}
\end{aligned}
\begin{aligned}
\min \quad& f(x) + \tilde{I}_\mathcal{C}(z) \\
\text{s.t.}
\quad & x - z = 0
\end{aligned}
\iff
- Consider the problem:
- \( \mathcal{C} \subset \mathbb{R}^n \) a convex set
- \( f: \mathbb{R}^n \rightarrow \mathbb{R} \) a convex function
- \( \tilde{I}_\mathcal{C} \) indicator function for set \( \mathcal{C} \)
Example 1: Constrained Convex Optimization
\begin{aligned}
x^{(k+1)} & := \argmin_x \left( f(x) + (\rho/2) \| x - z^{(k)} + u^{(k)} \|_2^2 \right) \\
z^{(k+1)} & := \Pi_\mathcal{C}( x^{(k+1)} + u^{(k)}) \\
u^{(k+1)} & := u^{(k)} + x^{(k+1)} - z^{(k+1)}
\end{aligned}
Update steps now take the form:
\begin{aligned}
\min \quad& f(x) + \tilde{I}_\mathcal{C}(z) \\
\text{s.t.}
\quad & x - z = 0
\end{aligned}
- x-update is unconstrained convex optimization
- \( \Pi_\mathcal{C} \) is the Euclidean projection
- For many problems the z-update step has a closed-form solution!
\begin{aligned}
\min \quad& f(x) \\
\text{s.t.}
\quad & x \in \mathcal{C}
\end{aligned}
\iff
- Put the problem into ADMM form:
\iff
- Consider the problem:
- \( f_i: \mathbb{R}^n \rightarrow \mathbb{R} \) convex functions
- \( z \in \mathbb{R}^n \)
- \( x_i \in \mathbb{R}^n \) are "local copies" of \( z \)
Example 2: Global Variable Consensus
\begin{aligned}
\min \quad& \sum_{i=1}^N f_i(z)
\end{aligned}
\begin{aligned}
\min \quad& \sum_{i=1}^N f_i(x_i) \\
\text{s.t.}
\quad & x_i - z = 0, \quad i = 1, \ldots, N
\end{aligned}
Example 2: Global Variable Consensus
Update steps now take the form:
\begin{aligned}
x^{(k+1)}_i & := \argmin_{x_i} \left( f_i(x_i) + (\rho/2) \| x_i - z^{(k)} + u^{(k)} \|_2^2 \right) \\
z^{(k+1)} & := \frac{1}{N} \sum^N_{i=1} (x_i^{(k+1)} + u^{(k)}_i ) \\
u^{(k+1)}_i & := u^{(k)}_i + x_i^{(k+1)} - z_i^{(k+1)}
\end{aligned}
- x-update is unconstrained convex optimization
- x-update can be solved in parallel
- y- and z-updates are very cheap
\iff
\begin{aligned}
\min \quad& \sum_{i=1}^N f_i(z)
\end{aligned}
\begin{aligned}
\min \quad& \sum_{i=1}^N f_i(x_i) \\
\text{s.t.}
\quad & x_i - z = 0, \quad i = 1, \ldots, N
\end{aligned}
Two paths:
Solving GCS with ADMM
- Solve the non-convex SPP in GCS problem directly
- Solve the convex relaxation
1. Solve the non-convex problem directly
\newcommand{\set}[1]{\left\{#1\right\}}
\begin{aligned}
\min \quad& \sum_{e := (u,v) \in \mathcal{E}} y_e l_e(x_u, x_v) \\
\text{s.t.}
\quad & x_v \in \mathcal{X}_v, \quad \forall v \in \mathcal{V} \\
\quad & \sum_{e \in \mathcal{E}_v^\text{in}} y_e + \delta_{sv} =
\sum_{e \in \mathcal{E}_v^\text{in}} y_e + \delta_{tv} \leq 1, \quad \forall v \in \mathcal{V} - \set{s,t} \\
\quad & y_e \in \set{0,1} \quad \forall e \in \mathcal{E}
\end{aligned}
- Non-convex (naive) formulation of SPP in GCS:
- Bi-convex in \( y_e \) and \( x_v \) (except for integrality on \( y_e \) )
- Let us use ADMM to decompose the problem
1. Solve the non-convex problem directly
- Use the "global variable consensus" trick and decompose over edges
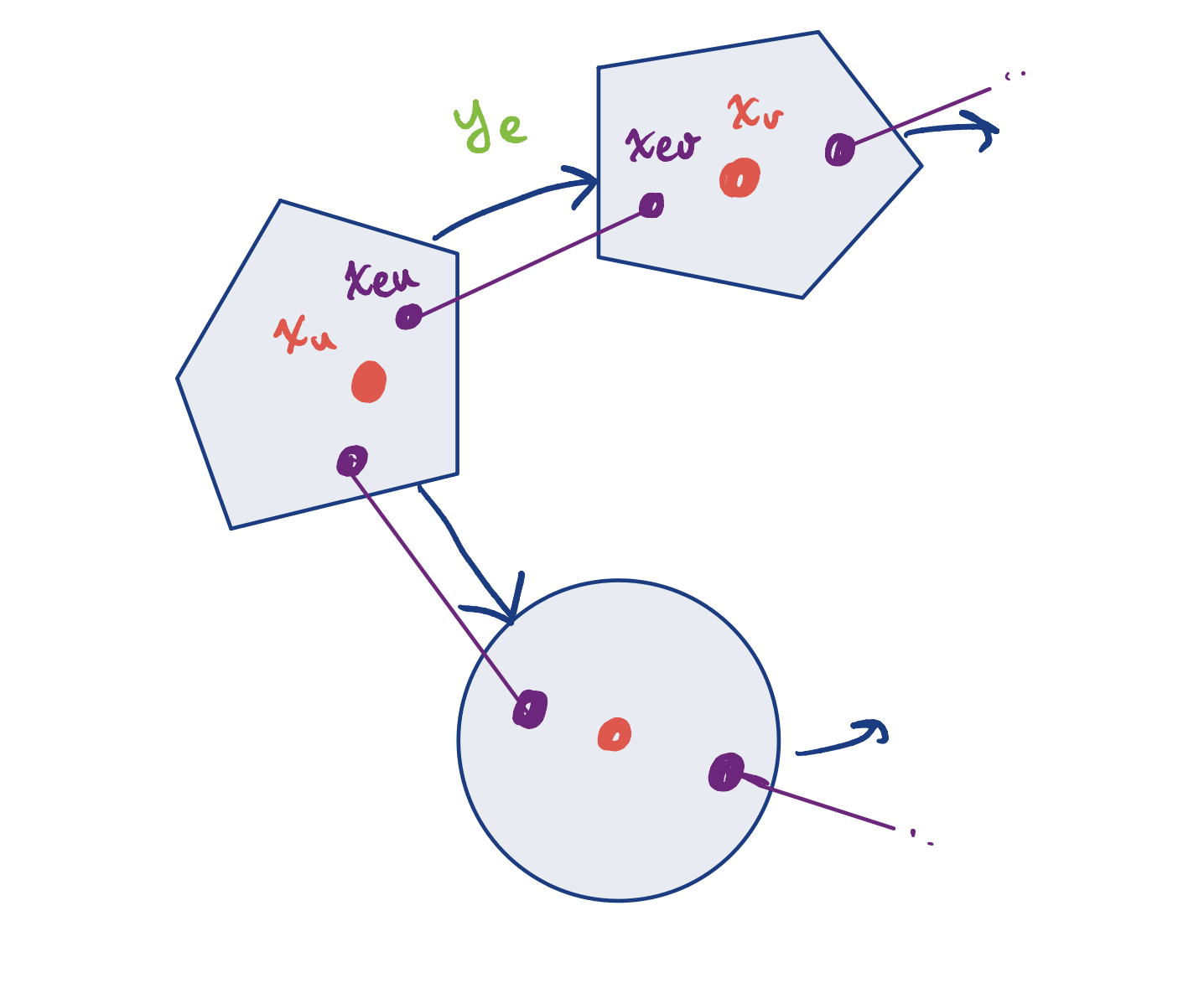
- Introduce auxiliary variables ("local variables") for each edge:
- \(\forall e = (u, v)\) introduce the local variables \(x_{eu}\) and \(x_{ev}\).
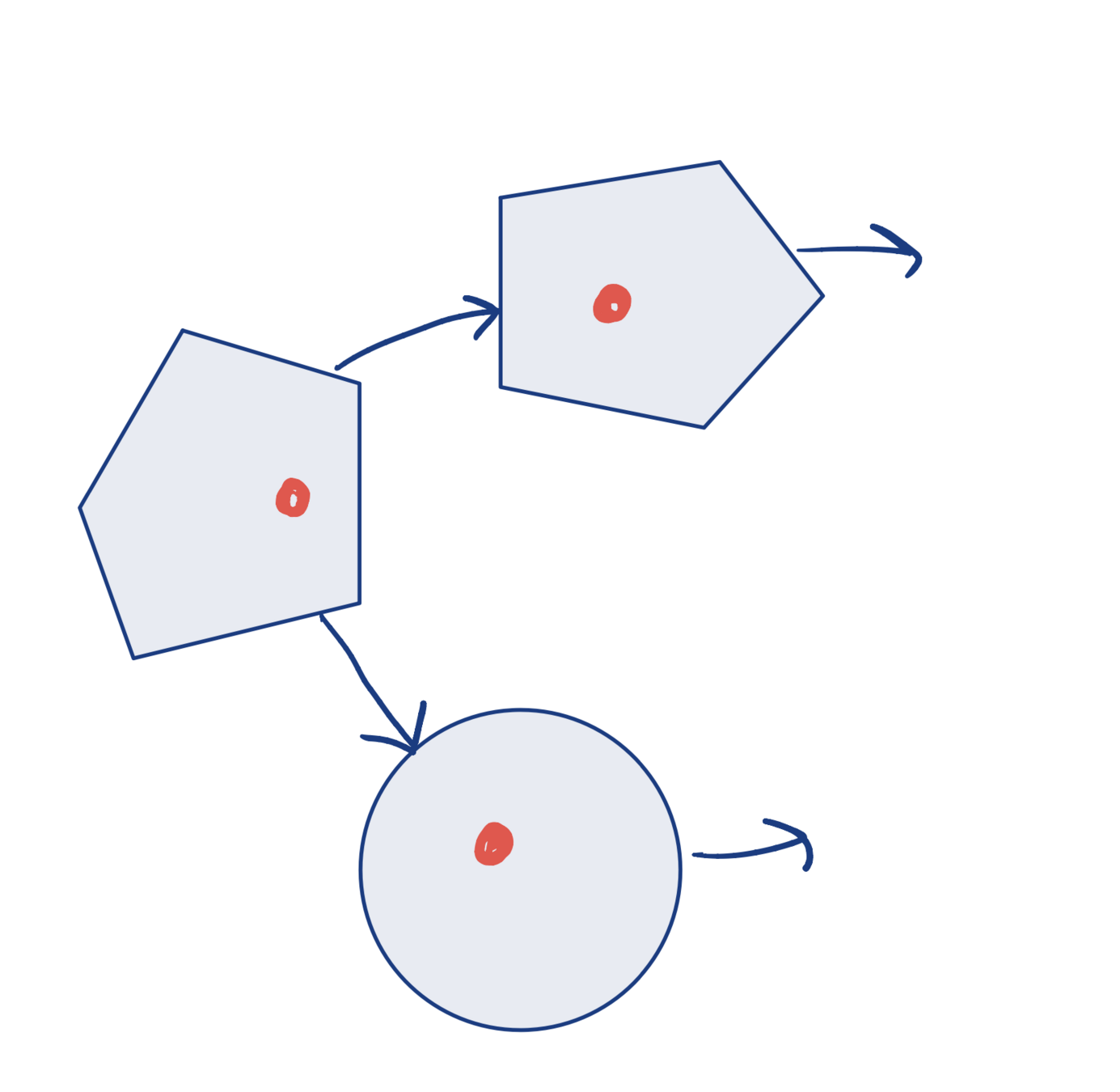
\( \longrightarrow \)
Original
With local copies
- Add "consensus constraint" for each edge:
1. Solve the MICP directly
\newcommand{\set}[1]{\left\{#1\right\}}
\begin{aligned}
\quad & x_{eu} - x_u = 0, \\
\quad & x_{ev} - x_v = 0, \quad \forall e = (u,v) \in \mathcal{E} \\
\end{aligned}
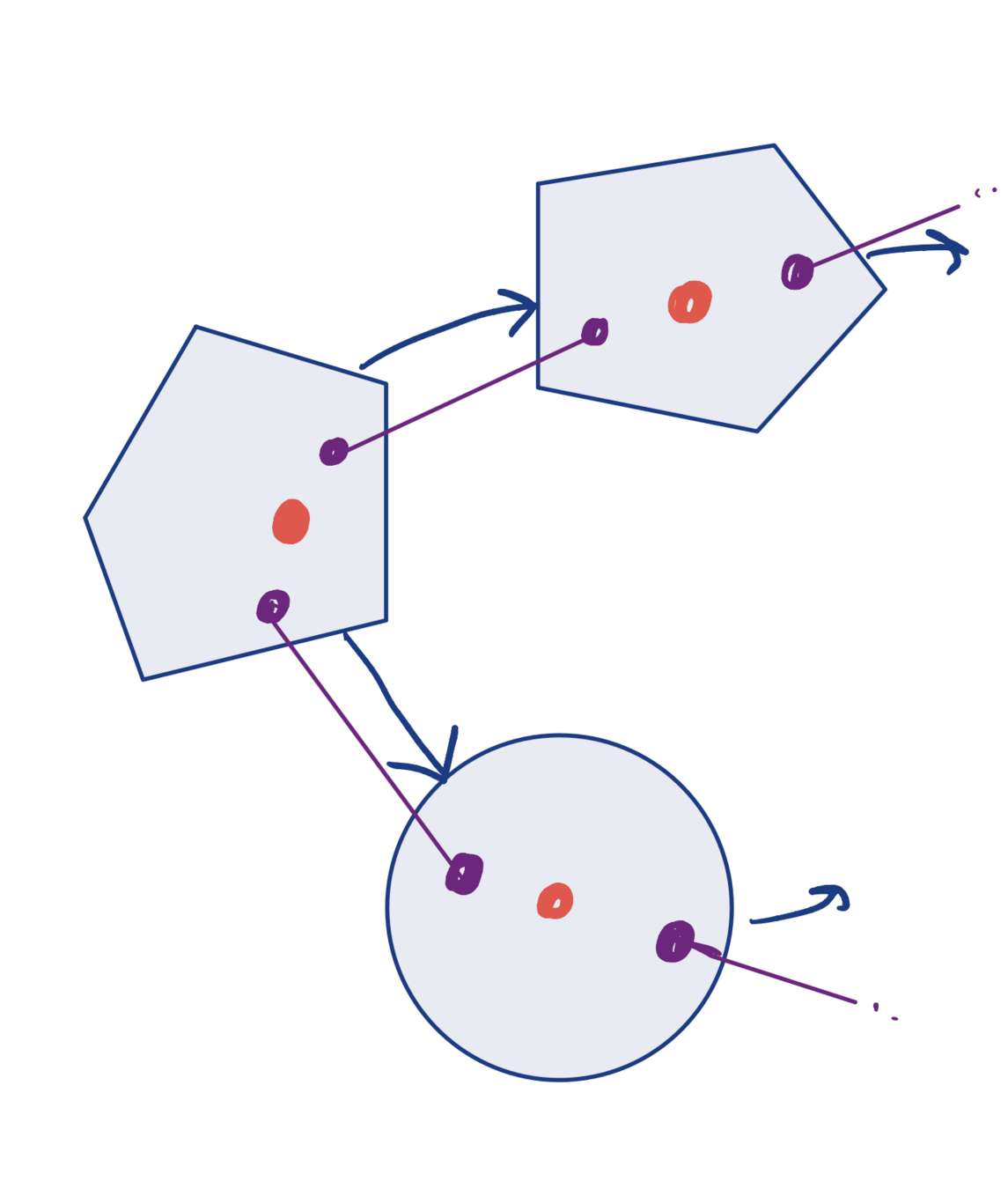
- Perform consensus over vertices
- Relax the consensus constraints into the Augmented Lagrangian
- Use the indicator function for all other constraints (keep them)
\( \longrightarrow \)
\newcommand{\set}[1]{\left\{#1\right\}}
\begin{aligned}
\min \quad& \sum_{e := (u,v) \in \mathcal{E}} y_e l_e(x_{eu}, x_{ev}) \\
\text{s.t.}
\quad & x_{eu} \in \mathcal{X}_u, \; x_{ev} \in \mathcal{X}_v, \\
\quad & x_{eu} - x_u = 0, \\
\quad & x_{ev} - x_v = 0, \quad \forall e = (u,v) \in \mathcal{E} \\
\quad & \sum_{e \in \mathcal{E}_v^\text{in}} y_e + \delta_{sv} =
\sum_{e \in \mathcal{E}_v^\text{in}} y_e + \delta_{tv} \leq 1, \quad \forall v \in \mathcal{V} - \set{s,t} \\
\quad & y_e \in \set{0,1} \quad \forall e \in \mathcal{E}
\end{aligned}
- For each edge \(e = (u, v)\) introduce the local variables \(x_{eu}\) and \(x_{ev}\). We can now rewrite the SPP GCS problem as:
"Consensus constraints"
\( \leftarrow \)
Cost now decomposes independently over edges
\( \leftarrow \)
1. Solve the MICP directly
1. Solve the MICP directly
We now have three blocks of variables:
- Consensus variables: \( x_v, \, v \in \mathcal{V} \)
- Local variables: \((x_{eu}, x_{ev}), \, e = (u,v) \in \mathcal{E} \)
- Flow variables: \( y_e, \, e \in \mathcal{E} \)
The problem is bi-convex in these
1. Solve the MICP directly
-
Local update: Solve a small shortest path problem between two vertices
- Can be solved in parallel
- Consensus update: Closed-form mean:
\begin{aligned}
x_{v}^{(k+1)} :=
\frac{1}{ | \mathcal{E}_v | }
\sum_{e \in \mathcal{E}_v}
\left(
x_{ev}^{(k+1)}
+ \lambda_{ev}^{(k)}
\right)
\end{aligned}
3. Discrete update: Reduces to a discrete SPP (solve with Dijkstra)
\begin{aligned}
\lambda^{(k+1)}_{eu} & := \lambda^{(k)}_{eu} + x_{eu} - x_u
\end{aligned}
\begin{aligned}
\lambda^{(k+1)}_{ev} & := \lambda^{(k)}_{ev} + x_{ev} - x_v
\end{aligned}
4. Dual update:
- Simple problems
- Expect convergence issues on harder instances
- Still, the "global" decision of which path to take is changing several times!
\newcommand{\set}[1]{\left\{#1\right\}}
\begin{aligned}
\min &\quad \sum_{e \in \mathcal{E}} \tilde{l}_e(z_e, z_e', y_e) \\
\text{s.t.}
\quad & \sum_{e\in \mathcal{E}^\text{out}_s} y_e = 1,
\sum_{e\in \mathcal{E}^\text{in}_t} y_e = 1 \\
\quad & \sum_{e\in \mathcal{E}^\text{in}_v} y_e \leq 1, \quad \forall v \in \mathcal{V} - \set{s,t} \\
\quad & \sum_{e\in \mathcal{E}^\text{in}_v} (z_e', y_e) =
\sum_{e\in \mathcal{E}^\text{out}_v} (z_e, y_e)
\quad \forall v \in \mathcal{V} - \set{s,t} \\
\quad & (z_e,y_e) \in \tilde{\mathcal{X}}_u \\
\quad & (z_e',y_e) \in \tilde{\mathcal{X}}_v,
\quad \forall e = (u,v) \in \mathcal{E}
\end{aligned}
2. Solve the convex relaxation
- Convex relaxation of GCS problem:
- \( z_e \) spatial flow in for edge \( e \)
- \( z_e' \) spatial flow out for edge \(e \)
- \( y_e \) flow for edge \(e \)
2. Solve the convex relaxation
- To make the cost terms and all constraints independent, we now decompose over vertices
- For each vertex, introduce local variables
- Do consensus over edges
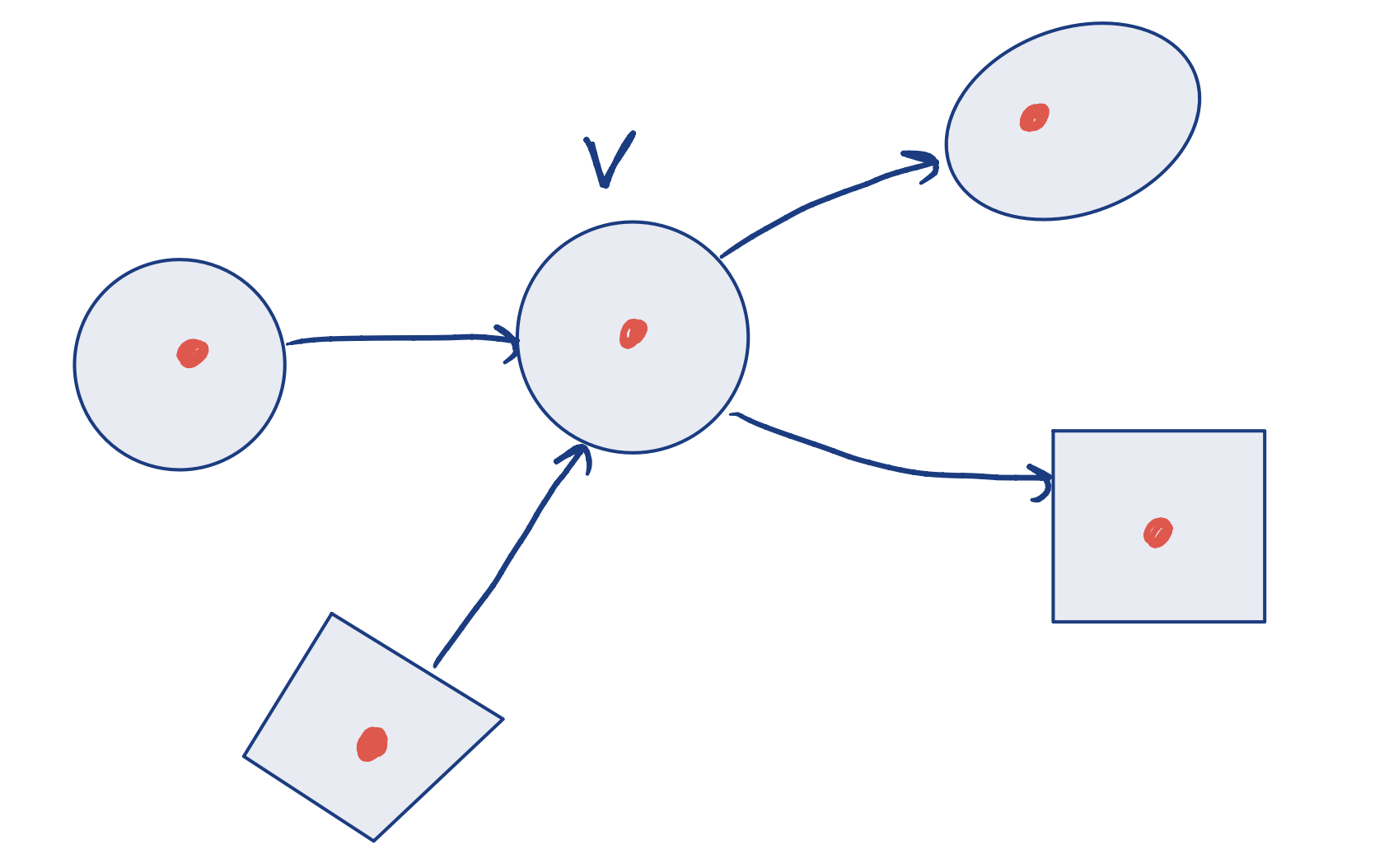
Original
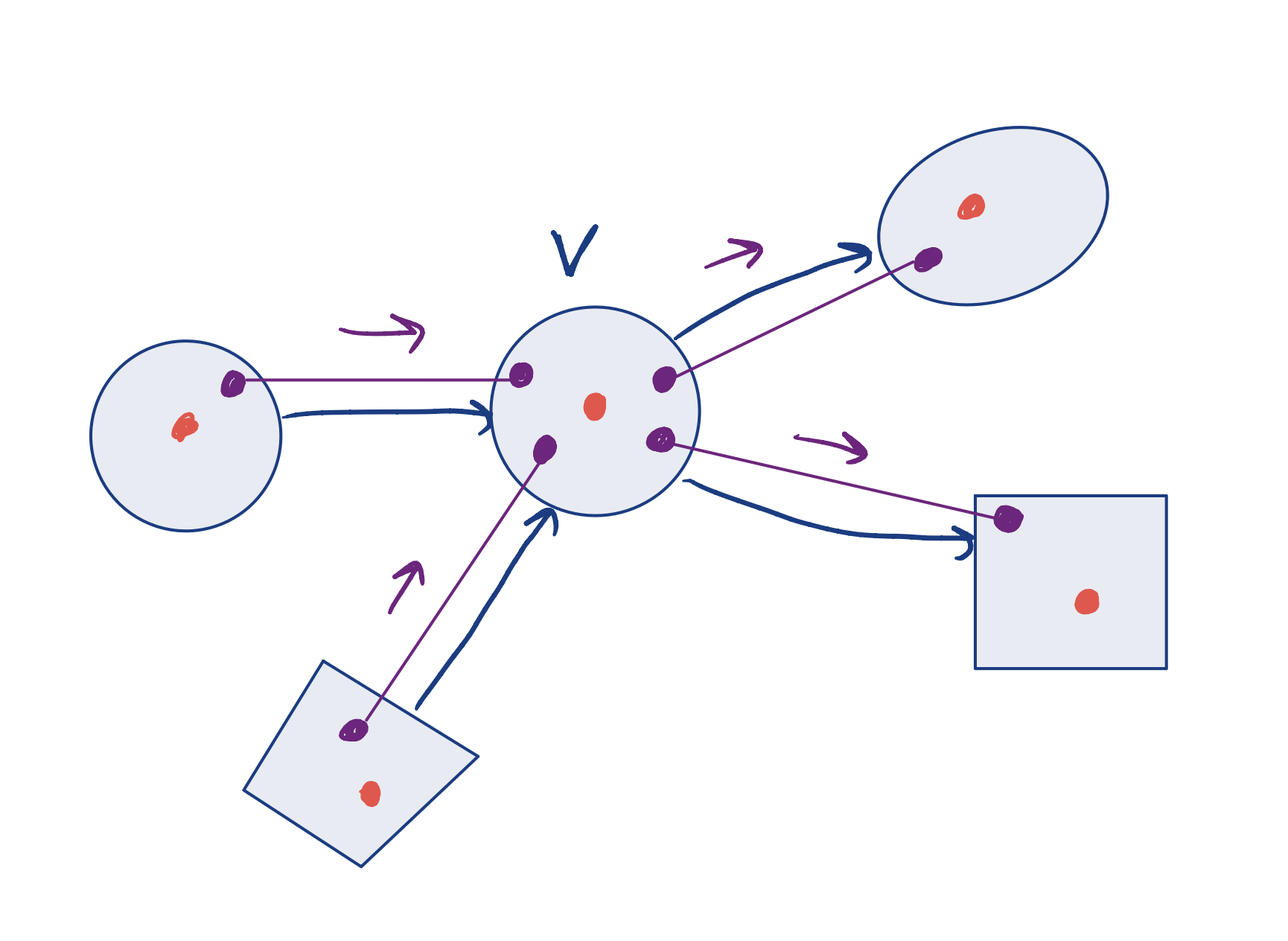
With local copies
\( \longrightarrow \)
2. Solve the convex relaxation
We now have two blocks of variables:
- Local variables (over vertices): \( z_{ve}, z_{ve}', y_{ve}, \, \forall v \in \mathcal{V}, \forall e \in \mathcal{E}_v\).
- Consensus variables (over edges): \((z_{e}, z_{e}', y_e), \, \forall e \in \mathcal{E} \)
2. Solve the convex relaxation
-
Local update (on vertices): For each vertex, solve a small SOCP with neighboring vertices
- Can be solved in parallel
3. Dual update:
\begin{aligned}
z_e^{(k+1)} &:=
(1/2) (z_{ue}^{(k+1)} + \lambda_{ue}^{(k+1)} +
z_{we}^{(k+1)} + \lambda_{we}^{(k+1)}) \\
y_e^{(k+1)} &:=
(1/2) (y_{ue}^{(k+1)} + \mu_{ue}^{(k+1)} +
y_{we}^{(k+1)} + \mu_{we}^{(k+1)}) \\
\end{aligned}
\begin{aligned}
\lambda^{(k+1)}_{ve} & := \lambda^{(k)}_{ve} + z_{ve}^{(k+1)} - z_e^{(k+1)} \\
\mu^{(k+1)}_{ve} & := \mu^{(k)}_{ve} + y_{ve}^{(k+1)} - z_e^{(k+1)} \\
\end{aligned}
2. Consensus update (on edges): For each edge, compute the consensus variables as "the mean" over the local edge variables:
First result
- Not very fast, but converges
- Each iteration only relies on local information (neighboring vertices and edges)
Green = GCS solution
Red = ADMM solution
Conclusion
- Very preliminary work, but seems interesting
- Maybe this can be a way to remove "irrelevant" parts of the problem?
- For instance: Only solve subproblems where incoming flow is non-zero
- Need to clearly define what problems that would benefit from being solved like this