Optimization-based Planning Through Contact with Tight Convex Relaxations 

1X Robotics, August 2023

Bernhard Paus Græsdal

Robot Locomotion Group, MIT

About me

  • Current PhD student at RLG, MIT
  • MsC in Cybernetics and Robotics from NTNU
  • Research: Planning Through Contact with Convex Optimization

Robot Locomotion Group

  • Led by Prof. Russ Tedrake
  • Focused on robot locomotion for many years
  • Tools from optimization, control and machine learning
  • Today focused on Robotic Manipulation
  • Lmk if you want to visit!

Planning Through Contact

Dexterous Manipulation: How to pick up the book?

Planning Through Contact

Complex planning problem:

  • 4 contact bodies
    (table, book, two fingers)
  • 4 different contact modes
  • Both pushing and sticking
  • Collision-free motion planning

Dexterous Manipulation: How to pick up the book?

How are these problems solved today?

Task-specific hardware

\( \rightarrow \) Not dexterous manipulation

How are these problems solved?

Learning-based methods

\( \rightarrow \) Hard to generalize

  • Sampling-based
  • Task-and-Motion-Planning (TAMP)
    (often sampling-based)
  • Multi-Modal Motion Planning (MMMP)

Planning algorithms:

How are these problems solved?

[1] T. Pang, H. J. T. Suh, L. Yang, and R. Tedrake, “Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models.” arXiv, Jun. 21, 2022

[1]

\( \rightarrow \) Several pros and cons

\( \rightarrow \) No known (general) satisfactory solution

Our goal

  • Optimization-based planner for dexterous manipulation
  • Plan both discrete contact mode sequence and continuous motion simultaneously

\(\leftarrow\) Toy-problem we will tackle

Preliminary results: Planar Pushing

Technical Approach

Characteristics of the problem:

  • Hybrid system
  • Nonlinear kinematics and dynamics
  • (we use planar pushing here as an example; generalizes to general rigid body dexterous manipulation!)

Technical Approach

  • Hybridness
    • Solve using convex (linear) Mixed-Integer relaxations
  • Nonlinearities
    • Solve using convex (semidefinite) programming relaxations
  • We propose to use convex optimization and tight convex relaxations to solve the problem!

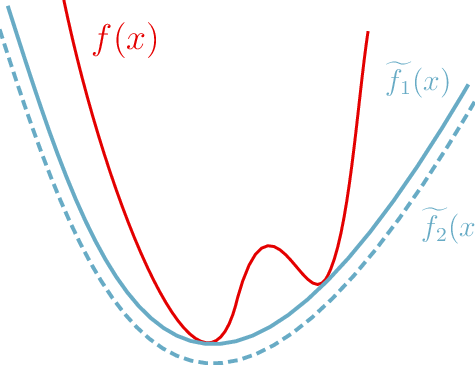
\( \tilde{f}_1 \) and \(\tilde{f}_2\) are simple examples of convex relaxations

1. Hybridness of the problem

  • Combinatorial problems can be solved with MICP
    • (generally) NP-hard
  • Formulate the problem as
    Graph-of-Convex-Sets (GCS) problem
    • 1. Efficient encoding, fewer integer variables
    • 2. Tight convex relaxation
      \( \rightarrow \)       we can solve it fast!
    • (Round to obtain true solution)

[2] T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” arXiv, Sep. 21, 2022.

[3] T. Marcucci, M. Petersen, D. von Wrangel, and R. Tedrake, “Motion Planning around Obstacles with Convex Optimization.” arXiv, May 09, 2022.

[2]

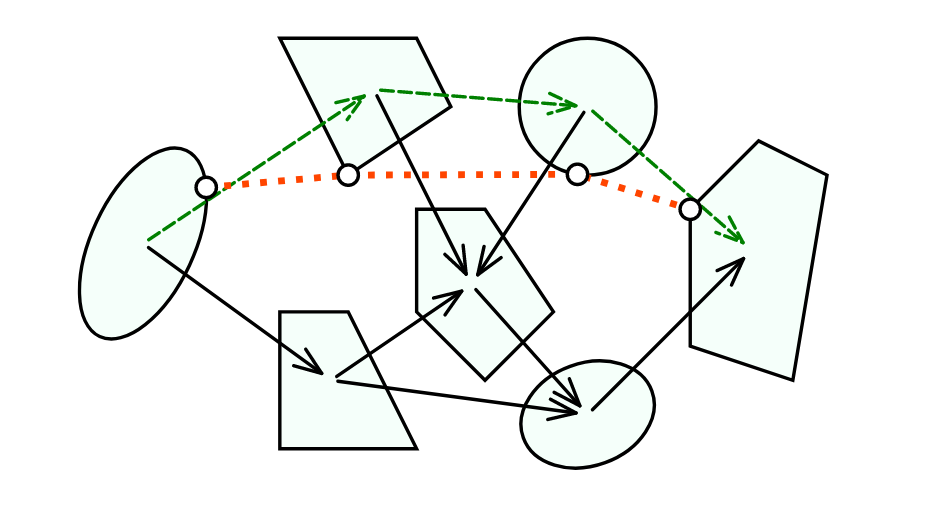
Graph of Convex Sets (GCS)

[2] T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” arXiv, Sep. 21, 2022.

[3] T. Marcucci, M. Petersen, D. von Wrangel, and R. Tedrake, “Motion Planning around Obstacles with Convex Optimization.” arXiv, May 09, 2022.

[2]

TODO add Mark video!

Graph-of-Convex-Sets

  • Directed graph \( G = (\mathcal{V}, \mathcal{E}) \)
  • Bounded convex sets \( \mathcal{X}_v \)
  • Source and target \( \sigma, \tau \in \mathcal{V} \)
  • \( \mathcal{P} \) family of all \( \sigma-\tau \) paths in \( G \)
  • \( \mathcal{E}_p \) set of edges traversed by path \( p \in P \)
  • Convex edge lengths \( l_e(x_u, x_v) \geq 0 \)
  • Convex edge constraints \( \mathcal{X}_e \)
\begin{aligned} \min \quad& \sum_{e := (u,v) \in \mathcal{E}_p} l_e(x_u, x_v) \\ \text{s.t.} \quad& p \in \mathcal{P}, \\ \quad & x_v \in \mathcal{X}_v, \quad \forall x_v \in p, \\ \quad & (x_u, x_v) \in \mathcal{X}_e, \quad \forall e := (x_u, x_v) \in \mathcal{E}_p \end{aligned}

[1] T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” 2022.

[2] T. Marcucci, M. Petersen, D. von Wrangel, and R. Tedrake, “Motion Planning around Obstacles with Convex Optimization.” 2022.

2. Handling nonlinearities

  • Constraints are polynomial
  • Problem can be formulated as a (non-convex) QCQP
  • Can be relaxed to a Semidefinite Program (SDP)
    • Convex and can be solved efficiently!
    • (round to obtain true solution)

2. Handling nonlinearities

\begin{aligned} \min_{x} \quad x^\intercal Q_0 x & \\ \text{subject to} \quad x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\ \quad Ax &\geq 0 \\ \quad x &= \begin{bmatrix} 1 \\ y \end{bmatrix} \end{aligned}
  • A general non-convex QCQP:
  • (any polynomial problem can be put in this form)

2. Handling nonlinearities

\begin{aligned} \min_{x} \quad x^\intercal Q_0 x & \\ \text{subject to} \quad x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\ \quad Ax &\geq 0 \\ \quad x &= \begin{bmatrix} 1 \\ y \end{bmatrix} \end{aligned}
  • We solve it with the standard SDP relaxation
\begin{aligned} \min_{x} \quad \langle Q_0, X \rangle & \\ \text{subject to} \quad \langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\ \quad AXA^\intercal &\geq 0 \\ \quad AXe_1^\intercal &\geq 0 \\ \quad e_1^\intercal X e_1 &= 1 \\ \quad X \succeq 0 \\ \end{aligned}

\( \longrightarrow \)

  • Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
  • (This includes the McCormick envelopes/outer-approximation of bilinear constraints)

\( X := xx^\intercal \)

2. Handling nonlinearities

  • Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
    • Usually not the case
    • Relaxation close to being tight
    • Round using nonlinear trajopt and fixed mode-sequence

Hope: Convex relaxation contains enough information to take the right high-level decisions

Seems to be the case!

Preliminary Results

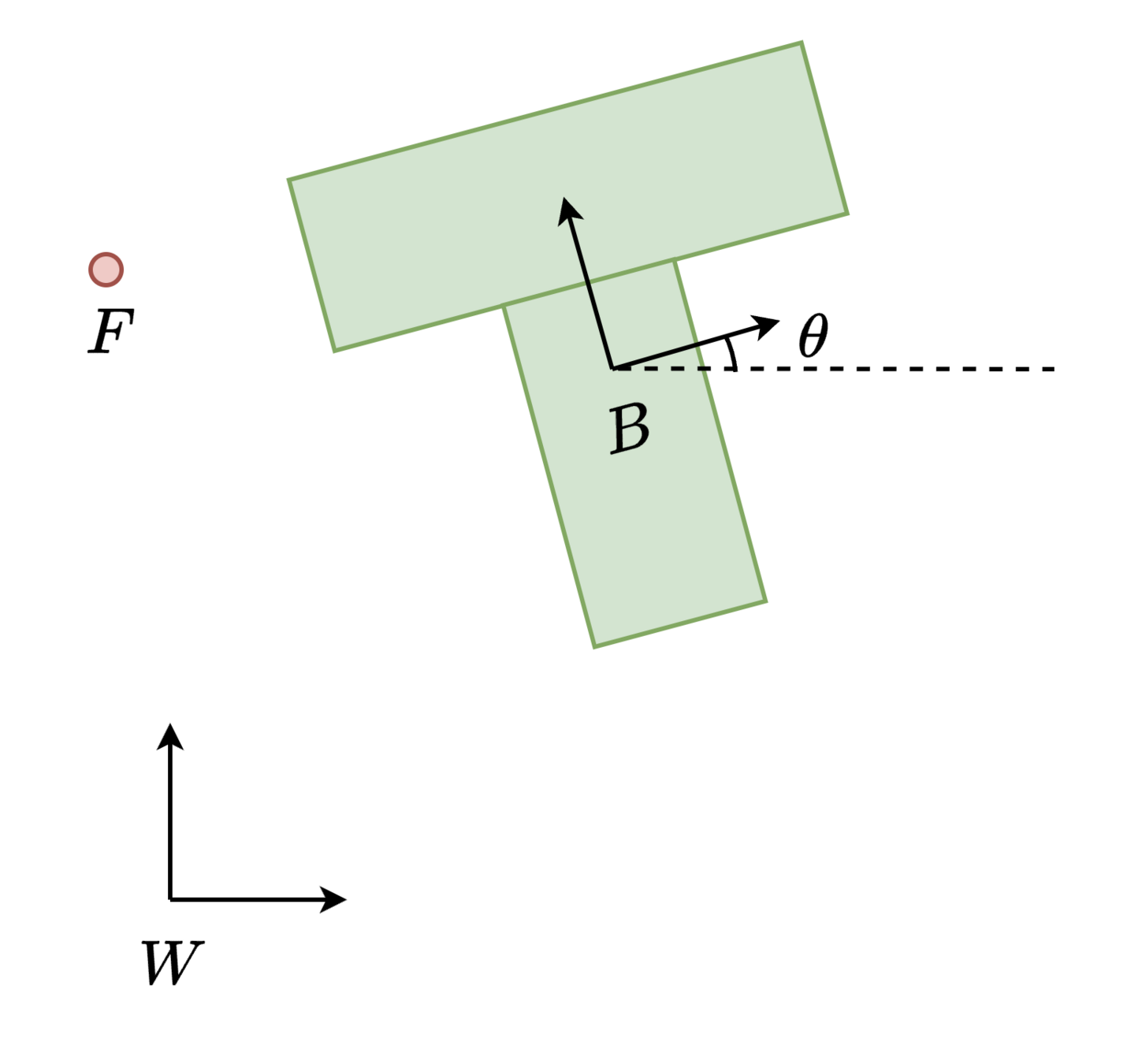
Pushing for the T-object

General 2D dexterous manipulation

  • The method generalizes to general dexterous manipulation!

Future work

  • Pushing for ICRA 2023 with paper on complete motion planning for planar pushing
  • Execute trajectories on the real robot (with hybrid MPC as controller)
  • General 3D dexterous manipulation for general rigid objects

Thank you!