Planning Through Contact with Graphs of Convex Sets and Semidefinite Relaxations

Bernhard Paus Græsdal

Robot Locomotion Group, MIT

 

1X Robotics

August 11th 2023

About me

  • Current PhD student at RLG, MIT
  • Research: Planning Through Contact with Convex Optimization

Bernhard Paus Græsdal

Robot Locomotion Group

  • Led by Prof. Russ Tedrake
  • Focused on robot locomotion for many years
  • Tools from optimization, control and machine learning
  • ~20% of former members now work for BD
  • Today focused on Robotic Manipulation
  • Lmk if you want to visit!

Planning and control for complex robotic systems

A big focus for the group:

Goal: Deeper connections between

Trajectory optimization

Sample-based planning

AI-style logical planning

Combinatorial optimization

Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.

Available at: https://arxiv.org/abs/2101.11565

Motion Planning around Obstacles with Convex Optimization.

Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.

Available at: https://arxiv.org/abs/2205.04422​

Simple example: Shortest path around an obstacle

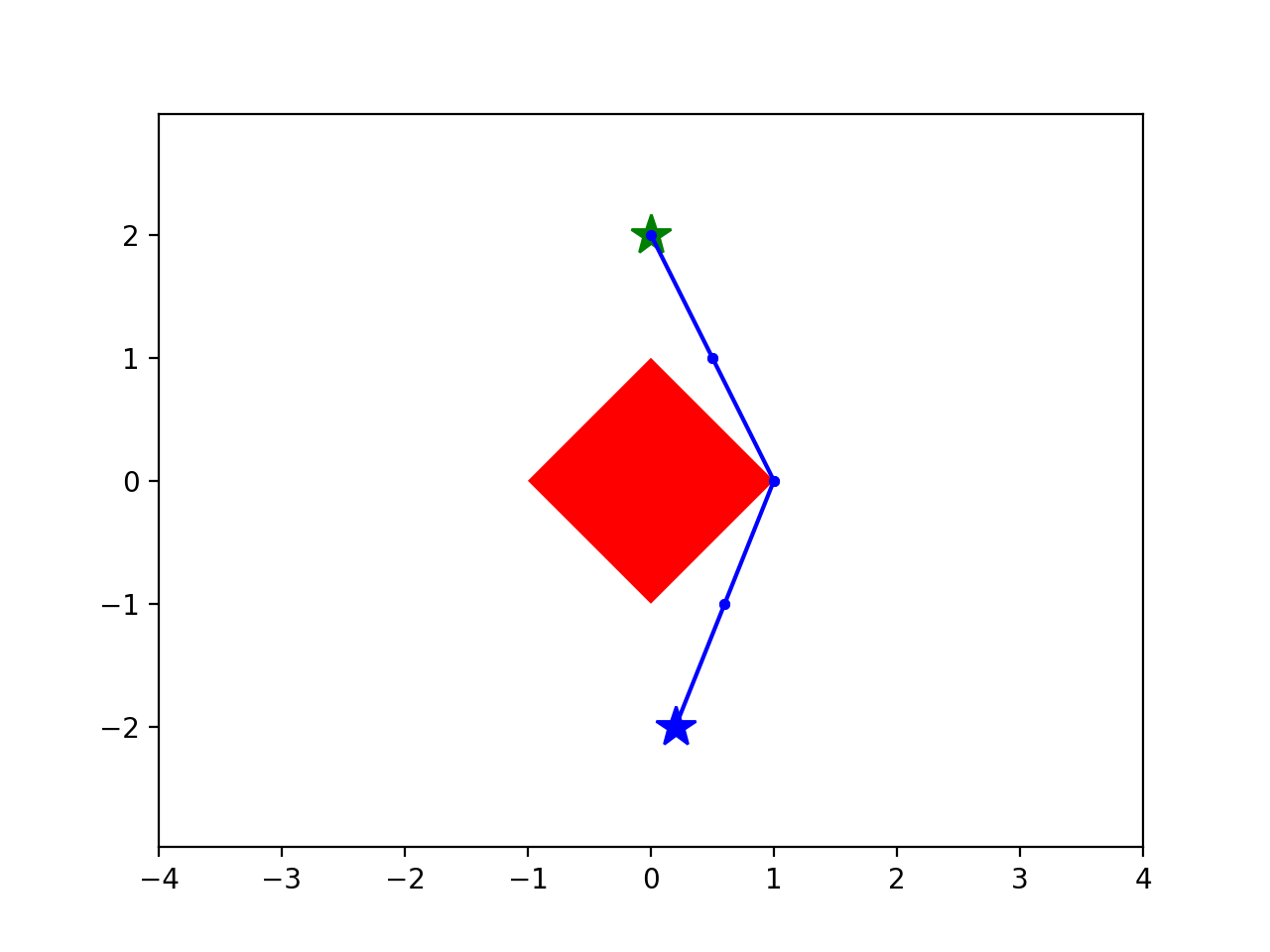
start

goal

  1. Combinatorial (e.g. over homotopy classes)
  2. Smooth optimization (over curves)

Two aspects of the motion planning problem:

start

goal

  • How to do trajectory optimization through the maze?

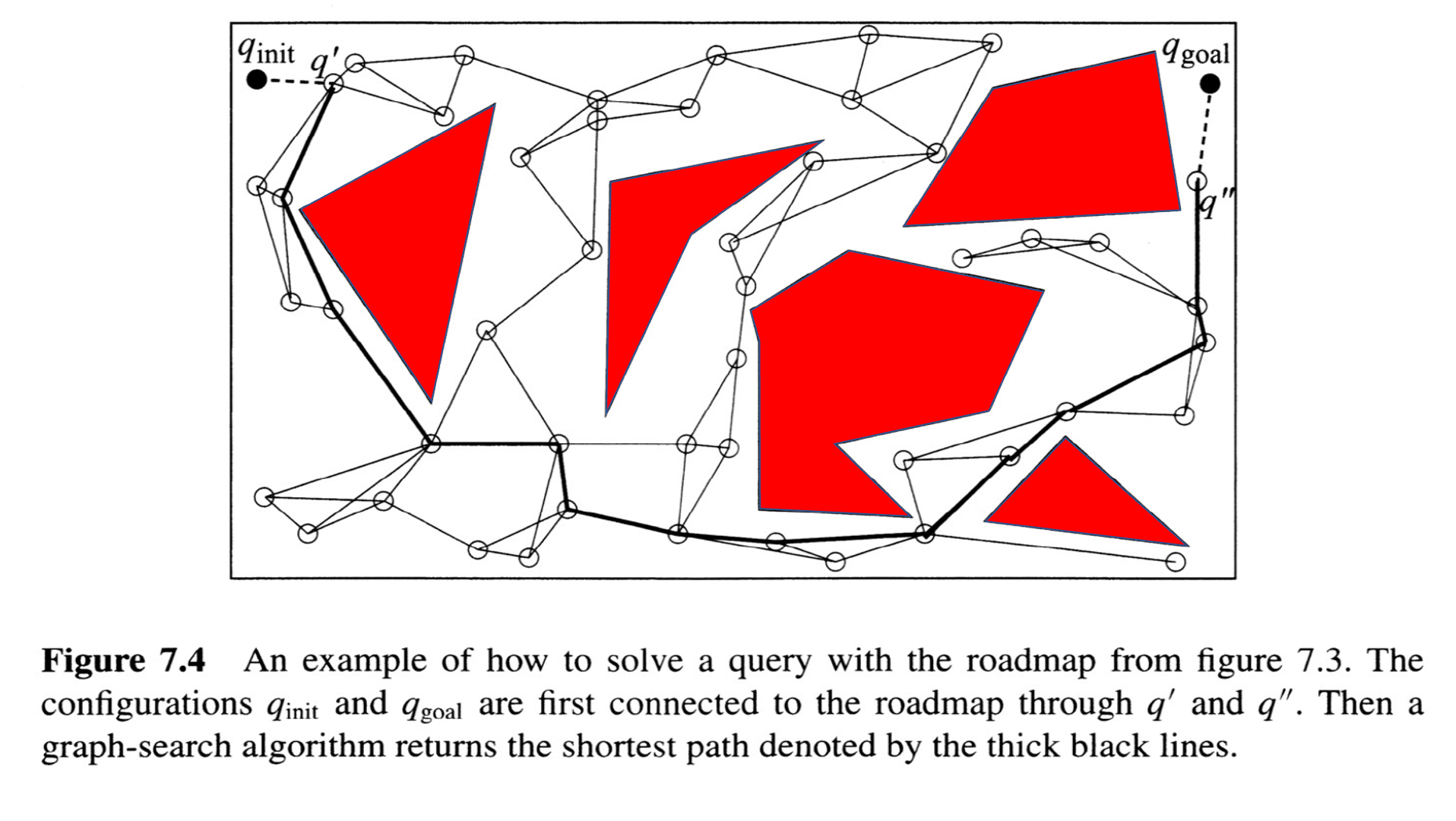
1. Combinatorial: Sampling-based motion planning

The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.

2. Smooth: Trajectory Optimization

  • Vertices \(V\)
  • (Directed) edges \(E\)

Combining Graph Search + Trajectory Optimization

  • Start with classical Linear Programming (LP) formulation of SPP

Graphs of Convex Sets

 

  • For each \(i \in V:\)
    • Compact convex set \(X_i \subset \R^d\)
    • A point \(x_i \in X_i \) 
  • Edge length given by a convex function \[ \ell(x_i, x_j) \]

Note: The blue regions are not obstacles.

New shortest path formulation

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

Classic shortest path LP

\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\ \mathrm{s.t.} \quad & x_i \in X_i, && \forall i \in V, \\ & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si} \le 1, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

now w/ Convex Sets

Example: "Footstep planning" with \(x_{n+1}=Ax_n + Bu_n\)

Formulating motion planning with differential constraints as a Graph of Convex Sets (GCS)

+ time-rescaling

Motion Planning Results

minimum distance

minimum time

Back to the maze example...

Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.

Scaling

  • ~10k regions in 3D
     
  • 20k vertices and 400k edges.
     
  • Online planning takes 0.3s

by Tobia Marcucci in collaboration w/ Stephen Boyd

Going beyond collision-free motion planning...

How to pick up the book?

Planning Through Contact

  • 4 contact bodies
    (table, book, two fingers)
  • Many different contact modes
  • Both sliding and sticking
  • Collision-free motion planning

Complex planning problem:

How to push the object?

Planning Through Contact

C. Chi et al., “Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.” arXiv, Mar. 09, 2023

  • No satisfactory planning algorithm for this problem!

Characteristics of the problem:

  • Hybrid system
  • Nonlinear kinematics and dynamics

Using GCS for Planning Through Contact

\(\rightarrow \) Solve hybridness by using GCS

Nonlinearities and convex relaxations

  • Solve nonlinearities by using convex (semidefinite) programming relaxations 
  • We propose to use convex optimization and tight convex relaxations to solve the problem!

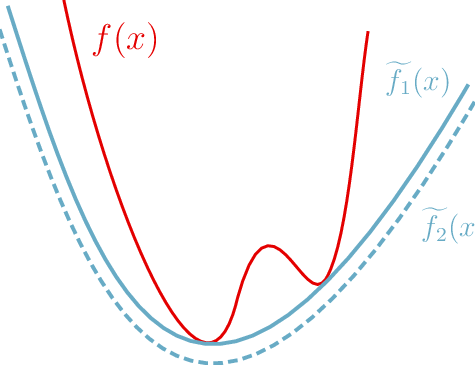
\( \tilde{f}_1 \) and \(\tilde{f}_2\) are simple examples of convex relaxations

\begin{aligned} \min_{x} \quad x^\intercal Q_0 x & \\ \text{subject to} \quad x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\ \quad Ax &\geq 0 \\ \quad x &= \begin{bmatrix} 1 \\ y \end{bmatrix} \end{aligned}
  • A general non-convex QCQP:
  • (any polynomial problem can be put in this form)

Formulate the problem as a QCQP

  • (any polynomial problem can be put in this form)

Non-convex when \( Q_i \preceq 0 \)

\begin{aligned} \min_{x} \quad x^\intercal Q_0 x & \\ \text{subject to} \quad x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\ \quad Ax &\geq 0 \\ \quad x &= \begin{bmatrix} 1 \\ y \end{bmatrix} \end{aligned}
\begin{aligned} \min_{x} \quad \langle Q_0, X \rangle & \\ \text{subject to} \quad \langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\ \quad AXA^\intercal &\geq 0 \\ \quad AXe_1^\intercal &\geq 0 \\ \quad e_1^\intercal X e_1 &= 1 \\ \quad X \succeq 0 \\ \end{aligned}

\( \longrightarrow \)

  • Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
  • (This includes the McCormick envelopes/outer-approximation of bilinear constraints)

\( X := xx^\intercal \)

Solve it using Semidefinite Programming (SDP)

  • Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \) \( \rightarrow\) relaxation is "tight"
    • In general not the case (otherwise \( P = NP \) )
    • Depending on the problem, relaxation can be tight
  • Hope: Convex relaxation contains enough information to take the correct high-level decisions
  • Then we can refine the details as a final step!

Retrieve the solution

Preliminary results on using GCS and Semidefinite relaxations for planning through contact...

Planning through contact for Planar Pushing

Planning through contact for general manipulation

  • Pushing for ICRA 2023 with paper on first results
  • Next step: General 3D dexterous manipulation for general rigid objects

Future work

Thank you!