Contact-rich planning without mode enumeration

Short Talk, RLG MIT

February 23rd 2024

Bernhard Paus Graesdal

Preliminary work:

Motivation

  • Use GCS for contact-rich planning
  • Currently contact modes are encoded explicitly in graph
  • An obstacle is scaling
  • Contact mode enumeration scales exponentially with number of bodies in a scene

Example

  • A box on a table with a point finger
  • We model three contact points:
  • Table and box bottom left corner, Table and box bottom right corner, finger and box left face
  • Consider 4 modes:
  • Non-contact, sticking contact, sliding left, sliding right
  • We get \(4^3 = 64\) modes = vertices in GCS
  • Need \(64^2 = 4096\) edges to model arbitrary contact mode transitions!

Proposed solution

  1. Describe contact modes implicitly using Linear Complimentarity Constraints (LCPs)
  2. LCPs can be encoded as linear inequality and quadratic equality constraints
  3. Use Semidefinite Relaxations to relax the feasible set
  4. Solve a convex program to obtain a lower bound/relaxed solution
  5. Round to obtain feasible solution

Complimentarity Constraints

  • Contact modes can be encoded as Complimentarity Constraints:
    \( 0 \leq f(x) \perp g(x) \geq 0, \quad f, g: \R^n \rightarrow \R^n \)
  • Nonnegativity implies that this must hold element-wise
  • Only one expression can be positive at a time:
    • \( f_i(x) = 0 \) and \( g_i(x) \geq 0 \)
    • \( f_i(x) \geq 0 \) and \( g_i(x) = 0 \)
  • We obtain an LCP when \(f\) and \(g\) are linear:
    \( 0 \leq Ax + b \perp Cx + d \geq 0 \)
  • Which we can encode with linear and quadratic constraints
     

Example: Contact/Non-contact

  • Two modes: Contact or non-contact
  • Let \( \phi : \R^n \rightarrow \R\) be SDF and let \( \lambda_n \in \R \) be normal force
  • Contact: \(\phi(q) = 0 \) and \(\lambda_n \geq 0\)
  • Non-contact: \(\phi(q) \geq 0 \) and \(\lambda_n = 0\)

Example: Contact/Non-contact

0 \leq \phi(q) \perp \lambda_n \geq 0
  • Suppose \(\phi\) is linear (i.e. by approximation)
  • Then the LCP is obviously:

Example: Sliding/Sticking

  • Two modes: Sliding or Sticking (in 2D)
  • \( \lambda_f \in \R \) is the friction force, \( v_{\text{rel}} \in \R \) is the relative sliding velocity

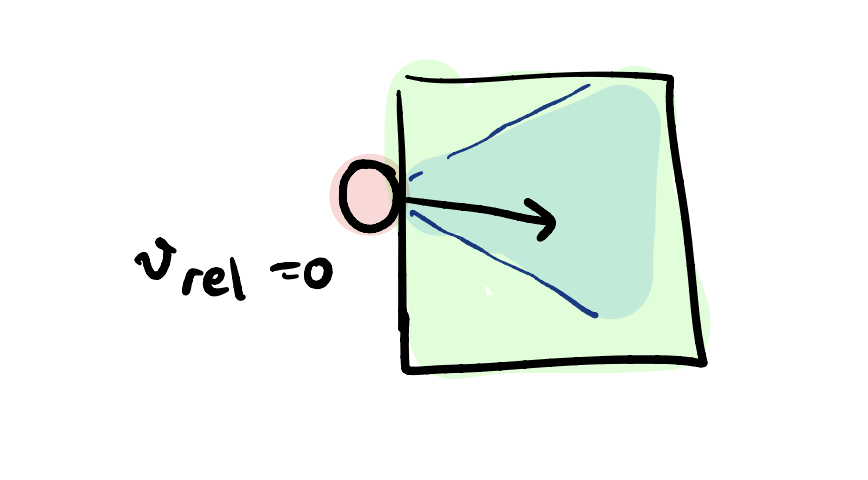
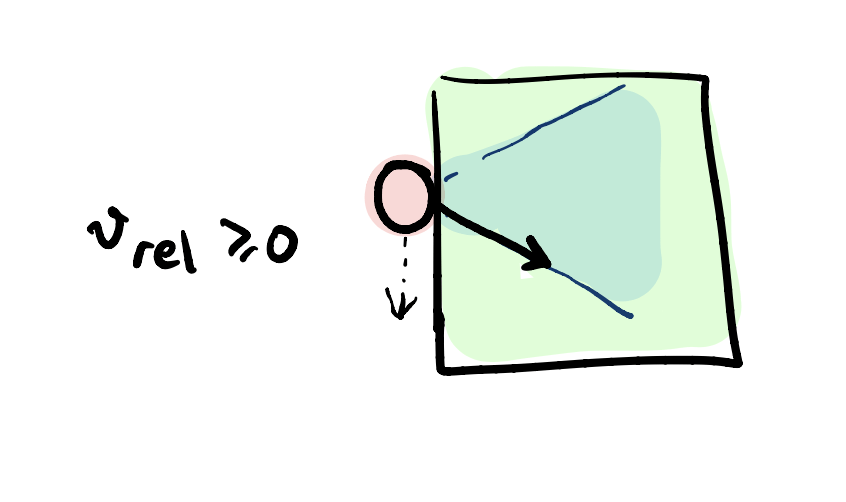
Sticking: \( | \lambda_f | \leq \mu \lambda_n \) and \( v_{\text{rel}} = 0\) 

Sliding: \( | \lambda_f | = \mu \lambda_n \) and \( |v_{\text{rel}} |  \geq 0\) 

Example: Sliding/Sticking

  • How to encode as LCP?
  • Introduce auxiliary friction force variables for each direction
  • Introduce a slack variable \( \gamma \in \R \) for \( |v_\text{rel} | \)

Sticking: \( | \lambda_f | \leq \mu \lambda_n \) and \( v_{\text{rel}} = 0\) 

Sliding: \( | \lambda_f | = \mu \lambda_n \) and \( v_{\text{rel}} \geq 0\) 

\begin{aligned} 0 \leq \gamma e + v_\text{rel} &\perp \lambda_f \geq 0 \nonumber \\ 0 \leq \mu \lambda_n - e^T \lambda_f &\perp \gamma \geq 0 \nonumber \end{aligned}
e = [1, \ldots, 1]^T
  • Enforces sticking/sliding constraints exactly (for polyhedral cones)
  • (Other LCP approximations exist, like Anitescu, etc)

J. C. Trinkle, S. Berard, and J. S. Pang, “A time-stepping scheme for quasistatic multibody systems,” 2005 (ISAPT)

T. Pang and R. Tedrake, “A Robust Time-Stepping Scheme for Quasistatic Rigid Multibody Systems,” in 2018 (IROS)

Contact in 2D

\begin{align} 0 \leq \phi(q) &\perp \lambda_n \geq 0 \quad \quad \\ 0 \leq \gamma e + v_\text{rel} &\perp \lambda_f \geq 0 \\ 0 \leq \mu \lambda_n - e^T \lambda_f &\perp \gamma \geq 0 \end{align}
e = [1, \ldots, 1]^T
  • We can describe contact/non-contact and sliding/sticking with the LCPs:

J. C. Trinkle, S. Berard, and J. S. Pang, “A time-stepping scheme for quasistatic multibody systems,” 2005 (ISAPT)

T. Pang and R. Tedrake, “A Robust Time-Stepping Scheme for Quasistatic Rigid Multibody Systems,” in 2018 (IROS)

Motion Planning in 2D

  • We formulate the motion planning problem:
  • Assume quasi-static dynamics
  • Discretize using Backward Euler
  • Decision variables:
    \((p_k, \theta_k) \in \text{SE}(2), \, \lambda_{n,k}, \lambda_{f,k} \in \R^2, \, k = 0, \ldots, N-1\)
  • Parametrize \( \theta \) by \( c_\theta, s_\theta \in \R \)
  • Bilinear expressions:
  1. LCP constraints
  2. Cross-product of arm x force
  3. SO(2)
  4. Rotation of forces

Semidefinite Relaxation

\begin{aligned} \min_{x} \quad x^\intercal Q_0 x & \\ \text{subject to} \quad x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\ \quad Ax &\geq 0 \\ \quad x &= \begin{bmatrix} 1 \\ y \end{bmatrix} \end{aligned}

Quadratic equality constraints can be formulated as:

where \(Q_i\) possibly indefinite, hence problem is nonconvex

Lift the problem:
\( x \in \R^n \rightarrow (x, X) \in \R^n \times \mathbb{S}^{n \times n}\)

\begin{aligned} \min_{x} \quad \langle Q_0, X \rangle & \\ \text{subject to} \quad \langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\ \quad AXA^\intercal &\geq 0 \\ \quad AXe_1^\intercal &\geq 0 \\ \quad e_1^\intercal X e_1 &= 1 \\ \quad X \succeq 0 \\ \end{aligned}

Equivalent when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)

Otherwise a convex relaxation

\( \longrightarrow \)

\( X := xx^\intercal \)

Result: Pushing a box

Result: Pushing a box

  • Three contact points:
  1. Finger/Box face
  2. Box left corner/table
  3. Box right corner/table
  • 1. Transitions from non-contact to contact to non-contact
  • 2. and 3. Transitions from sticking to sliding to sticking

Result: Box flip-up

Result: In-place box flip-up

  • Some obvious constraint violation
  • Seems to depend a bit on friction coeff, cost coefficients, etc.

Looks promising, but more experimentation and analysis is needed!

Conclusion:

Thoughts

  • Explicitly enumerating contact modes creates "fake" combinatorics
  • This idea relies on a linearization of the SDF around a point/in a region
  • Idea: Use GCS to plan through multiple linearization points
  • Perhaps this is closer to the "actual combinatorics" i.e. "go left/right"?

Future work

  • Test more complex systems:
  1. Multiple point fingers
  2. A one/two link finger
  • Exploit (band) sparsity

Thank you!