Towards Tight Convex Relaxations for Contact-Rich Manipulation
Bernhard Paus Graesdal, Shao Yuan Chew Chia,
Tobia Marcucci, Savva Morozov, Alexandre Amice, Pablo A. Parrilo, and Russ Tedrake
RSS 2024
Contact is everywhere
Atlas | Partners in Parkour, Boston Dynamics
Solving Rubik’s Cube with a Robot Hand, OpenAI
Meet Punyo, TRI’s Soft Robot for Whole-Body Manipulation Research, Toyota Research Institute
Let us consider a simple example
- Non-prehensile manipulation
in the plane - Behavior Cloning (BC) works well
- Scaling is hard, rely on human teleop
- Can we provide high-quality data with trajectory optimization?
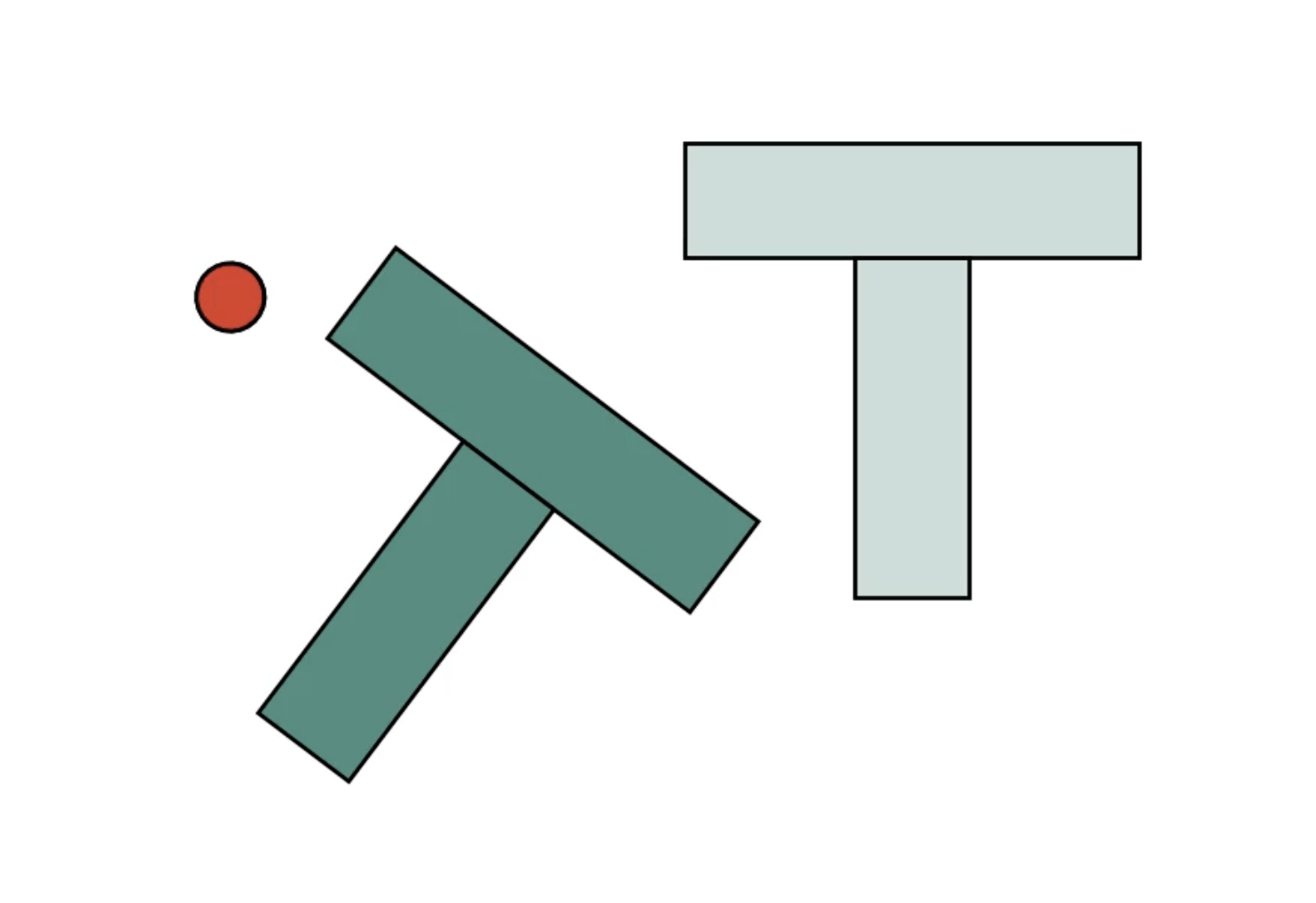
Goal: Manipulate object to target pose
“Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.”, C. Chi et al., RSS 2023
Can we solve this with trajectory optimization?
- Simple problem, but highlights difficulty for model-based planners:
-
Hybrid system:
- Where to make contact?
- What motion in each contact mode?
- Underactuated system
- Stay collision-free (between contacts)
Can we use an existing method?
- Artificially decouple discrete/continuous parts (i.e. alternating discrete/trajopt)
- Suboptimal or even low-quality trajectories
- Blend discrete and continuous, but only locally (i.e. contact-implicit methods)
- Unreliable and often fails
- Use expensive global methods that scale poorly (i.e. mixed-integer methods)
Most current methods do one of the following:
A new method based on convex optimization
1. Global
(A few percent from global optimality)
2. Reliable
(Works 100%
of the time)
3. Efficient
(Scales polynomially, not exponentially)
Step 1: Planning in a fixed mode
- Already hard:
- Rotation matrices: \( \textrm{SO}(2) \)
- Torque = arm \( \times \) force
- Don't need to solve the nonconvex problem
- Use convex semidefinite programming (SDP) relaxation
- Approximate planning (in a fixed mode) as convex program
- Use this as a building block
\( \} \)
Bilinear (nonconvex) constraints
Active face
Goal pose
Step 2: Composing the contact modes
- Graph of Convex Sets (GCS) framework
- Contact planning with GCS:
- Contact-rich planning = Solve Shortest Path Problem in GCS (convex program) + quick rounding step
“Shortest Paths in Graphs of Convex Sets,”
Marcucci et al., SIAM OPT. 2024
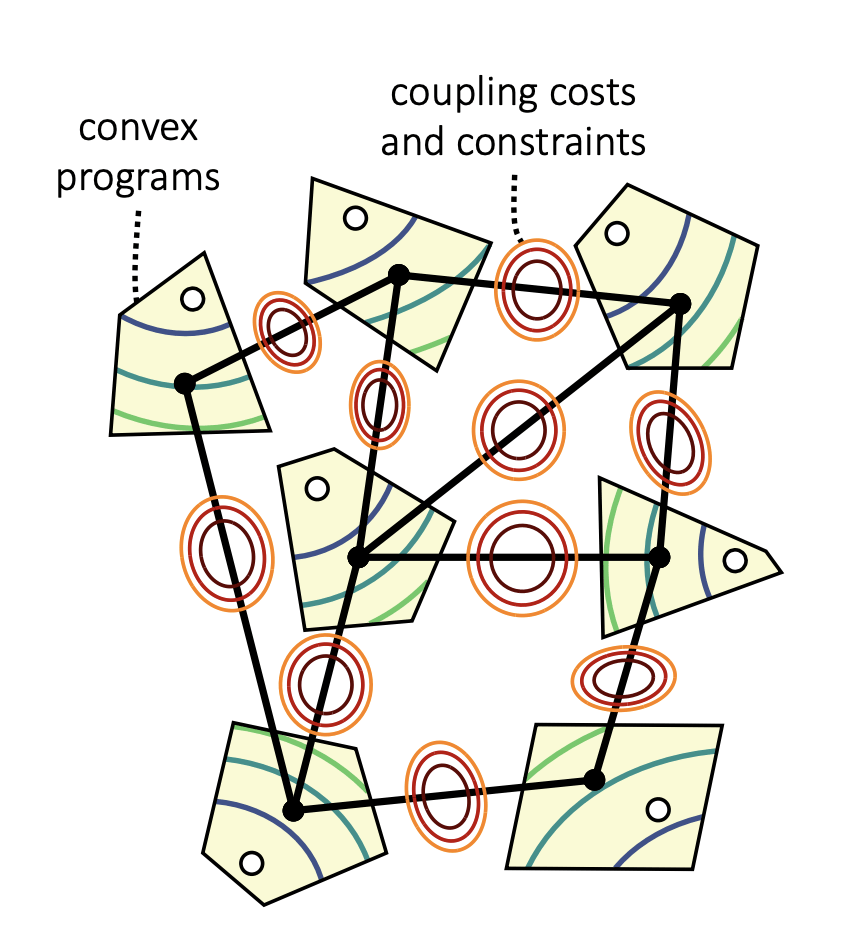
- High-level: Compose convex programs
- Computationally hard, but strong relaxation
- A vertex = Motion planning in a mode
- A path = A mode sequence
Results
-
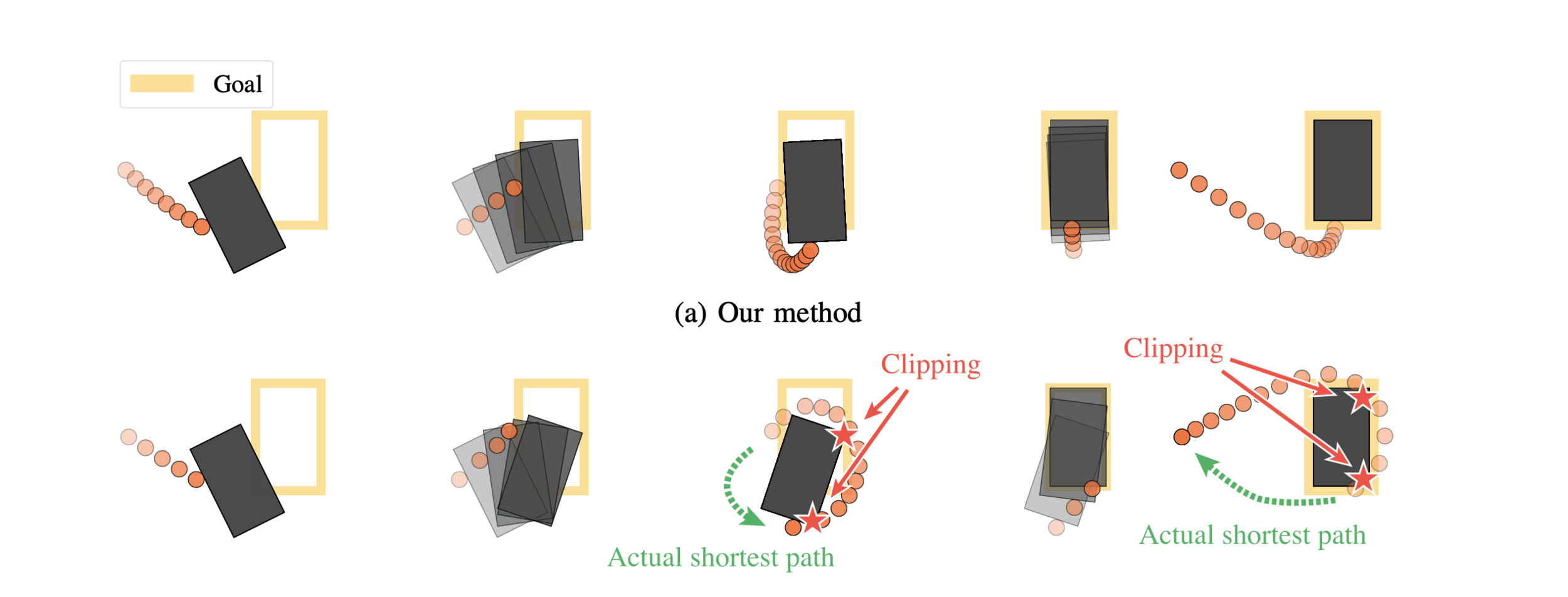
State-of-the-art comparison:
Contact-implicit trajectory optimization
-
Our method: 100% success rate
- Planning time: a few seconds to a minute
- Conservative optimality bound of 10%
- Easy case: 58% success rate
- Hard case: 12% success rate
- Struggles w/ complex mode sequences
- Global reasoning
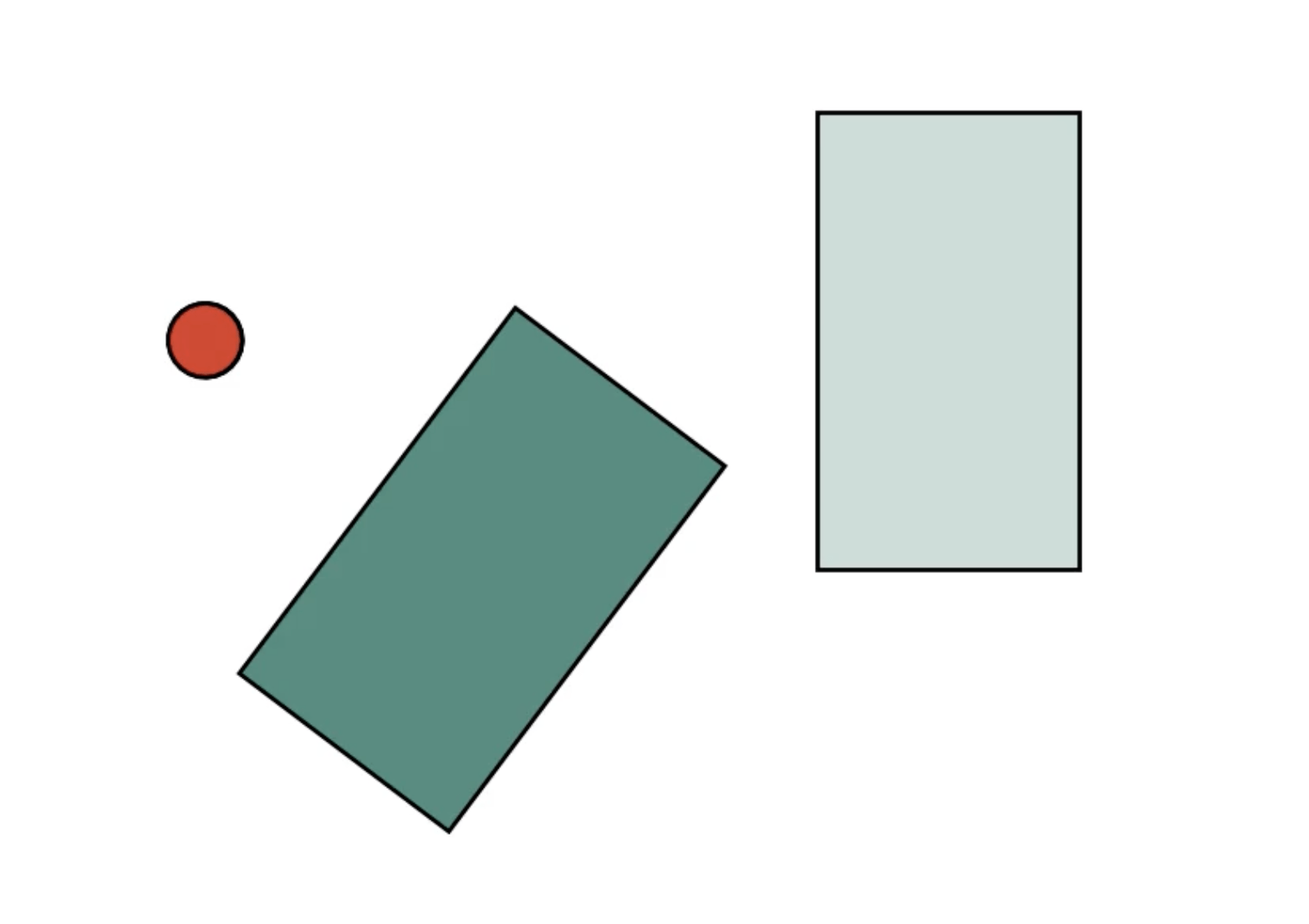
Easy (box-shape):
Hard (T-shape):
Ongoing work
- Co-training diffusion policy with 10% teleop data, 90% plans from our method
(PRELIMINARY RESULTS)
(NB: optitrack tags are not used)
Thank you!
The rest is draft slides
Use an existing motion planning method?
-
Sampling-based methods?
- Artificially decouple discrete/continuous parts
- Do not leverage rich contact dynamics
-
Local trajectory optimization?
- Blends discrete and continuous, but only locally
- Often fails
-
Global optimization?
- Expensive and scales poorly
Either this slide or the next one
Solve the problem with optimization?
- Why is this hard?
- Discrete + continuous decisions
- Where to make contact?
- What motion in each contact mode?
- Underactuated system
- Move the object by applying force
- Friction cone
- Stay collision-free between contacts
I will fix the overlap between the finger and the Tee in the video (a plotting bug)
A new method based on convex optimization
- Global (gets within a small percentage of global optimality)
- Reliable (works 100% of the time)
- Efficient (scales polynomially, rather than exponentially)
I will update with three videos that are not the same
Towards Tight Convex Relaxations for Contact-Rich Manipulation
Bernhard Paus Graesdal, Shao Yuan Chew Chia,
Tobia Marcucci, Savva Morozov, Alexandre Amice, Pablo A. Parrilo, and Russ Tedrake
RSS 2024
Contact-Rich Motion Planning is hard!
- Challenging, but important
- Examples: Locomotion and manipulation
- Hard because systems are both hybrid and underactuated
- Planner can generate high-quality training data
Solving Rubik’s Cube with a Robot Hand, OpenAI
Atlas | Partners in Parkour, Boston Dynamics
Many methods have been proposed
- Artificially decouple discrete/continuous parts (Sampling-based)
\( \rightarrow \) do not take full advantage of rich contact dynamics - Blend discrete and continuous, but only locally (Trajopt)
- Use expensive global methods (Mixed-Integer approaches)
- How to combine the best from these methods?
- Blends discrete logic and continuous dynamics into a convex program
- Leverages the rich-contact dynamics on a global level
Our method:
Challenges:
- How to handle discrete/continuous?
- How to handle nonconvex contact dynamics?
- Formulate planning as a Shortest
Path Problem in a Graph of Convex Sets (GCS) - Mixed discrete/continuous problems
- Solve to optimality with MICP
- In practive, relax and round gives good results
-
Contact planning as GCS:
- Path \(\iff \) Mode sequence
- Vertex \( \iff \) Continuous motion (in a fixed contact mode)
1. Blending discrete/continuous planning with GCS
Shortest Paths in Graphs of Convex Sets, Marcucci et al.
2. Semidefinite relaxation of contact dynamics
- We simultaneously plan poses, contact locations, and forces
- Bilinear constraints in each contact mode (nonconvex QCQP)
- We don't need to solve the nonconvex program
- Use a convex relaxation and approximate the dynamics
- Solve a convex program, get close to global optimality!
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0\\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
\begin{aligned}
\min_{x} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0\\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
X_{11} &= 1 \\
\quad
X &\succeq 0 \\
\end{aligned}
\( \iff \)
\( X := xx^\intercal \)
\(\text{(Nonconvex) QCQP}\):
\(\text{(Convex) Semidefinite Program}\):
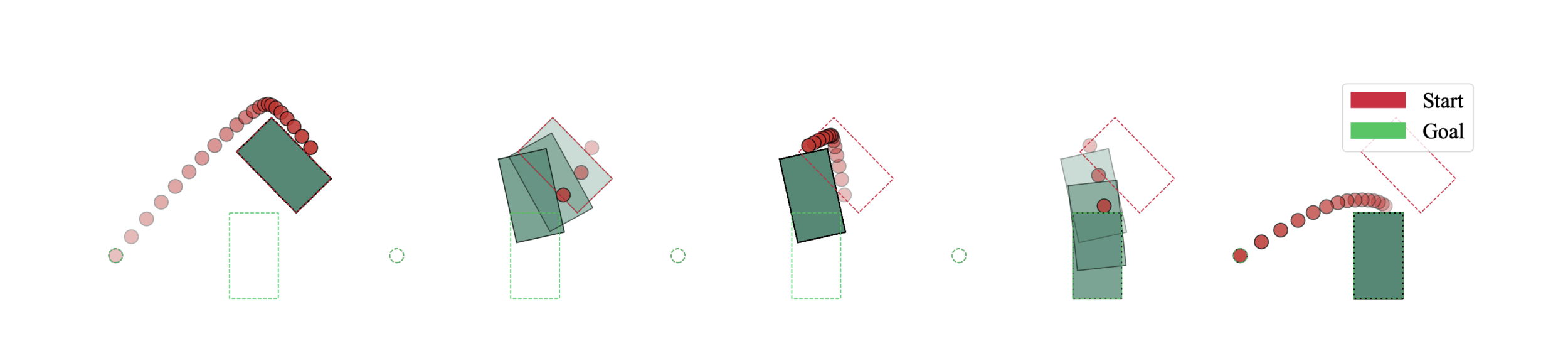
We apply our method on planar pushing
- Simple example
- State-of-the-art often fails
- Contact-implicit trajectory optimization:
- Easy case: 58% success rate
- Hard case: 12% success rate
-
Our method: 100% Success rate
(on both cases)
- Always succeeds in finding a collision-free trajectory
- Planning times: few seconds to a minute
- Upper bound of ~10% global optimality gap
- Replace left video with grid of plans
Thank you!
Comparison with direct trajectory optimization
Replace with video of the two trajectories
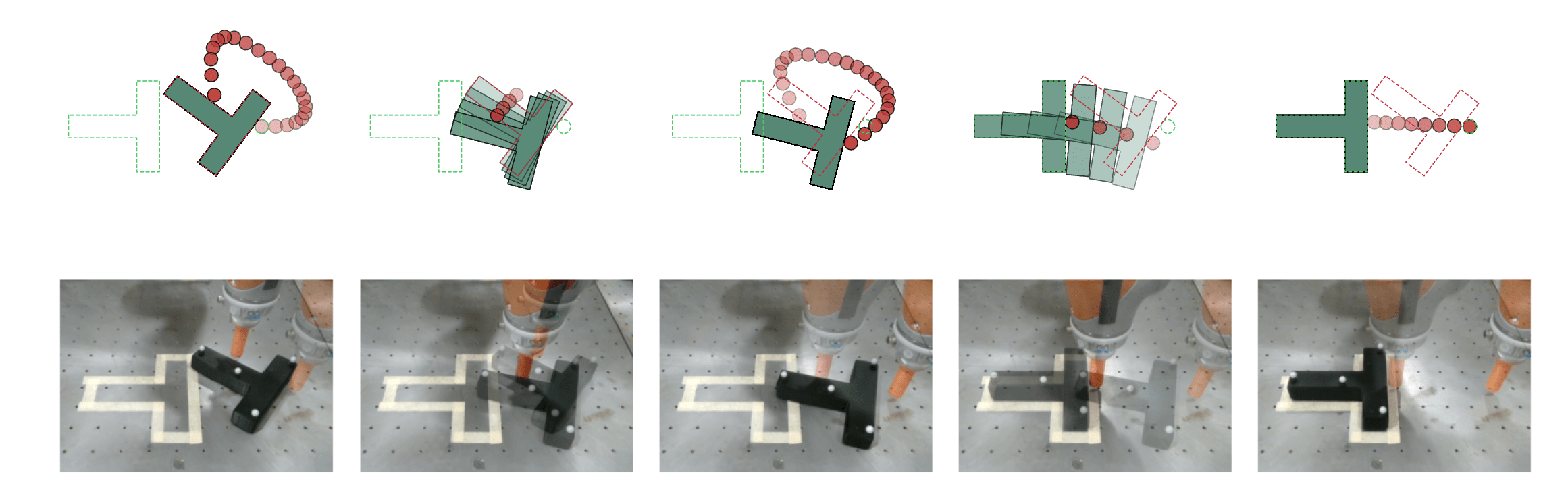
Hardware results
Talk about the plans being close to globally optimal
Motion Planning with Graphs of Convex Sets
Shortest Paths in Graphs of Convex Sets, Marcucci et al.
- Encodes discrete/continuous through a GCS
- Formulates shortest path problem as a MICP
- In practice: relax and round gives good results
Approximate nonconvex contact dynamics
- Formulate the contact problem with quadratic constraints (nonconvex)
- Relax into a convex program (SDP)
- Build a graph of contact modes
Agenda
5 minutes total
- Introduction
Thoughts
- Add MIT logo
- Dive right into contact-rich manipulation and how it is solved today
- What are the challenges with contact-rich planning?
Motivation
- Optimal planning through contact is hard
- Generally both a hybrid and underactuated system
- Existing methods often artificially decouple continuous and discrete part of the problem
Goal
A method that blends discrete logic and continuous dynamics to leverage the rich contact dynamics
Example tasks
C. Chi et al., “Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.” Mar. 09, 2023
- How do we plan for such tasks?
N. Doshi et al., “Manipulation of unknown objects via contact configuration regulation.” Jun. 01, 2022
High-Level Approach
- Formulate the problem as a Shortest Path Problem in a Graph of Convex Sets (GCS)
- Paths in the graph: Different contact sequences
- Convex sets: Model contact dynamics
- A point in a convex set \(\iff\) A trajectory within a fixed contact mode
- A feasible GCS path corresponds to a contact trajectory
\(\iff\)
Graphs of Convex Sets
-
For each \(i \in V:\)
- Compact convex set \(X_i \subset \R^d\)
- A point \(x_i \in X_i \)
- Vertex cost given by a convex function \[ \ell_v(x_i) \]
- New machinery to tighten convex relaxation
Note: The blue regions are not obstacles.
Novelty in our method
- Leverage a tight convex relaxation for the (nonconvex) bilinearities in each contact mode
- Use GCS machinery to produce a tight convex relaxation for the global planning-through-contact problem
- Obtain near-globally optimal solutions by solving a single SDP followed by a quick rounding step
- As a first step, we apply our method to planar pushing
- The approach generalizes to more complex contact-rich tasks
Planar Pushing
- Goal: Manipulate object to target pose
- One of the simplest examples of non-prehensile manipulation
- Still state-of-the-art are unable to reliably solve to global optimality
- Our method will:
- Plan a (close to) globally optimal contact-rich trajectory for manipulating the object to its target pose
- While simultaneously planning the collision-free motion between contacts
Dynamics of Planar Pushing
- Hybrid dynamical system:
- Contact and non-contact modes
- Assume quasi-static dynamics, low velocities, no work done by impacts
- Simultaneously optimize over poses and contact forces
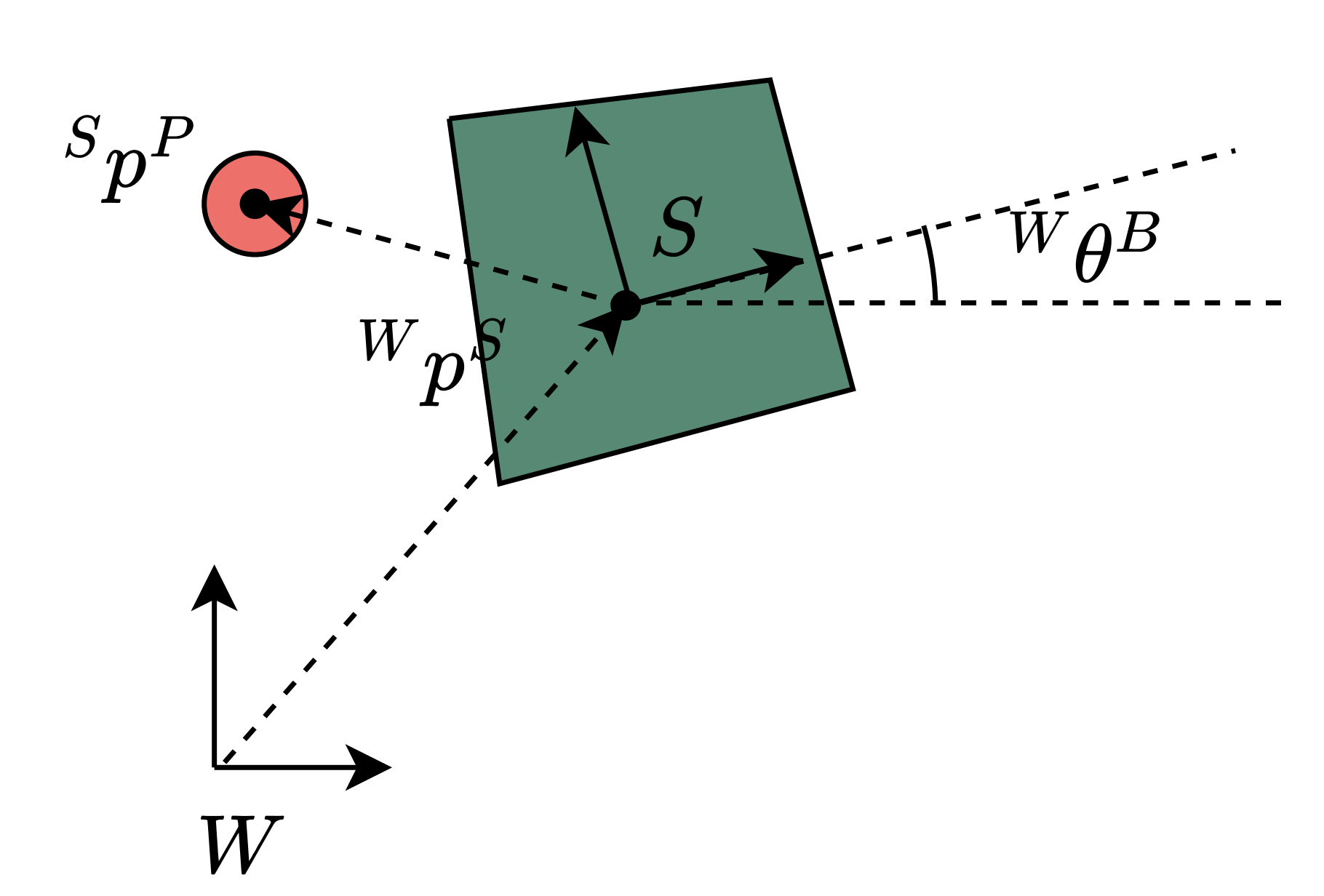
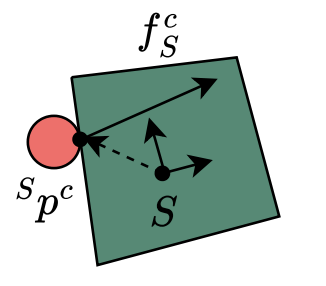
Mode class 1: Contact between the pusher and a face of the slider
- Bilinear (non-convex) dynamics due to:
- Rotation membership in \( \text{SO}(2) \)
- Cross-product between contact point and contact force (torque) in rotational dynamics
- Rotation of forces between frames in dynamics
- All can be represented with quadratic equality constraints (non-convex)
Dynamics of Planar Pushing
Mode class 2: Non-contact
- We decompose the collision-free space (similar to GCSTrajOpt) in task space
- Piecewise linear approximation of SDF in each region
- With this we can encode planning for non-contact modes as a convex problem
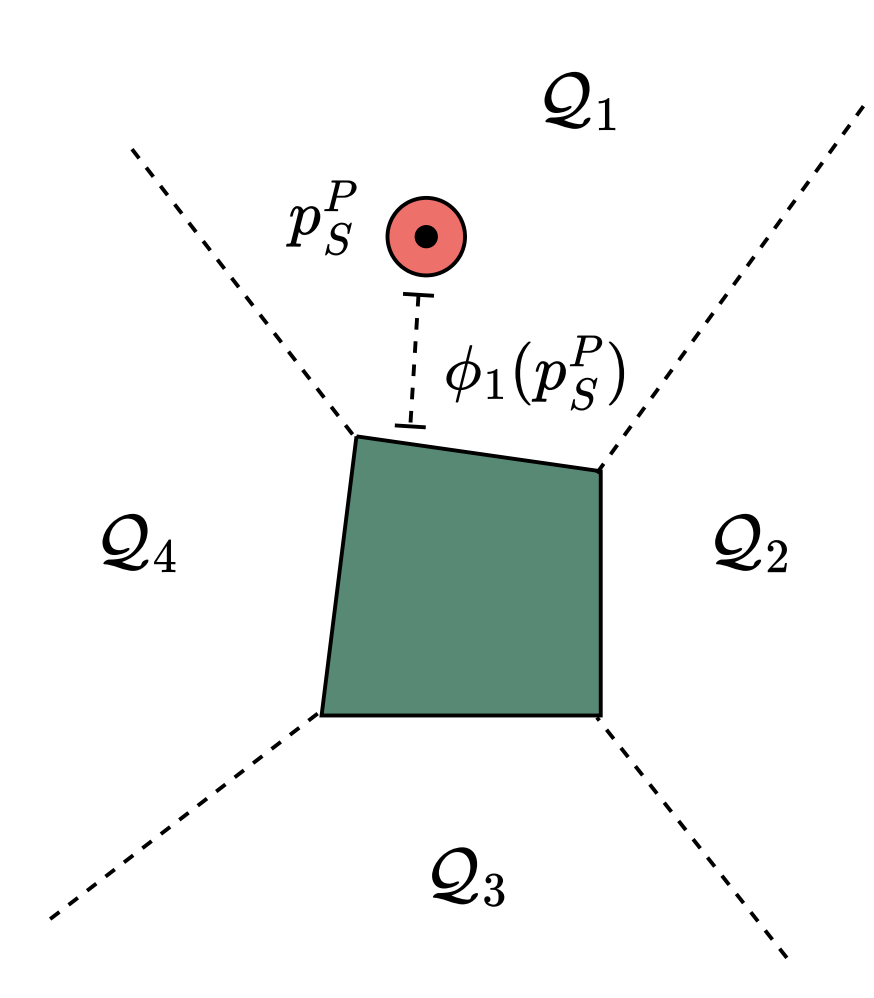
Dynamics of Planar Pushing
Semidefinite Relaxation of contact modes
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
Motion planning in a contact mode can be formulated in the form:
where \(Q_i\) possibly indefinite, hence problem is nonconvex
Lift the problem:
\( x \in \R^n \rightarrow (x, X) \in \R^n \times \mathbb{S}^{n \times n}\)
\begin{aligned}
\min_{x} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\
\quad
AXA^\intercal &\geq 0 \\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
e_1^\intercal X e_1 &= 1 \\
\quad
X \succeq 0 \\
\end{aligned}
Equivalent when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
Otherwise a convex relaxation
\( \longrightarrow \)
\( X := xx^\intercal \)
Semidefinite Relaxation of contact modes
- Tightening constraints: \( A X A^T \geq 0 \) is implied by \(Ax \geq 0\) and potentially tightens the formulation
- We have done work on finding additional tightening constraints
- Multiply quadratic constraints that simplify to new quadratic constraints (i.e. we can still use the first-order SDP relaxation!)
- Enforce the dynamics in both frames:
\( v = R u \iff R^T v = u \) is implied by \(R^T R = I\)
Motion Planning as Graph Search
- We will "Add the modes to the graph" = Add a vertex with the feasible set as the convex set and the cost as the vertex cost
- Idea: Build a graph of convex sets to represent the motion planning problem
- Planning within each fixed mode can be formulated as a convex program
Motion Planning as Graph Search
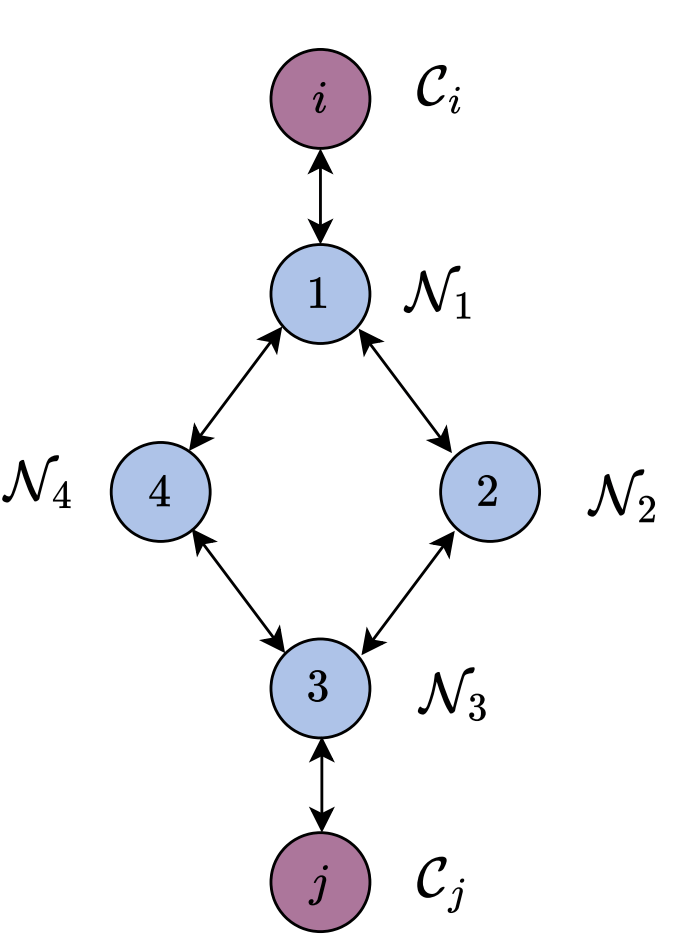
- Add a contact mode for each face of the object
- Encode collision-free motion planning between contacts: Transition through non-contact modes
- This allows transitions from any face to any face
- Allows at most one visit with a fixed horizon length to each face: can repeat the vertices in the graph to have more
- Initial and target poses as source and target (singleton) vertices in the graph
How to structure the graph and mode transitions?
\(\updownarrow\)
The motion planning algorithm
- Solve SPP in GCS problem
- Use flows as probabilities and sample N paths
- For each path: round to feasibility by solving a cheap nonlinear program from relaxed solution
- Pick the trajectory with the lowest cost
- Most expensive part is the first SDP: everything else is very cheap!
\begin{align}
\delta_\text{opt} =
\frac{C_\text{round} - C_\text{opt}}{C_\text{opt}}
\leq
\frac{C_\text{round} - C_\text{relax}}{C_\text{relax}}
= \delta_\text{relax} \nonumber
\end{align}
- We also get an upper bound on global optimality gap:
Results
Hardware experiments
(4x is due to MIQP feedback controller)
Numerical results
- Consistently within a small percentage of global optimum
- Solve times a few seconds for the box, 1.5 minutes for the Tee (box has 4 faces, tee has 8 faces)
- Expensive part is solving the big SDP. Rounding is very cheap!
- For comparison: enumerating all mode sequences and solving nonlinear program would take \( 8! \times 0.1 s \approx 67\) minutes (assuming the nonlinear program always gave a good solution)
(Reported values are mean values, with median in parenthesis)
Numerical results
- We have not yet compared to MINLP which we will do for the paper rebuttal
(Reported values are mean values, with median in parenthesis)
Preprint available on Arxiv: https://arxiv.org/abs/2402.10312
Future directions...
Policy
Training
Data
Trajectory Generation
GCS \( \rightarrow \) BC w/ Diffusion Policy
Example: Push-T Task (with Kuka)
- Use GCS for data generation
\(\rightarrow\) Train BC policy directly on data
Adam Wei
Planning through contact for general manipulation
- Addresses scalability by avoiding explicit enumeration of contact modes
- Plan: Decompose the space into convex regions and use GCS to plan through these