Towards Tight Convex Relaxations for Contact-Rich Manipulation
Amazon Presentation
February 22nd 2024
Bernhard Paus Graesdal

Preprint available on Arxiv: https://arxiv.org/abs/2402.10312
Motivation
- Optimal planning through contact is hard:
- Problem is combinatorial and continuous
- Existing methods are local and often unreliable
- ...or use expensive global optimization
- Want to leverage rich contact dynamics through global planning

Goal
- A method that is able to naturally blend discrete logic and continuous dynamics to do global contact-rich planning
- (We will be using GCS)
High-Level Approach
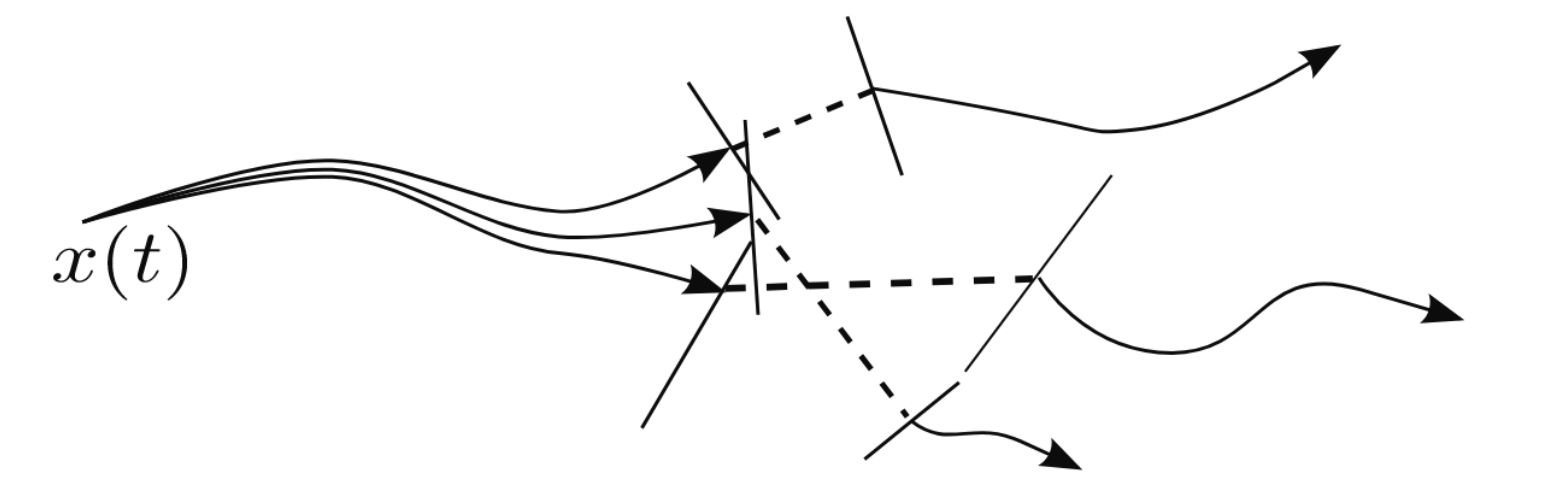
- Formulate the problem as a Shortest Path Problem (SPP) in a Graph of Convex Sets (GCS)
- Paths in the graph: Different contact sequences
- Convex sets: Model contact dynamics
- A feasible GCS path corresponds to a contact trajectory!

High-Level Approach
- However...
- Quasi-static contact dynamics are bilinear, hence nonconvex
- Approximate with convex relaxations
- In particular: Use a tight semidefinite relaxation for each contact mode
- Can retrieve a feasible solution with a quick rounding step
Problem Formulation
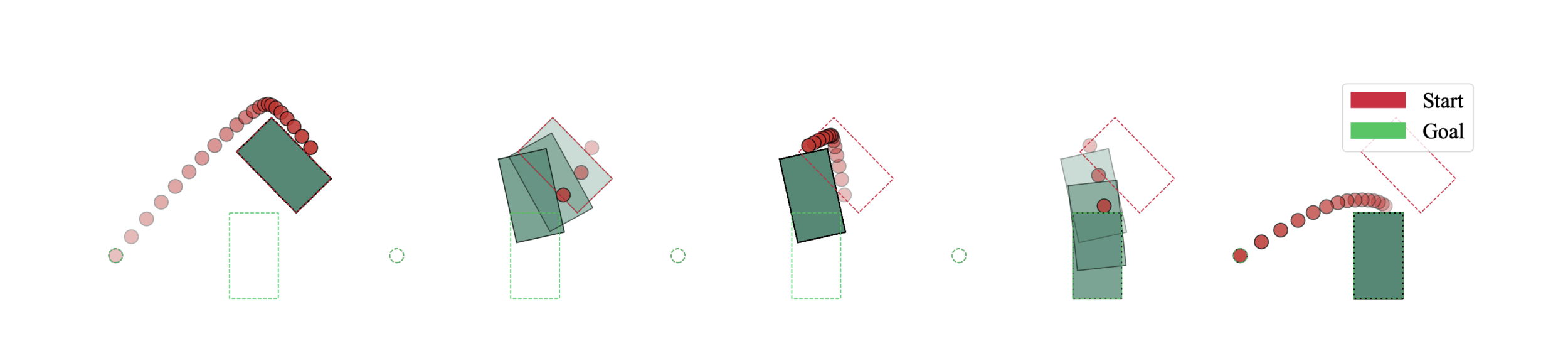
- As a first step, we apply our method to planar pushing

- Goal: Manipulate object to target pose
- Simple example of non-prehensile manipulation
- State-of-the-art unable to reliably solve to global optimality
- Our method: Plan contact-rich trajectory, collision-free between contacts, close to global optimality
Dynamics of Planar Pushing
- Hybrid dynamical system:
- Contact modes and non-contact modes
- Assume quasi-static dynamics, low velocities and no work done by impacts
- Simultaneously optimize over poses and contact forces
- Assume polygonal geometry

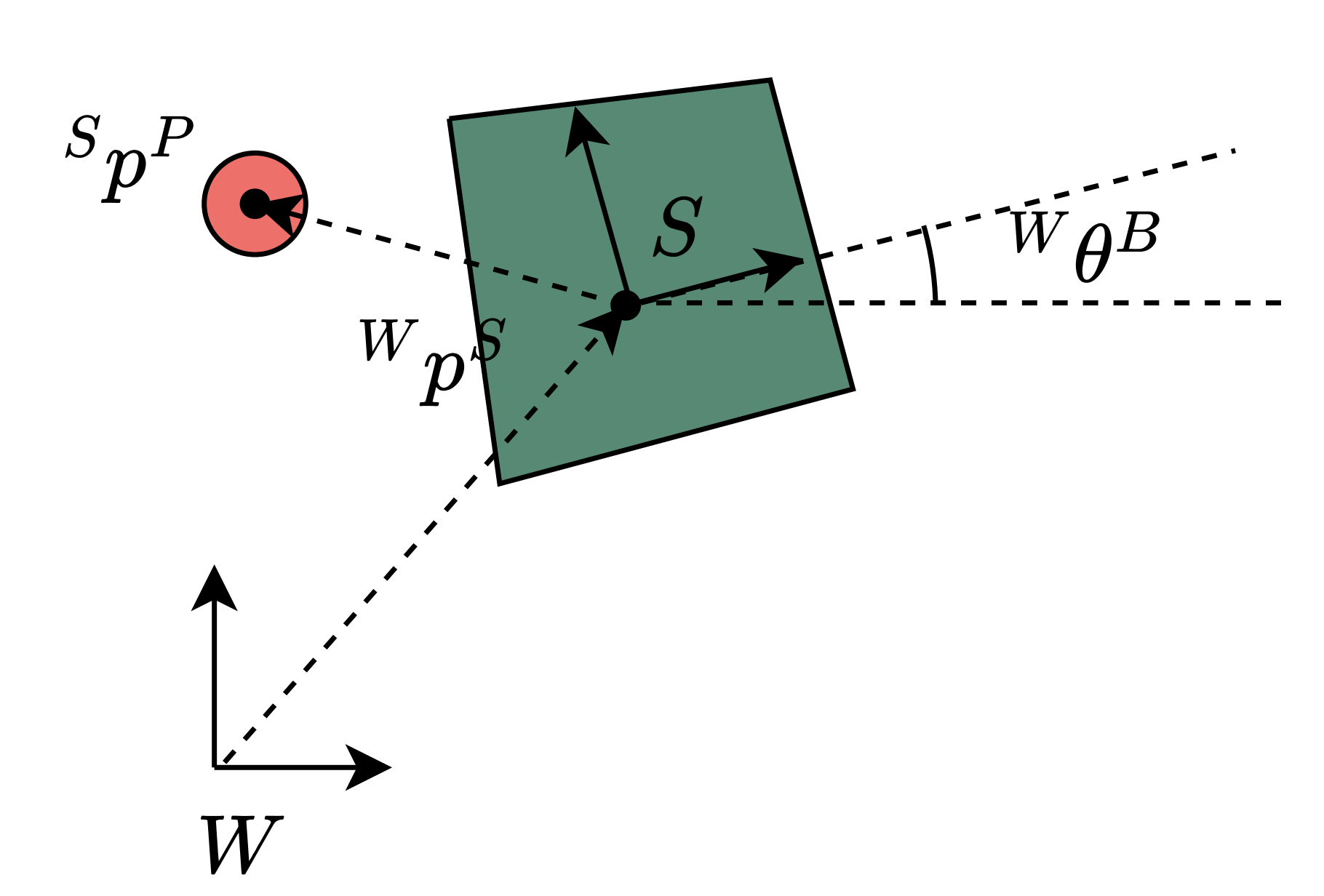
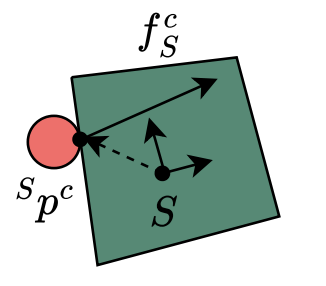
The Slider-Pusher System
Contact modes:
- Bilinear (non-convex) dynamics due to:
- \( \text{SO}(2) \) is nonconvex
- Cross-product between contact point and contact force (torque)
- Rotation of forces between frames
- Quadratic equality constraints
- Relax using Semidefinite Programming

Details: Semidefinite Relaxation
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
Motion planning in a contact mode can be formulated in the form:
where \(Q_i\) possibly indefinite, hence problem is nonconvex
Lift the problem:
\( x \in \R^n \rightarrow (x, X) \in \R^n \times \mathbb{S}^{n \times n}\)
\begin{aligned}
\min_{x} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\
\quad
AXA^\intercal &\geq 0 \\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
e_1^\intercal X e_1 &= 1 \\
\quad
X \succeq 0 \\
\end{aligned}
Equivalent when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
Otherwise a convex relaxation
\( \longrightarrow \)
\( X := xx^\intercal \)
The Slider-Pusher System
Non-contact modes:
- We decompose the collision-free space (similar to GCSTrajOpt) in task space
- Piecewise linear approximation of SDF
- \(\implies\) Can encode planning for non-contact as a convex problem

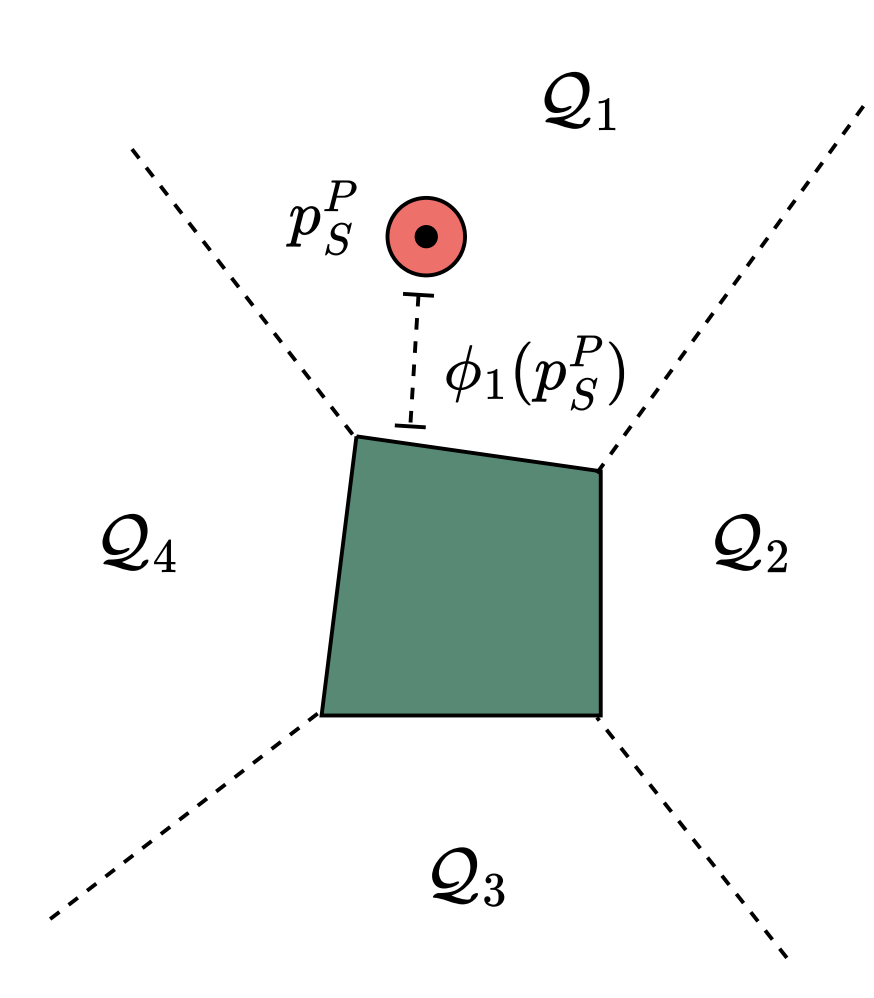
Motion Planning as Graph Search
- One vertex per contact mode
- Collision-free motion between contact: Add non-contact modes as vertices between all the contact modes
- Initial and target positions as source and target in the graph

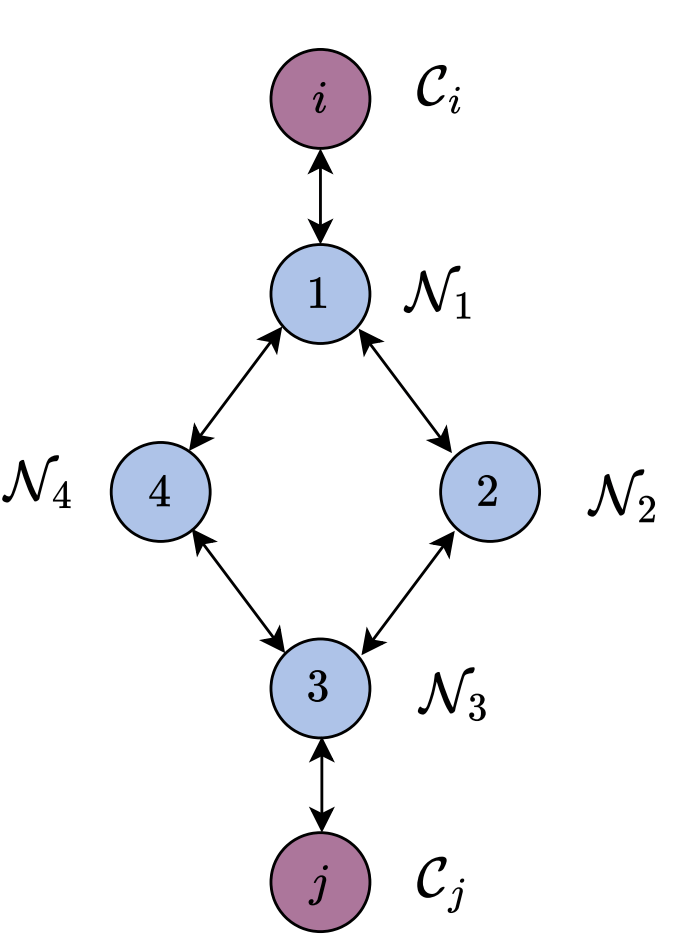


The motion planning algorithm
- Solve SPP in GCS problem
- Retrieve N paths
- Round paths using cheap nonlinear rounding step to get dynamically feasible trajectory
- Pick the trajectory with the lowest cost
\begin{align}
\delta_\text{opt} =
\frac{C_\text{round} - C_\text{opt}}{C_\text{opt}}
\leq
\frac{C_\text{round} - C_\text{relax}}{C_\text{relax}}
= \delta_\text{relax} \nonumber
\end{align}
- We also get an upper bound on global optimality gap:

Results
Hardware experiments
(4x is due to MIQP feedback controller)
Numerical results

- Consistently within a small percentage of global optimum
- Solve times a few seconds for the box, 1.5 minutes for the Tee (box has 4 faces, tee has 8 faces)
- We scale ~quadratically with number of faces
(much better than exhaustive mode enumeration)
(Reported values are mean values, with std. shown in parenthesis)
Future directions...
- While our method scales better than other global methods, it explicitly enumerates contact modes when building the graph
- This gets very expensive for multiple bodies!
- Next step: leverage the same machinery of convex relaxations to avoid enumeration
- Convex relaxations for complimentarity constraints
Preliminary results
- No enumeration of contact modes
- Relies only on LCP constraints and semidefinite relaxations
- Uses a linear approximation of SDF
- Idea: Use GCS to plan through these linearizations