Graphs and Trees
Part 3 and 4 of
Practical Data Structures and
Algorithms for Interviews
slides.com/bgando/intro-graph-trees

Common Interview DS
| DS | Common Uses | FEM Course |
|---|---|---|
| Arrays & Strings | ordered data, words | Part 2 |
| Hash Tables | optimization | Part 2 |
| Linked Lists | data insert/delete | Part 2 |
| Stacks/Queues | creative aux DS | Part 2 |
| Graphs | complex relationships | Part 3 (this one) |
| Trees | hierarchical data | Part 4 (this one) |
What will we cover today?
Trees
Graphs
Binary Search Trees



How to be effective
Rule #1 don't aim to memorize, this will not help!
Rule #2 find themes, but don't jump to conclusions
Rule #3 practice with a timer, speed matters
Rule #3.5 actually practice, reading doesn't count
Rule #4 communicate and be nice


Linear Data Structures




Array
Linked List
Stack
Queue
Linear Data Structures

Array
Insert at end:
Insert at beginning:
Insert (generally):
Remove from end:
Remove from beginning:
Remove (generally):
Find value:
Access value:
Linear Data Structures

Array
Insert at end: O(1)
Insert at beginning: O(n)
Insert (generally): O(n)
Remove from end: O(1)
Remove from beginning: O(n)
Remove (generally): O(n)
Find value: O(n)
Access value: O(1)
Linear Data Structures
Linked List

Insert at end:
Insert at beginning:
Insert (generally):
Remove from end:
Remove from beginning:
Remove (generally):
Find value:
Access value:
Linear Data Structures
Linked List

Insert at end: O(1)
Insert at beginning: O(1)
Insert (generally): O(1)
Remove from end: O(1)
Remove from beginning: O(1)
Remove (generally): O(1)
Find value: O(n)
Access value: O(n)
Linear Data Structures
Stack

Insert at end:
Insert at beginning:
Insert (generally):
Remove from end:
Remove from beginning:
Remove (generally):
Find value:
Access value:
Linear Data Structures
Stack

Insert at end: O(1)
Insert at beginning: N/A
Insert (generally): O(1)
Remove from end: O(1)
Remove from beginning: N/A
Remove (generally): O(1)
Find value: O(n)
Access value: O(n)
Linear Data Structures
Queue

Insert at end:
Insert at beginning:
Insert (generally):
Remove from end:
Remove from beginning:
Remove (generally):
Find value:
Access value:
Linear Data Structures
Queue

Insert at end: N/A
Insert at beginning: O(n) or O(1)
Insert (generally): O(1) with linked list
Remove from end: O(1)
Remove from beginning: N/A
Remove (generally): O(1)
Find value: O(n)
Access value: O(n)
Linear Data Structures




Array
Linked List
Stack
Queue
| LINEAR DATA STRUCTURE | NON-LINEAR DATA STRUCTURE | |
|---|---|---|
| Overview | arranged in an orderly manner where the elements are attached adjacently | arranged with multiple relationships and properties to describe them |
| Traversing | can be accessed in one time (single run) | traversing is best handled recursively |
| Ease of implementation | simpler | complex |
| Levels involved | single level | multiple level |
| Examples | array, queue, stack, linked list, etc. | tree and graph |
Anyone have a morning routine?

Expectation

Expectation


Reality
Create a data structure to model a chat-bot that helps you decide what to eat for breakfast by asking yes or no questions.

{
question: 'Do you feel like cooking?',
yes: <question>,
no: <question>
}
1. create a data structure
2. model a chat-bot that
3. helps you decide what to eat for breakfast
4. by asking yes or no questions.
?
Yes
No
Recommendation
{
question: 'Do you feel like cooking?',
yes: <question>,
no: <question>
}
{
question: 'Do you have milk?',
yes: <question>,
no: <question>
}
1. create a data structure
2. model a chat-bot that
3. helps you decide what to eat for breakfast
4. by asking yes or no questions.

Yes
No
Recommendation

{
question: 'Do you feel like cooking?',
yes: <question>,
no: <question>
}
{
question: 'Do you have milk?',
yes: <question>,
no: <question>
}
{
question: 'Do you have toast?',
yes: <question>,
no: <question>,
recommendation: 'You should make toast for breakfast!'
}1. create a data structure
2. model a chat-bot that
3. helps you decide what to eat for breakfast
4. by asking yes or no questions.

Yes
No
Recommendation

const chatBot = {
question: 'Do you feel like cooking?',
yes: {
question: 'Do you have milk?',
yes: <question>,
no: <question>
},
no: {
question: 'Do you have toast?',
yes: <question>,
no: <question>
}
}
1. create a data structure
2. model a chat-bot that
3. helps you decide what to eat for breakfast
4. by asking yes or no questions.

?
Yes
No
Recommendation
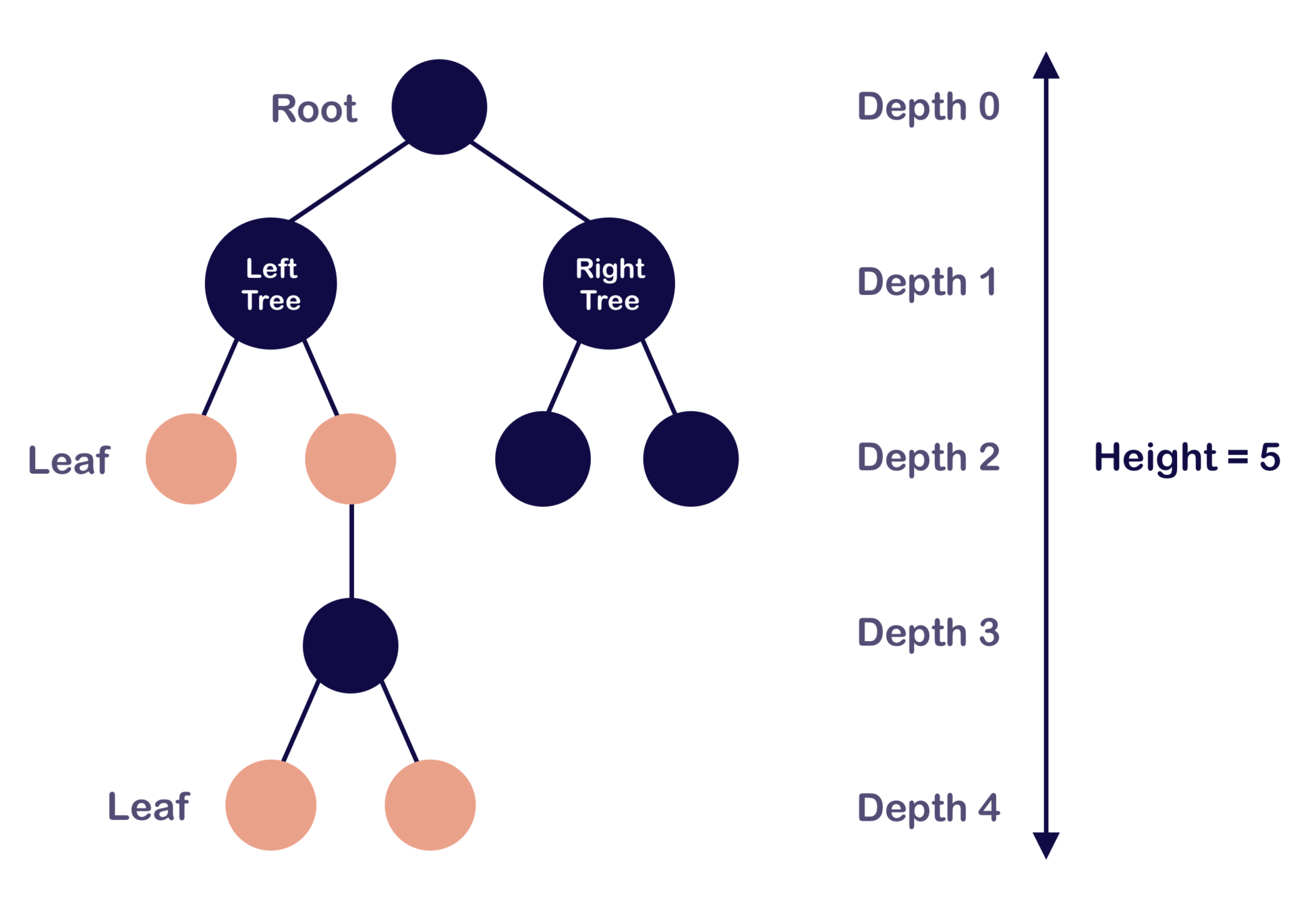
Trees - Terminology

eat toast!


eat toast!

The DOM is a tree.
Parsers use trees to model the structure of code
Autocomplete features use a special kind of tree called a trie.
Trees - Terminology
Non-Linear to Linear?
const chatBot = {
question: 'Do you feel like cooking?',
yes: {
question: 'Do you have milk?',
yes: <question>,
no: <question>
},
no: {
question: 'Do you have toast?',
yes: <question>,
no: <question>
}
}


const mother = { name: 'Ashleigh' };
const son = { name: 'Sammy' };
const daughter = { name: 'Alex' };
Family Trees
const mother = { name: 'Ashleigh' };
const son = { name: 'Sammy' };
const daughter = { name: 'Alex' };
const mother = {
name: 'Ashleigh',
children: [son, daughter]
};Family Trees
/** Class representing a Tree. */
class Tree {
constructor(value) {
}
/*
* Adds a new value as a child of the tree
* @param {*} value the value to add
*/
insertChild(value) {
}
/*
* Removes a value from the tree
* @param {*} value the value to remove
*/
removeChild(value) {
}
}
const myTree = new BinaryTree();
console.log(myTree)

Insert: O(1)
Remove: ??
Traverse: ??
class Tree {
constructor(value) {
this.value = value;
this.children = [];
}
insertChild(value) {
const newTree = new Tree(value);
this.children.push(newTree);
return newTree;
}
removeChild(value) {
// ??
}
}
Count all possible
chat-bot recommendations.



const chatBot = {
question: 'Do you feel like cooking?',
yes: {
question: 'Do you have milk?',
yes: <question>,
no: <question>
},
no: {
question: 'Do you have toast?',
yes: <question>,
no: <question>
}
}
Q1
Q2
Q3


const chatBot = {
question: 'Do you feel like cooking?',
yes: {
question: 'Do you have milk?',
yes: <question>,
no: <question>
},
no: {
question: 'Do you have toast?',
yes: <question>,
no: <question>
}
}



Q1
Q2
Q3


Leaf nodes are the recommendations!
Binary Trees - Traversals
Preorder: Node, then children (starting left)





Q1
Q2
Q3


Q1
Q2
Q3


function traverse(tree) {
...
}const mother = { name: 'Ashleigh' };
const son = { name: 'Sammy' };
const daughter = { name: 'Alex' };
const mother = {
name: 'Ashleigh',
children: [son, daughter]
};function traverse(tree) {
...
}const family = {
name: 'Ashleigh',
children: [{
name: 'Sammy',
children: [{
name: 'Bowser',
children: [{ name: 'P' }],
}],
},
{ name: 'Alex' }]
};
/** Class representing a Binary Tree. */
class BinaryTree {
constructor(value) {
}
/*
* Explores all the nodes in the tree
*/
traverse() {
}
/*
* Returns true if value is found
*/
contains(value) {
}
}
const myTree = new BinaryTree();
console.log(myTree) Fixed Operations
contains(val), size(tree), traverse(tree)
Dynamic Operations
insert(x, y), remove(node),
reOrder(x, y)
function traverse(tree) {
console.log(tree.name);
tree.children.forEach((child)=> {
traverse(child);
});
}// if node is null, return 0.
// elseIf yes and no child nodes are null, return 1
// else recursively calculate
// Leaf count of left subtree +
// Leaf count of right subtree
function countReccos(tree) {
console.log(tree.name);
tree.children.forEach((child)=> {
traverse(child);
});
}
Insert:
Remove:
Traverse:
countReccos:
Preorder: Node, then children (starting left)
Inorder: Left child recursively, Node, Right child
Postorder: Children recursively, then Node
+







Q1
Q2
Q3




Q1
Q2
Q3


Q3

Q2
Q1


Q3
Q2

Q1
Binary Trees - Traversals
// left, root, right
function inOrder(node, func = console.log) {
if (node.left) {
node.left.inOrder(func);
}
func(node);
if (node.right) {
node.right.inOrder(func);
}
}
// root, left, right
function preOrder(node, func = console.log) {
func(node);
if (node.left) {
node.left.preOrder(func);
}
if (node.right) {
node.right.preOrder(func);
}
}// left, right, root
function postOrder(node, func = console.log) {
if (node.left) {
node.left.postOrder(func);
}
if (node.right) {
node.right.postOrder(func);
}
func(node);
}

No
Do you want toast?
No!
Am I being helpful?
...?
Let's create a data structure to model a better breakfast recommendation engine!

Draw it!












Consider the breakfast foods of myself and my friends. How could you represent this as a graph?
A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.

















































A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.

























A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.


























A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.



























A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.




























A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.




























A − B,
A − C,
A − E,
B − D,
C − D,
C . − E.






Graph

Graph Implementation

Let's create a data structure to model a better breakfast recommendation engine!

Aren't you so excited?





First Step
What data needs to be stored?






What data needs to be stored?






1
4
3
2
5
First Step
Adjacency Matrix
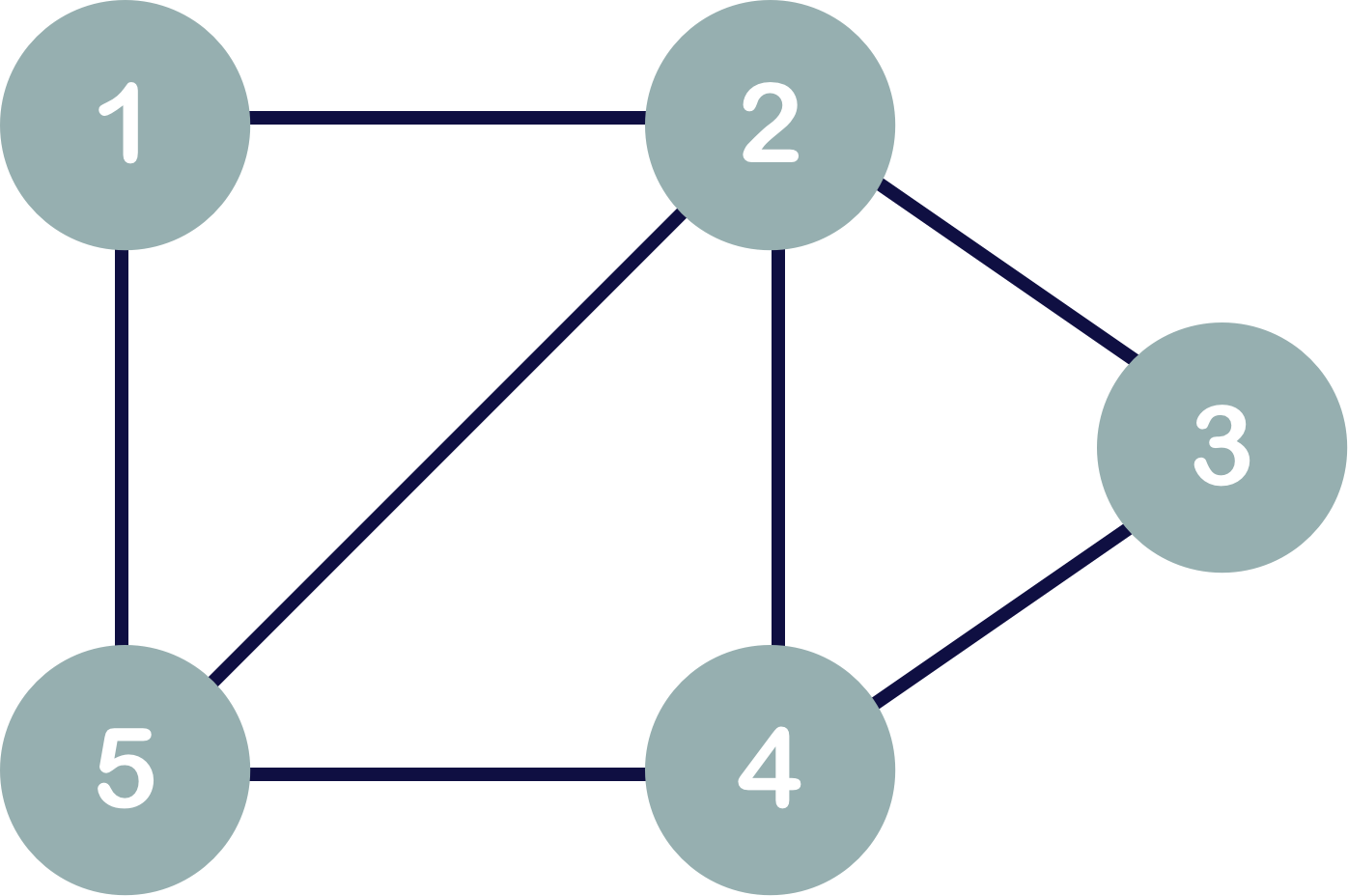















Adjacency Matrix


Adjacency Matrix

Vertices
Vertices

Edges
Adjacency Matrix

Vertices
Vertices

Edges
[[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]];
addEdge(v1,v2);Adjacency Matrix
Vertices
Vertices

Edges
[[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]];function addEdge(v1, v2) {
adjMatrix[v1][v2] = 1;
adjMatrix[v2][v1] = 1;
}
addEdge(v1,v2);Adjacency Matrix
Vertices
Vertices

Edges
[[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]];function addEdge(v1, v2) {
adjMatrix[v1][v2] = 1;
adjMatrix[v2][v1] = 1;
}
addEdge(v1,v2);
removeEdge(v1,v2)Adjacency Matrix
Vertices
Vertices

Edges
[[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]];function addEdge(v1, v2) {
adjMatrix[v1][v2] = 1;
adjMatrix[v2][v1] = 1;
}
addEdge(v1,v2);
function removeEdge(v1, v2) {
adjMatrix[v1][v2] = 0;
adjMatrix[v2][v1] = 0;
}
removeEdge(v1,v2)Adjacency Matrix
Vertices
Vertices

Edges
[[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]];function addEdge(v1, v2) {
adjMatrix[v1][v2] = 1;
adjMatrix[v2][v1] = 1;
}
addEdge(v1,v2);
function removeEdge(v1, v2) {
adjMatrix[v1][v2] = 0;
adjMatrix[v2][v1] = 0;
}
removeEdge(v1,v2)Time Complexity?
Vertices
Vertices

Edges
[[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]];
Vertices
Edges
Adjacency List


addEdge(v1,v2);
const adjList = {
1:[2,5],
2:[1,5,3,4],
3:[2,4],
4:[2,5,3],
5:[4,1,2]
}Vertices
Edges
Adjacency List

function addEdge(v1, v2) {
adjList[v1].push(v2);
adjList[v2].push(v1);
}
addEdge(v1,v2);
const adjList = {
1:[2,5],
2:[1,5,3,4],
3:[2,4],
4:[2,5,3],
5:[4,1,2]
}Vertices
Adjacency List
Edges

function addEdge(v1, v2) {
adjList[v1].push(v2);
adjList[v2].push(v1);
}
addEdge(v1,v2);
removeEdge(v1,v2)const adjList = {
1:[2,5],
2:[1,5,3,4],
3:[2,4],
4:[2,5,3],
5:[4,1,2]
}Vertices
Adjacency List
Edges

function addEdge(v1, v2) {
adjList[v1].push(v2);
adjList[v2].push(v1);
}
addEdge(v1,v2);
function removeEdge(v1, v2) {
const v2Index = adjList[v1].indexOf(v2);
const v1Index = adjList[v2].indexOf(v1);
adjList[v1].splice(v2Index, 1);
adjList[v2].splice(v1Index, 1);
}
removeEdge(v1,v2)const adjList = {
1:[2,5],
2:[1,5,3,4],
3:[2,4],
4:[2,5,3],
5:[4,1,2]
}Vertices
Adjacency List
Edges

function addEdge(v1, v2) {
adjList[v1].push(v2);
adjList[v2].push(v1);
}
addEdge(v1,v2);
function removeEdge(v1, v2) {
const v2Index = adjList[v1].indexOf(v2);
const v1Index = adjList[v2].indexOf(v1);
adjList[v1].splice(v2Index, 1);
adjList[v2].splice(v1Index, 1);
}
removeEdge(v1,v2)const adjList = {
1:[2,5],
2:[1,5,3,4],
3:[2,4],
4:[2,5,3],
5:[4,1,2]
}Vertices
Time Complexity?
Edges
Adjacency List
function addEdge(v1, v2) {
adjList[v1].push(v2);
adjList[v2].push(v1);
}
addEdge(v1,v2);
function removeEdge(v1, v2) {
const v2Index = adjList[v1].indexOf(v2);
const v1Index = adjList[v2].indexOf(v1);
adjList[v1].splice(v2Index, 1);
adjList[v2].splice(v1Index, 1);
}
removeEdge(v1,v2)function addEdge(v1, v2) {
adjMatrix[v1][v2] = 1;
adjMatrix[v2][v1] = 1;
}
addEdge(v1,v2);
function removeEdge(v1, v2) {
adjMatrix[v1][v2] = 0;
adjMatrix[v2][v1] = 0;
}
removeEdge(v1,v2)Adjacency Matrix
/** Class representing a Graph. */
class Graph {
constructor(value) {
}
* Adds a new value
* @param {*} value the value to add
*/
addNode(value) {
}
* Adds an edge between nodeA and nodeB
* @param {*} nodes to connect
*/
addEdge(nodeA, nodeB) {
}
* Removes a node
* @param {*} node to remove
*/
removeNode(node) {
}
}
const myGraph = new Graph();
console.log(myGraph)

Let's make some recommendations!
















































A
C
6
3
4
B
2
8
const adjList = {
A:[2,3,4],
2:[A],
3:[A,B],
4:[A,B,C],
B:[4,3,6]
...
}
DFS vs BFS
4
7










DFS vs BFS
DFS vs BFS
4
7


Depth First!
DFS
4
7

DFS

1
DFS

1
2
DFS

1
2
3
DFS

1
2
3
4
DFS

1
2
5
3
4
DFS

1
2
5
3
6
4
DFS

1
2
5
3
6
4
7
DFS

1
2
5
3
6
8
4
7
DFS

1
2
5
9
3
6
8
4
7
DFS

1
2
5
9
3
6
8
4
7
10
Graph Exploration
const adjList = {
1:[2,3,4],
2:[1],
3:[1,5],
4:[1,5,7],
5:[4,3,6]
...
}
1. Add unvisited vertex to stack
2. Mark vertex as visited
3. If vertex has unvisited children
- repeat 1-2 with child
4. If vertex has no unvisited children
- pop from stack
5. repeat until stack is empty
DFS
1. Add unvisited vertex to stack
2. Mark vertex as visited
3. If vertex has unvisited children
- repeat 1-2 with child
4. If vertex has no unvisited children
- pop from stack
5. repeat until stack is empty

1
2
5
9
3
6
8
4
7
10
DFS
{ 1: [2, 3, 4] }const stack = [1 ]
visited = {
}1. Add unvisited vertex to stack

DFS
{ 1: [2, 3, 4] }const stack = [1 ]
visited = {
1: true,
}2. Mark vertex as visited

DFS
{ 1: [2, 3, 4] }{ 2: [5] }const stack = [1, 2 ]
visited = {
1: true,
2: true,
}3. If vertex has unvisited children
- repeat 1-2 with child

DFS
{ 1: [2, 3, 4] }{ 2: [5] }{ 5: [9] }const stack = [1, 2, 5 ]
visited = {
1: true,
2: true,
5: true,
}
DFS
{ 1: [2, 3, 4] }{ 2: [5] }{ 5: [9] }{ 9: [] }const stack = [1, 2, 5, 9]
visited = {
1: true,
2: true,
5: true,
9: true
}
DFS
{ 1: [2, 3, 4] }{ 2: [5] }{ 5: [9] }{ 9: [] }const stack = [1, 2, 5, 9]
visited = {
1: true,
2: true,
5: true,
9: true
}


DFS

{ 1: [2, 3, 4] }{ 2: [5] }{ 5: [9] }const stack = [1, 2, 5, ]
visited = {
1: true,
2: true,
5: true,
9: true
}DFS

{ 1: [2, 3, 4] }{ 2: [5] }{ 5: [9] }const stack = [1, 2, 5, ]
visited = {
1: true,
2: true,
5: true,
9: true
}

DFS

{ 1: [2, 3, 4] }{ 2: [5] }const stack = [1, 2, ]
visited = {
1: true,
2: true,
5: true,
9: true
}

DFS

{ 1: [2, 3, 4] }const stack = [1, ]
visited = {
1: true,
2: true,
5: true,
9: true
}5. repeat until stack is empty
DFS

{ 1: [2, 3, 4] }const stack = [1,3 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
}{ 3: [6, 7] }DFS

{ 1: [2, 3, 4] }const stack = [1,3,6 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
}{ 3: [6, 7] }{ 6: [10] }DFS

{ 1: [2, 3, 4] }const stack = [1,3,6,10]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true
}{ 3: [6, 7] }{ 6: [10] }{ 10: [] }DFS

{ 1: [2, 3, 4] }const stack = [1,3,6,10]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true
}{ 3: [6, 7] }{ 6: [10] }{ 10: [] }

DFS

{ 1: [2, 3, 4] }const stack = [1,3,6, ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true
}{ 3: [6, 7] }{ 6: [10] }

DFS

{ 1: [2, 3, 4] }const stack = [1,3 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
}{ 3: [6, 7] }DFS

{ 1: [2, 3, 4] }const stack = [1,3,7 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true
}{ 3: [6, 7] }{ 7: [] }DFS

{ 1: [2, 3, 4] }const stack = [1,3,7 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true
}{ 3: [6, 7] }{ 7: [] }

DFS

{ 1: [2, 3, 4] }const stack = [1,3 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true
}{ 3: [6, 7] }

DFS

{ 1: [2, 3, 4] }const stack = [1 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true
}DFS

{ 1: [2, 3, 4] }const stack = [1,4 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true,
4: true
}{ 4: [8] }DFS

{ 1: [2, 3, 4] }const stack = [1,4,8 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true,
4: true,
8: true
}{ 4: [8] }{ 8: [] }DFS

{ 1: [2, 3, 4] }const stack = [1,4 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true,
4: true,
8: true
}{ 4: [8] }
DFS

{ 1: [2, 3, 4] }const stack = [1 ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true,
4: true,
8: true
}
DFS

const stack = [ ]
visited = {
1: true,
2: true,
5: true,
9: true,
3: true,
6: true,
10: true,
7: true,
4: true,
8: true
}const DFS = graph => {
}
DFS
DFS - Time Complexity
Breadth First!
BFS

1
BFS

1
2
BFS

1
2
3
BFS

1
2
3
4
BFS

1
2
3
4
5
BFS

1
2
3
4
5
6
BFS

1
2
3
4
5
6
7
BFS

1
2
3
4
5
6
7
8
BFS

1
2
3
4
5
6
7
9
8
BFS

1
2
3
4
5
6
7
9
10
8


BFS
const BFS = graph => {
set start vertex to visited
load it into queue
while queue not empty
for each edge incident to vertex
if its not visited
load into queue
mark vertex
}BFS
| Order of visitation | Queue contents after processing node |
|---|---|
| S
A C D E B |
[ S ]
[ A C D E ] [ C D E B ] [ D E B ] [ E B ] [ ] |

BFS

const BFS = graph => {
initialize unexplored list
for the first vertex
add to the unexplored list
optional: store pointer to parent vertex to null
mark as visited
while unexplored list is not empty
remove next vertex from unexplored list
optional: process vertex
for each edge
if un-visited
optional: process edge
add all un-visited/explored vertices to list
optional: store pointer to parent vertex
mark as visited
mark vertex as explored
}BFS
const BFS = graph => {
}BFS

BFS - Time Complexity
What should we use BFS or DFS?
Logging or validating the contents of each edge and/or vertex.
Copying a graph, or converting between adjacency matrix or list.
Counting the number of edges and/or vertices.
Identifying the connected components.
Finding paths or cycles between two vertices.
Common tasks for BFS/DFS
const adjList = {
1:[2,5],
2:[1,5,3,4],
3:[2,4],
4:[2,5,3],
5:[4,1,2]
};
Vertices
Edges

Vertices
Edges
const adjMatrix = [
[0,1,0,0,1],
[1,0,1,1,1],
[0,1,0,1,0],
[0,1,1,0,1],
[1,1,0,1,0]
];
Directed, Undirected
Weighted, Unweighted
Self loops
Sparse, Dense
Cyclic, Acyclic
Let's find something specific


Apple
Bread
Cereal
Donut
Eggs
Fudge
Linear Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
index = 0
length = 6Linear Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
index = 1
length = 6Linear Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
index = 2
length = 6Linear Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
index = 3
length = 6Linear Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
index = 4
length = 6Linear Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
index = 4
length = 6Linear Search
Search/Find: O(n)

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 0
lastIndex = 5
mid = floor((lastIndex - firstIndex) / 2)0
5
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 0
lastIndex = 5
mid = 20
5
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 0
lastIndex = 5
mid = 2
check mid - 10
5
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 0
lastIndex = 5
mid = 2
check mid + 10
5
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 0
lastIndex = 5
mid = 2
firstIndex = mid + 10
5
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 3
lastIndex = 5
mid =
(lastIndex - firstIndex / 2)
+ firstIndex
5
3
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 3
lastIndex = 5
mid = 45
3
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 3
lastIndex = 5
mid = 45
3
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 3
lastIndex = 5
mid = 45
3
Binary Search

Apple
Bread
Cereal
Donut
Eggs
Fudge
firstIndex = 3
lastIndex = 5
mid = 45
3
Binary Search
Search/Find: O(log n)

Apple
Bread
Cereal
Donut
Eggs
Fudge
5
3
Binary vs Linear Search
O(log n)

Apple
Bread
Cereal
Donut
Eggs
Fudge
O(n)

Apple
Bread
Cereal
Donut
Eggs
Fudge
5
3
Binary vs Linear Search
O(log n)
Needs to be sorted

Apple
Bread
Cereal
Donut
Eggs
Fudge
O(n)
Unsorted

Apple
Bread
Cereal
Donut
Eggs
Fudge
5
3
Binary vs Linear Search
O(log n)
Needs to be sorted

Apple
Bread
Cereal
Donut
Eggs
Fudge
O(n)
Unsorted
What is the TC of sorting?
O(nlog(n)) *
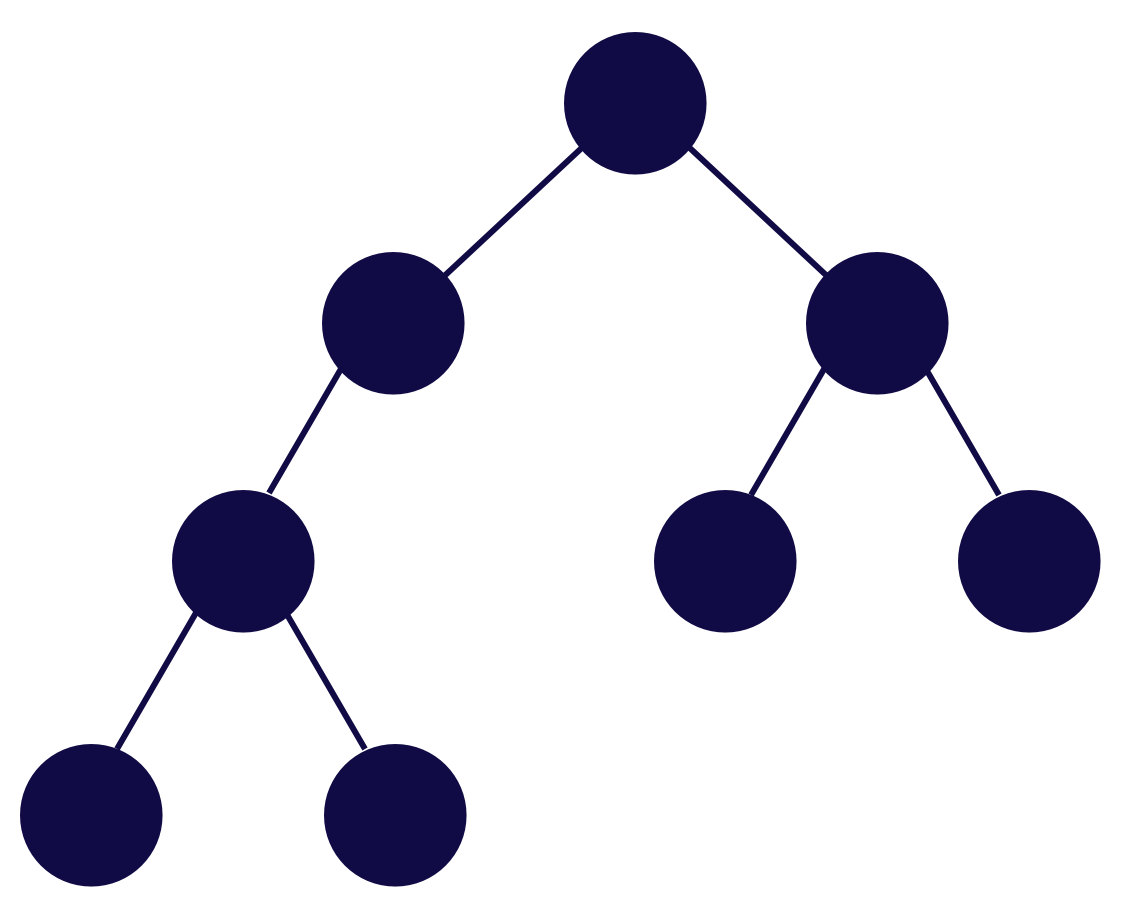
Binary Search Trees



const BST = {
root: {
value: 19,
left: {
value: 11,
left: {7},
right: {16},
},
right: {
value: 35,
left: {23},
right: null,
},
},
};
_
_
_
_
_
_
_
_
_
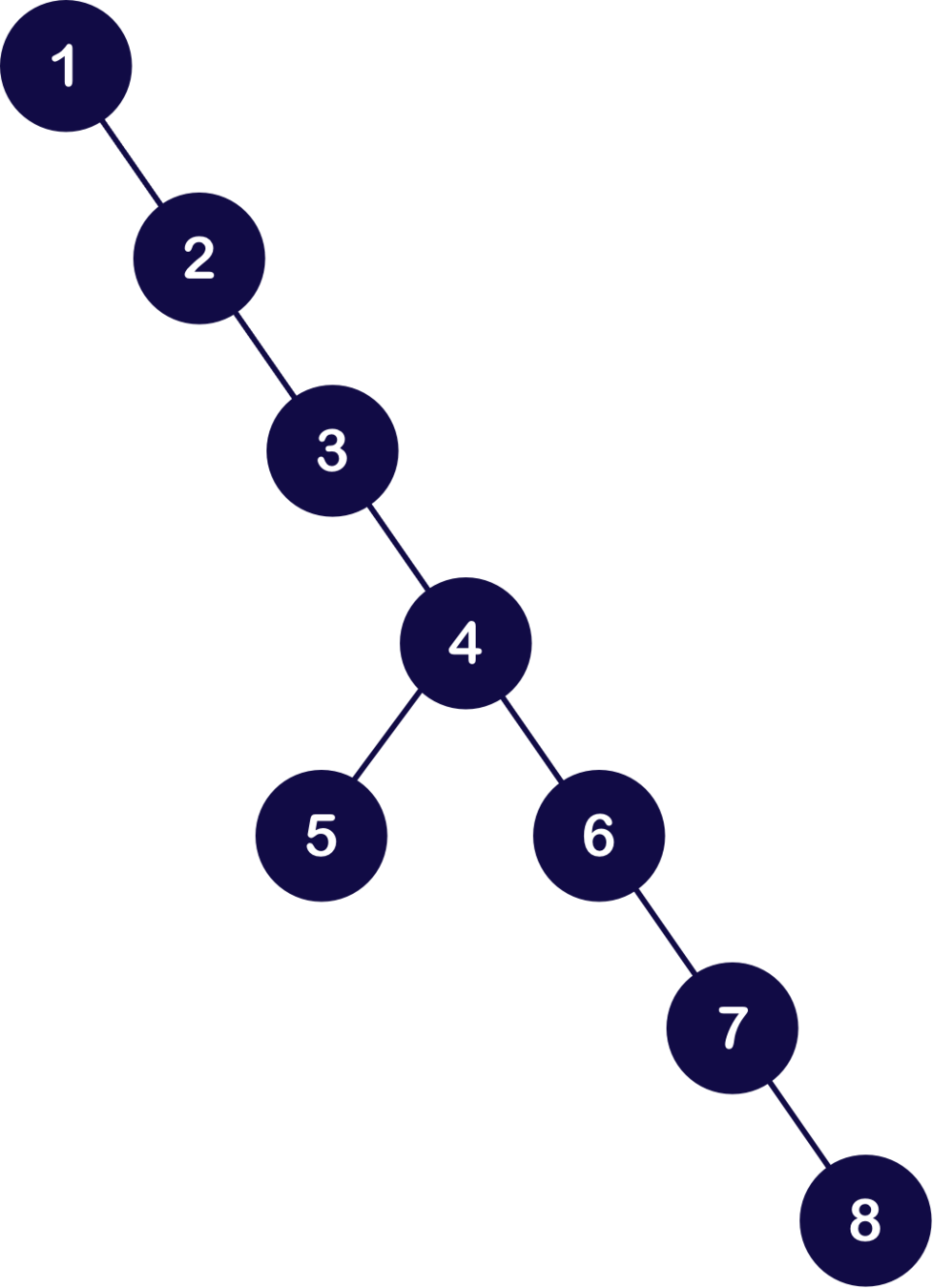
Values: 1, 2, 3, 4, 5, 6, 7, 8

_
5
7
4
8
1
6
2
3
Values: 1, 2, 3, 4, 5, 6, 7, 8
Insertion
20
?
20
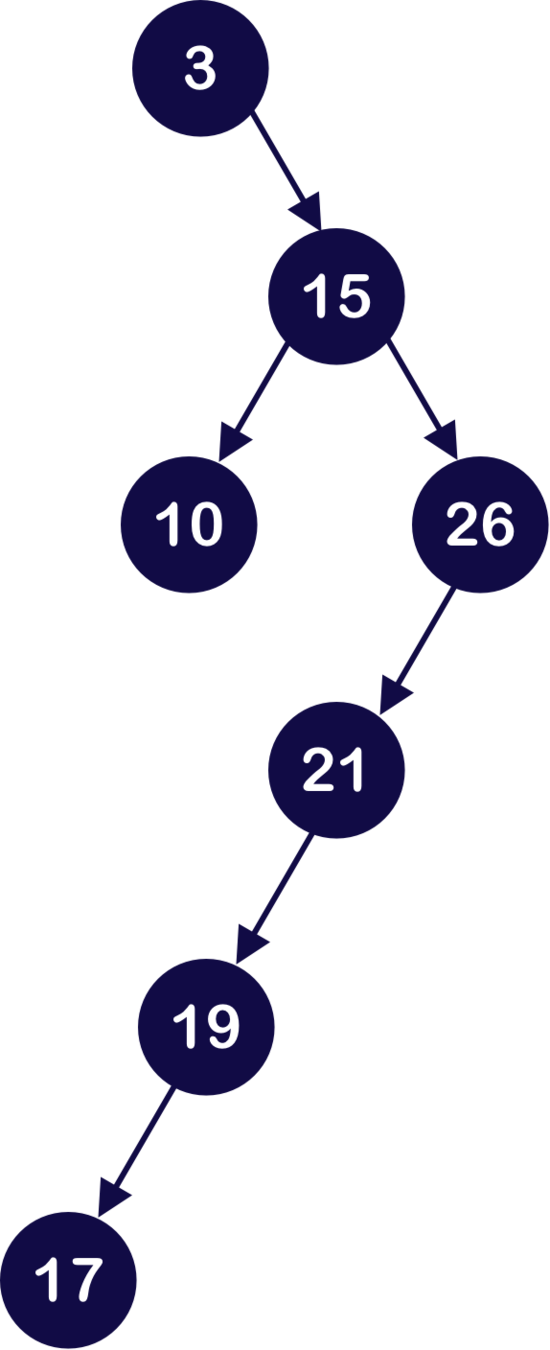
20
?
20

Insertion
20
20

Insertion
20
20

Insertion
20
20

Insertion
20
20

Insertion

20
Insertion
/** Class representing a Binary Search Tree. */
class BinarySearchTree {
constructor() {
}
/*
* Adds a new value
* @param {*} value the value to add
*/
insert(value) {
}
}
const myBST = new BinarySearchTree();
console.log(myBST)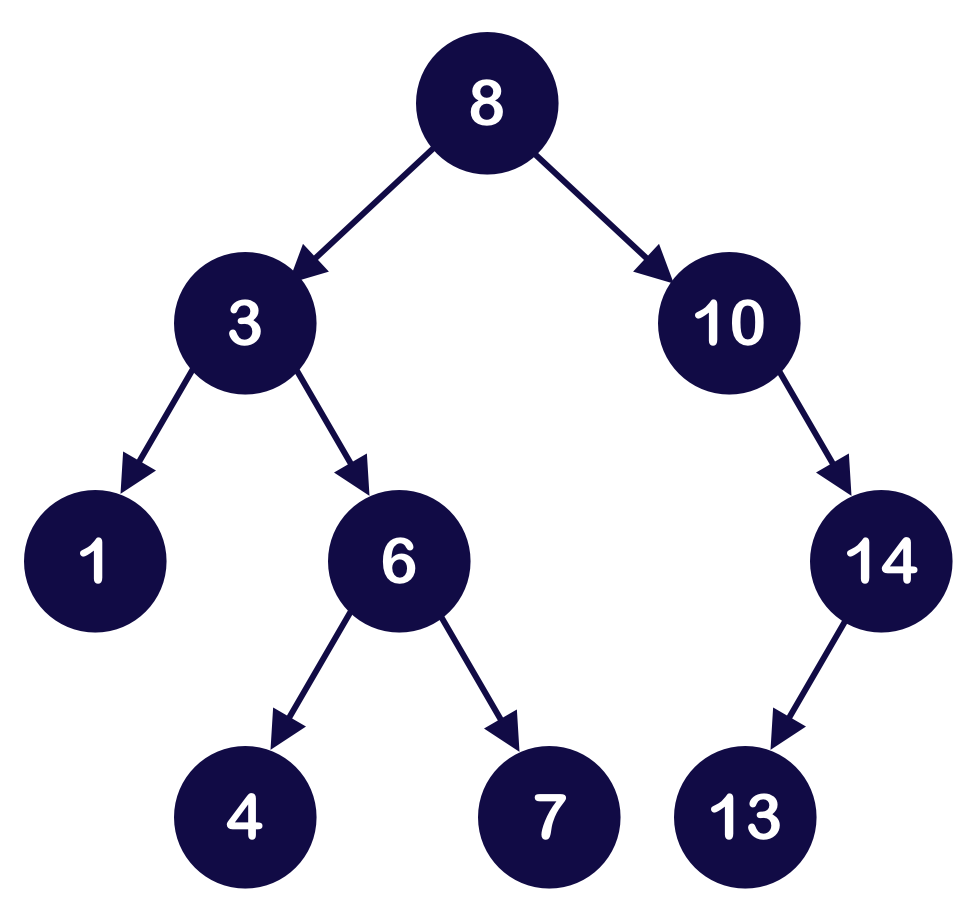
Find/Search Operation
/** Class representing a Binary Search Tree. */
class BinarySearchTree {
constructor() {
}
/*
* Searches for a value
* @param {*} value the value to find
* @returns Node
*/
contains(value) {
...
}
}
const myBST = new BinarySearchTree();
console.log(myBST)

_
5
7
4
8
1
6
2
3

Apple
Bread
Cereal
Donut
Eggs
Fudge

Apple
Bread
Cereal
Donut
Eggs
Fudge
5
3
Binary Search on Array: O(log n)
BST Search: O(h)
Linear Search on Array: O(n)

_
5
7
4
8
1
6
2
3

Apple
Bread
Cereal
Donut
Eggs
Fudge

Apple
Bread
Cereal
Donut
Eggs
Fudge
5
3
BST Insert + Delete: O(h)
Array Insert + Delete: O(n)
Compare
Don't forget about hash tables!
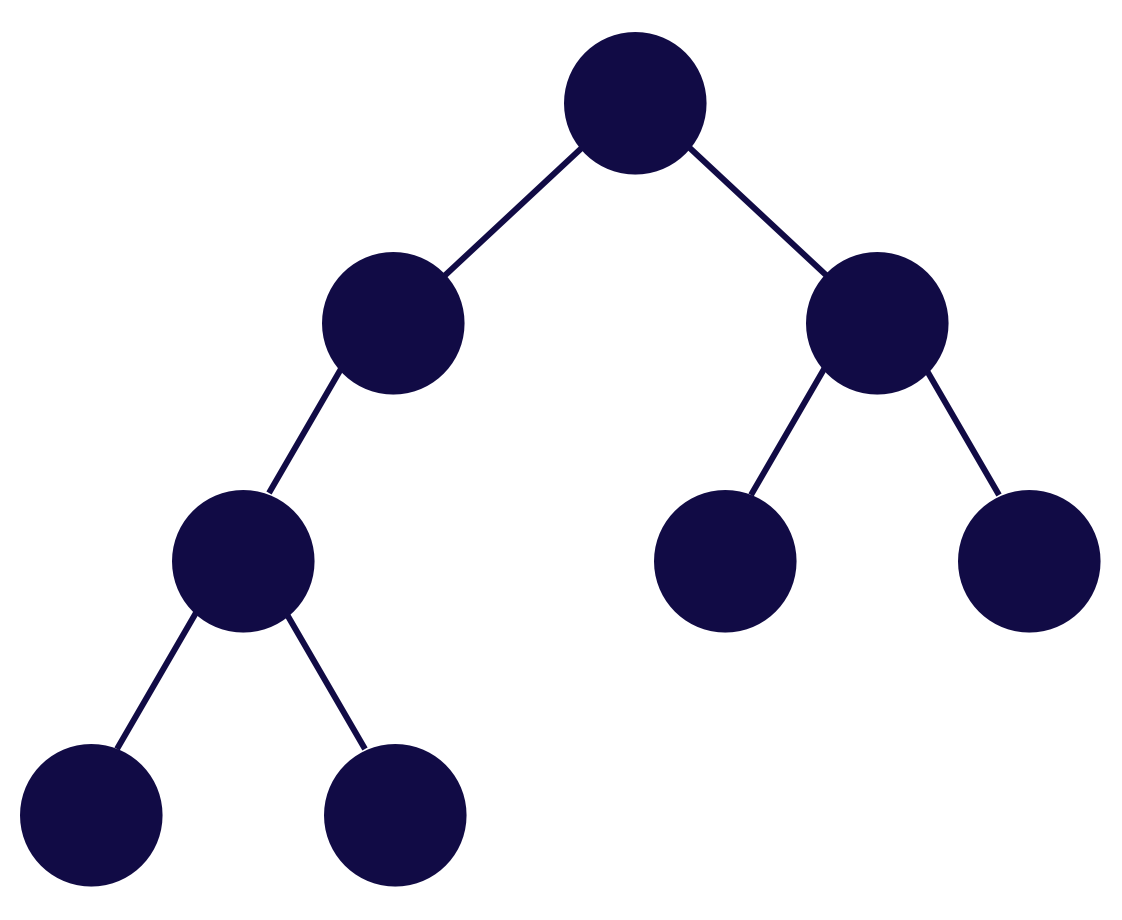
Same values, different heights
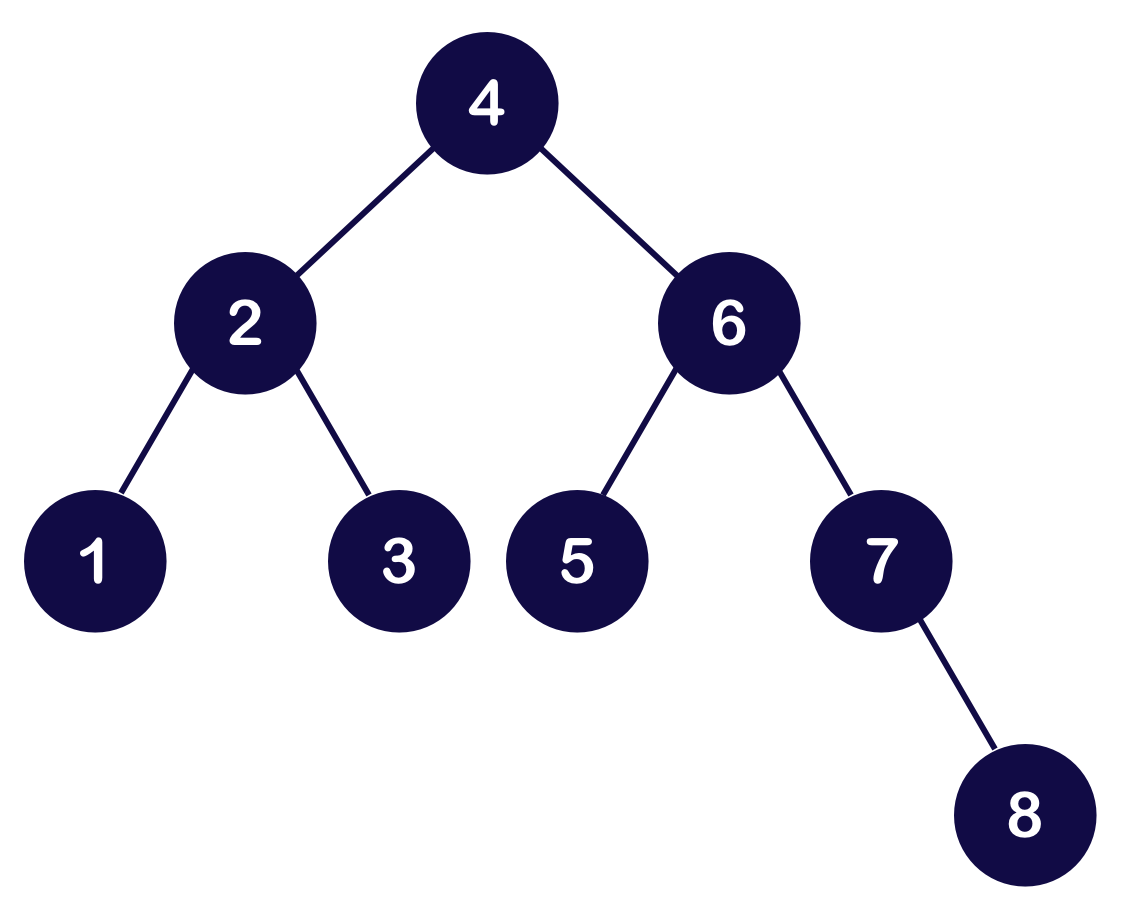



Balanced if...
1) The subtrees height differ by no more than 1
2) The left subtree is balanced
3) The right subtree of is balanced
Same values, different heights
Insert Order

Insert order: [4, 2, 1, 3, 6, 5, 7, 8]

Insert order: [1, 2, 3, 4, 5, 6, 7, 8]
Further Resources
On Frontend Masters:
Brian Holt's CS in 5hrs
Geeks for Geeks
https://github.com/jwasham/coding-interview-university
Cracking the Coding Interview
Hacker Rank / Leetcode
Interviewing.io & Pramp

A special shout out to Christopher Arriola, Jamil Lawrence, Angela Huang for all their help!
If you enjoy the comics and illustrations, follow the artists on instagram:
https://www.instagram.com/illustrationsbyem/
https://www.instagram.com/yeob_mi/