Intro to Algorithms
A Practical Introduction to Algorithms
slides.com/bgando/intro-to-algorithms
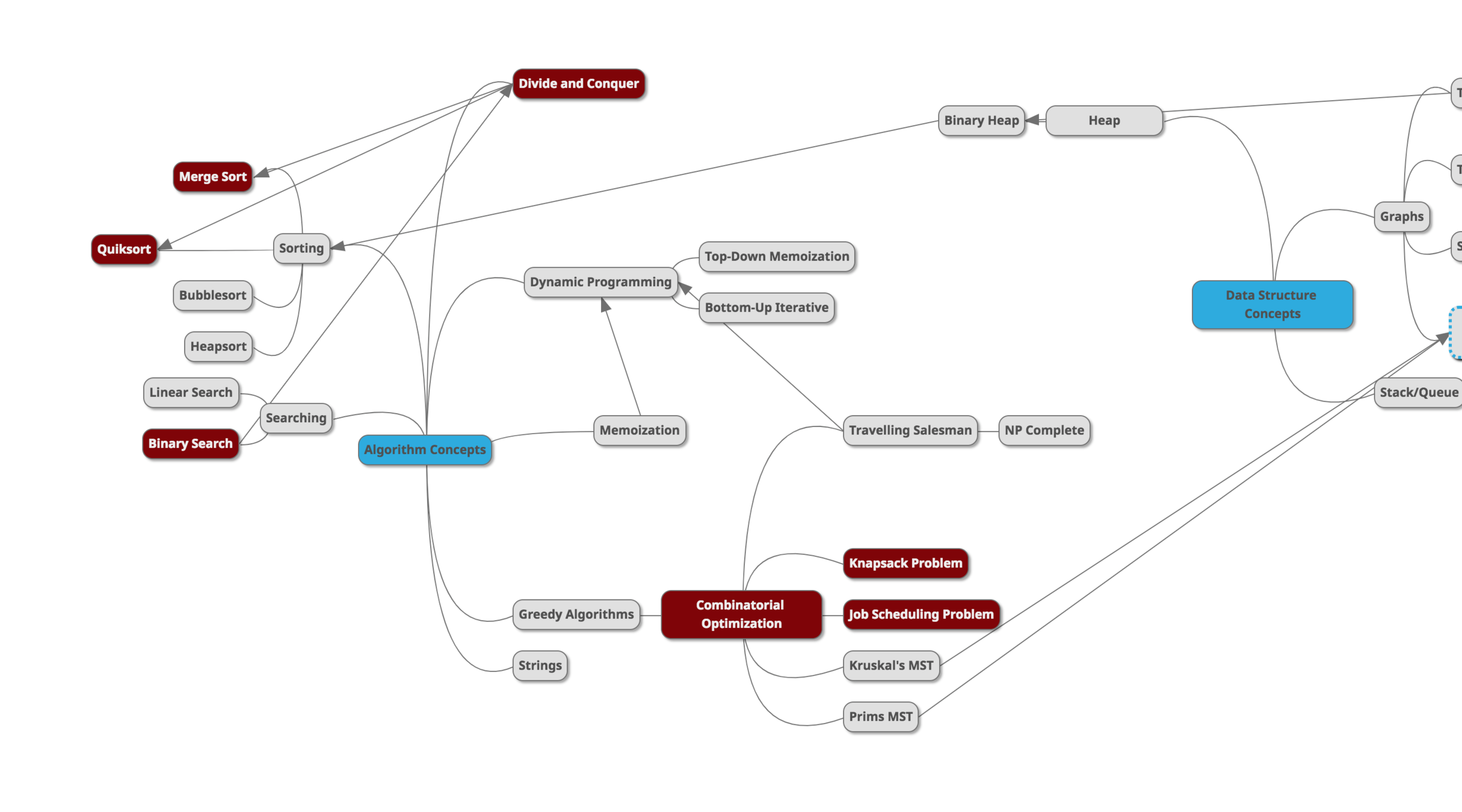
What is an algorithm?
Why should you care?
What will we cover today?
1. Estimate generally how fast an algorithm is.
2. Use some techniques to optimize certain types of algorithms.
3. Get comfortable with recursion.
4. Implement a couple sorting and searching algorithms.
5. Understand the difference between Divide & Conquer and Dynamic Programming.
6. Learn about the pros and cons of the Greedy technique.
7. Cover a recursive brute force algorithm.
That's A LOT!
You won't be able to complete all the exercises during class time, but I encourage you to take these home, practice and share your solutions with me!
Time Complexity
What makes an algorithm fast?
Time Complexity
Space Complexity
How much memory is used?
How many primitive operations are executed?
...with respect to input size
...and assuming worst case scenarios
@BIANCAGANDO
Problem:
Given a list of hotels, return the price range of hotels in a given search result.
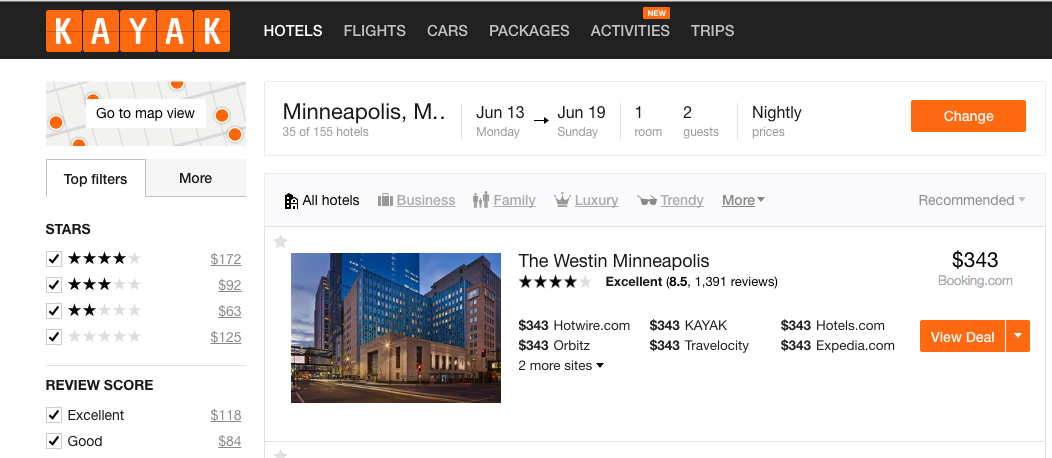
@BIANCAGANDO
@BIANCAGANDO
Problem:
Given a list of hotels, return the price range of hotels in a given search result.

@BIANCAGANDO
@BIANCAGANDO
Let's write an algorithm to do the job!

We'd expect that the more data we have, the longer it will take to figure out the min and max required for the range
However, as our dataset grows, the cost can grow really fast or slow!
@BIANCAGANDO

var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]Approach 1: compare all numbers to one another
@BIANCAGANDO
var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]| 200 | 50 | ... | 175 | |
|---|---|---|---|---|
| 200 | sdfa | |||
| 50 | adfa | |||
| ... | ||||
| 175 |
How many comparisons were made?
Approach 1: compare all numbers to one another
@BIANCAGANDO
var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]
| # of hotels (n) | 3 | 5 | 10 | 100 |
|---|---|---|---|---|
| # Ops | 9 | 15 | 100 | 1000 |
We call this n^2, where n is the number of hotels. As n grows, the amount of work increases at that rate
As our data grows, how much does our work increase?
Approach 1: compare all numbers to one another
@BIANCAGANDO
var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]| 200 | 50 | ... | 175 | |
|---|---|---|---|---|
| Max? | 200 | |||
| Min? |
How many comparisons were made?
We consider this 2n because as the data grows, the amount of work increases by 2.
Approach #2: Track min & max
@BIANCAGANDO
var hotels = [
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'},
{price: 200, brand: 'Estin'}
]
//How about if we knew the list was already sorted?How many comparisons were made?
Approach #3: Sorted List
@BIANCAGANDO
| # of Operations | Algorithm |
|---|---|
| n^2 | compare all numbers |
| 2n | Find min and max numbers |
| 2 | Sorted list, find first and last |
@BIANCAGANDO
| Big-O, name | # of Operations | Algorithm |
|---|---|---|
| O(n^2), quadratic | n^2 | compare all numbers |
| O(n), linear | 2n | Find min and max numbers |
| O(1), constant | 2 | Sorted list, find first and last |
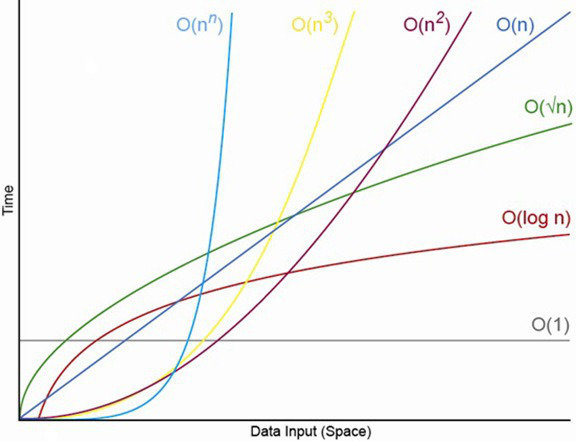
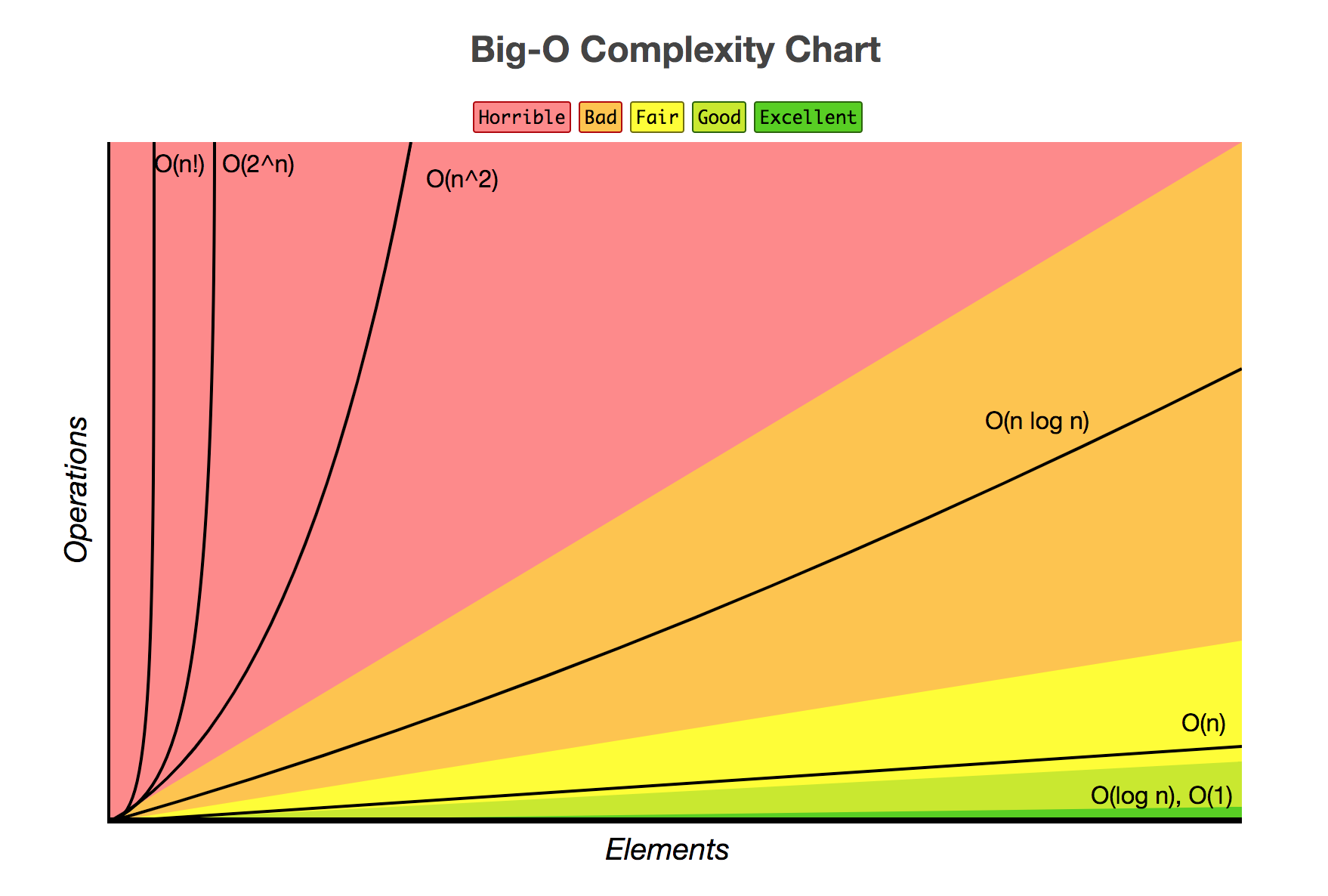
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
SUPER FAST
SUPER SLoooooW
@BIANCAGANDO
SUPER FAST
SUPER SLoooooW
@BIANCAGANDO
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
Text
Native Methods & JS Expressions
SUPER FAST
SUPER SLoooooW
//What are some simple, native JS
//methods/expressions/operations? @BIANCAGANDO
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
Text
Calculating Time Complexity
SUPER FAST
SUPER SLoooooW
What do we do if we have multiple expressions/loops/etc? @BIANCAGANDO
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
Text
Calculating Time Complexity
SUPER FAST
SUPER SLoooooW
//What about O(logn)? @BIANCAGANDO
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
Complexity of Common Operations
| Complexity | Operation |
|---|---|
| O(1) | Running a statement |
| O(1) | Value look-up on an array, object, variable |
| O(logn) | Loop that cuts problem in half every iteration |
| O(n) | Looping through the values of an array |
| O(n^2) | Double nested loops |
| O(n^3) | Triple nested loops |
@BIANCAGANDO
Given what we have discovered about time complexity, can you guess how we can calculate space complexity?
Space Complexity
@BIANCAGANDO
Time complexity of an algorithm signifies the total time required by the program to run to completion. The time complexity of algorithms is most commonly expressed using the big O notation.
Big O notation gives us an industry-standard language to discuss the performance of algorithms. Not knowing how to speak this language can make you stand out as an inexperienced programmer.
Did you know there are other notations that are typically used in academic settings? Learn more here.
@BIANCAGANDO
The complexity differs depending on the input data, but we tend to weigh the worst-case.
We graph the performance of our algorithms with one axis being the amount of data, normally denoted by 'n' and the other axis being the amount of time/space needed to execute completely.
@BIANCAGANDO
Worst-case scenario, dropping any non-significant operations or constants.
Big 'O' Notation

@BIANCAGANDO
Break Time!
What is the TC?
var countChars = function(str){
var count = 0;
for(var i = 0; i < str.length; i++) {
count++;
}
return count;
};
countChars("dance");
countChars("walk"); @BIANCAGANDO
var countChars = function(str){
return str.length;
};
countChars("dance");
countChars("walk");
// How much more work would it take
// to get the length of 1 million
//char string? @BIANCAGANDO
What is the TC?
What is the TC?
var myList = ["hello", "hola"];
myList.push("bonjour");
myList.unshift();
//calculate the time complexity for the
//native methods above (separately) @BIANCAGANDO
Faster Algorithms!
Time Complexity?
@BIANCAGANDO
We can do better!
@BIANCAGANDO
Your Turn
@BIANCAGANDO
Solution
@BIANCAGANDO
Memoization
Memoization: caching the value that a function returns
const factorial = (n) => {
// Calculations: n * (n-1) * (n-2) * ... (2) * (1)
return factorial;
}
factorial(35);
@BIANCAGANDO
Memoization
Memoization: caching the value that a function returns
const factorial = (n) => {
// Calculations: n * (n-1) * (n-2) * ... (2) * (1)
return factorial;
}
factorial(35);
factorial(36); // factorial(36) = factorial(35) * 36; @BIANCAGANDO
Exercise 1
@BIANCAGANDO
Memoization
Exercise 2
@BIANCAGANDO
Exercise 3
@BIANCAGANDO
Solutions
@BIANCAGANDO
Recursion
RECURSION
Recursion is simply when a function calls itself; however it doesn't stop there.

@BIANCAGANDO
WHY RECURSION?
Elegant solutions to keep your code D.R.Y.
Expected CS knowledge
var callMe = function() {
callMe();
callMe();
callMe("anytime");
}; @BIANCAGANDO

@BIANCAGANDO
Call Stack Game
1. Push called Fn on stack.
2. Execute Fn body.
until...
... another fn is called:
Pause the current execution and start at step 1.
... a return is hit:
Pop the current Fn off the stack.
Resume executing the previous Fn.
var callMe = function() {
callMe();
callMe();
callMe('anytime');
}; @BIANCAGANDO
What is this doing?
var tracker = 0;
var callMe = function() {
tracker++
if (tracker === 3) {
return 'loops!';
}
callMe('anytime');
};Call Stack Game
@BIANCAGANDO
1. Push called Fn on stack.
2. Execute Fn body.
until...
... another fn is called:
Pause the current execution and start at step 1.
... a return is hit:
Pop the current Fn off the stack.
Resume executing the previous Fn.
Recursion in 4 Steps
var callMyself = function() {
if() {
// base case
return;
} else {
// recursive case
callMyself();
}
return;
};1. Identify base case(s).
2. Identify recursive case(s).
3. Return where appropriate.
4. Write procedures for each case that bring you closer to the base case(s).
@BIANCAGANDO
LOOPING
@BIANCAGANDO
FACTORIAL WITH LOOP
@BIANCAGANDO
FACTORIAL WITH LOOP
function computeFactorial(num) {
var result = 1;
for(var i = 2; i <= num; i++) {
result *= i;
}
return result;
}results *= 2;
results *= 3;
results *= 4;
results *= 5;If we call computeFactorial(5), then the loop will run:
What pattern do you notice?
@BIANCAGANDO
WITH RECURSION
@BIANCAGANDO
LOOP TO RECURSION
@BIANCAGANDO
RECURSIONS vs LOOPS
Recursion can always be implemented as a loop, but in some situations, believe it or not, it is simpler to use recursion
ES6 offers TCO, which allows some functions to be called without growing the call stack.
Read more here and here.
Tail-Call
Optimization
@BIANCAGANDO
COMMON PATTERNS
FOR RECURSION
-
Wrapper Functions
-
Accumulators

@BIANCAGANDO
WRAPPER FUNCTIONS
@BIANCAGANDO
ACCUMULATORS
@BIANCAGANDO
EXERCISE
@BIANCAGANDO
SOLUTION
@BIANCAGANDO
Exercise
@BIANCAGANDO
Solution
@BIANCAGANDO
Divide and Conquer
Binary Search
Binary Search
Search for a value in a sorted array by cutting the side of the search area in half.
@BIANCAGANDO
Linear Search

Linear Search
Search for a value in an array by checking each value in order.
@BIANCAGANDO
Exercise 1
@BIANCAGANDO
Exercise 2
@BIANCAGANDO
Divide and Conquer
0. Recognize base case
1. Divide: Break problem down during each call
2. Conquer: Do work on each subset
3. Combine: Solutions
Recursive calls to a subset of the problem
@BIANCAGANDO
Naive Sorts
Keep looping and comparing values until the list is sorted
Divide & Conquer Sorts
Recursively divide lists and sort smaller parts of list until entire list is sorted
Bubble Sort
Insertion Sort
Selection Sort
Mergesort
Quiksort
Comparison Sorts
@BIANCAGANDO
BUBBLE SORT
Bubble Sort
Loop through an array, comparing adjacent indices and swapping the greater value to the end

@BIANCAGANDO
MERGESORT
Merge Sort
Recursively merge sorted sub-lists.

@BIANCAGANDO
The merge step takes two sorted lists and merges them into 1 sorted list.
Concept: Merging Lists
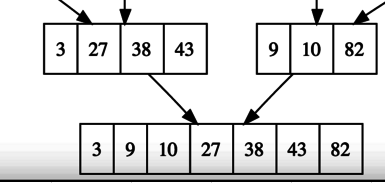
9
10
27
38
43
82
X
X
X
X
X
X
X
@BIANCAGANDO
@BIANCAGANDO
Pseudocode: Merge Routine
merge(L,R) @BIANCAGANDO
Concept: Merge Sort
Step 1:
Divide input array into 'n' single element subarrays
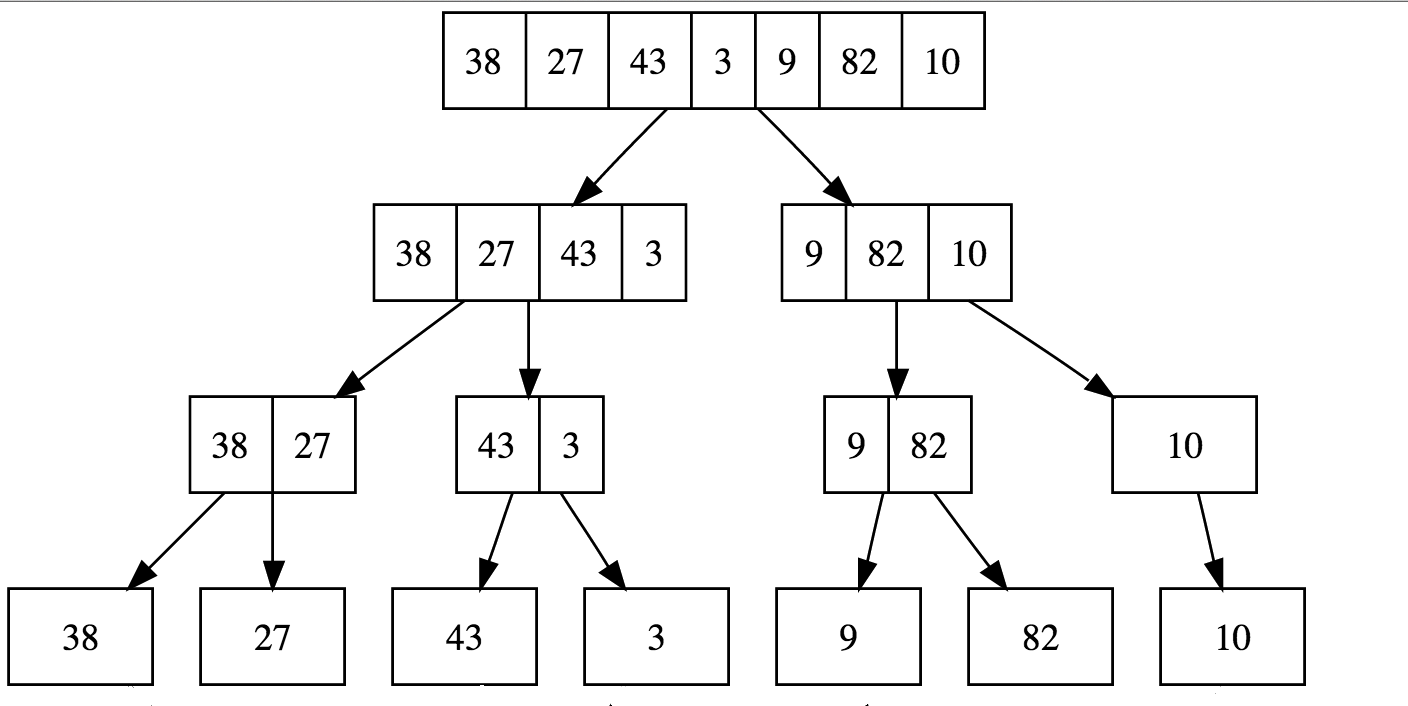
@BIANCAGANDO
Step 2:
Repeatedly merge subarrays and sort on each merge
Concept: Merge Sort
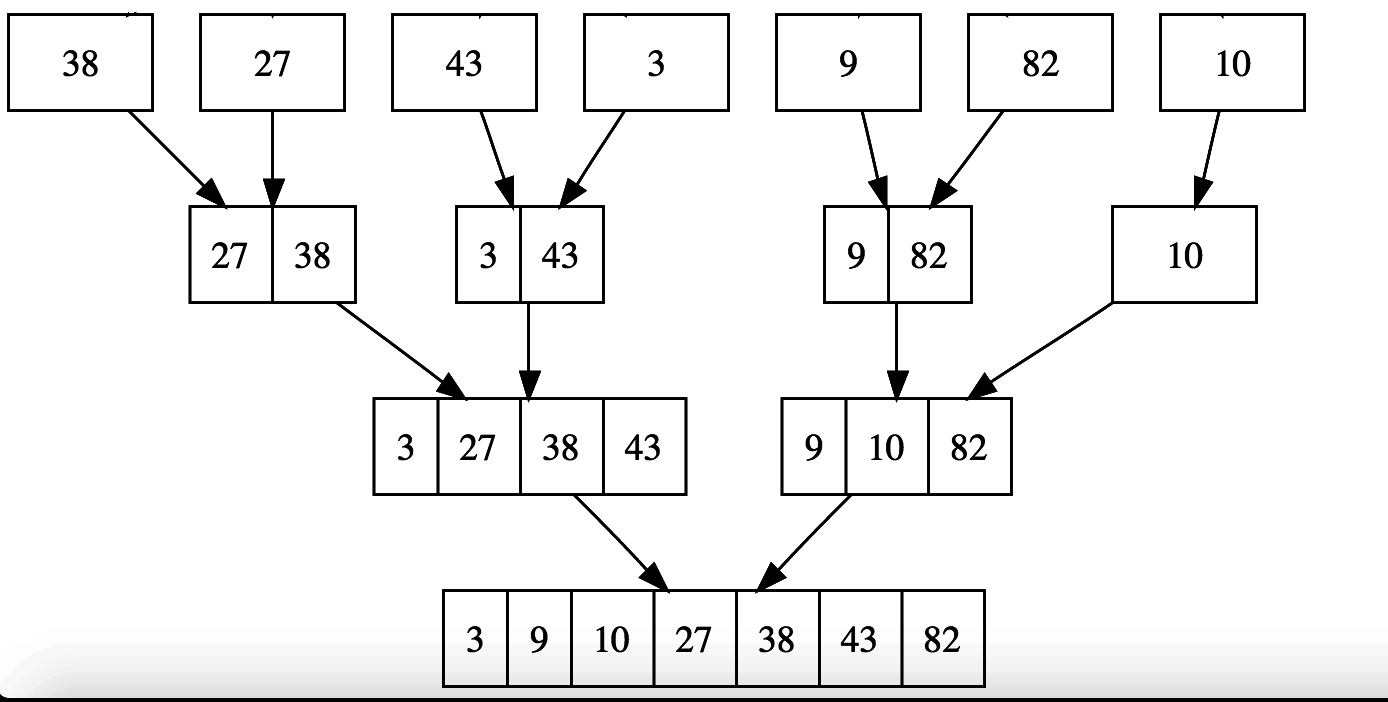
@BIANCAGANDO
Concept: Merge Sort
interactive visualizations here
https://www.youtube.com/watch?v=XaqR3G_NVoo
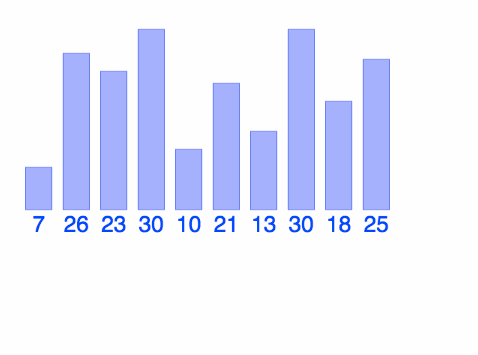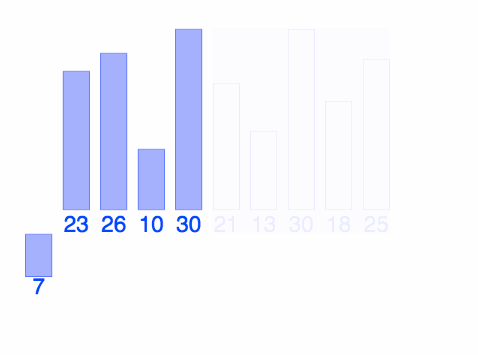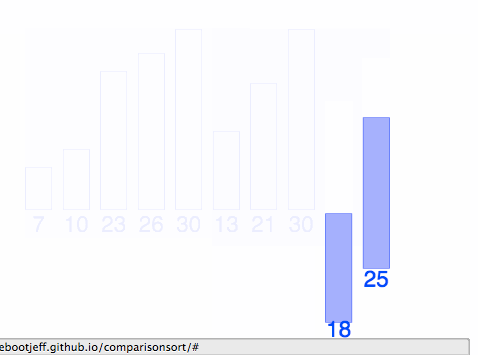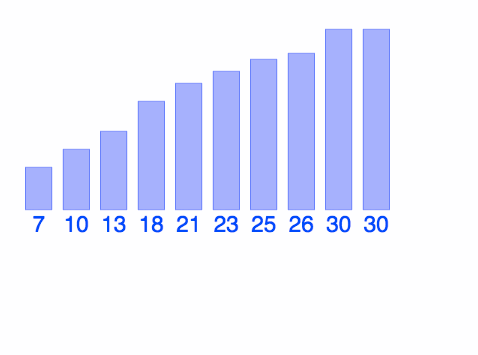
@BIANCAGANDO
Pseudocode: Merge Sort
mergeSort(list)
base case: if list.length < 2, return
break the list into halves L & R
Lsorted = mergeSort(L)
Rsorted = mergeSort(R)
return merge(Lsorted, Rsorted)
@BIANCAGANDO
Text
Pseudocode: Merge Sort
mergeSort(list)
initialize n to the length of the list
base case is if n < 2, just return
initialize mid to n/2
left = left slice of array to mid - 1
right = right slice of array mid to n - 1
mergeSort(left)
mergeSort(right)
merge(left, right) @BIANCAGANDO
Text
Simplified Analysis
mergeSort(list)
initialize n to the length of the list
base case is if n < 2, just return
initialize mid to n/2
left = left slice of array to mid - 1
right = right slice of array mid to n - 1
mergeSort(left)
mergeSort(right)
merge(left, right, a)


constant
N/A
linear

n/2
O(n*logn)
@BIANCAGANDO
@BIANCAGANDO
Exercise 1 - Bubblesort
@BIANCAGANDO
Exercise 2 - MergeSort
@BIANCAGANDO
Solution - Bubblesort
@BIANCAGANDO
Solution - Mergesort
@BIANCAGANDO
Greedy Algorithms
Text
@BIANCAGANDO
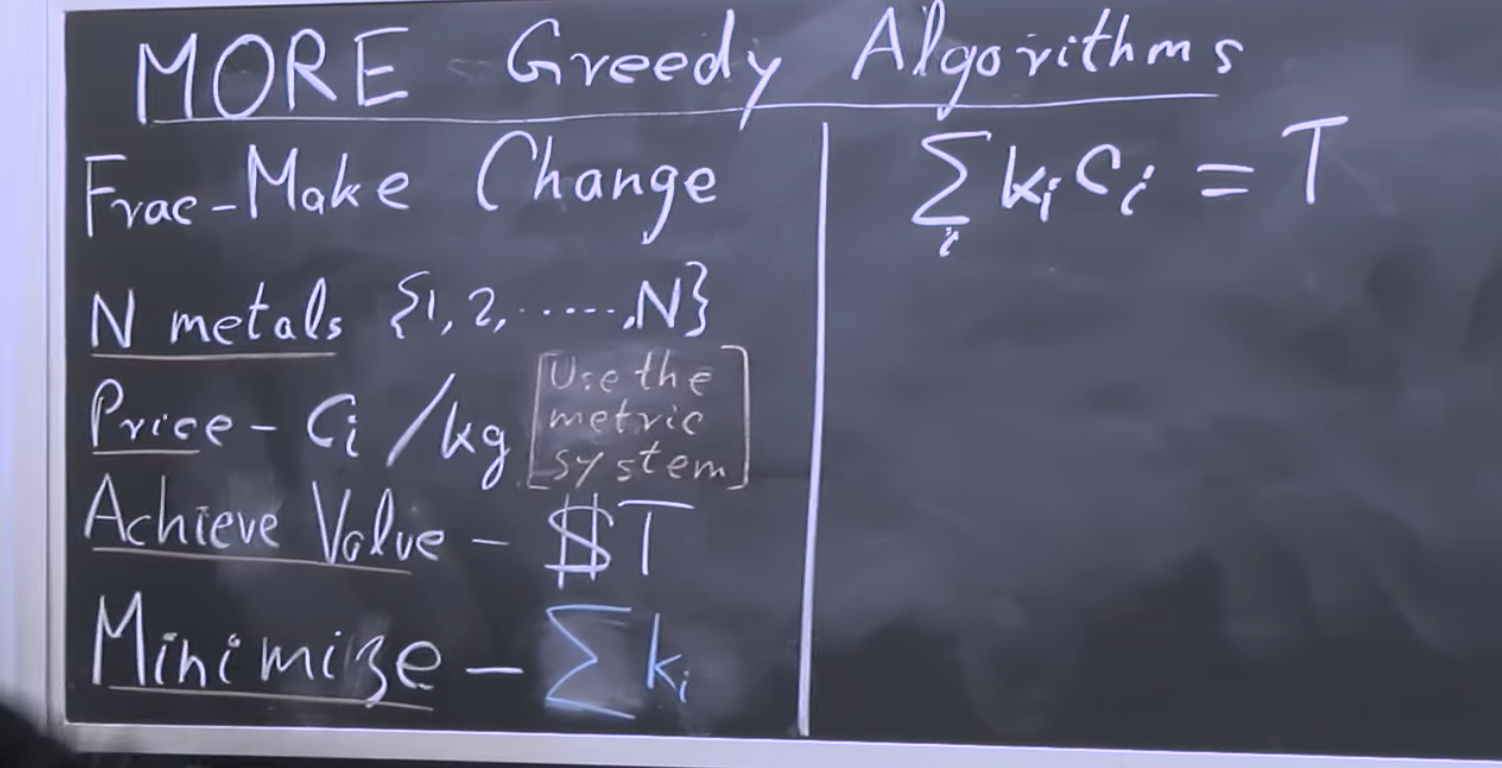
Text
@BIANCAGANDO
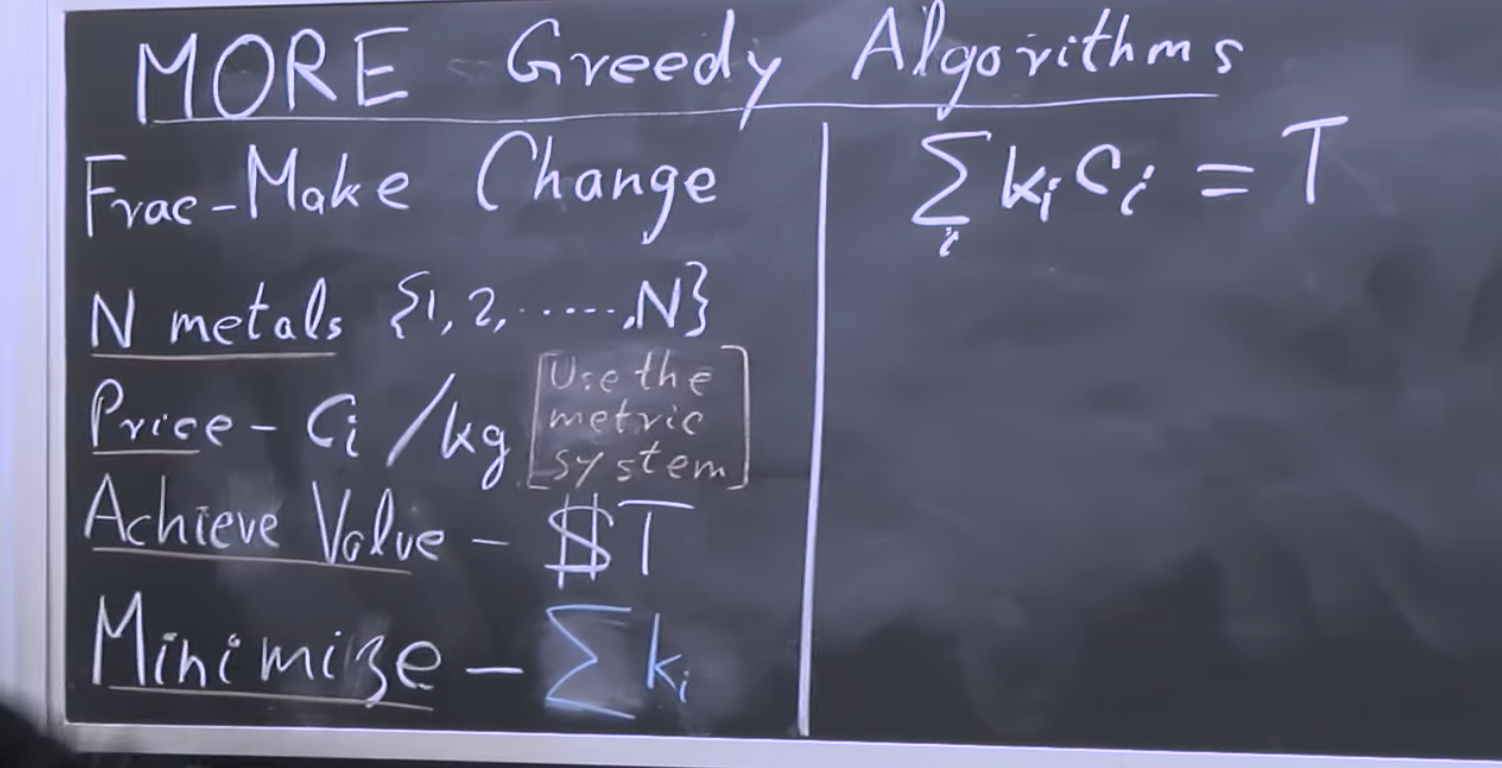

@BIANCAGANDO
Greedy Approach
Greedy algorithms always make the locally optimal choice!
@BIANCAGANDO
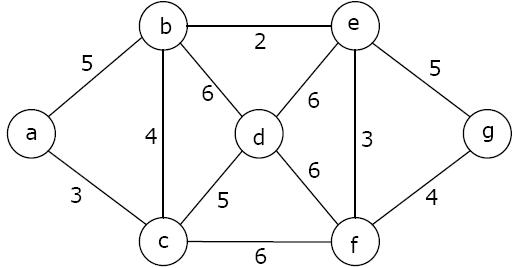
Locally Optimal Solution
@BIANCAGANDO

Locally Optimal Solution
Total: 3 + 4 + 2 + 3 + 4
16!
@BIANCAGANDO

Locally Optimal Solution
Total: 12
@BIANCAGANDO
You are the banker in Monopoly with your family who has lost many of the game pieces so you only have bills in these denominations:
$5 $10 $25
You need only pay out your family in the least number of bills possible so you don't run out before the game is over. Write a function that calculates the least number of bills required for any given dollar amount that is divisible by 5.
@BIANCAGANDO
Greedy Approach
Write a function, makeChange, that returns the least number of coins that add up to that amount.
coin values: 5, 10, 25
input: 40 , output: 3 (25, 10, 5)
input: 35, output 2 (25, 10)
Exercise
@BIANCAGANDO
Greedy Approach
Write a function, makeChange, that returns the least number of coins that add up to that amount.
coin values: 5, 10, 25
input: 40 , output: 3 (25, 10, 5)
input: 35, output 2 (25, 10)
SOLUTION
@BIANCAGANDO
Would these values work with your greedy solution?
coin values: 1, 6, 10
input: 12
Greedy Approach:
Always subtract the largest coin possible from the current amount.
const makeChange = (coins, amount) => {
coins.sort((a, b) => b - a);
let coinTotal = 0;
let i = 0;
while (amount > 0) {
if (coins[i] <= amount) {
amount -= coins[i];
coinTotal++;
} else {
i++;
}
}
return coinTotal;
};
makeChange([1, 6, 10], 12); @BIANCAGANDO
Would these values work with your greedy solution?
coin values: 1, 6, 10
input: 12
Algorithmic Correctness
Does your algorithm correctly solve the problem?
const makeChange = (coins, amount) => {
coins.sort((a, b) => b - a);
let coinTotal = 0;
let i = 0;
while (amount > 0) {
if (coins[i] <= amount) {
amount -= coins[i];
coinTotal++;
} else {
i++;
}
}
return coinTotal;
};
makeChange([1, 6, 10], 12); @BIANCAGANDO
Brute Force Algorithms
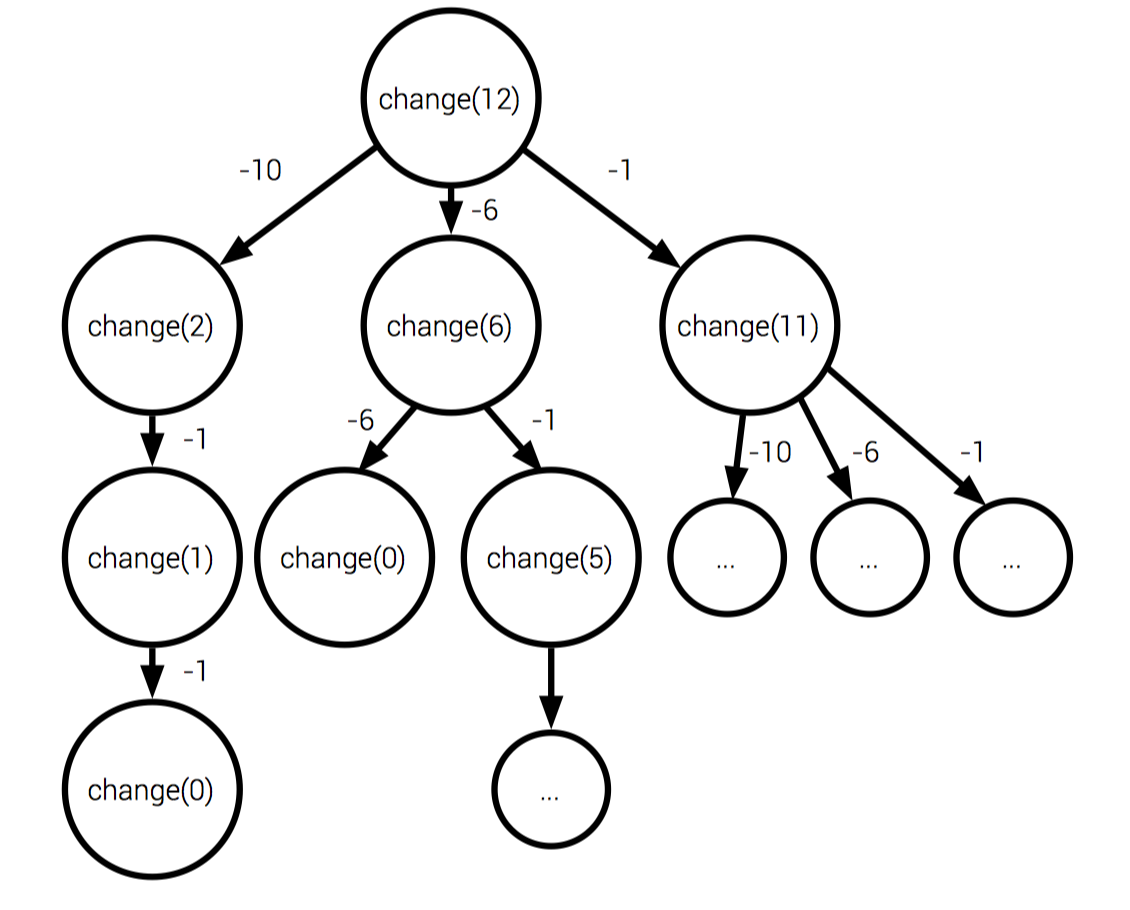
Brute Force Approach:
Calculate every single combination possible and keep track of the minimum.
@BIANCAGANDO
BRUTE FORCE
Dynamic Programming
@BIANCAGANDO
DYNAMIC PROGRAMMING
@BIANCAGANDO
DYNAMIC PROGRAMMING
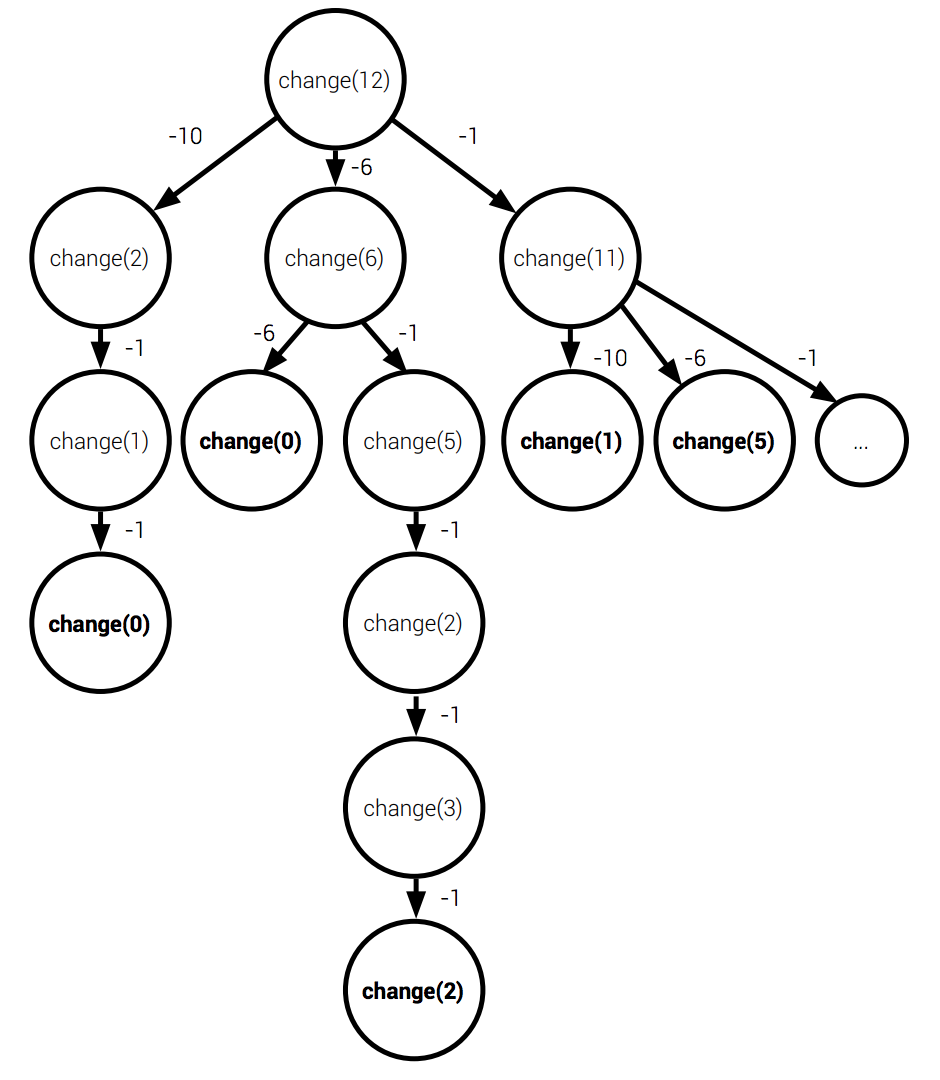
Dynamic Approach:
Cache values to avoid repeated calculations
@BIANCAGANDO
DYNAMIC PROGRAMMING
DP Qualities:
Optimal Substructure (tends to be recursive)
Overlapping Subproblems
DP vs Divide & Conquer
DP Approaches:
Top Down (recursive) vs Bottom Up (iterative)
@BIANCAGANDO
Top- Down Memoization

Bottom-Up Iterative

@BIANCAGANDO
Memoization + Recursive Approach
@BIANCAGANDO
Exercise
@BIANCAGANDO
Solution