Text
@BiancaGando

Intro to
Time Complexity
What makes an algorithm "fast"?
Evaluating Sorting Algorithms:
Complexity
Time Complexity
Space Complexity
How much memory is used?
How many comparisons are made?
How many swaps are made?
...with respect to input size
...and assuming worst case scenarios
@BiancaGando

@BiancaGando

Let's imagine that you work for Kayak.com and were asked to add a feature that listed the price range of hotels in a given area.
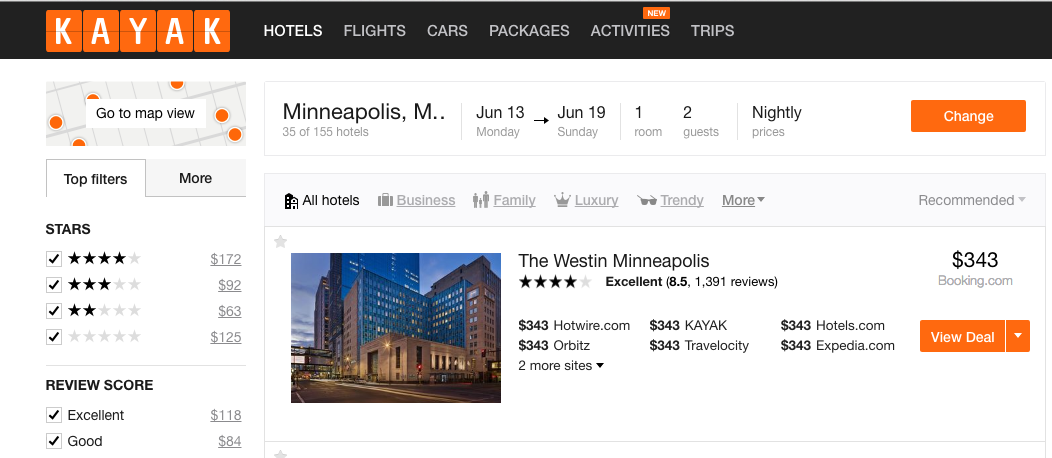
@BiancaGando

Let's write an algorithm to do the job!

We'd expect that the more data we have, the longer it will take to figure out the min and max required for the range
However, as our dataset grows, the cost can grow really fast or slow!
@BiancaGando


var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]@BiancaGando

var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]
//Let's see how much work it would take to
//compare all numbers to find the min/max in this list| 200 | 50 | ... | 175 | |
|---|---|---|---|---|
| 200 | ||||
| 50 | ||||
| ... | ||||
| 175 |
How many comparisons were made?
@BiancaGando

var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]
//Let's see how much work it would take to
//compare all numbers to find the min/max in this list| n | 3 | 5 | 10 | 100 |
|---|---|---|---|---|
| # Ops |
We call this n^2 because as n grows, the amount of work increases at that rate
As our data grows, how much does our work increase?
@BiancaGando

var hotels = [
{price: 200, brand: 'Estin'},
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'}
]
//What if we just checked if the item was the min or max?| 200 | 50 | ... | 175 | |
|---|---|---|---|---|
| Max? | ||||
| Min? |
How many comparisons were made?
We consider this 2n because as the data grows, the amount of work increases by 2.
@BiancaGando

var hotels = [
{price: 50, brand: 'Best Eastern'},
...
...
{price: 175, brand: 'Radishin'},
{price: 200, brand: 'Estin'}
]
//How about if we knew the list was already sorted?How many comparisons were made?
@BiancaGando

| # of Operations | Algorithm |
|---|---|
| n^2 | compare all numbers |
| 2n | Find min and max numbers |
| 3 | Sorted list, find first and last |
@BiancaGando

| Big-O, name | # of Operations | Algorithm |
|---|---|---|
| O(n^2), quadratic | n^2 | compare all numbers |
| O(n), linear | 2n | Find min and max numbers |
| O(1), constant | 3 | Sorted list, find first and last |
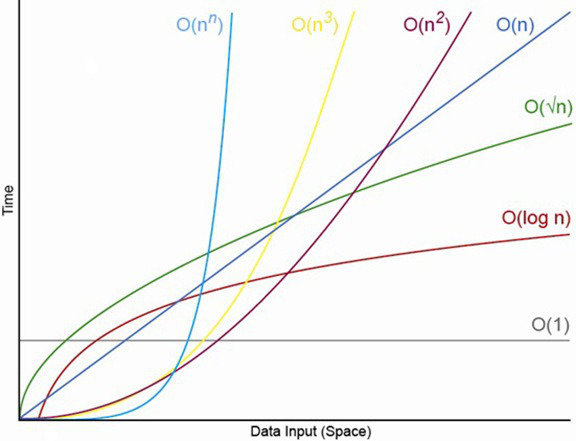
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
SUPER FAST
SUPER SLoooooW
@BiancaGando

| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
SUPER FAST
SUPER SLoooooW
@BiancaGando

Calculating Time Complexity
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
SUPER FAST
SUPER SLoooooW
//What are some simple, native JS methods/expressions/operations?@BiancaGando

Calculating Time Complexity
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
SUPER FAST
SUPER SLoooooW
What do we do if we have multiple expressions/loops/etc?@BiancaGando

Calculating Time Complexity
| Name | constant | logarithmic | linear | quadratic | exponential |
| Notation | O(1) | O(logn) | O(n) | O(n^2) | O(k^n) |
SUPER FAST
SUPER SLoooooW
//What about O(logn)?@BiancaGando

Complexity of Common Operations
| Complexity | Operation |
|---|---|
| O(1) | Running a statement |
| O(1) | Value look-up on an array, object, variable |
| O(logn) | Loop that cuts problem in half every iteration |
| O(n) | Looping through the values of an array |
| O(n^2) | Double nested loops |
| O(n^3) | Triple nested loops |
@BiancaGando

Given what we have discovered about time complexity, can you guess how we can calculate Space Complexity?
Space Complexity
@BiancaGando

Time complexity of an algorithm signifies the total time required by the program to run to completion. The time complexity of algorithms is most commonly expressed using the big O notation.
Big O notation gives us an industry-standard language to discuss the performance of algorithms. Not knowing how to speak this language can make you stand out as an inexperienced programmer.
Did you know there are other notations that are typically used in academic settings? Learn more here.
Review: Time Complexity
@BiancaGando

The complexity differs depending on the input data, but we tend to weigh the worst-case.
We graph the performance of our algorithms with one axis being the amount of data, normally denoted by 'n' and the other axis being the amount of time/space needed to execute completely.
Review: Time Complexity
@BiancaGando

Worst-case scenario, dropping any non-significant operations or constants.
Big 'O' Notation

Exercise Time!
@BiancaGando

@BiancaGando

What is the TC?
var countChars = function(str){
var count = 0;
for(var i = 0; i < str.length; i++){
count++;
}
return count;
};
countChars("dance");
countChars("walk");@BiancaGando

What is the TC?
var countChars = function(str){
return str.length;
};
countChars("dance");
countChars("walk");
//How much more work would it take to get the
//length of 1 million char string?@BiancaGando

What is the TC?
var myList = ["hello", "hola"];
myList.push("bonjour");
myList.unshift();
//calculate the time complexity for the
//native methods above (separately)@BiancaGando

Intro to
Elementary Sorting
Bubble, Insertion, Selection
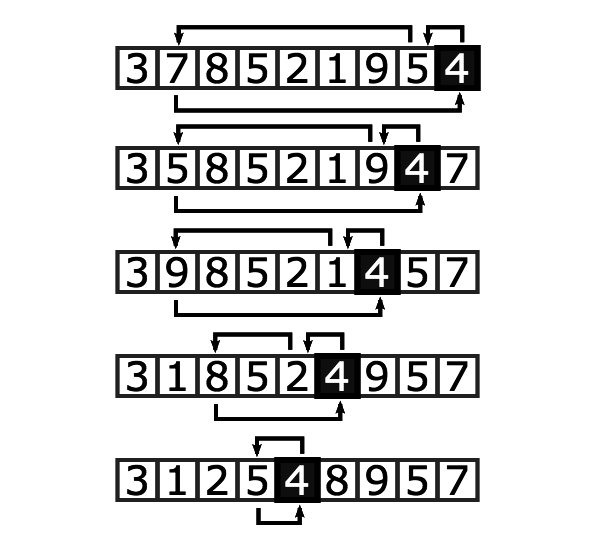
Concept: Bubble Sort
@BiancaGando

is a comparison sort that repeatedly swaps adjacent elements that are out of order
values 'bubble up' to the top of the data structure
Diagram: Bubble Sort
Check out the Interactive Visualization
https://www.youtube.com/watch?v=lyZQPjUT5B4
@BiancaGando

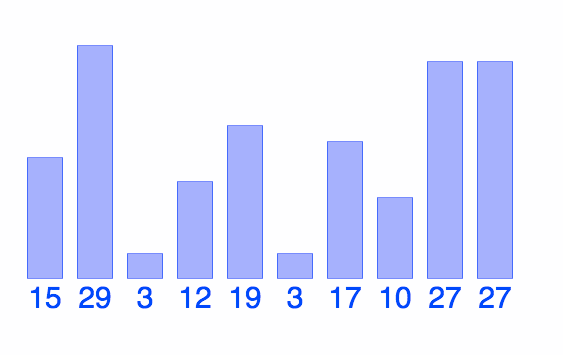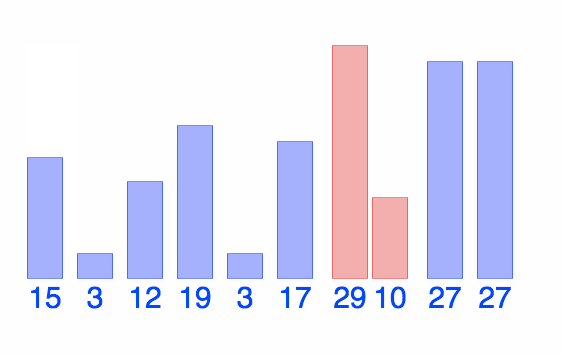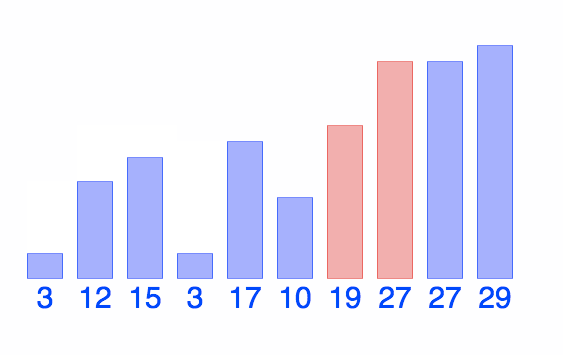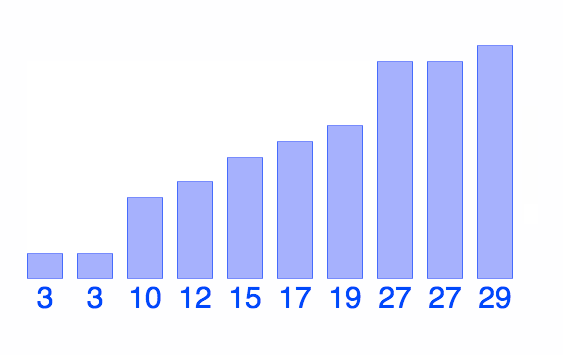
@BiancaGando

1. Sorting Function
bubbleSort(list) -> a sorted list
loops through list
compares adjacent elements
swaps higher item towards the end
How is this different from implementing data structures yesterday?
Interface: Bubble Sort
@BiancaGando

Pseudocode: Bubble Sort
bubbleSort(list)@BiancaGando

Pseudocode: Bubble Sort
//bubbleSort(list)
//for k, loop through 1 to n-1
//for i loop 0 to n-2
//if A[i] is greater than A[i+1]
//swap A[i] with A[i+1]
@BiancaGando

Analysis: Bubble Sort
//bubbleSort(list)
//for k, loop through 1 to n-1
//for i loop 0 to n-2
//if A[i] is greater than A[i+1]
//swap A[i] withA[i+1]
constant
n-1
n-1
F(n) = (n-1) * (n-1) * c
F(n) = c(n^2) - 2cn + 1
What is the highest order of this polynomial?
@BiancaGando

Optimize: Bubble Sort
//bubbleSort(list)
//for k, loop through 1 to n-k-1
//for i loop 0 to n-2
//if A[i] is greater than A[i+1]
//swap A[i] withA[i+1]
constant
n-1
n-k-1
We don't need to loop all the way to the end every time because the right side of the array becomes sorted every loop
@BiancaGando

Optimize: Bubble Sort
//bubbleSort(list)
//for k, loop through 1 to n-k-1
//for i loop 0 to n-2
//if A[i] is greater than A[i+1]
//swap A[i] withA[i+1]
constant
n-1
n-k-1
What if we go through one iteration through the list without swapping?
@BiancaGando

O(n^2)
Time Complexity
O(1)
Space Complexity
Break Time!
@BiancaGando

Evaluating Sorting Algorithms:
Stability
A sorting algorithm is stable if it
preserves the order of equal items.
@BiancaGando

Note: Any comparison-based sorting algorithm can be made stable by using position as a criteria when two elements are compared.
Evaluating Sorting Algorithms:
Stability (example)
Prompt: I want bikes sorted by price (ascending). Given equal prices, I want lighter option to be first.
The list is already sorted by weight (ascending). I just need to sort it by price. But an unstable sort based on price could "unsort" weights.
| Bike A | $600 | 20 lbs. |
| Bike B | $500 | 30 lbs. |
| Bike C | $500 | 35 lbs. |
@BiancaGando

Evaluating Sorting Algorithms:
Stability (example)
Prompt: I want bikes sorted by price (ascending). Given equal prices, I want lighter option to be first.
The list is already sorted by weight (ascending). I just need to sort it by price. But an unstable sort based on price could "unsort" weights.
| Bike A | $600 | 20 lbs. |
| Bike B | $500 | 30 lbs. |
| Bike C | $500 | 35 lbs. |
@BiancaGando

| Bike B | $500 | 30 lbs. |
| Bike C | $500 | 35 lbs. |
| Bike A | $600 | 20 lbs. |
Evaluating Sorting Algorithms:
Adaptability
A sorting algorithm is "adaptive"
if it becomes more efficient
(i.e., if its complexity is reduced)
when the input is
already nearly sorted.
@BiancaGando

@BiancaGando

Selects the smallest element in an array, pushes it into a new array
[1, 6, 8, 2, 5]
[]
Selection Sort
@BiancaGando

Text
Selection Sort

@BiancaGando

Selects the largest element in an array, swaps it to the end of the array
[1, 6, 8, 2, 5]
Selection Sort
(in place)
@BiancaGando

Selects the first element in an array, pushes it into a new array. As each new element is added, insert the new element in the correct order
[1, 6, 8, 2, 5]
[]
Insertion Sort
@BiancaGando

Insertion Sort

@BiancaGando

Selects the first element in an array, considers that our sorted list of size 1. As each new element is added, insert the new element in the correct order by swapping in-place.
[1, 6, 8, 2, 5]
Insertion Sort (in place)
Exercise Time!
@BiancaGando

@BiancaGando

Divide and Conquer
Sorting Algorithms
Part 1: Merge Sort
@BiancaGando

Recursive calls to a subset of the problem
Steps for Divide & Conquer:
0. Recognize base case
1. Divide: break problem down during each call
2. Conquer: do work on each subset
3. Combine: solutions
Divide & Conquer
@BiancaGando

The merge step takes two sorted lists and merges them into 1 sorted list.
Concept: Merging Lists
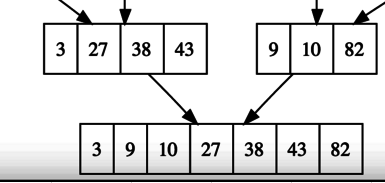
9
10
27
38
43
82
3
X
X
X
X
X
X
X
@BiancaGando

Pseudocode: Merge Routine
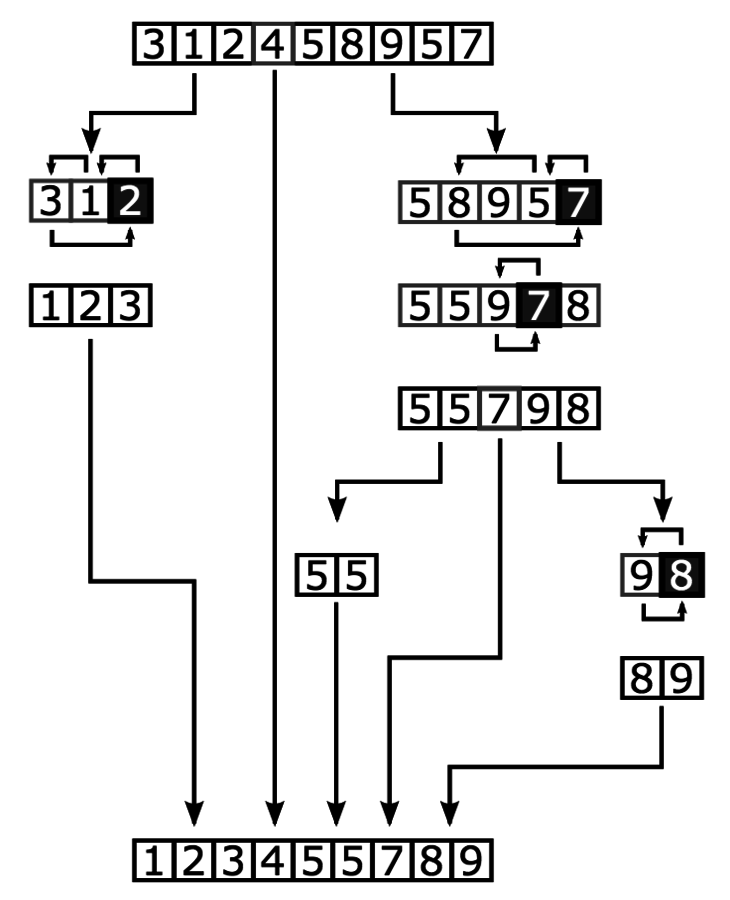
merge(L,R)Concept: Merge Sort
Step 1:
Divide input array into 'n' single element subarrays
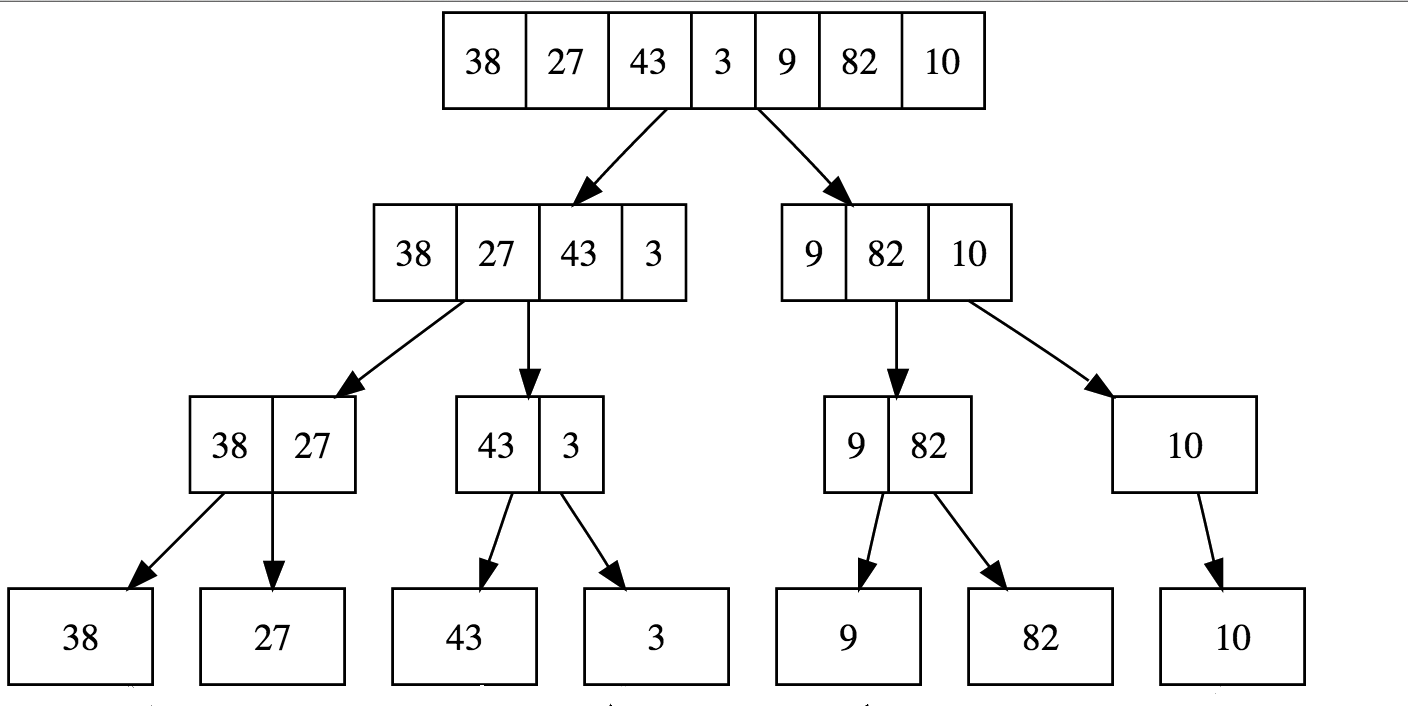
@BiancaGando

Step 2:
Repeatedly merge subarrays and sort on each merge
Concept: Merge Sort
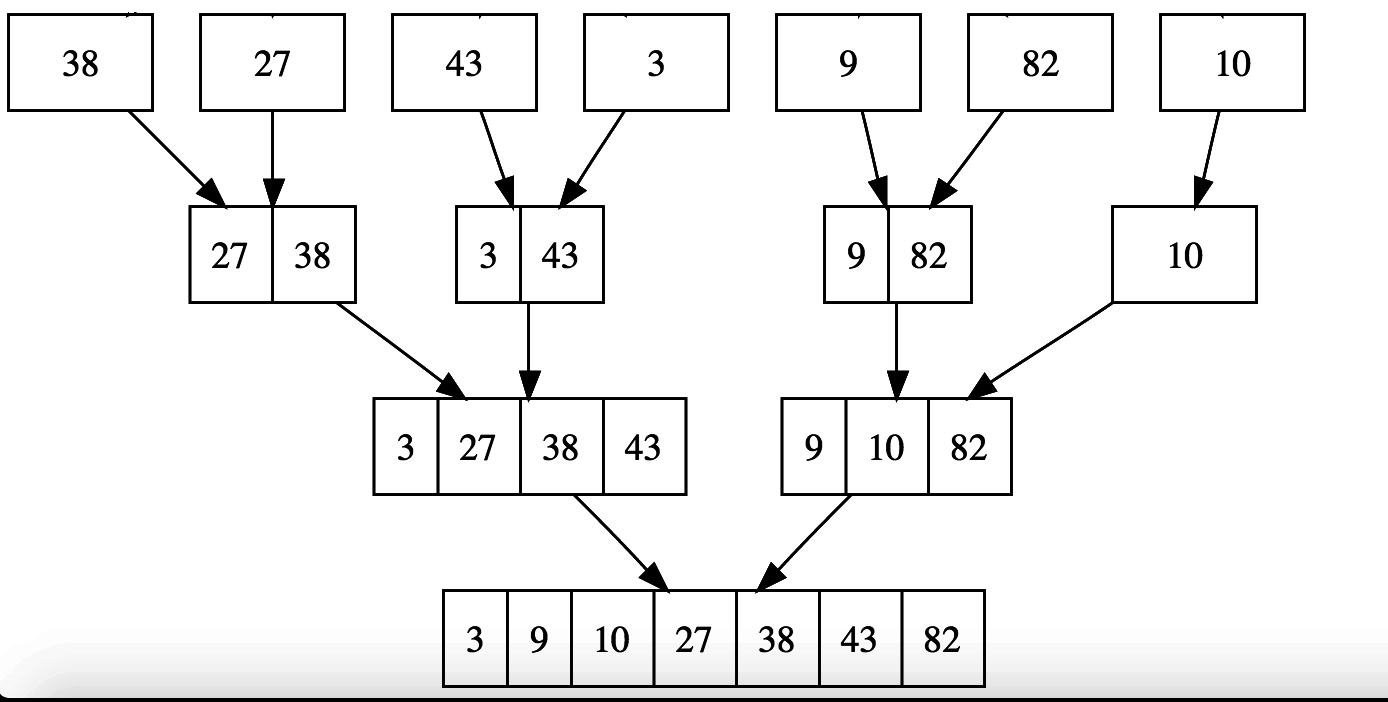
@BiancaGando

Concept: Merge Sort
interactive visualizations here
https://www.youtube.com/watch?v=XaqR3G_NVoo
@BiancaGando

@BiancaGando

Pseudocode: Merge Sort
mergeSort(list)
base case: if list.length < 2, return
break the list into halves L & R
Lsorted = mergeSort(L)
Rsorted = mergeSort(R)
return merge(Lsorted, Rsorted)
@BiancaGando

Pseudocode: Merge Sort
mergeSort(list)
initialize n to the length of the list
base case is if n < 2, just return
initialize mid to n/2
left = left slice of array to mid - 1
right = right slice of array mid to n - 1
mergeSort(left)
mergeSort(right)
merge(left, right)
@BiancaGando

Analysis: Merge Sort
mergeSort(list)
initialize n to the length of the list
base case is if n < 2, just return
initialize mid to n/2
left = left slice of array to mid - 1
right = right slice of array mid to n - 1
mergeSort(left)
mergeSort(right)
merge(left, right, a)


constant
N/A
linear

n/2
f(n) = c1 + n + 2(n/2) + c2
= O(n*logn)
@BiancaGando

O(n*logn)
Time Complexity
Array O(n)
Space Complexity
Exercise Time!
@BiancaGando

@BiancaGando

Divide and Conquer
Sorting Algorithms
Part 2: Quick Sort
@BiancaGando

Recursive calls to a subset of the problem
Steps for Divide & Conquer:
0. Recognize base case
1. Divide: break problem down during each call
2. Conquer: do work on each subset
3. Combine: none
Divide & Conquer
@BiancaGando

In merge sort, the divide step does little, and the hard work happens in the combine step. Quicksort is the opposite: all the work is in the divide step.
The process in which we select our pivot and rearrange all the elements that are greater than, to the right and all the elements that are less than or equal to on the left.
Concept: Partition
Concept: Quick Sort
Step 1:
Pick an element to act as the pivot point in the array

@BiancaGando

Step 2:
Partition the array by reorganizing elements
Concept: Quick Sort
Values less than the pivot come before the partition, values greater go afterwards
@BiancaGando

Concept: Quick Sort
Step 3:
Recursively apply steps 1 and 2 to the subarrays on either side of the pivot
@BiancaGando

Diagram: Quicksort
@BiancaGando

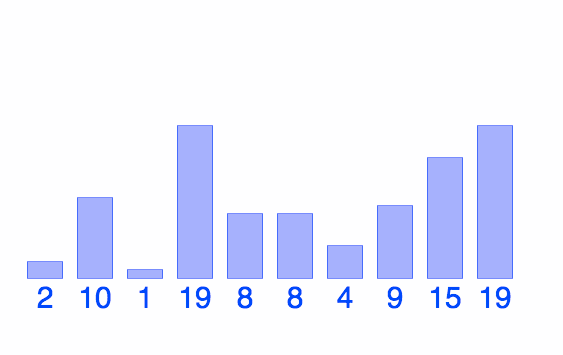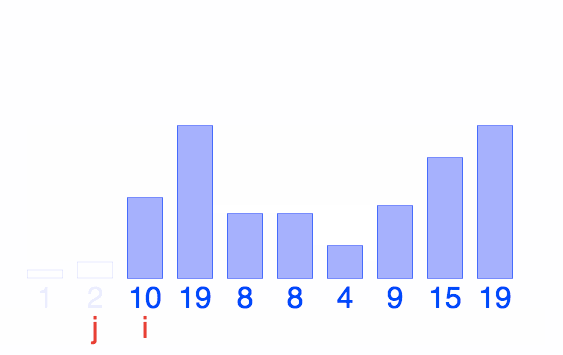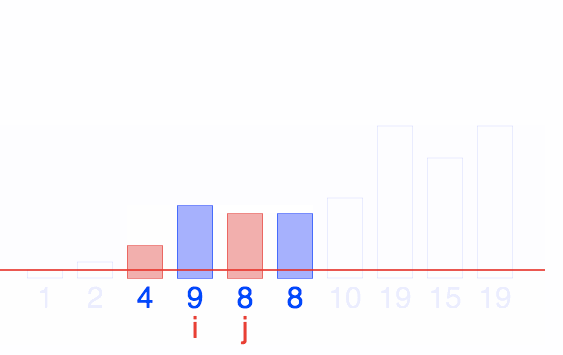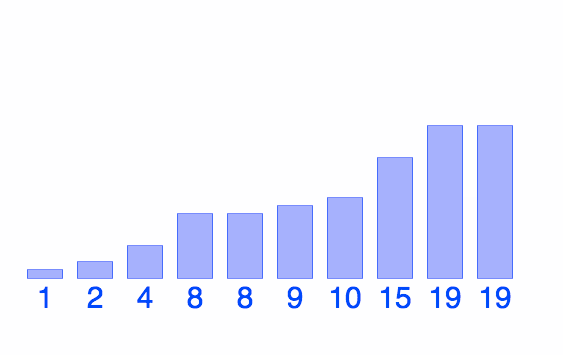
interactive visualizations here
https://www.youtube.com/watch?v=ywWBy6J5gz8
@BiancaGando

Many ways to implement the partition step
Vocab
Pivot point: The element that will eventually be put into the proper index
Pivot location: The pointer that keeps track of where the list is less than on the left and greater than our pivot point on the right. Eventually becomes equal to pivot point when sorted.
Detail: Partition
@BiancaGando

Goal:
Move the pivot to its sorted place in the array
Steps:
1. Choose pivot point, last element
2. Start pivot location at the beginning of the array
2. Iterate through array and if element <= pivot, swap element before pivot location
Detail: Partition
@BiancaGando

Pseudocode: Quick Sort
partition(arr, lo, hi)
choose last element as pivot
keep track of index for pivotLoc
initialized as lo
for i, loop from low to high
if current arr[i] <= pivot
swap pivotLoc and i
increment pivotLoc@BiancaGando

Pseudocode: Quick Sort
quickSort(arr, lo, hi)
first call lo = 0, hi = arr.length -1
if lo < hi
partition
sort subarrays L & R
@BiancaGando

O(n^2)
Time Complexity
O(n)
Space Complexity
Why do we use quick sort when merge sort is the same? That's because the constant factor hidden in the math for quicksort causes quicksort to outperform merge sort.
@BiancaGando

Unstable
Not Adaptable
Characteristics: Quick Sort
Exercise Time!
@BiancaGando

